基于ARIMA-GRNN组合模型的汽车零部件需求预测研究

耿立校，张永杰（河北工业大学 经济管理学院，天津 300130）

0 引言

迄今为止，汽车零部件企业进行需求预测主要还是以传统的时间序列预测为主，其中自回归移动平均模型（ARIMA）就是当中最具代表性的时间序列预测法，该模型可以对任何数据建立时间序列进行分析和预测[1]，因此ARIMA模型被广泛应用于股价预测、人口预测、流行疾病预测、企业需求预测等[2]。由于市场具有很大的波动性从而导致时间序列具有大量非线性特征，传统时间序列预测法在处理线性时间序列拥有独特的优势，但是无法解释时间序列中非线性时间序列信息。伴随人工智能的发展与兴起使得各种先进算法被大量的使用在非线性数据处理，先进算法处理非线性数据可以极大提升预测精度。国内学者胡宁静和陈宏针对网络流量的时变形和非线性指出运用单一的预测方法较难精准预测网络流量[3]。另外，彭连会和张祥波构建ARIMA-RBF组合模型充分利用ARIMA的先进拟合算法功能与RBF非线性拟合算法功能，对重庆市月度降雨量进行实际预测，结果表明ARIMA-RBF组合预测模型是一种优越的算法[4]。

文章构建ARIMA-GRNN组合预测模型来精准处理时间序列集中的线性序列与非线性序列，并利用无锡博世公司CRIN3-18型号产品2016～2018年产品每月实际销售数据进行仿真和测试，将两种模型的预测结果进行比较，验证组合预测模型精确度与可靠性。

1 背景知识

1.1ARIMA模型

ARIMA模型全称差分自回归移动平均模型，是将非平稳时间序列经过d阶差分处理转化为平稳时间序列，然后将因变量仅对它的滞后值以及随机误差的现值和滞后值进行回归所建立的模型。

假设有一组样本时间序列Zt｛｝弱平稳数据，经过d阶差分处理转化为：

所以ARIMA模型的可以表示为：

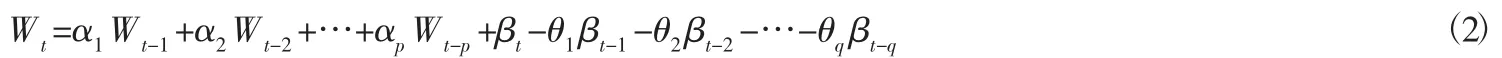
上式中：B是后移算子且BkZt=Zt-k；▽是差分符号且▽=1-B；t是第t时刻的时间点；Zt是第t时刻的时间序列值，βt是均值为0且方差为σa的白噪声。

1.2 RBF神经网络模型

RBF神经网络是由一个具有径向基函数神经元的隐层和一个具有线性神经元的输出层构成的两层向前神经网络[5]。RBF函数神经元的传递函数最常用高斯函数作为神经元的传递函数，神经元radbas的输入是向量p和权值向量w之间的距离与阀值b之间的乘积。泛化回归神经网络GRNN是由一个径向基网络层和一个特殊的线性网络层0组成，常用于函数逼近[5]。

2ARIMA-BP组合模型构建

假设原始时间序列Zt｛｝由线性时间序列Pt｛｝和非线性时间序列Qt｛｝构成即：

ARIMA-BP组合模型预测步骤：

Step1：ARIMA模型对原始时间序列｛Zt｝进行预测结果为原始时间序列｝与预测时间序列之间的误差假设为｛Dt｝，误差序列｛Dt｝中则隐藏着原始时间序列｛Zt｝的非线性关系。式（4） 中F为非线性函数，ωt随机误差。

Step2：利用径向基神经网络强大的非线性函数逼近功能，对误差序列｛Dt｝实现函数逼近。假设误差序列｛Dt｝的预测序列为｛D't｝。

3 实例仿真

仿真数据来源于无锡博世公司CRIN3-18型号产品2016年1月至2018年12月每月实际销售数据（仿真数据以作保密处理）如图1所示。

3.1 ARIMA模型预测

2016年1月至2018年12月一共有36组原始时间序列可视化后如图1所示。图1显示出3年内每个月产品需求量的波动较大，原始时间序列是非平稳时间序列需要利用差分处理使原始时间序列趋于平稳。原始时间序列1阶差分处理后如图2所示。

图1 原始时间序列图

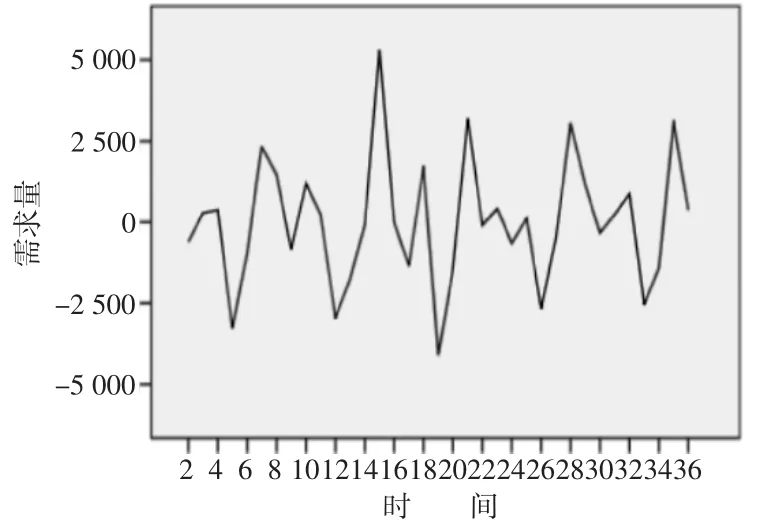
图2 原始时间序列1阶差分图

原始时间序列经过1阶差分处理均匀分布在0刻度线附近，可以视为差分后的时间序列趋于平稳所以d取值为1。1阶差分时间序列的自相关和偏自相关图如图3和图4所示，经过试验对比p取8、q取1时AIC和BIC取得最小值分别为615.96和633.38。

Ljung-Box检验对残差序列检验其Prob值均大于0.05，残差序列不存在自相关性，而且QQ图检验（如图5）所示结果表明基本符合正态分布，最后对进行原始时间序列进行预测，如图6所示。

3.2 GRNN神经网络误差值预测

由于ARIMA预测结果与实际值之间存在较大的误差，根据第二步利用泛化回归神经网络（GRNN）进行对误差序列实现函数逼近，仿真结果如图7所示。

图3 1阶差分自相关图

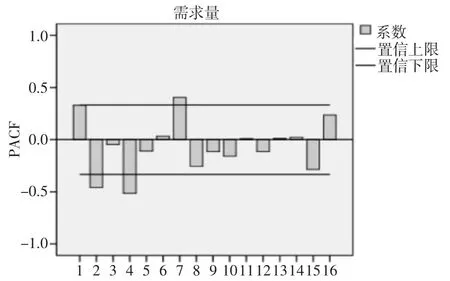
图4 1阶差分偏自相关图

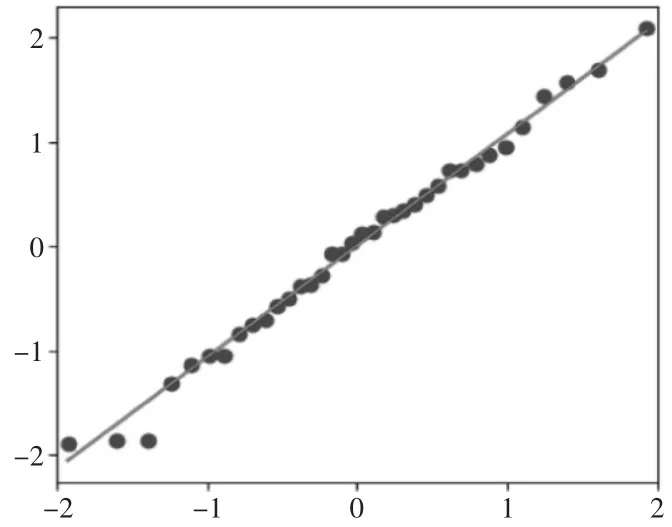
图5 正态度分布检测图

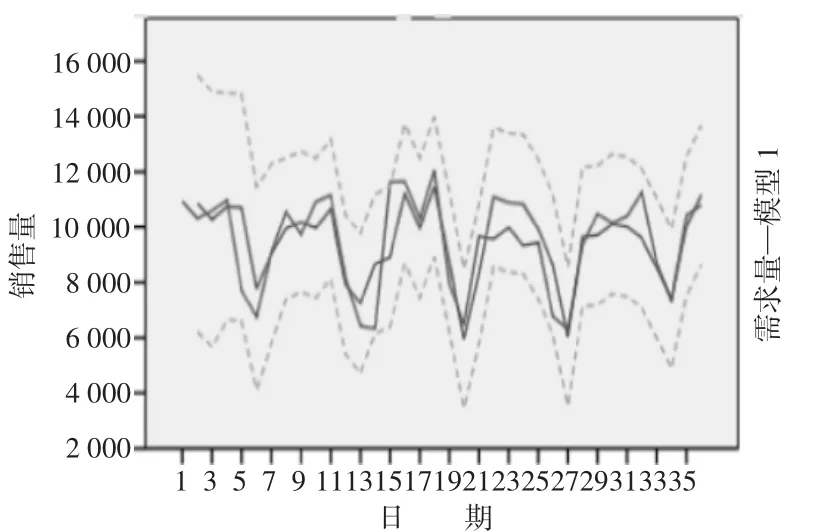
图6 ARIMA（ 8,1, ）1模型预测结果

3.3ARIMA-GRNN组合模型预测

根据第三步将ARIMA（ 8,1,1 ）对原始时间序列预测值与GRNN神经网络对误差预测值相加的值就是ARIMA-GRNN组合模型的预测值，如图8所示。

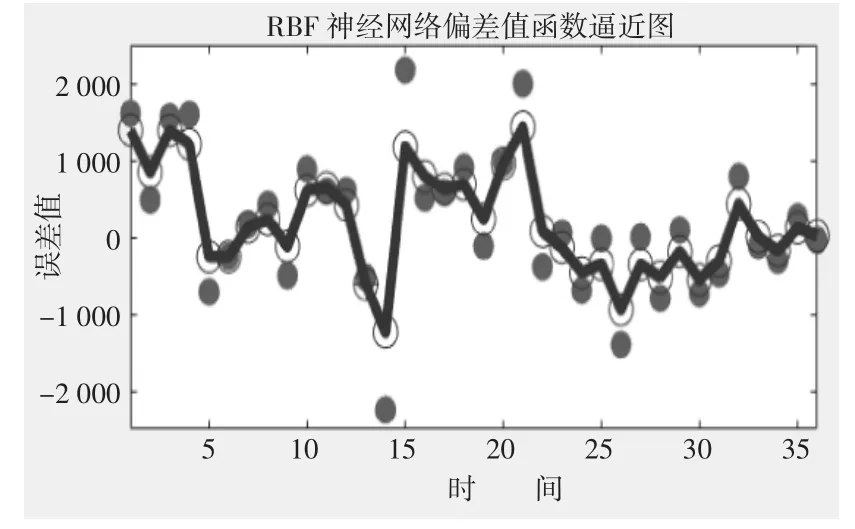
图7 GRNN神经网络误差值函数逼近图

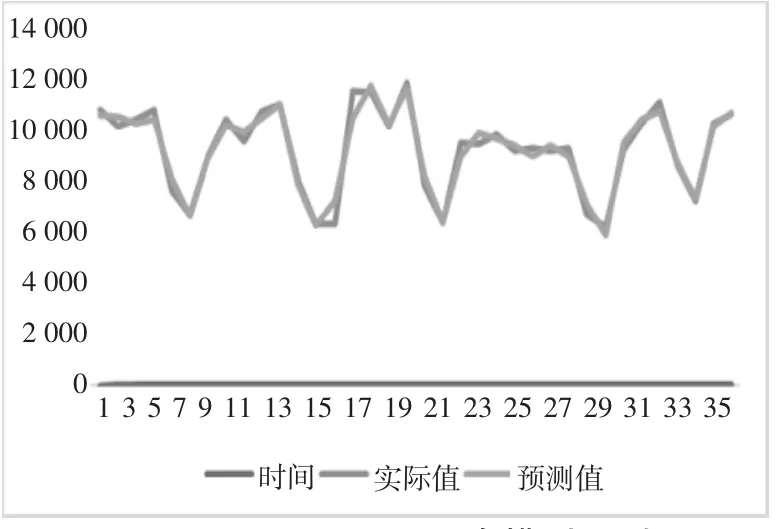
图8 ARIMA-GRNN组合模型预测图

3.4 性能评估

最后通过RMSE和MAPE对两种模型评价，其中ARIMA模型的均方根误差值为0.093、平均绝对误差值为7.771，ARIMA-GRNN组合模型均方根误差值为0.036平均绝对误差值为3.085。综合上述：ARIMA-GRNN组合模型的预测精度明显优于ARIMA模型，且预测结果科学可靠。

4 结束语

本文利用ARIMA模型处理线性数据和GRNN神经网络处理非线性数据各自特点，将两种模型进行组合充分发挥出两者的优点。试验表明ARIMA-GRNN组合模型的预测精度明显优于单一模型，而且精确度更加科学可靠。对于在智能制造模式下帮助汽车零部件企业提高需求预测精度具有一定的帮助与提升意义。