学习进阶视角下小学生统计思维发展水平研究

李化侠

学习进阶视角下小学生统计思维发展水平研究

李化侠

（人民教育出版社 课程教材研究所，北京 100081）

统计思维是数据素养的支撑，是大数据时代公民的重要素养．学习进阶能够描述学生思维发展的轨迹，使用该方式研究学生统计思维发展水平及特点，可以为学生学习、教师教学、教材编写提供参考．使用基于学习进阶理论编制的“小学生统计思维测评试题”，调查了13所学校的2 332名四~六年级学生．研究发现：小学生统计思维的发展总体呈上升趋势，主要处在过渡化、数量化特征水平，还达不到分析水平；不同年级的学生发展速度不同，五~六年级的学生发展速度快；不同维度的发展速度和发展水平不同，数据阅读与表示维度发展速度快、发展水平高，数据分析维度发展速度缓、发展水平低；不同内容的发展水平不同，读取、描述、制作直观统计图发展水平高，数据不确定性、平均数、根据数据预测和判断的发展水平低．

统计思维；数据分析；学习进阶；思维发展水平；多维等值

1 问题提出

“统计与概率”被认为是数学新课程中小学教师最“头疼”的一项内容，这一领域思维方式独特，教师难教、学生难学[1]．实证研究表明，小学生基本不会分析数据，受过训练的初中生能运用一些简单的统计量分析数据[2]，但统计推理中存在依赖主观、曲解题意、忽视平均数受极端值的影响等错误[3]，面对实际统计问题时应用意识薄弱[4]，即使到了高中阶段，高中生应用直觉推理和错误概念的现象也较为普遍[5]，不能有效地对统计论断进行批判性思维[6]．然而，大数据时代数据分析素养是数学核心素养[7]、公民的核心素养[8]．统计素养是课程连接的纽带，促进学生理解统计概念、运用统计知识进行问题解决、熟练自如地运用统计知识进行统计推理等一般能力的发展，还能增强学生的数量能力、网络信息技术能力、批判/创新思维、个体与社会能力、跨文化理解能力[9]．

信息社会背景下，引导学生培育扎实的数据分析素养、形成良好的统计思维是数学教育的时代需要．但事实上，中国基础教育阶段的统计教育实践及研究都较为薄弱．在CNKI的“期刊”“学位论文”中分别以主题为“统计观念”“数据分析观念”“数据分析能力”“统计素养”“统计思维”“统计推理”“统计能力”“统计认知”为条件进行搜索，时间限定到2019年8月15日，共检索到论文218篇，其中期刊论文180篇，学位论文38篇．期刊论文中20.5%来自《小学数学教育》，6%来自《小学教学参考》，学位论文中只有3篇博士学位论文．当前研究内容主要涉及课程标准解析[10]、教材编写[11-12]、教材的中外比较[13-14]、统计与概率教案和教学方法[15-16]、数据分析观念（统计观念）的发展状况[17-18]、数据分析观念（统计观念）的培养策略[19]等多个方面．归纳这些文献可以发现，核心期刊上论文数量较少，博士学位论文占比较低，实证研究、特别是有关学生统计学习特点及规律的实证研究还不多，中国基础教育阶段统计教育的研究显得较为薄弱．

小学阶段的统计与概率是中国基础教育阶段统计教育的重要构成和其它学段的学习基础，统计思维是统计教育的一个重要目标．小学生统计思维是学生在小学阶段对数据收集、数据整理、数据分析的感性认识和理性思考[8]．学习进阶的定义仍无定论，研究者认为各种不同的定义都聚焦学生在某一学科概念的思维发展历程，描述学生在某一时间内思维发展、思维进步的情况[20]．目前，学习进阶被广泛应用于课程标准修订[21]、教材编写及课程设计中[22-23]．基于学习进阶理论实施小学生统计思维的诊断性测验，能更精准、详细地了解小学生的统计思维发展状况，在宏观及中观层面上可为课程标准修订完善、教材内容安排提供数据支撑，在微观层面上可为发现小学生统计思维发展的优势和不足、搭建学生学习和教师教学“脚手架”提供参考．

从学习进阶的视角来了解小学生统计思维的发展水平和发展规律，试图解决以下问题．（1）小学生统计思维的发展水平如何？（2）小学生统计思维的发展轨迹如何？（3）小学生统计思维发展的难点何在？结合以往的研究成果[24-26]，提出如下研究假设．研究假设1：小学生统计思维发展主要处于特征水平、数量水平阶段，尚难到达分析水平；研究假设2：小学生统计思维并非匀速发展；研究假设3：不同教学条件下，小学生统计思维的发展轨迹存在差别；研究假设4：涉及直观形象思维的小学统计内容，学生发展较好，但需要抽象思维、逻辑推理的内容，学生感觉困难．

2 研究方法

2.1 研究工具

使用“小学生统计思维测评问卷”作为研究工具．以学习进阶的方式进行开发，测评问卷包括28道题目，从数据收集、数据整理、数据分析3个方面测量小学生在个体特征水平（水平1）、过渡水平（水平2）、数量化水平（水平3）、分析水平（水平4）的表现．结合小学阶段学生的统计学习内容，“小学生统计思维测评问卷”各维度的主要内容及水平规定如下．

（1）数据收集．主要表现为学生认识数据来源的能力．其个体特征水平可描述为：纯粹基于主观想法认识和收集数据；过渡水平可描述为：基于日常经验描述和收集数据，选择与调查有关的变量、方法；数量化水平可描述为：能设计简单的调查表，开始考虑调查变量、调查方法；分析水平可描述为：收集数据时考虑样本、随机性及抽样方法．

（2）数据整理．主要表现为学生阅读、表示数据的能力．其特征水平可表述为：依照自己的想法产生个人特征的描述或者图表；过渡水平可表述为：能对数据分组、排序，使用自创的图形或图表表示数据；数量化水平可描述为：能解释分组的意义，知道选用典型的、最多的特征描述数据，建立有效图形；分析水平可描述为：能使用不同的方式进行数据排序，解释排序方法的意义，使用一些统计量描述数据，绘制有效的统计图，且能概括统计图表的内容．

（3）数据分析．主要表现为学生解读、阐释数据的能力．其特征水平可表述为：对呈现的数据没有反应或反应无效，对数据能说明什么没有反应或反应无关；过渡水平可描述为：能够对呈现的数据进行比较，解释数据说明了什么问题，但反应的信息量有限；数量化水平可表述为：能超出当前数据范围区分变量，对数据说明了什么问题做出多种相关反应；分析水平可表述为：能区分从数据间读到的信息和从数据外读到的信息，对数据不能说明什么问题做出全面的、结合背景的反应．

该测评工具的试题类型包括填空题、传统多项选择题、顺序多项选择题、主观题，信度、效度良好，克隆巴赫系数为0.908[27]．

2.2 研究对象

选取两个省及直辖市的13所学校的2 332名四~六年级学生作为研究对象．研究对象选取时充分考虑样本的代表性和典型性：13所学校既有来自东部沿海省份的学校，也有来自西部地区的学校；既有来自贫困山区的村小，也有经济较为富裕地区的村小；既有来自贫困地区的乡镇小学，也有经济相对发达地区的乡镇小学；既考虑到经济、教育发展状况一般城市的教学质量好、中、差的学校，也考虑到经济、教育状况较好城市的重点小学，以及城乡结合部的学校及农民工子女学校．

调查样本中城市学校的学生为1 273人，占54.6%，农村1 059人，占45.4%．男生1 209人，占51.8%，女生1 100人，占47.2%（注：个别学生未填写性别，有缺失）；四年级学生795人，占比34.1%，五年级学生781人，占比33.5%，六年级756人，占比42.4%．

2.3 数据采集

数据收集采用了以班级为单位的整群抽样，在13个学校的四~六3个年级各抽两个班．选取这种抽样方法主要考虑抽样便捷性及学习进阶理论纵向追踪的研究需求．由于实际研究中收集纵向数据困难，研究假定“同一学校中不同年级学生的发展具有连续性”，采用这种抽样方式是为了达到以比较各年级学生思维的差异来刻画学生统计思维的发展轨迹的研究目的．

数据获取有两种方式：一种是研究者及助手深入班级实施调查，并深度访谈；另一种是委托小学校长、班主任代为调查，通过详细的操作手册，说明调查目的、要求、时间、方法及注意事项，确保施测流程标准、数据真实有效．

问卷按学习进阶对应的水平赋值，填空题和传统多项选择题采用0、1计分，顺序多项选择题和主观题采用多步计分，按照题目的测量水平依次标定为0、1、2、3．

2.4 数据处理

数据处理使用了R软件、SPSS 20.0．处理分两步：（1）计算量尺分数．先使用R软件中的包估计出学生统计思维能力总分、分维度的似真值[28]，再各随机选取一组，运用=500+100的标准分转换公式，将似真值转换为量尺分．（2）换算等值分数．固定四年级学生的题目参数，采用极大似然估计（Maximum Likelihood Estimate，MLE），使用多维等值技术分别估计五年级、六年级学生统计思维能力的总分、分维度得分．等值处理的目的是便于不同年级、不同维度的分数能够直接比较．

3 研究结果

3.1 小学生统计思维的发展水平

借助项目反应理论的能力参数与题目参数处在同一量尺，并可以互相转换的优良特性，使用了难度指标衡量小学生统计思维发展水平．根据项目反应理论的性质，题目难度能够反应学生的能力：题目难度高，学生作答差，能力水平低；题目难度低，学生作答佳，能力水平高．四年级、五年级、六年级学生在4个水平上的难度参数如表1所示．

表1 四~六年级学生4个水平测试题目的难度

分析表1，可以看到学生在4个水平题目上的表现存在显著差异．水平1的题目，3个年级的学生掌握起来都没有难度；水平2的题目，绝大多数五年级学生可以掌握（=0.25），六年级学生掌握起来显得容易（=-0.30）；水平3的题目有少部分四年级学生能掌握（=0.75），约一半的五年级学生能掌握（=0.50），六年级学生基本能掌握（=0.01）；水平4的题目，3个年级的学生掌握起来都有困难，绝大多数四年级学生无法掌握，六年级学生能掌握的比例也达不到一半．五~六年级学生在水平2、水平3上的难度反应值均位于[-0.5, 0.5]区间，可以推测小学五~六年级很可能是学生统计思维发展从第2水平到第3水平的过渡时期，五~六年级应是学生在水平3的题目上从“较难掌握”到“能够掌握”的发展时期．该研究结果与研究假设1基本相符．

3.2 小学生统计思维的变化轨迹

3.2.1 4个水平的变化轨迹

图1表示的是3个年级的学生在不同水平的题目上的难度．从折线斜率的绝对值看，五~六年级段大于四~五年级段，这说明，小学五~六年级期间统计思维的发展速度高于四~五年级期间．这种变化在水平2（难度变化值0.55）、水平4（难度变化值0.77）上表现得更为明显．

图1 四~六年级学生4个水平测试题目的平均难度

3.2.2 3个维度的变化轨迹

为了更好地呈现学生在各个年级的思维发展速度，研究者比较了3个年级的学生在3个维度上的发展变化．图2呈现了采用多维等值后3个年级的学生的标准分．通过图2可见，五~六年级学生统计思维能力的发展速度高于四~五年级学生，在数据阅读与表示维度上表现最明显．不同年级之间不同的进步幅度验证了研究假设2的观点．

图2 四~六年级学生小学统计思维三维能力

3.2.3 不同学校的变化轨迹

为了进一步验证学生统计思维发展轨迹的不一致性，研究者分析了13所教学条件不一的学校的学生统计思维的变化状况，得到图3．分析图3可见，学校2、学校8的学生在四~五年级时发展缓慢，五~六年级迅速发展；学校5的学生发展速度比较均匀．学校4的学生四~五年级迅速发展，五~六年级发展缓慢．与之不同的是学校3，五年级学生统计思维的得分不增反降．学校8的学生四年级统计思维得分显著低于其他学校，但五~六年级时学生统计思维能力发展迅速，六年级时与其他学校不再有显著差异．可见，不同教学条件的学校学生统计思维的发展轨迹不同，研究假设3成立．

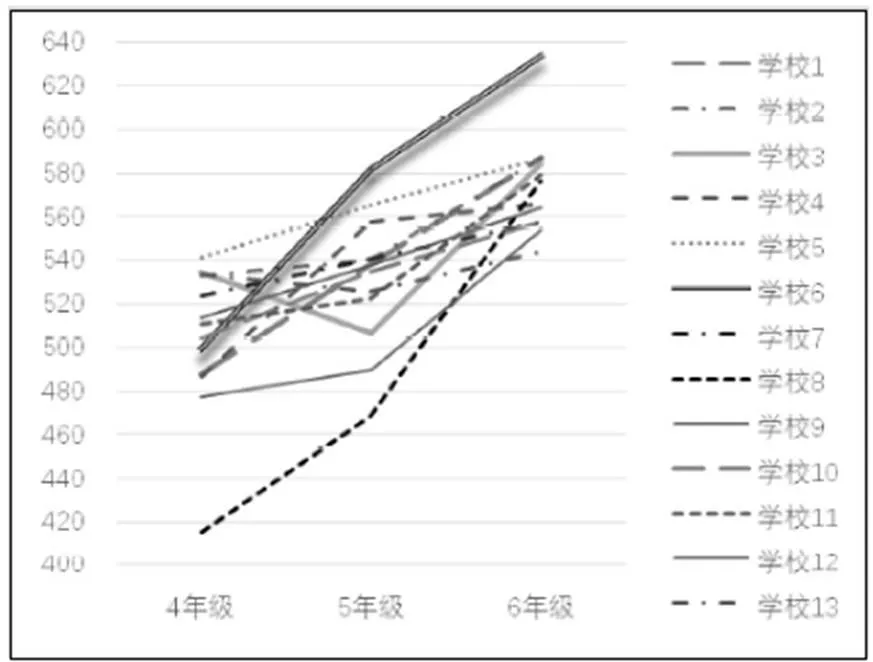
图3 不同学校四~六年级学生统计思维发展特点

3.3 小学生统计思维发展的难点

3.3.1 难点维度

图4是3个维度4个水平的题目的难度均值．分析图4可知，数据描述与表征维度难度最低，即对四~六年级学生而言，数据整理的难度不算大．数据的基本认识维度上，在水平1、水平2，学生尚可凭借朴素经验，但到水平3难度骤增，这与学生未能理解统计数据的变异特征有关．数据分析维度上，总体难度最高，从水平1到水平2、水平3到水平4难度值变化较大，这说明小学生在初步接受数据分析这个领域时感到困难，难以胜任较高水平的数据分析要求．特别需要指出的是，在数据描述与表征、数据分析两个维度上，水平2到水平3的难度变化相对较缓，还出现了水平2的题目难度大于水平3难度的情况，这说明儿童可能在刚刚接触到统计这一领域的内容时感觉困难，但在接触过学习内容后会感觉难度降低，统计学习入门难．

图4 四~六年级学生不同维度不同水平的试题难度均值

3.3.2 难点知识

为了深入分析学生在不同知识内容下的反应，依据测查的内容将测试题目划分为数据阅读与表示、数据收集、数据不确定性、平均数、利用数据解释和预测5部分．采用多维Rasch模型估计学生的作答反应，生成图5．分析图5可见，学生在数据阅读与表示内容上表现较好，在数据不确定性方面表现不佳，在平均数的理解上变异程度较大且总体上表现较差，在根据数据做出解释、预测和判断上，学生的得分表现变异程度较小但普遍得分不高．这表明，四~六年级学生在与统计图表有关的数据阅读与呈现上难度不大，而在理解平均数、数据不确定性、根据数据做出预测和判断上存在困难．

图5 四~六年级学生在不同测试内容的能力状况

3.3.3 难点思维类型

题目的线索数量影响统计思维的表现．学生在单线索的题目上作答反应较好，但增加其它线索，表现变差．学生阅读一般的统计图较容易，如从“饼形图中找出销量最好的口味的蛋糕”这道题目，学生只需要从直观的饼形图中找出占面积最大的部分即可，虽然被调查的四年级小学生并未在课本、课堂中正式学习过饼形图，但96%的学生回答正确．再如，超过90%的被调查者能从折线图中找到最大值、最小值，而被调查中有三分之二的学生并未在课堂中正式学习过折线统计图，六年级的课本才出现折线统计图的内容．但是，如果加入“数据分析”成分，或要求学生运用从图表中读取的数据进一步计算或推理，学生的表现会明显变差．如，要求学生运用条形图进行数量推理、使用折线图的信息分析水温变化，学生的正确应答率从超过90%下降到70%、50%左右．这说明，试题的复杂程度影响学生的表现．这一发现表明，研究假设4中“涉及直观形象思维的小学统计内容，学生发展较好”仅在一定程度上成立，学生的作答反应与试题所需的思维类型有关，还受试题的线索数量的影响，不能笼统地认为涉及直观形象思维的小学统计内容，学生发展较好．

题目所需的思维加工类型影响学生统计思维的表现．深入分析包括了两条及以上线索的题目，发现：涉及简单的数量大小、多少的比较的题目，学生表现尚可，涉及简单“运算”技能的题目学生表现一般，涉及到推理、推断的题目学生表现最差．进行推理或推断时，学生使用具体物品或图形比使用抽象的统计图表现更佳．涉及抽象推理的内容，小学生普遍感到困难，这一现象与学生在理解平均数、数据变异上存在困难具有高度一致性．这些研究结果表明，研究假设4提到的“需要抽象思维、逻辑推理的内容，学生感觉困难”观点成立．

4 结论与讨论

4.1 小学生统计思维的发展水平

小学四~六年级小学生的统计思维发展水平总体上超越了自我特征水平，主要处在过渡化、数量化水平上，但尚未到达分析水平．

学生统计思维的发展状况的研究结果与已有的研究结论基本一致．根据已有的研究成果，学生思维的发展具有明显的年龄特征．如，皮亚杰认为从出生到两岁是儿童的感觉运动阶段、2~7岁是前运算阶段、7~12岁是具体运算阶段、11~15岁是形式运算阶段，5~6岁的儿童形象思维开始迅速发展，7~12岁的儿童处于从形象思维为主向抽象逻辑思维为主的转型，初中二年级是中学阶段抽象思维发展的关键期，到高中二年级，思维趋向成熟[29]．小学阶段的儿童多数在7~12岁，处在形象思维向逻辑思维转型的时期，在中国四~六年级儿童年龄大多在10~12岁之间，结合SOLO分类体系可知，他们的能力处在多点结构，即具备了中等的能力层次，使用问题线索和多个素材，但尚不能注意到素材之间的相互关系．四~六年级的学生的能力发展已经超越了初级具体运算阶段的单点结构，能够较好地解决对单线索素材的问题，因此水平1的题目表现比较好，而需要抽象思维、逻辑思维能力的题目，由于年龄限制，学生思维发展水平尚不能达到，水平4上表现不佳也在意料之中．从学生所处的年龄阶段看，他们的思维发展水平处于第2水平到第3水平的过渡阶段是合理的．

小学生统计思维发展要特别关注和珍惜学生的“过渡阶段”，该阶段学生较多依据生活经验进行统计判断．如，在根据数据做出预测和推断的问题上，相当一部分学生并非根据统计图表提供的信息而是基于自身的喜好“夏天吃雪糕”、生活的经验“秋天水果成熟”做出旅游决策．又如，对数据不确定性的题目，也有较多同学依据自身经验做出“每天上学的方式相同”“爸爸出差了乘坐公交车”“自行车坏了，就得换乘其它交通工具”的回答．虽然学生的作答反应脱离了题目提供的数据，并不是理想的答案，但统计是基于现实情境的问题，结合现实问题进行思考值得倡导．然而进一步分析学生在数据整理、数据分析维度上的表现，发现中国小学生在数量化水平上的表现好于过渡水平．具体表现为学生结合自身经验和生活常识思考的难度大于依据学过的数学知识进行判断的能力，这可能与教师提供了较为直接的教学引导有关，也可能与学生缺少探究、反思有关，学生作答中的观点“没学过，不知道”“我又不是小明，我怎么知道他的想法？”体现了学生对自身经验的忽略及课本知识的依赖．统计思维具有批判思维的属性和功能[30]，要让学生真正理解和把握统计思维，需要加强过渡水平阶段的教学，鼓励学生多结合生活实际与自身经验思考问题．

4.2 小学生统计思维的变化轨迹

小学生统计思维的发展呈总体上升趋势，五~六年级的学生发展速度较快，但不同教学条件下的轨迹并不完全相同．

由于年龄增长理解能力变强、所学知识不断深入，小学生统计思维的发展理应呈现出上升趋势．五~六年级发展速度高于四~五年级，这可能与统计学习的“入门难”有关，也充分说明有些统计知识必须要经过学习才能掌握[2，31]．小学生统计思维发展轨迹的差异，反应出中国教育中普遍存在的一些问题，如东西部教育的差异问题、教育的城乡差异问题[32]，但小学统计思维发展轨迹的调查研究也新发现东部省份一些农村学校的学生统计思维发展水平好于城市学生的特点．深入分析后发现，这与教师的年龄结构、知识结构存在密切关系：由于政策和福利原因，一些年轻教师被安排到乡镇或农村“锻炼”，难以进入“有编制”的城市学校，城市学校中35岁以上的数学教师占比较高，而中国统计教育的内容从2001年课程改革后才进入中小学教材，因此，非数学专业毕业的、35岁以上的小学数学教师，很少学习过统计与概率知识，统计素养不高．再加上各类测评中统计与概率所占分值较少，这部分教师便忽略了完善该内容的知识结构．在调查中，有的数学教师还是学校有一定声望的级部主任，看过测试题之后认为，“选择题没有固定的正确答案，就是看学生怎样思考”，这反应出他们的统计知识比较匮乏．要想提高大数据时代学生的统计思维水平，加强对教师统计内容专业知识的培训，完善其知识结构十分紧迫．

4.3 小学生统计思维发展的难点

学生可以依据生活经验进行朴素的数据收集，但具体到调查表设计、考虑样本代表等较为复杂的内容时，学生反应难度较大．数据整理方面，直观统计图的读取、描述、制作对学生来说难度不大，特别是单线索统计图，即使课本内容未正式接触，多数学生也能够正确作答，但需要两条以上线索、需要推理的统计图，学生的表现会下降．数据分析维度各个水平的题目对学生而言都有较大难度．具体到知识点上，小学生在数据的不确定性、理解平均数及预测和推断数据方面存在较大困难．

数据描述、组织和简化数据、数据呈现3个基本的过程都对学生的数据分析起作用，“目前来看，数据分析是统计思维中最复杂的环节”[33]．数据分析和解释的能力建立在数据阅读、组织和简化的基础之上[34]．数据分析涉及到推理能力、抽象思维能力等方面的能力，而直观统计图阅读、数据描述学生学习起来相对容易，有形象物体的推断也比抽象的推断更容易，这些特点符合儿童认知发展理论7~12岁的儿童处于从形象思维为主向抽象逻辑思维为主的转型[35]的研究结论．小学生数据分析能力发展速度慢、发展水平低，数据阅读与呈现能力发展速度快、发展水平高的特点，提醒小学数学教师在课堂教学中，要注重学生的年龄特点和思维发展阶段，注意教学时间的安排，将学生从直观形象思维阶段逐渐引向抽象逻辑阶段，使学生真正理解统计的实质．

[1] 巩子坤，宋乃庆．“统计与概率”的教学：反思与建议[J]．人民教育，2006（21）：24-27．

[2] 巴桑卓玛．中小学生对统计的认知水平研究[D]．长春：东北师范大学，2006：I．

[3] 何卫国．12~15岁儿童的统计推理认知发展研究[D]．杭州：杭州师范大学，2013：6．

[4] 曲元海．中学生常用统计量理解水平的调查及教学实验研究[D]．贵阳：贵州师范大学，2004：22．

[5] 游敬敬．高中生统计概念学习的研究[D]．北京：首都师范大学，2006：31．

[6] 马萍．山东省某重点高中高一学生统计素养状况的调查研究[D]．上海：华东师范大学，2009：II．

[7] 中华人民共和国教育部．普通高中数学课程标准（2017年版）[M]．北京：人民教育出版社，2018：7．

[8] 李化侠，宋乃庆，杨涛．大数据视域下小学统计思维的内涵与表现及其价值[J]．数学教育学报，2017，26（1）：51-57．

[9] WATSON J. Professor’s page statistical literacy: Connectivity for the Australian curriculum [J]. Australian Primary Mathematics Classroom, 2011 (3): 18-20.

[10] 史宁中，张丹，赵迪．“数据分析观念”的内涵及教学建议——数学教育热点问题系列访谈之五[J]．课程·教材·教法，2008，28（6）：40-44．

[11] 刘福林．小学数学新教材“统计与概率”编写与实验调查研究[D]．重庆：西南师范大学，2004：1．

[12] 孙露．人教版与苏教版小学数学教科书中统计内容比较——基于“统计思维”的视角[J]．课程教学研究，2019（7）：50-59．

[13] 刘曌，杨光伟，唐恒钧．中日两国小学数学课程统计与概率的比较研究[J]．数学教育学报，2013，22（3）：63-66．

[14] 张楠．中美义务教育数学课程标准“统计与概率”领域的比较研究[J]．数学教育学报，2014，23（1）：88-91．

[15] 陈静．了解特点，掌握方法，发展数据分析观念——“折线统计图”内容分析与教学思考[J]．小学数学教育，2019（6）：38-41．

[16] 卢清荣．在对比中培养学生数据分析观念——俞正强“折线统计图”教学片段赏析[J]．江西教育，2016（8）：59-61．

[17] 王艳林．高中生统计思维水平调查研究[D]．南昌：江西师范大学，2016：1．

[18] 欧阳玮媛．高中生统计思维水平发展状况研究[D]．漳州：闽南师范大学，2019：1．

[19] 梁召．小学高年段学生数据分析能力的培养研究[D]．南京：南京师范大学，2018：1．

[20] 高一珠，陈孚，辛涛，等．心理测量学模型在学习进阶中的应用：理论、途径和突破[J]．心理科学进展，2017（25）：1 623-1 630．

[21]  ALICIA C A，翟小铭．学习进阶：描述学生思维发展的有效方式[J]．物理教师，2015（11）：73-76．

[22]  DUNCAN R G, HMELO-SILVER C E. Learning progressions: Aligning curriculum, instruction, and assessment [J]. Journal of Research in Science Teaching, 2009 (6): 606-609.

[23]  DUSCHL R, MAENG S, SEZEN A. Learning progressions and teaching sequences: A review and analysis [J]. Studies in Science Education, 2011 (2): 123-182.

[24]  GRAHAM A J, EDWARD S M. A framework for characterizing children’s statistical thinking [J]. Mathematical Thinking and Learning, 2000 (4): 269-307.

[25]  WATSON J, CALLINGHAM R. Statistical literacy: A complex hierarchy construct [J]. Statistics Education Research Journal, 2003 (2): 3-46.

[26] 彼格斯，科利斯．学习质量评价[M]．北京：人民教育出版社，2010：27-28．

[27] 李化侠，辛涛，宋乃庆．小学生统计思维测评模型构建[J]．教育研究与实验，2018（2）：80-86．

[28]  WU. ACER conquest [M]. Washington: ACER Press, 2017: 65.

[29] 林崇德．思维心理学研究的几点回顾[J]．北京师范大学学报（社会科学版），2006（5）：35-42．

[30]  WILD C, PFANNKUCH M. Statistical thinking in empirical enquiry [J]. International Statistical Review, 1999 (3): 223-248.

[31]  WATSON J M, KELLY B A. Assessment of students’ understanding of variation [J]. Teaching Statistics an International Journal for Teachers, 2007 (3): 80-88.

[32] 袁振国．缩小差距——中国教育政策的重大命题[J]．北京师范大学学报（社会科学版），2005（3）：5-15．

[33]  GROTH R. Development of a high school statistical thinking framework [D]. Champaign: Illinois State University, 2003: 43.

[34]  GRAHAM A J, CAROL A T, CYNTHIA W L, et al. A framework for characterizing children’s statistical thinking [J]. Mathematical Thinking and Learning, 2000 (2): 269-307.

[35] 施羽尧．教育思维学[M]．哈尔滨：黑龙江教育出版社，1990：138．

Developmental Level of the Primary School Students’ Statistical Thinking in Learning Progressions Perspective

LI Hua-xia

(People’s Education Press, Curriculum and Teaching Materials Research Institute, Beijing 100081, China)

Statistical thinking was an important literacy to support data information literacy and citizenship in big data era. Learning progressions was benefit for describing students’ learning trajectory and providing more detailed information for students, teachers and teaching materials. This paper investigated 2 332 primary students who come from 13 schools and study in grade 4 to grade 6 by “test of primary school students’ statistical thinking”, and we found these results: the development of primary students’ statistical thinking showed increase totally, and mainly develops in transition level and quantitative level. Where as the level and speed were different from different grade and different content. The students in grade 5 to grade 6 develop faster than grade 4 to grade 5, reading or representing data develops faster and better than data analysis. And it was hard to understand the data variation, average and data prediction and inference contracts to reading data, describing data, making statistical graphs.

statistical thinking; data analysis; learning progressions; development level of thinking; multidimensional equating

2019–08–20

中国博士后科学基金面上资助项目——学习兴趣测评模型构建及其在小学数学教材编写中的应用（2018M641404）

李化侠（1980—），女，山东莱芜人，副研究员，主要从事教育测量与评价研究．

G622

A

1004–9894（2019）06–0055–06

李化侠．学习进阶视角下小学生统计思维发展水平研究[J]．数学教育学报，2019，28（6）：55-60．

[责任编校：周学智、张楠]