主要作物产量分离方法比较
2020-01-15李心怡赵艳霞杜子璇杨沈斌
李心怡 张 祎 赵艳霞* 杜子璇 杨沈斌
1)(南京信息工程大学气象灾害预报预警与评估协同创新中心/南京信息工程大学应用气象学院, 南京 210044)
2)(中国气象科学研究院, 北京 100081)
3)(河南省气象科学研究所, 郑州 450003)
引 言
农业生产与气象条件息息相关,作物产量和质量易受气候变化与气象灾害的影响。在全球气候变化背景下,地球升温或提前达到1.5℃[1-2],气候变暖导致气候异常和极端天气增多,将对全球作物产生重要影响,从而威胁粮食安全[3-5]。我国气象灾害频发,受灾面积大,成灾比例高,是导致粮食产量下降的主要因素[6-7]。众多学者在农业气象灾害监测预警、气象灾害风险评估、作物产量预报等领域做了大量工作,探究气象与作物生长之间关系[8-12]。作物产量是反映气象条件、品种改良、技术进步等方面的综合表现,在作物产量气象预报业务中,通常将作物实际产量分离成气象产量和趋势产量。气象产量是气象条件变化造成的短期产量波动,趋势产量则是由社会经济、市场供需、技术水平等因素造成的长周期产量变化。将历史作物产量序列进行合理、准确地分解,是研究气象因子对作物产量影响的重要环节之一。
目前,常用的作物产量分离方法包括滑动平均法、指数平滑法、Logistic拟合法和Hodrick-Prescott(HP)滤波法等[13-18]。罗梦森等[13]建立水稻气象产量预报模型时,采用直线滑动平均法确定趋势产量。Iizumi等[14]和Nguyen-Huy等[15]在研究气候对作物产量影响时均采用5年滑动平均法拟合趋势产量。王培娟等[16]在建立冀、鲁、豫三省冬小麦气象产量模型时选取了三次多项式法拟合趋势产量。但大部分研究只选用单一的产量分离方法,选取依据未做过多考虑,评判标准更偏向主观化。
近年来,人们对不同作物产量分离方法进行探讨。房世波[19]以气候变化对棉花产量影响为例,基于趋势产量模拟曲线符合社会技术各发展阶段的实际、气象条件相似区域气象产量应具有很强的相关性以及关键气候因子与棉花生育特性关系的合理性,对三点滑动平均法、五点滑动平均法和二次曲线法进行探讨。牛浩等[20]以山东省玉米为例,运用相关分析与方差分析对HP滤波法、5年滑动平均法、回归分析法和双指数平滑法4种方法拟合趋势产量的显著性和分离气象产量的准确性进行比较。赵东妮等[21]以辽宁省水稻为例,通过比较各站点趋势产量序列与实际产量的拟合程度以及与区域农业生产力技术发展水平和气象产量一致性,评价了HP滤波法、指数平滑法及Logistic方法的合理性。这些研究侧重趋势产量拟合的准确度以及不同方法分离的气象产量的差异,较少探究分离出的气象产量能否有效捕获气象因子对产量影响。然而,在农业气象研究中,作物产量分离最终目的是获取导致产量波动的气象信息。
因此,本文以江苏省水稻产量为例,统计1985—2018年24个县(市)水稻产量,采用3年滑动平均、5年滑动平均、五点二次平滑、二次指数平滑和HP滤波5种方法,获取趋势产量并用一致性相关系数评价拟合效果。在此基础上,采用年际增量法分离气象产量,并以相对气象产量表示。通过比较6种方法获得的相对气象产量的平均值与标准差初步筛选合适的方法,根据典型年份增减产记录与相对气象产量对比,优选出能准确捕获到气象因子导致产量变异的方法,并利用多元逐步回归建立气象产量模型,进一步分析气象产量与气象因子的关系是否符合水稻的生育特性及其对气候的响应规律,找到最优作物产量分离方法。
1 研究区域与方法
1.1 数据来源
1985—2018年江苏省24个县(市)的水稻产量数据来自江苏省农村统计年鉴,逐日气象数据来自国家气象信息中心,包括日平均气温、日最高气温、日最低气温、降水量、日照时数等,24个气象站点分布见图1。参照该区域水稻常年生长发育期,将逐日气象数据分别处理到旬和月尺度,得到逐旬和逐月最高气温、最低气温、平均气温、降水量和日照时数。1987—2016年气象因子对产量影响明显的记录,来自《中国气象灾害大典》(江苏卷)[22]和江苏省气象局。
图1 研究区域及气象站点分布
1.2 作物产量分离方法
为了研究气象因子与水稻产量之间的关系,首先要剔除历史时期生产力发展水平下的长周期产量分量,得到水稻气象产量。长周期趋势产量一般由社会经济、生产技术等因素导致[23-24]。任一产量时间序列均可分解为趋势产量、气象产量和随机产量,随机产量又被称为随机噪声。因此,水稻实际产量Y可分解为趋势产量Yt、气象产量Yw和随机产量ε,即
Y=Yt+Yw+ε。
(1)
趋势产量Yt可通过3年滑动平均法、5年滑动平均法、五点二次平滑法、二次指数平滑法和HP滤波法5种方法分别拟合获得。
1.2.1 滑动平均法
线性滑动平均是趋势拟合技术最基础最常用的方法[25],相当于低通滤波。用邻近年份的数据平均值表示变化趋势。经过滑动平均后,产量序列中短于滑动长度的周期被削弱。由于本文使用了30年数据,而政策变化、农业产业结构调整等一般都不低于3年,故滑动长度k取3和5,分别做3年滑动平均和5年滑动平均。滑动平均法的缺陷是造成产量序列两端的损失,n个数据只能得到n-k+1个平滑值。为了弥补数据两端的损失,处理时延长时间序列,选取1985—2018年的产量数据进行滑动平均,以保证拟合出的1987—2016年30年的趋势产量数据完整。
1.2.2 五点二次平滑法
五点二次平滑法与线性滑动平均作用一样,对经过一次滑动平均产生的序列再进行滑动平均,得到变化趋势[26],常用于分析气候变化的趋势[27]。对于数据两端的缺失值用上文同样方法处理,扩大时间序列范围,选取1985—2018年的产量数据。
1.2.3 二次指数平滑法
二次指数平滑法是在直线滑动平均的基础上进行改进,用指数序列加权平均。具有计算简单、样本需求量较少、适应性较强、结果较稳定的特点。由于产量序列为30年,初始值可以认定为第1个数据,且产量序列呈明显上升趋势,因此,公式中系数沿用前人研究成果取0.3[28]。因为二次指数法属于叠代,具有滞后性,第1年拟合后的趋势产量数据延用原值,导致分离后的气象产量序列首端缺失。为了弥补缺失,拟合从1986年数据开始,以保证1987—2016年30年的数据完整。
1.2.4 HP滤波法
HP滤波法是Hodrick等[29]提出的用于测算美国第二次世界大战后经济发展的周期趋势项和短期波动项的方法。HP滤波法可看作高通滤波器,将产量的时间序列看作是不同频率成分的叠加,通过高通滤波分离出高频成分(气象产量)与低频成分(趋势产量)。HP滤波法分离出的趋势产量无滞后性,故序列首尾没有缺损。
1.2.5 年际增量法
年际增量法认为影响作物产量波动的诸多因素中,作物品种和肥力影响相对稳定,相邻两年作物产量的变化主要由气象条件变化引起[30]。该方法常用于产量动态预报[31-32]。年际增量法与前文5种方法不同的是,它不对实际产量进行趋势拟合,而是用相邻两年作物单产变化率表述气象因子导致的产量变异。这里引入年际增量法,与其他几种分离方法进行比较。
1.3 相对气象产量
为使气象因子对产量的影响不受时间和地域的限制,采用相对气象产量表征气象产量变异,使不同方法得到的结果具有可比性。定义气象产量与趋势产量的比值为相对气象产量Ya:
(2)
Ya为正值,表示气象因子利于作物生长发育即产量增加;反之,Ya为负值,表示产量减少[33]。
1.4 作物产量分离方法筛选
为比较不同方法捕获关键气象因子或主要农业气象灾害带来产量变异的能力,选取了气象条件对水稻产量影响明显的5个典型年份(表1),其中1997年、1999年、2003年和2007年为典型减产年份,2002年为典型丰产年份。用6种方法得到的相对气象产量与5个典型年份对比,如果与实况一致,则进行记录,5个年份中全部一致则记为100%,有4年一致则记为80%,……,以此类推,选出能捕获到气象因子导致产量变异的方法。

表1 典型年份记录
1.5 作物产量分离方法验证
作物产量分离目的是找到气象因子与作物产量之间的关系。因此,基于选定的作物产量分离方法,采用多元逐步回归法建立相对气象产量与全生育期气象因子的关系模型,模型表达式如下:
Ya=β0+β1x1+β2x2+…+βmxm+e。
(3)
式(3)中,Ya是相对气象产量;x1,x2,…,xm是各气象因子;β0,β1,…,βm为回归系数;e是遵从正态分布N(0,σ2)的随机误差。逐步回归分析显著性采用F检验,引入满足A=0.05的显著因子,剔除A=0.1的不显著因子。用建立的相对气象产量模型对选定的分离方法是否能够合理解释气象因子与产量之间的关系进行合理性检验。
2 结果与分析
2.1 趋势产量拟合
应用3年滑动平均法、5年滑动平均法、五点二次平滑法、二次指数平滑法和HP滤波法5种方法对24个县(市)30年的水稻单产分别进行趋势拟合。结果表明,这5种方法拟合的趋势产量与实际产量均达到0.01显著性水平。以大丰、如皋为例(图2),20世纪80年代由于进一步贯彻执行改革和开放的方针,农民积极性大幅提高;同时生产力的发展,如杂交水稻的推广,农村劳动生产率得到极大提高,生产力持续增长,因此,该阶段粮食产量增长速度较快。而从90年代后期开始,农业种植技术进一步加强,粮食产值稳定增长,但增长速度放缓。由图2可见,5种方法拟合出的趋势产量均能较好反映1987—2016年粮食产量总体增长的特征。
然而,不同方法拟合结果各有特点。HP滤波法拟合的趋势产量表现为平稳向上倾斜,对产量起伏剧烈的部分捕获能力较差。相反,二次指数平滑法保留了产量的波动性特征,拟合出的趋势产量在峰谷处与实际更为接近,如大丰1998—2007年和如皋1997—2003年产量变化。整体上,3年滑动平均、5年滑动平均与五点二次平滑法拟合出的产量趋势较为相似,反映出波动特征,表现为增长趋势上叠加上下起伏。
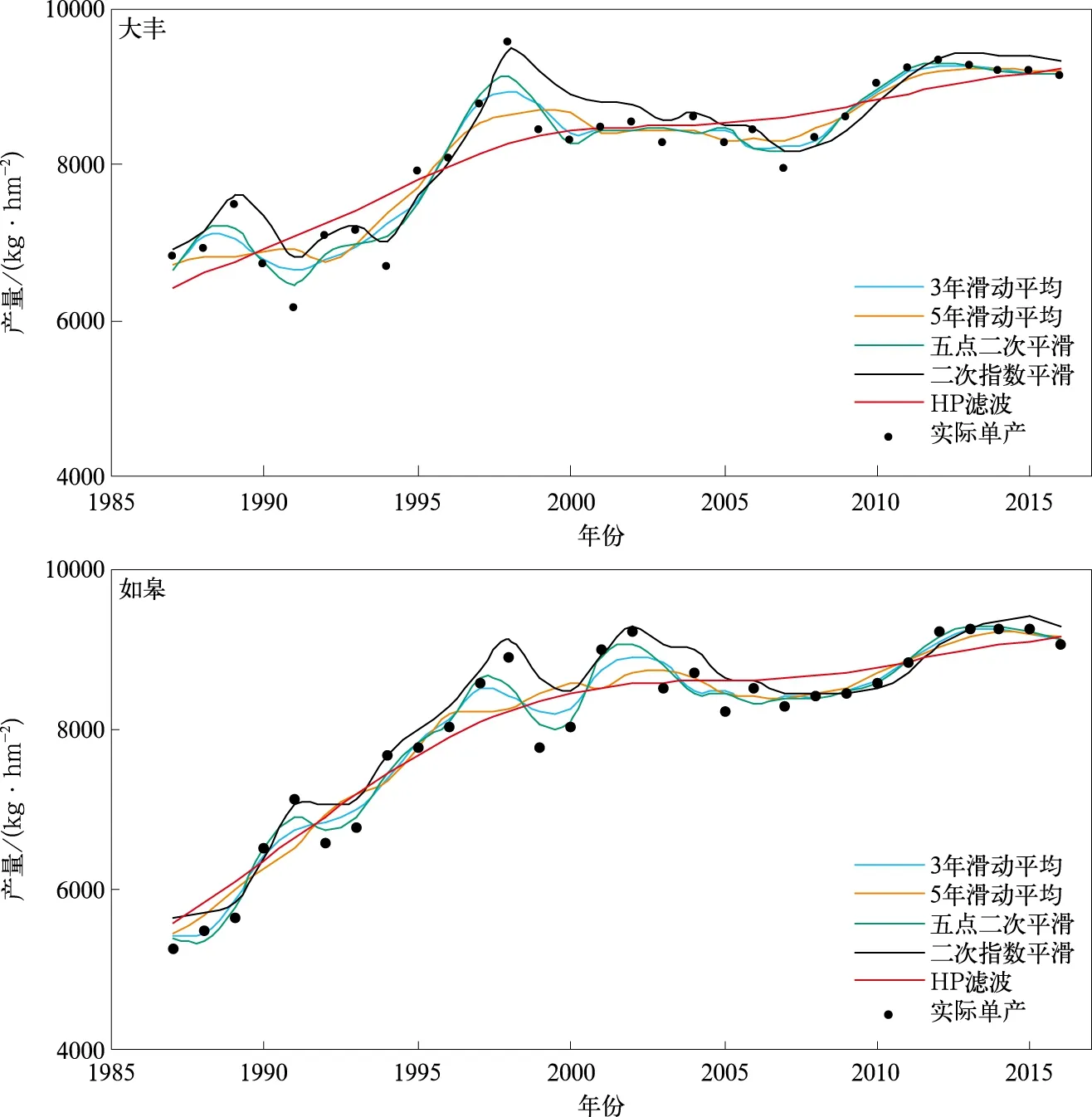
图2 5种方法拟合的1987—2016年趋势产量
由于整个研究区域的社会和技术水平发展过程差异不大,相邻地区趋势产量变化特征应基本一致,因此,用一致性相关系数ρc评价5种方法拟合趋势产量的适用性,当一致性相关系数具有显著性统计学意义时,可结合ρc大小进行一致性程度评价[21]。结果如表2所示,不同方法拟合的各县(市)趋势产量序列与区域平均趋势产量序列均达到0.01显著性水平,基本呈一致性较好和一致性极好,ρc≥0.5;仅极个别地区一致性差,ρc<0.5。由此可见,5种方法均适用于拟合该地区水稻趋势产量。该结论与前人研究结果一致[20-21],即不同产量分离方法在趋势产量拟合上无明显差别。

表2 江苏省24个县(市)不同方法拟合的趋势产量序列与研究区域平均趋势产量序列的一致性检验
2.2 气象产量分离
分别采用3年滑动平均法、5年滑动平均法、五点二次平滑法、二次指数平滑法、HP滤波法以及年际增量法6种方法对1985—2018年24个县(市)水稻单产进行气象产量分离,得到对应的相对气象产量。考虑到同一气候区气候特征相似,且大面积的农业气象灾害发生往往与大的天气过程有关,所以同一气候区或邻近区域水稻的气象产量应具有基本相似的变化特征[19]。因此,以不同作物产量分离方法得到的24个县(市)相对气象产量的平均值作为整个研究区域的相对气象产量序列,并求取其标准差度量随机变量离散程度。合理的产量分离方法得到的不同区域相对气象产量具有同升(增产)同降(减产)的特点,即一致性较好,样本标准差较小;反之,标准差较大[21]。
6种产量分离方法得到的区域相对气象产量的平均值及标准差序列见图3。从平均值看,不同方法的结果具有相似的年际变化特征。具体而言,3年滑动平均法、5年滑动平均法、五点二次平滑法、二次指数平滑法和HP滤波法分离出的相对气象产量结果类似,波动幅度相对较小。年际增量法因只考虑相邻年份的产量变化,因此,波动幅度明显大于其他5种方法,表明年际增量法一定程度上夸大了气象因子对水稻产量的影响。
从标准差看,6种分离方法的标准差平均值从小到大依次为五点二次平滑法(2.4%)、二次指数平滑法(2.6%)、3年滑动平均法(2.8%)、5年滑动平均法(3.4%)、HP滤波法(3.9%)和年际增量法(5.5%),其中,HP滤波法和年际增量法得到的相对气象产量样本标准差序列显著大于其他4种方法,达到0.05显著性水平。结果表明:五点二次平滑法、二次指数平滑法、3年滑动平均法和5年滑动平均法分离得到的各县(市)相对气象产量同相变化特征较明显,HP滤波法次之,年际增量法与其他5种方法差异较大。从研究区域相对气象产量序列反映气象要素年际变化特征看, 五点二次平滑法、二次指数平滑法、3年滑动平均法和5年滑动平均法分离得到的相对气象产量序列更合理。
2.3 作物产量分离方法确定
相对气象产量与典型年记录的比较见表3,6种分离方法捕获整个区域典型年份气象因子或灾害导致产量变化的能力从大到小依次为五点二次平滑法和3年滑动平均法、5年滑动平均法和年际增量法、二次指数平滑法和HP滤波法,且3组间差异达到0.05显著性水平。五点二次平滑法和3年滑动平均法可以捕获绝大多数典型年份气象因子带来的产量变化;其次是5年滑动平均法和年际增量法,能捕获多数典型年份的产量变化;而二次指数平滑法与HP滤波法几乎不能捕获产量变化。
2.2节中的结果已经表明,五点二次平滑法、二次指数平滑法、3年滑动平均法和5年滑动平均法分离的相对气象产量与HP滤波法和年际增量法相比更为合理。其中,五点二次平滑法与3年滑动平均法对于气象产量变异典型年份的捕获能力比二次指数平滑法和3年滑动平均法强。因此,五点二次平滑法和3年滑动平均法有较强的普适性。
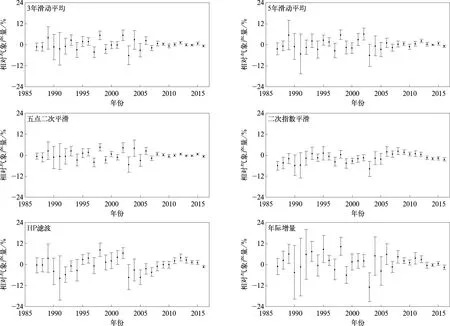
图3 6种产量分离方法得到的相对气象产量区域平均值及标准差序列

表3 江苏省24个县(市)不同方法分离的气象产量与5个典型年记录的比较
2.4 作物产量分离方法的检验
基于以上结果,选用五点二次平滑法与3年滑动平均法建立相对气象产量模型,进一步分析作物产量与气象因子之间的关系是否符合水稻的生育特性及其对气象因子的响应规律。以镇江、金湖为例(表4),回归模型表明,10月上旬日照时数、5月下旬最低气温、6月上旬最高气温、7月上旬降水以及9月降水因子均与水稻相对气象产量呈显著相关,达0.05显著性水平。水稻灌浆-成熟阶段(9-10月),相对气象产量与日照时数为正相关关系,与降水呈负相关关系。该阶段是决定产量的关键期,光照充足有利于水稻光合作用,促进产量形成,阴雨寡照会增加空秕率,使千粒重下降,从而降低产量。此外,强降水可能导致水稻倒伏、受淹,严重影响水稻产量。出苗-分蘖期(5月下旬—7月上旬)的温度和降水都与相对气象产量呈负相关关系。由于江苏省是水稻适宜生长区,温度和降水通常满足该阶段水稻的正常生长发育,但营养生长期温度升高过快,导致作物发育速度加快,生育期缩短,光合作用时间减少,会使水稻减产;同样,该时期降水过多易发生涝渍灾害,不利于水稻分蘖。
因此,3年滑动平均和五点二次平滑法分离得到的相对气象产量能够反映气象因子对产量的影响并可较合理解释相对气象产量与气象因子的关系。
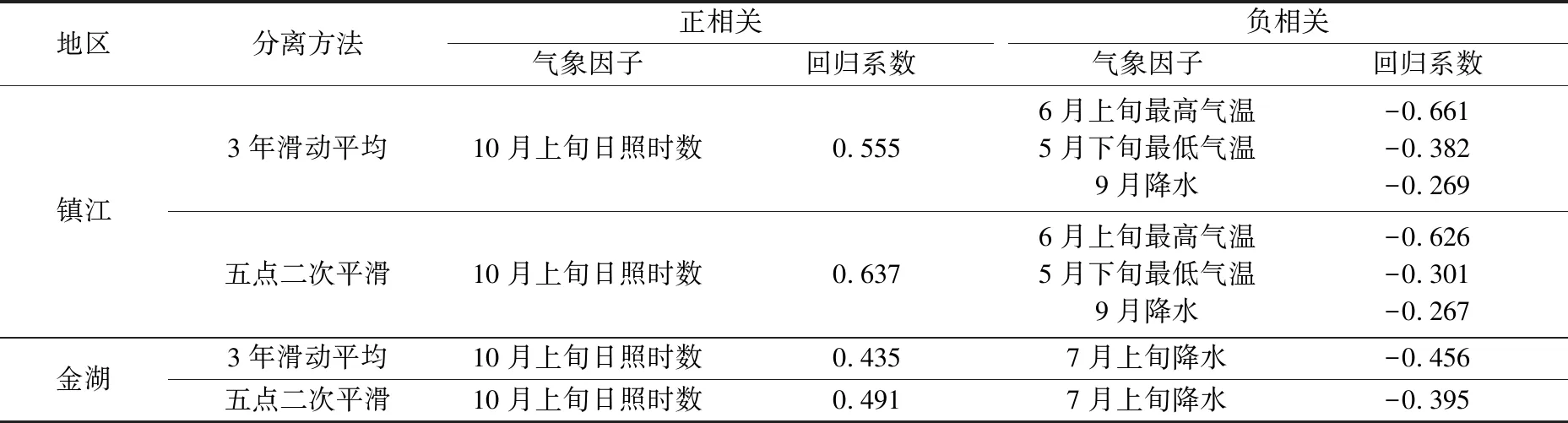
表4 镇江和金湖相对气象产量模型参数
3 结论与讨论
气象条件与作物产量之间的关系一直是农业气象研究的重点。选取合适的方法分离趋势产量与气象产量可准确地描述产量与气象因子的关系,是开展产量预报、气象灾害评估等工作的重要环节。以1985—2018年江苏省24个县(市)水稻历史统计产量为基础,从趋势产量拟合、气象产量分离两方面分析比较了3年滑动平均法、5年滑动平均法、五点二次平滑法、二次指数平滑法、HP滤波法和年际增量法6种方法用于作物产量分离的合理性。首先,将年际增量法与其他5种方法进行比较;其次,将分离出的气象产量与典型年份的增、减产记录进行对比,据此筛选出一致性更高、普适性更强的方法;最后,利用回归模型确定的气象因子与气象产量之间的关系对优选出的方法进行合理性解释。得到以下结论:
1) 从适用性看,3年滑动平均法、5年滑动平均法、五点二次平滑法、二次指数平滑法和HP滤波法这5种方法均适用于水稻趋势产量的拟合,拟合出的产量能表现出随着生产力水平不断提高带来的粮食产量增长的趋势。
2) 从合理性看,通过对相对气象产量序列的均值和标准差的分析,五点二次平滑法、二次指数平滑法、3年滑动平均法和5年滑动平均法这4种方法分离得到的气象产量序列合理性大于HP滤波法和年际增量法。
3) 从普适性看,五点二次平滑法与3年滑动平均法较其余4种方法更具有普适性,基本能够捕获24个县(市)绝大多数典型年份气象因子造成的产量变化。气象产量建模能反映气象因子对产量的影响,符合水稻生长发育状况。
由于我国地域差异显著,气候差异明显,影响产量的要素复杂多样,而且作物产量对技术进步以及气候变化的敏感性不同[34]。在对比作物产量分离方法时未考虑不同长度时间序列以及气候要素突变对产量分离的影响。因此,未来可以考虑通过划分不同时间段选取合适的作物产量分离方法[35]或混合使用多种分离方法得到更准确的分析结果,从而更客观地反映气候变化对作物产量的影响。
