二次函数与相似三角形结合问题的教学探索

周志丽

摘要：最近几年中考题中，二次函数动点与相似三角形结合的问题常出现，引起了初中数学教师的重视，这部分主要涉及数形结合，函数与方程联系紧密，二次函数与相似三角形都是教材的重点和难点，因此，笔者对这两种重要内容的结合就格外重视，突破学生的难点不用盲目搞题海战术，让学生真正掌握解决这类问题的方法和技巧，是笔者近年来执教初四数学重点研究的课题。

关键词：二次函数;相似三角形;教学

中图分类号：G634.6

文献标识码：A

文章编号：2096-3866（2020）16-0162-02

对于“二次函数与相似三角形问题结合”的研究课，笔者通过对此课程的备课设计，并结合多次教学实践、修改教案、课后反思和学生访谈工作，使笔者对此类问题的教学内容层次逐步深化。

一、重视基础，拓展延伸

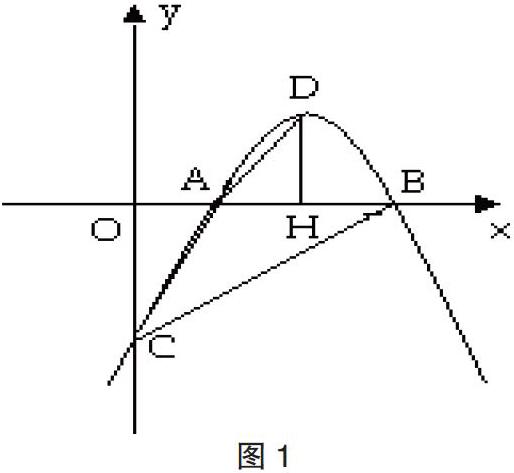
笔者从九年级数学课后习题中找到这样一道题，如图1，已知抛物线y=-（x-2）²+1的图像与x轴交于A、B两点（点A在点B左侧），与y轴交于点C。①试判断△AOC与△COB是否相似;②若点D是抛物线的顶点，DH垂直于x轴，垂足为H，试判断Rt△DHA与Rt△COB是否相似？说明理由。

此题属于相似三角形内容中较基本、较典型常见的题型，笔者对此题的兴趣就始于二次函数的“背景”。于是，在九年级第二轮复习的“相似三角形”的专题课中，笔者把此题作为例题，并进行了变式尝试。

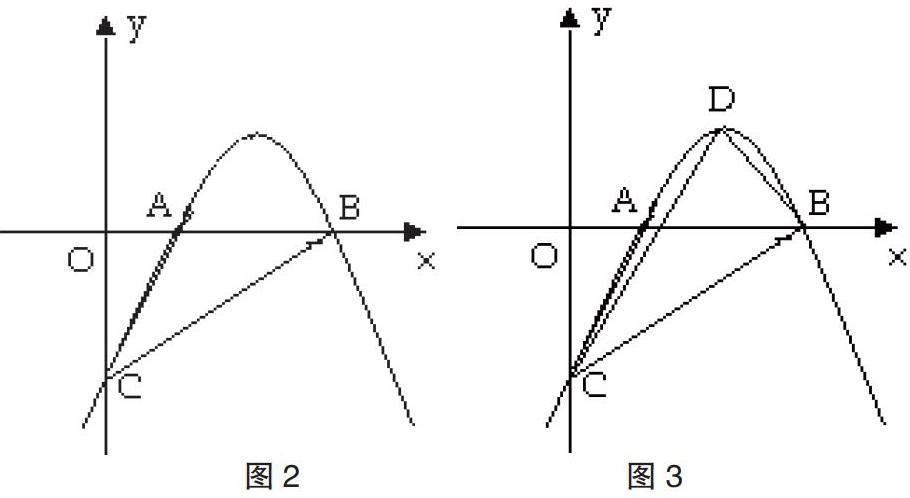
变式一：如图2： y=-（x-2）²+1，若点M在抛物线上且在x轴上方，过点M作MG垂直于x轴，垂足为点G，是否存在M，使得△AMG与△AOC相似。

变式二：如图3：若点D是抛物线的顶点，点M在抛物线上且在x轴上方，过点M做x轴的垂线，垂足为点G，是否存在M，使得△AMG与△DCB相似。

授课时，笔者对此题进行变式主要是想突出二次函数这个背景：一是让学生在“二次函数”这个背景下，通过接触“两个三角形不相似”这种不常见的题型，对两个不相似的已知三角形进行有理由的判断，加深并巩固对相似三角形的判定定理的理解;二是在顶点式这个“二次函数”背景下，给学生提供优化选择解这个一元二次方程方法的平台，在求抛物线与x轴的交点坐标时出现方程-（x-2）²+1=0，在解这个一元二次方程时，可用直接开平方法，也可用因式分解法，当然也可把顶点式化为一般式，再去解所得的一般形式的一元二次方程。显然，如果能用直接开平方法解，可以节约不少时间。

在以上设计思路中可以看出，笔者当时对这节课的认识层次停留在表层，引入背景，只是“为需要背景”而引入背景。虽然想到了要考虑学生的实际，但也只是从具体的知识、具体的方法层面上予以指导。对于九年级的大多数同学来说，此题的综合性不强，缺少在“二次函数”背景下综合应用知识方面的指导。

二、不断演变，提炼本质

课程标准中有“会利用已有的知识经验，自主进行探索和尝试解决新情境中的数学问题”的要求，因此需要加强几何与代数的综合度，让学生能体验、接受基本的数学思想，如数形结合思想、分类讨论思想等。

基于此，再次授课时，为了满足不同层次学生的需求，能把“二次函数”背景下的相似三角形的综合问题能更好的解决，同时，考虑到第二轮复习的需要，笔者又在原题的基础上增加了以下2个小题：

（3）若点M在抛物线上且在x轴上方，过点M作MC垂直于x轴，垂足为点G，是否存在M，使得△AMG与△AOC相似。

（4）若点D是抛物线的顶点，点M在抛物线上且在x轴上方，过点M做x轴的垂线，垂足为点G，是否存在点M，使得△AMG与△DCB相似。

把第（3）题的过程简单说明一下：

本题涉及相似三角形中数形结合、分类讨论问题，很容易分析出已知△AOC的两条直角边的比是1：3，再对△AMG的两条直角边的比两种可能情况MG：AG=1：3或MG：AG=3：1进行分类讨论。第（4）小题，与第（1）小题一样，也是属于一个已知三角形与一个未知三角形的问题，只要学生能分析出△BCD是直角三角形，它的两条直角边的比是1：3，再类比第（1）小题，就可以很顺利地解决第（4）小题。

应该说这种认识层次在原先的表层认识层次上有了较大的提升，既考虑到课程标准的表述，提高了对学生综合能力的要求，又注意到对学生基本的数学思想的要求，同时，兼顾了数学中考的现实要求。

事实上，大部分同学都能想到分类讨论，但学生在具体的解题过程中还是遇到了很大的困难——如何用点M的横坐标和纵坐标来表示两条直角边MG和AG的长。在板书过程中，笔者对“设点M的坐标为（a，-（a-2）²+1）”一带而过，课后学生反映较难理解。由此，可以看出当时笔者的认识层次只能属于中等层次。

三、深度思考，思维提升

通过对讲解后，笔者也进行了反复的思索：笔者已经注意到了学习课程标准，适当提高总复习的综合度，渗透基本的数学思想，为什么不少学生对设点的坐标理解的程度还是不够？基于此，笔者对此课程教学又一新的认识层次要重点，笔者意识到：将书本的语言自如地使用或转换各种形态的数学语言了，才能真正将数学教育理论的符号语言融入到数学教学实践中去了，才能使学生真正理解并自如运用这些数学模型。点的坐标是综合题的立足点（求解析式），又是综合题的制高点（求满足条件的点的坐标或存在性探求），求点的坐标一般历经下面两个关键步骤：（1）定位;（2）计算。因此，探讨如何用点M的横坐标和纵坐标来表示两条直角边MG和AG的长是本题的难点，而解决这个难点的突破口就是先要理解点M的坐标为（a，-（a-2）²+1），于是，笔者在授课中运用了“平面上点的位置与点的坐标”“函数图像上的点与点的坐标满足函数的解析式”等语句。并将此语句运用到新的一次教学过程中，并在黑板上醒目板书：“点的位置——点P（x，y）”、“函数解析式”点在函数图像上-点的坐标满足函数的解析式”，有了前期做的这些铺垫，学生对设点M的坐标为（a，-（a-2）²+1）就很容易理解了。以下在突破难点边AG、边MG等长度时，就迎刃而解了：MG的长即点M的纵坐标的绝对值，而点在x轴的上方，由此可得点M的纵坐标就是边MG的长，而AG的长是点M的横坐标与点A的横坐标的差，在教学中，解决了以上的问题后笔者继续追问：“如果其他条件不变，把‘点M在抛物线上且在x轴上方，直接改为‘点M在抛物线上，该题的解法有没有改变呢？”

这样的变式更凸现了本题的重点，提高了思维的“质”，但关键仍在如何用抛物线上的点M的横坐标与纵坐标来表示边AG、MG的长，当然这时数学语言表示的难度有所加大，数学的能力要求有所提高。

有了这道题目的二次函数“背景”，就有了类比的基础与规范，其他函数图像上的点与三角形结合的问题也一样。一般说来，这类题目都由图像上的点转化到三角形中的边长的问题，再由边的数量关系转化到三角形的相似问题。甚至可以说，函数图像上的点与其他几何图像相结合的问题也一样，由图像上的点转化到几何图形中的边，再由边的数量关系转化几何图形的整体，为了满足一部分数学爱好者或“吃不饱”的学生，更好的关注学生“发展”要求，笔者又进行变式，布置了课后练习，继续深化课堂内容，题目如图4，抛物线y=-x²+bx+c与x轴、y轴分别相交于点A（-1，0）、B（0，3）两点，其顶点为D。（1）求该抛物线的解析式;（2）若该抛物线与x轴的另一个交点为E，求四边形ABDE的面积;（3）△AOB与△BDE是否相似？如果相似，请予以证明;如果不相似，请说明理由。

综上所述，通过二次函数背景下的相似三角形问题的探究学习，学生能体会数形结合和思想、分类讨论思想、相似三角形注意寻找不变的量和相等的量，利用几何定理和性质或代数方法建立方程，在教学过程中通过教师对数学研究的对象数和形之间内在规律的演绎，促使学生学习此类问题有一种“质”的认识，以达到学生学习质量提高的目標，是富有意识的教学实践。