如何利用“数形结合”解决问题

郭双

“数缺形，少直观;形缺数，难入微;数形结合百般好，隔离分家万事休。”这是著名数学家华罗庚先生对数形结合思想的透彻的阐释。

数学中，数和形是两个最主要的研究对象，它们相互转化、相互渗透。数形结合思想，就是在解决问题的过程中，注意把数和形结合起来考察，斟酌问题的具体情形，把图形性质的问题转化为数量关系的问题，利用数量关系突破图形性质的问题;或者把数量关系的问题转化为图形性质的问题，利用图形的性质解决数量关系的问题。利用数与形的相互转化来解决数学问题，使复杂问题简单化，抽象问题具体化，化难为易，获得简单易行的成功方案。

画图，是数学中常用的一种解题策略。小学生年龄小，抽象思维水平不高，而画图比较直观。通过画图能够把一些抽象的数学问题具体化，把一些复杂的问题简单化，容易找到解决问题的关键。所以引导学生采用画图的策略，十分适合小学生的思维特点，也是我最常向学生推荐的一种解题策略。下面谈谈我在教学中采用“数形结合”思想教学的方法。

一、数形结合，激发学习兴趣

画图能把抽象的东西形象化、生动化，学生更能积极主动接受知识，变“被动学”为“主动学”。

例如，我在教学人教版二年级上册《有余数的除法》时，在讲授“余数”这一知识点时学生很难理解，于是教师便给学生提供小棒，用8根、9根、10根、11根、12根小棒摆正方形，可以摆几个正方形，还剩几根？

通过拼摆正方形，学生很容易就得出结论：8根可拼成2个正方形;9根可拼成2个正方形，还剩1根;10根可拼成2个正方形，还剩2根;11根可拼成2个正方形，还剩3根;12根可拼成3个正方形;这里剩下的1根、2根、3根就是“余数”，表示剩余多出来的数。为什么12根小棒摆正方形没有余数呢？通过图形也能很容易得知，11根再添1根，那么余数3根与新添的1根刚好又可以摆成一个正方形，所以没有余数。也可得出结论：余数比除数小。在这个直观的操作过程中，学生轻易突破难点，也大大激发了学生学习数的兴趣，把学生从“被动学”转变成“主动学”。

二、数形结合，形成良好学习习惯

巴金先生说：“孩子成功教育从好习惯培养开始。”在数学解题的过程中要善于培养“画图”的好习惯。“画图”能为学生在解决问题中提供清晰的思路和步骤，形成良好的学习习惯。教师不仅要教会孩子怎样画图，而且要让孩子将“画图”形成一种解题习惯。

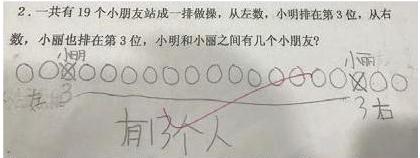
例如，我在教学人教版一年级上册《11-20各数的认识之解决问题》中遇到这类例题：

首先，我会让学生画19个圆圈代表19个小朋友。然后，再找出左边第三个标注“小明”，右边第三个标注“小丽”。为了让学生更清晰的知道小明和小丽不算在内，我让学生把不算的人数打上“×”。最后，用横线画出小明和小丽之间的人数并数出来。

一年级的小朋友对文字的理解有些欠缺，抽象思维水平有限，但通过“画图”把文字意思表述出来就一目了然，学生也容易接受。从小埋下一颗善于画图解决问题的种子，形成一种良好的学习习惯，对于今后的学习有着莫大的帮助。

三、数形结合，激活学生思维

教育大师苏霍姆林斯基说过“孩子的智慧在手指上”。 学生在解决数学问题的过程中利用画图这个中介辅助理解题目，其实他们在画图的过程中就是展示其数学思维过程，闪烁其数学思维火花的过程。学生能把一些看似剪不断、理还乱的数学难题，“翻译”成图表的符号，化繁为简，使问题变得井然有序。整个过程中，学生把文字转成图画，把图画转成思维，是一个从“外化”到“内化”的过程，是一个发展学生逻辑思维的过程。

记得在教学人教版四年级下册《鸡兔同笼》时，书本出示以下例题：

笼子里有若干只鸡和兔，从上面数，有8個头，从下面数，有26只脚。鸡和兔各有几只？

在数量比较少的情况下，我们可以通过列表格找出答案。但是还不能清晰掌握解题方法，为了让学生更直观、简洁、深刻地理解题意，我采用了画图假设。

假设笼子里全部都是鸡，那么就有8×2=16只脚，这样就多出了26-16=10只脚。

一只兔比一只鸡多2只脚，也就是10÷2=5只兔。所以笼子里有3只鸡和5只兔。

在这个过程中，学生一看图就可以理解多出来的10只脚是兔子的，一只兔子比鸡多2只脚，所以兔子有5只，鸡有3只。下次做到类似题目都能先假设全部是鸡或者全部是兔的情况，进而进行计算。在教学过程中巧用“画图”，能将教学内容化繁为简，培养学生的抽象思维能力，引导学生在真实鲜明的感性认识中，发展智力因素，可有效地培养他们的抽象思维能力。

四、数形结合，建立数学方法。

教学中利用数形结合，可以启发学生思考，帮助学生不断积累数学活动经验，感受画图解题策略价值，提升数学思想方法，同时让学生根据自己的体验，逐步领悟，用自己的思维方式构建出数学思想方法的体系。

总之，运用数形结合的思想来解决数学问题，可以将很多抽象的东西趣味化，复杂的东西简单化，空洞的东西生动化。教师要培养学生学会用数形结合思想来解决数学问题，引导学生在真实鲜明的感性认识中发展智力，体会“画图”在数学应用中的魅力。