勾股定理四步曲

肖友文

摘要：本文就北师大版八年级数学上册第一单元《勾股定理》的教学，结合学生的学习情况提出了自己的四个方面的教学意见，目的是为了更有效地实施有效教学，进一步激发学生的学习兴趣与热情，充分地发挥勾股定理在教学实践中的多种功能.

关键词：讲故事、找铺垫、重归纳、巧设计、数学思想方法渗透

勾股定理是几何学中的明珠，之所以它充满魅力，是因为千百年来人们对它的证明趋之若骛，其中有著名的数学家，也有业余数学爱好者，有普通的老百姓，也有尊贵的政要权贵，甚至有国家总统.北师大版八年级数学上册第一单元就是学习勾股定理，作为教师如何引导好学生认真顺利地学习有关勾股定理的知识并加以应用，下面就如何实施与开以展教学谈自己的几点思考.

一、讲故事，激发学生的学习兴趣

课前我就与勾股定理有关的故事作一些比较全面的互联网搜索，并进一步进行整理，旨在通过让学生自己来讲故事的形式使他们能更加具体、全面、深刻地了解勾股定理的由来，并激发大家对数学知识的求知欲望与强烈的兴趣爱好.

二、找铺垫，理清新旧知识的联系

在学习勾股定理之前，我试着与学生一起重温以下两个方面的知识，目的是让学生在后面的学习中能更加顺理成章，这也符合建构主义的理论，简单地说来就是任何新知识的获得，都要建立在新旧知识的联系上，不能脱节.

1.复习以前学过的直角三角形的有关知识

①什么叫做直角三角形？答：有一个角是直角的三角形叫做直角三角形;

②直角三角形中三个角有什么关系？答：三个角的和是180°，两个锐角互余;

③直角三角形三条边有什么大小关系？答：有三边关系定理，任意两边之和大于第三边;

④有哪些特殊的直角三角形？答：有等腰直角三角形，还有30°、60°的直角三角形.

2.1-20的平方的运算

平方虽然是乘法的特殊情形，但它却是四则运算之外的对于学生来讲比较陌生的一种运算，其中的原因是学生对平方的概念理解不透，所以造成运算的错误，具体又分三种类型的題目来做.

①计算1-20的平方;

②反过来做这样的填空题，=25，=64等等;

说明：这里面很多学生都会想到，因为有前面的1-20的平方计算做基础，但是存在的问题是几乎所有的学生都漏了相对应的负数，也就是忽略了互为相反数的两个数的平方是相等的这个性质，所以也可以帮助学生复习巩固一下，顺便也可为后一单元学习数的平方根打下基础.

三、重归纳，提高学生的解题能力

题型的归类有助于帮助学生提高思维的条理性与清晰度，帮助学生系统地掌握好应该掌握的知识，并进一步形成自己的知识网络，最终达到形成自己的基本技能.勾股定理的有关题目大致上可以分为以下三种：

1.直接用勾股定理计算

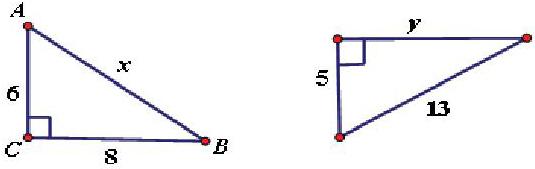
例1：求下列直角三角形中未知边的长度.

分析：象这种题目一定要让学生先观察图形，找出直角边与斜边，然后利用公式写出直角边的平方和等于斜边的平方，即有，从而计算出结果.

2.缺图形

例2：在Rt△ABC中，∠C=90°，AC=6，BC=8，求AB的长.

分析：这一题没有图形，要求学生根据题目的意思画出图形来然后列式进行计算，把图形画出来，就知道与例题1中的第一个图是一样的，所以象这种题目其实是加了一个对数学语言的理解并把它转化成图形.

对应练习：

①、在△ABC中，∠C=90°，若 a=5，b=12，则 c=___________;

②、在△ABC中，∠C=90°，若c=10，a∶ b=3∶4，则SRt△ABC=____________;

③、等腰△ABC的腰长AB=10cm，底BC为16cm，则底边上的高为 ，面积为 .

3.需要设未知数列方程来解决

例3：一个直角三角形的斜边为20cm，且两直角边的长度比为3∶4，求两直角边的长.

分析：未知的有两直角边，也就是说有两个未知数，所以要根据比为3∶4设两直角边分别为3xcm和4xcm，然后用勾股定理列式进行解方程来求解.

解： 设两直角边分别为3xcm和4xcm，

由勾股定理得，

求得，所以两直角边分别为6cm和8cm.

对应练习：一直角三角形的三边分别为a、b、c，其中a=3，b=4，求c的长.

说明：这一题不但考查学生通过读题得出图形的能力，还要求学生注意题目中的细节问题，就是题中没有说明c是不是斜边，所以要分两种情况来解答.

四、巧设计，渗透数学思想方法

日本数学家和数学教育家米山国藏曾经说过这样一段话：学生在中学阶段所学的数学知识，在进入社会后，几乎没有什么机会应用，因而作为知识的数学，通常在出校门不到一两年就忘掉了，然而不管他们从事什么业务工作，那种铭刻于头脑中的数学精神和数学思想方法，却长期地在他们的生活和工作中发挥着重要的作用。是啊，要让学生的头脑充满理性思考，那数学课堂教学的支点在哪里呢？经验是数学的基础，问题是数学的心脏，思考是数学的核心，发展是数学的目标，思想方法是数学的灵魂，勾股定理这一单元里面蕴含着丰富的数学思想方法，只要我们在课堂巧妙地进行设计，于无形中去渗透，方能达到教学的最终的目标.

五、结束语

在教学中我就是按照这样的思路去实施教学，可以说收到了自己意想不到的效果，下面是我教的班里面的部分学生的学习体会：现在我们已经学习了勾股定理，也知道了勾股定理就是说在一个直角三角形中三条边存在一个关系：两直角边的平方和等于斜边的平方，公式就是.用这个定理可以来进行计算，求出直角三角形中未知的一边来，看起来这么简单的一个定理，里面去蕴藏着丰富的故事与数学道理.所以通过这次不同一般的数学课活动，让我们认识到了原来数学课并不是我们以前所想象的那样，只有老师的讲解与同学们的模仿与练习，而是可以有一些那么有趣的活动，比如自己来说故事;还有勾股定理的证明方法让我们也学到了一些令人惊叹的技巧，比如那些数与形结合的思想，让我们感受到数与形结合得那么美妙，这些不仅激发了我们浓厚的学习兴趣与热情，还锻炼了我们的意志与提高了利用网络资源的技能，可谓受益匪浅.