促进深度思维的数学概念教学研究*
2020-01-14韩龙淑刘凯陈锦楠
韩龙淑 刘凯 陈锦楠
摘 要 深度学习是学科核心素养培育的基础和关键,数学深度学习的实质重在深度思维。以典型数学概念为例,从创设疑难情境引发概念学习需求、数学概念的自然导入、数学概念的自然生成、数学概念的变式强化和迁移、数学概念结构网络的构建、数学概念的拓展深化等方面解析促进学生深度思维的数学概念教学路径,提出促进深度思维的数学概念教学启示。
关键词 深度思维 數学概念 疑难情境 自然生长
深度学习是核心素养培育与发展的基本途径[1],是学科核心素养落地生根的关键。而数学是思维为主的科学,数学教学的价值在于思维教学[2],在于启发学生学会数学思考,因此数学深度学习的实质重在深度思维。其中数学深度思维主要体现为数学思维的活跃度、数学思维的含量、数学思维的层次和数学思维的强度,旨在优化思维策略,完善数学思维品质,促进数学深层理解和变式迁移。
《义务教育数学课程标准(2011年版)》指出:数学知识的教学,要注重知识的“生长点”与“延伸点”[3]。研课中发现,学生若缺乏对数学概念产生的必要性和合理性的感悟,未引发学习新概念的情感需求和思维需求,则容易导致数学概念的机械学习或表层学习,因此基于促进深度思维进行数学概念的教学研究具有重要意义。
一、促进深度思维的数学概念教学路径
学源于思,思源于疑。深度思维源于强烈的认知冲突、疑难困惑并生成问题。鉴于目前多数教师对“为什么教学新概念”缺乏足够的认识,致使数学新概念产生的必要性和价值体现不够,未能使学生感悟学习新概念的现实需要和数学自身发展的需要,从而不易形成认知和情感的内在学习需求。因此促进学生深度思维的数学概念教学首先需要研究“为什么学习此概念”,激活学习新概念的情感需求和认知需求(Why);其次需要研究“学习数学概念的哪些内容”(What),挖掘数学概念的本质及生成过程等。要促进学生的深度思维,提升数学思维的活跃度、含量、层次和强度,数学概念应尽量以“概念形成”的方式进行学习,使学生经历概念形成的过程。如表1所示。
1.创设疑难情境提出问题,引发学习新概念的情感需求和思维需求
深度思维源于情境中自然生成的疑难和困惑。通过创设疑难情境、营造知识缺口,引导学生在已有知识和经验基础上激活思维、产生困惑并发现提出问题,引发新概念产生的情感需求和思维需求。
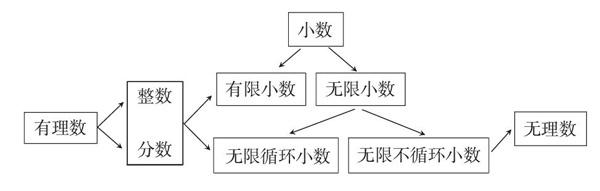
无理数是中学数学核心概念,其发现在数学发展史上经历了艰难曲折的过程,是初中数学教学的难点。课堂观察发现:初中生只知道“无理数是无限不循环小数”,再问什么是无限?什么是不循环?学生往往模棱两可,表现出对无理数概念本质认识的茫然。
问题1:前面我们学习了有理数,有理数包括整数和分数,如果将下列整数或分数写成小数形式,你有哪些发现?
遵循知识的发生发展过程和学生头脑中与新知识有实质性联系的适当观念,启发学生发现有理数可表示为有限小数或无限循环小数,并把有理数的小数表示作为新知识的生长点。
2.感悟数学概念产生的必要性和自然性,提升数学思维的层次和活跃度
以学生认知结构中与新概念有自然的、内在联系的已有知识作为新概念的生长点,使新旧概念之间产生非人为和实质性联系,感悟数学概念导入的自然性和必要性,从而提升数学思维的层次和活跃度。
问题2:是否存在无限不循环的小数呢?圆周率你能写到多少位?教师借助PPT整屏幕展示圆周率的近似值:3.14159265358979323846264……,使学生直观感知圆周率的精确值书写不完,是无限且不循环的小数。
体验无理数产生是数学自身逻辑发展的需要。
问题3:数学发展史上毕达哥拉斯学派的门徒西帕索斯发现边长为1的正方形的对角线不能用整数或整数比表示。而边长为1的正方形的对角线是腰为1的等腰直角三角形的斜边,启发学生自然思考腰为1的等腰直角三角形的斜边长a。借助等腰直角三角形面积的两种不同表征,逻辑推理得到[7]a2=2,斜边的长是多少呢?1 学生感悟到有限小数和无限循环小数不够用了,由于数学自身发展的需要自然会出现无限不循环小数,而不是人为造出的,感悟无限不循环小数存在的自然性和合理性。 无限和不循环理解起来有难度,学生不易建构无理数概念。通过逻辑推理而不是动手操作的拼补图形,探索等腰直角三角形斜边的长,提升了数学思维的层次和活跃度。 3.经历概念抽象概括的自然形成过程,提升数学思维的含量和强度 要促进学生的深度思维,提升数学思维的含量和数学思维的强度,数学概念尽量以“概念形成”的方式进行学习,使学生经历概念获得的辨别-分化-抽象—概括—检验—表示等思维活动过程。 问题4:结合圆周率的值:3.14159265358979323846264……,a2=2时a的值,0.5050005000005...(相邻两个5之间0的个数逐渐加2),启发学生对情境进行辨别和分化,自然抽象概括无理数是无限不循环的小数,或者不能表示成两整数之比的数。 通过三个变式情境启发学生结合有理数概念的经验以及对无理数来源的认识,抽象概括无理数概念的本质,体现数学概念的自然形成过程。 4.通过正反例变式强化,促进数学概念的深层理解和拓展度 促进学生对数学概念的深层次理解,需要通过正反例的变式强化,变更数学概念的非本质属性,突出数学概念的本质特征,并将所学概念灵活迁移到问题解决中,达到数学概念的深层理解和深度迁移。 ①下面各数中哪些是有理数?哪些是无理数? 3.14,-■,0.■,0.1010001000001(相邻两个1之间0的个数逐渐加2), ②(1)假设面积为10的正方形的边长为x,x是否为有理数?说说你的理由 (2)对x的值进行估计(答案精确到0.1),并用计算器或机验证估算结果 (3)如果结果精确到0.01呢? 通过正反例变式强化无理数概念,理解无限不循环小数的本质,并巩固用有理数估算无理数的方法,借助计算机进行检验,与现代信息技术深度融合。 5.构建数学概念网络系统,体验概念自然生长的思维主线和思维方法的关联度 知识经过分类组织具有结构后,才易于理解、迁移和运用。梳理并提炼数学概念自然生长的思维主线和思维方法,通过概念之间的横纵向关联度,构建数学概念网络系统,形成组织良好的概念网络结构。 引导学生构建知识结构体系,建立新旧知识之间的纵横联系,促进对新概念的深度思维和深层理解,旨在形成组织良好的数学认知结构网络。 6.认识数学概念的历史发生过程,感悟数学的理性思维价值和延伸度 呈现数学发展史上无理数产生的艰难曲折历程,并用反证法逻辑推理得到平方为2的数是无理数。通过体味数学新概念产生的历史发生过程和思考方法,对数学概念进行深度加工和拓展深化,使学生感悟数学的理性思维等文化价值,提升数学思维的延伸度。 二、促进深度思维的数学概念教学启示 1.读懂并创造性运用教科书,把握数学概念的本质 一节自然生长且促进深度思维的数学概念课,关键在于深层理解概念并能迁移运用概念。教师在教学设计时,需要深层理解教科书,并对不同版本教科书内容进行精选和整合。 目前有两个以上版本的初中数学教科书中,无理数概念的引入是把两个边长为1的小正方形“剪一剪,拼一拼”,得到一个大正方形,发现面积为2的正方形的边长是无理数。虽然剪和拼也可以产生无理数,但是剪和拼的动手操作和直观感知比较突兀,为什么要通过“剪和拼”得到一个大正方形呢?学生缺乏对无理数概念產生的抽象过程的体验,降低了数学思维的抽象层次。通过启发学生逻辑推理发现腰为1的等腰直角三角形斜边长的平方为2,以此探索平方为2的数的本质特征。既提升了理性思维的层次和思维的强度,又有利于抽象无理数概念的本质,体现概念的生长到思维和智慧的生长。 2.尽可能使学生感悟数学新概念产生的必要性和自然性 通过现实需要的分析,让学生感悟数学与现实及其他学科的联系,产生概念学习的情感需求;通过数学自身发展需要的分析,使学生产生数学概念学习的思维需求。 深度思维重在使学生体验到数学概念等的起源与发展是自然的,是已有数学概念不够用了,是水到渠成和有人情味的,从而经历概念产生过程中的火热数学思考,在头脑中展开高水平的数学思维活动,感悟数学概念产生的必要性、自然性和合理性。教学中需要教师创设疑难、困惑的“愤悱”情境,并运用启发性提示语、合乎情理地引导学生探索数学概念的自然生成,从而使鲜活的数学概念在学生头脑中自然而然地流淌出来。 3.课堂小结重在使学生构建数学概念图,形成组织良好的认知结构网络 课堂小结是数学概念教学的重要环节之一,旨在对所学概念进行梳理归纳、改造重组和系统提升。对强化数学概念、启迪学生深度思维、形成数学概念网络和促进数学迁移具有重要作用。概念教学中教师尽量,引导学生归纳概念的本质和研究方法等,并辅以文字、图表等搭建数学概念网络图。网络的节点越多,通道越丰富,概念理解越深刻,从而形成组织良好的数学概念认知结构网络。以此促进数学深度思维,切实提升数学学科核心素养。 参考文献 [1] 郭华.深度学习与课堂教学改进[J].基础教育课程,2019(02). [2]卜以楼.生长数学:数学教学的理性回归[J].中国数学教育,2017(09). [3] 中华人民共和国教育部.义务教育数学课程标准(2011年版)[S].北京:北京师范大学出版社,2012. [4] 曹才翰,章建跃.数学教育心理学(第3版)[M].北京:北京师范大学出版社,2017. [5] 范芬瑞,韩龙淑.基于PCK视角的数学原理的教学设计—以勾股定理为例[J].天津师范大学学报:基础教育版,2018,19(04). [6] 韩龙淑.数学教材分析中发展应用意识素养的双向路径[J].教学与管理,2018(02). [作者:韩龙淑(1965-),女,山西榆次人,太原师范学院数学系,教授,博士;刘凯(1995-),女,山西交城人,太原师范学院教育学院,硕士生;陈锦楠(1997-),女,天津人,太原师范学院教育学院,硕士生。]【责任编辑 刘永庆】
