基于混沌蜂群算法的USV 路径规划

兰 莹，章 甜

(上海海事大学，上海 201306)

0 引 言

路径规划通常分为两类，一类是全局路径规划，即在已知的环境中，依照距离最短、能耗最低、耗时最短为目标，找到一条避开障碍物的最优路径，全局最优的典型算法包括A*算法、D*算法等。二类是局部路径规划，即事先并不完全知道地图环境，根据当前已探知的信息完成路径选择。近年来，不少学者将全局路径优化算法与智能算法相结合，尤其是新兴智能优化算法的使用。吴丰君[1]提出了基于协作思想的改进粒子群优化算法，郑佳春等[2]提出一种基于混合模拟退火与粒子群优化的无人艇路径规划算法，倪生科等[3]提出一种基于混合遗传算法的船舶避碰路径规划，YUE 等[4]介绍了一种基于蚁群算法的无人小车路径规划算法，王鹏等[5]提出一种混合自适应蚁群算法的AUV 路径规划方法，田屏[6]提出一种基于混沌搜索改进的人工蜂群算法。

人工蜂群算法（ABC）于2005 年由Karaborg 提出，在函数优化方面的效果明显[7]，相比于上述优化算法，人工蜂群算法具有参数设置少、计算简单、收敛快等特点。但同样容易陷入局部最优，本文将基于人工蜂群算法结合Logistics 混沌映射产生雇佣蜂的混合算法，优化USV 作业路径。

1 模型建立

为方便问题分析，对无人艇作以下假设：

1）船载监测设备已探知小船周围障碍物位置；

2）无人艇行驶的环境为二维平面，忽略水面波浪所致小船起伏；

3）忽略障碍物高度，每一个障碍物占据一个二维栅格；

4）无人艇、目标点、障碍物位置均处于栅格中心点；

5）无人艇最大转向角为45°。

而路径规划之前，通常要对无人艇的作业环境进行建模。常见的环境建模法包括顶点图、邻接图、栅格法等，其中最为常见的即栅格法建模，通过栅格将地图环境进行存储，包括起点、终点、障碍点信息。栅格地图的距离计算通常有3 种方式。

1）曼哈顿距离。曼哈顿距离即坐标系中两点的绝对轴距之和，其表达式如下式：

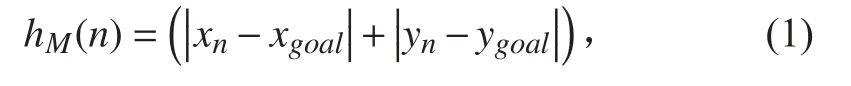
2）切比雪夫距离。切比雪夫距离被称为棋盘距离，其表达式下式：

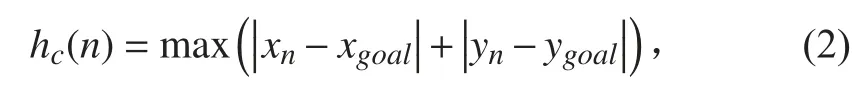
3）欧几里得距离。其值直接可以看作两个位置点在欧式空间中的两点的直线距离，其表达式如下式：

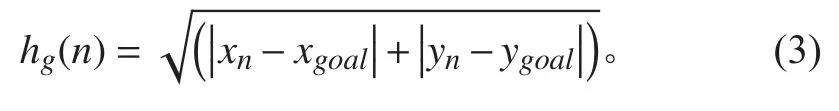
无人艇的最大转向角设定为45°，曼哈顿距离只能支持横向、纵向的移动，故距离计算选择可以斜向行走的切比雪夫距离。

假设无人艇单位时间内移动的距离为R，则根据探测器探测范围距离内的海域按栅格进行等距划分，每一行、每一列的栅格数为：

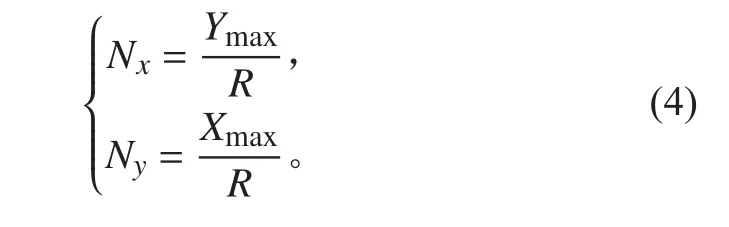
其中：Ymax和Xmax分别为探测范围内的纵向、横向的最远距离。

无人艇路径规划是避免碰撞的前提下，保证路径长度最短，是一个典型的约束最优问题，数学模型描述如下：

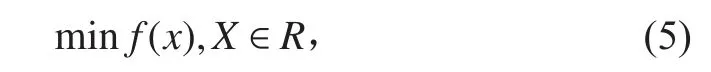
约束条件[8]为 gi( X)≤0,i=1,2,···,p。

对于此类带约束非线性最优化问题，可以将其转化为无约束最优化问题，等价于一个能量优化函数E，其由路径长度函数（Ei）和碰撞惩罚函数（Ec）组成。

含有N 个路径节点的情况，路径长度函数El为所有线段长度之和，即

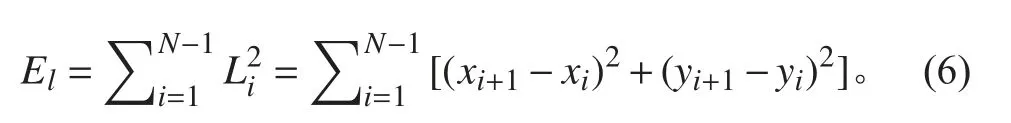
碰撞惩罚函数Ec为无人小船在作业过程中，全部路径节点的碰撞惩罚函数能量之和，即

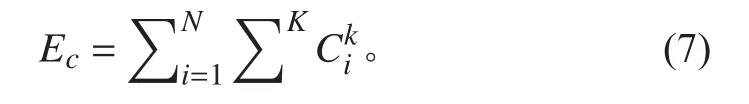
其中权值 μl+ μc=1，目标函数为：

2 蜂群算法与改进

人工蜂群算法（Artificial Bee Colony Algorithm，ABC 算法）是一个由蜂群行为启发的算法，在2005 年由Karaboga 小组为优化代数问题而提出。人工蜂群算法包含3 个基本元素：蜜源、雇佣蜂、侦察蜂[9]。其中蜜源代表问题解空间内的各种可行解，每个解是Xi(1,2···,m)一个D 维向量。雇佣蜂则是用来引领蜂群，并保存蜜源的相关信息，其数量和蜜源数量相等。侦察蜂则需要在蜜源附近随机搜索新的蜜源，选中蜜源后，雇佣蜂继续引领蜂群保存蜜源信息，并留下较优解。循环直至算法结束。

在标准人工蜂群中，蜜源更新位置公式如下：

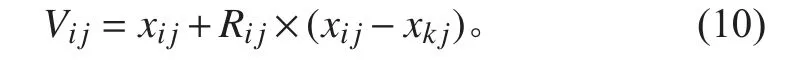
式中： K ∈(1,2···,S N) ，SN 是种群规模，j ∈(1,2···,d)，即随机选取下标。Rij是[-1，1]之间的随机数。

侦察蜂的蜜源选择概率公式：

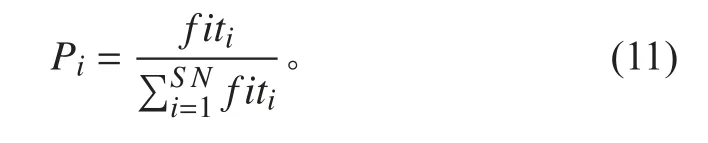
针对传统蜂群算法的不足，本文提出在信息素更新时引入混沌算子，通过混沌序列的全空间遍历和变异操作的特性来增加算法种群多样性，迭代后期则去除混沌扰动避免振荡。

引入混沌序列对随机数序列进行动态调整改进，目的是当一定参数设置下，混沌序列的输出可以呈现完全无序，随机，遍历状态，起源于虫口模型的Logistic 混沌序列在 μ= 4 时（ μ为增长率），系统处于混沌工作状态[10]，公式如下：

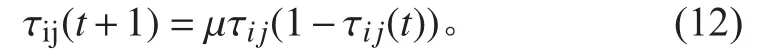
式中： τij(0) 为 初 值， τij(t)指算 法 在 第iter 次迭代时的值，根据混沌理论，当初值 τij(0)不等于0.25，0.5，0.75 时，序列完全处于混沌态，提高搜索多样性。

图1～图4 为处于混沌状态的随机序列和特殊值下的混沌序列。

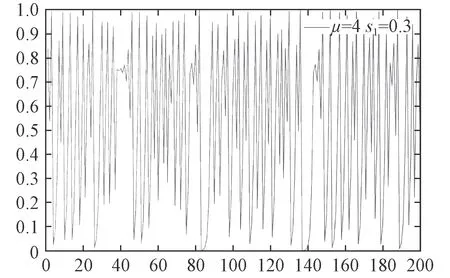
图 1 μ=4 τ=0.3Fig.1 μ=4 τ=0.3

图 2 μ=4 τ=0.6Fig.2 μ=4 τ=0.3

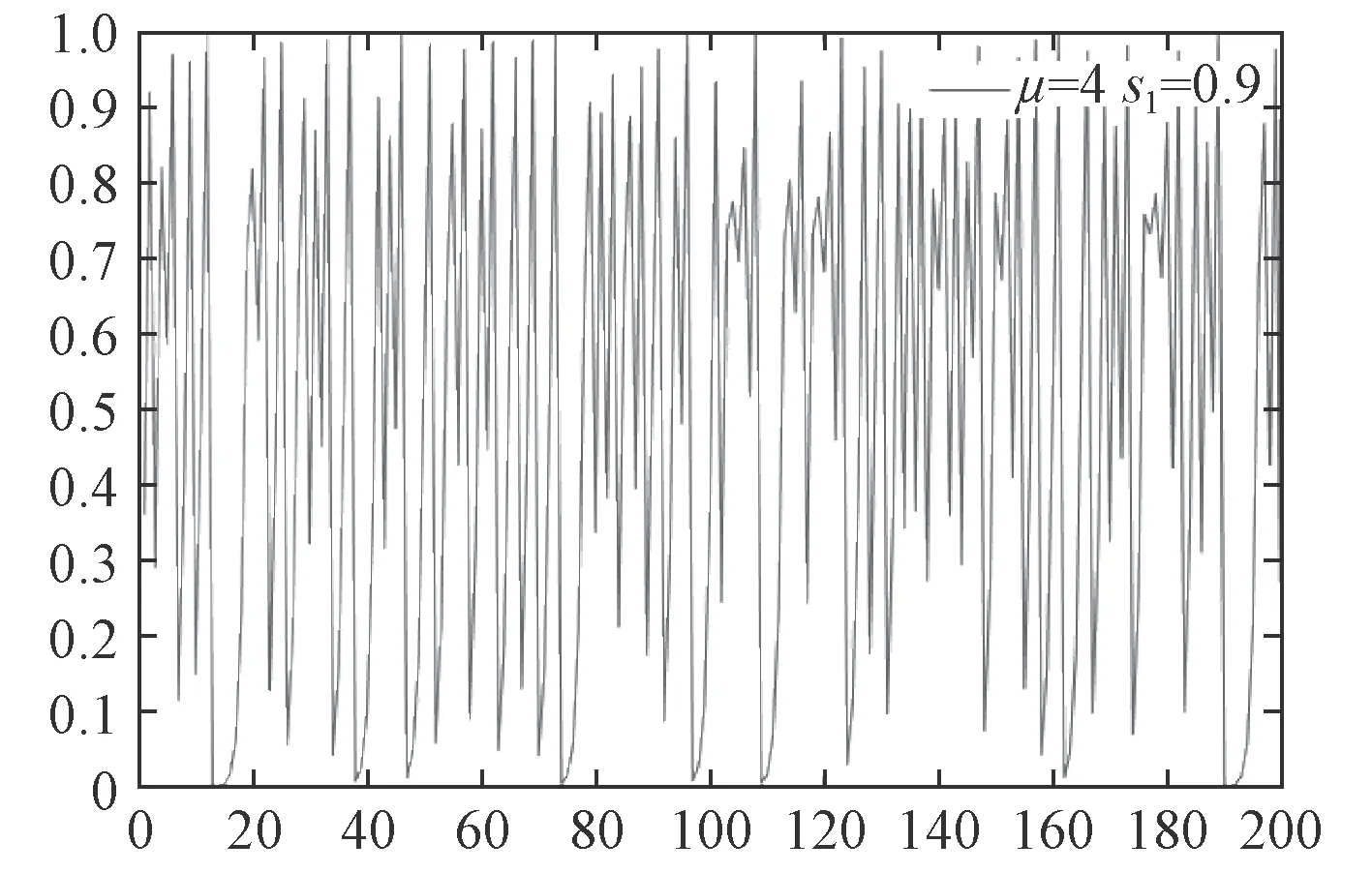
图 3 μ=4 τ=0.9Fig.3 μ=4 τ=0.9

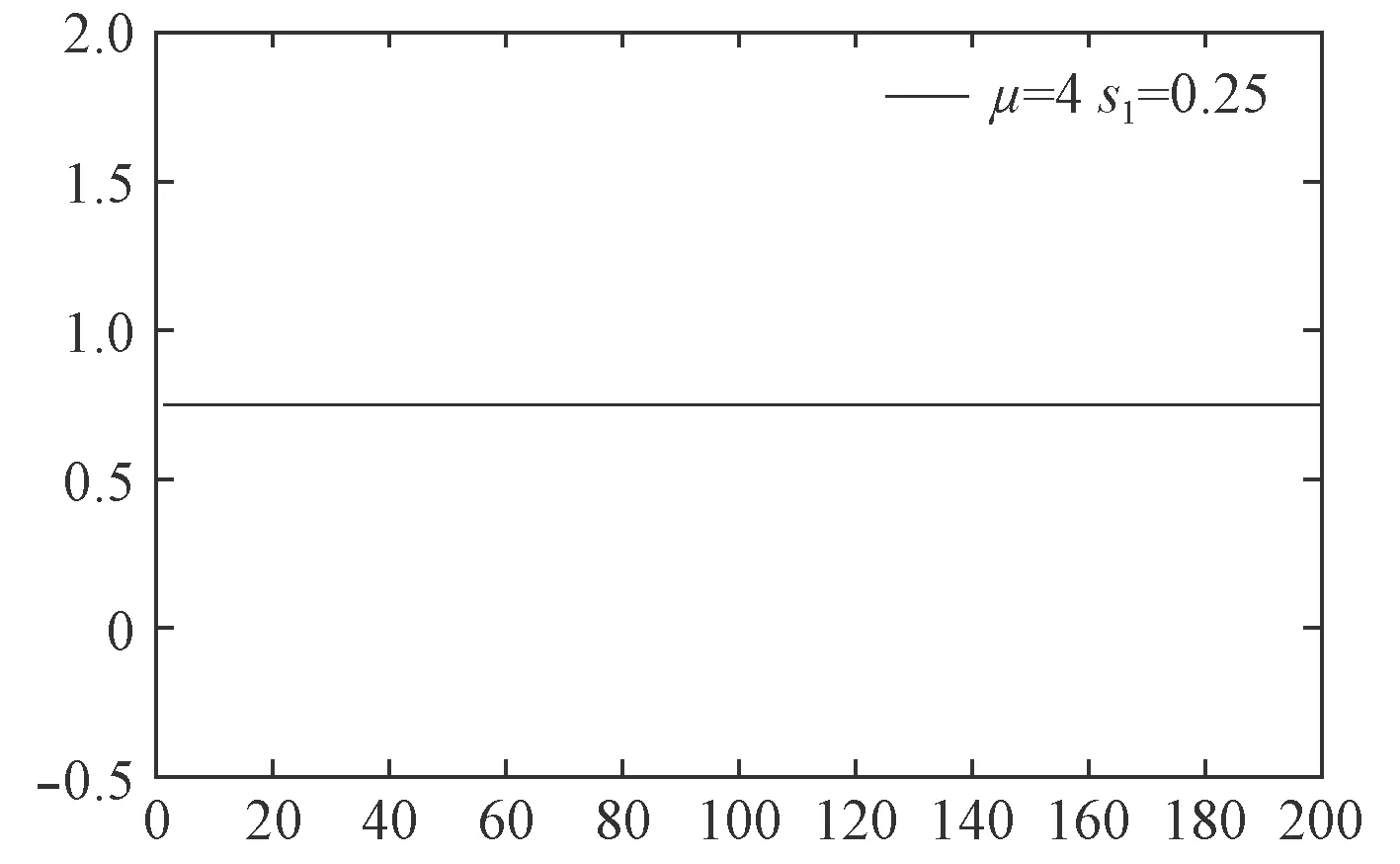
图 4 μ=4 τ=0.25Fig.4 μ=4 τ=0.25

当雇佣蜂转变为侦察蜂时，将产生一个D 维随机向 量 τ0=[τ01,τ02,···τ0D]， τ0∈[0,1]并 不 等 于 特 殊 值。τ0作为初始值，由Logistic 混沌映射式得到蜜源附近多个邻域解，从而得到经混沌操作后的新蜜源：

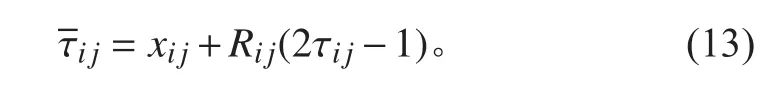
目的是 将 τij映射到 优化变量上，是在 雇佣蜂所在的蜜源为中心，以 Rij为半径的区域上。算法流程图如图5 所示。

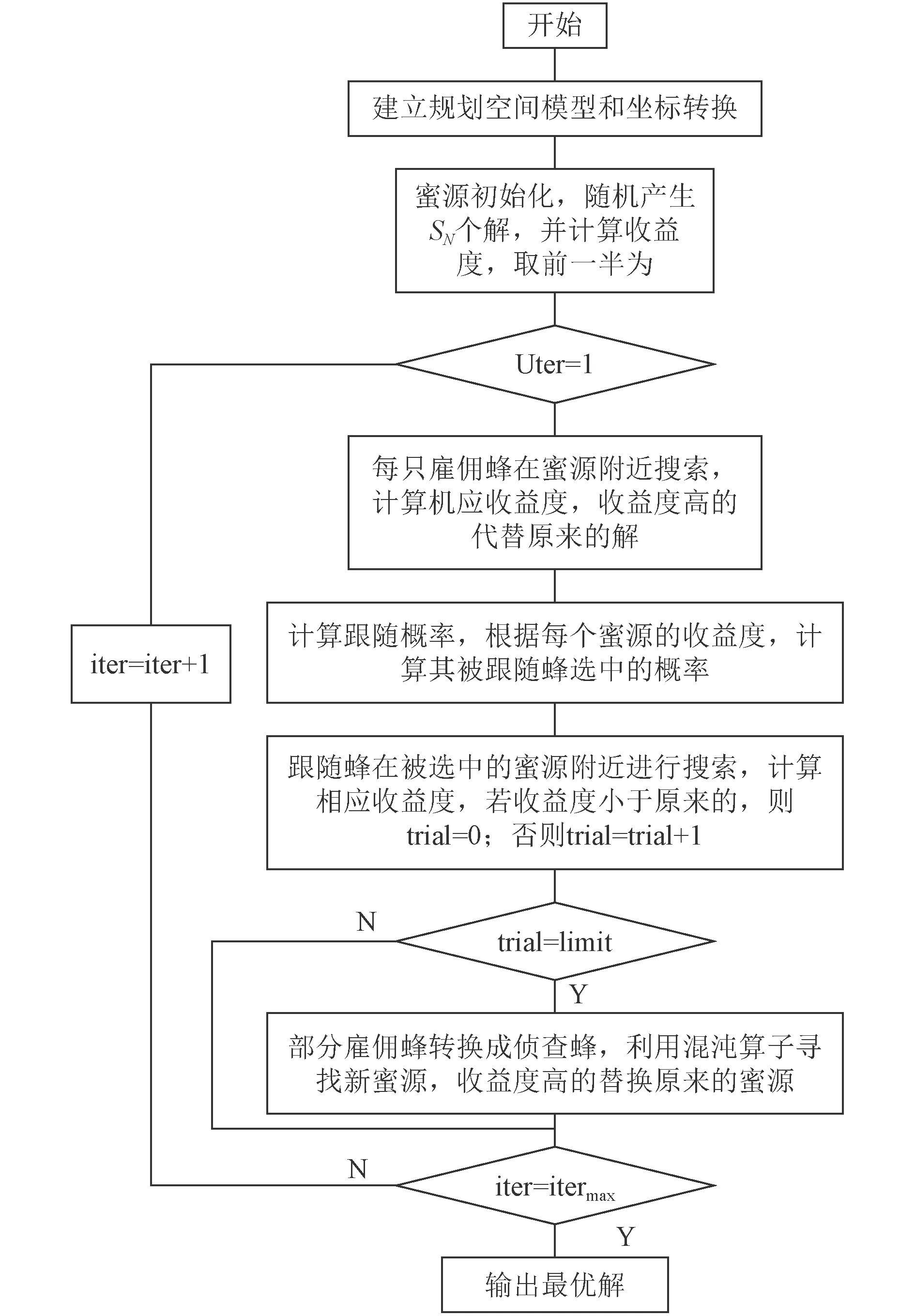
图 5 算法流程图Fig.5 Flow chart of algorithm

1）建立栅格化环境模型。

2）设置混合混沌ABC 算法的基本参数，包括种群大小，最大迭代次数itermax，当前迭代次数iter，蜜源数量。

3）雇佣蜂阶段，根据蜜源更新公式随机搜索附近新蜜源，贪心原则，选择更优的蜜源位置。

4）侦察蜂阶段，根据概率选择公式，对雇佣蜂所分享的蜜源信息进行选择。

5）侦察蜂阶段，重新根据蜜源更新公式在新被选中的蜜源附近进行搜索，计算收益度，收益度高的置为当前蜜源，否则不变。

6）迭代进行，当蜜源未更新次数达到limit 值，雇佣蜂转变为侦察蜂，利用混算搜索算子搜索新蜜源。

3 算法仿真

蜜源表示可能的最优解，即设置在Win10 环境下，基于Matlab2016b 安照表1 初始化数据进行仿真计算，结果如图6～图9 所示。

表 1 初始化数据Tab.1 Initialization data

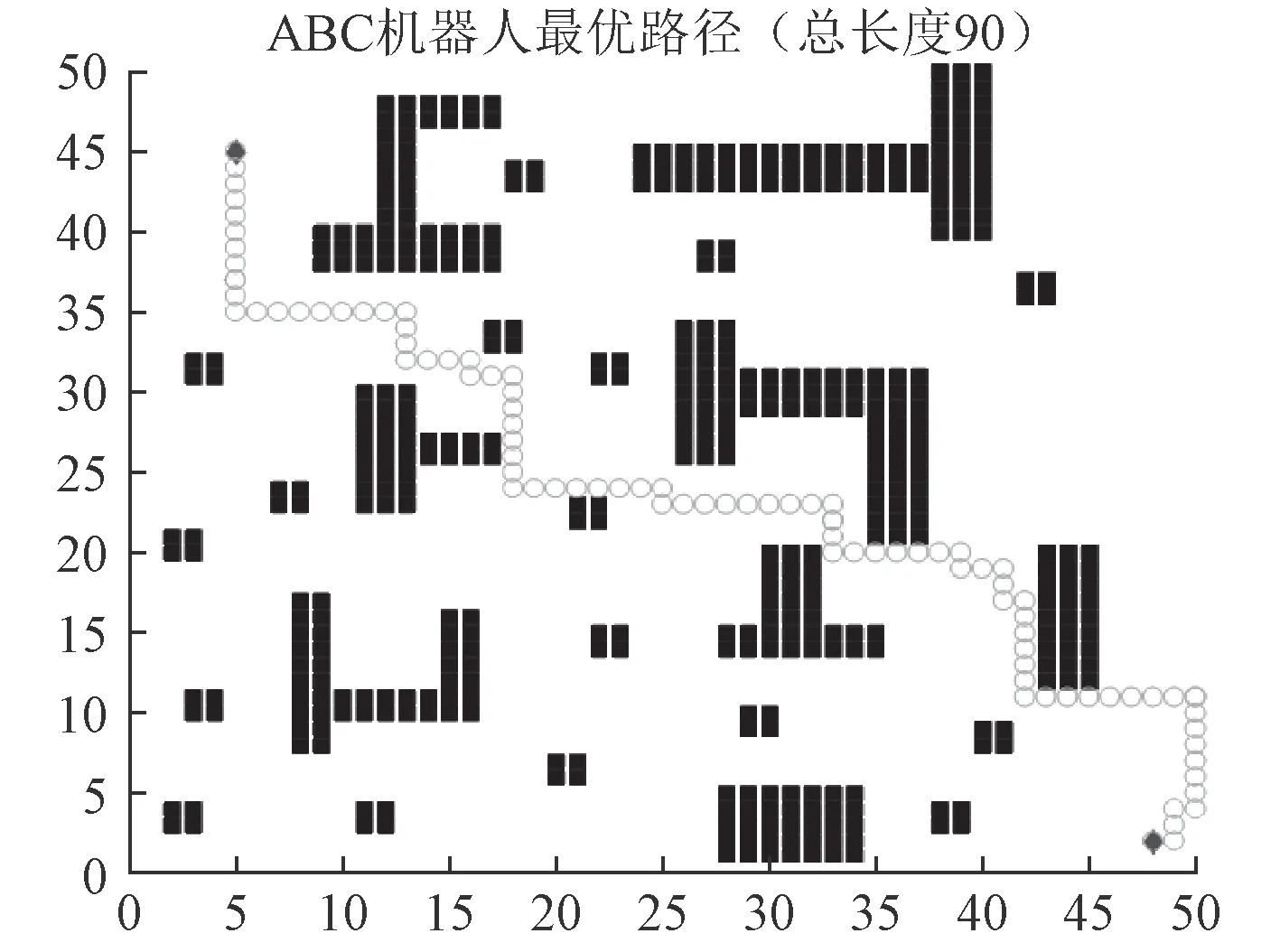
图 6 传统ABC 算法路径结果Fig.6 Path results of traditional ABC algorithm

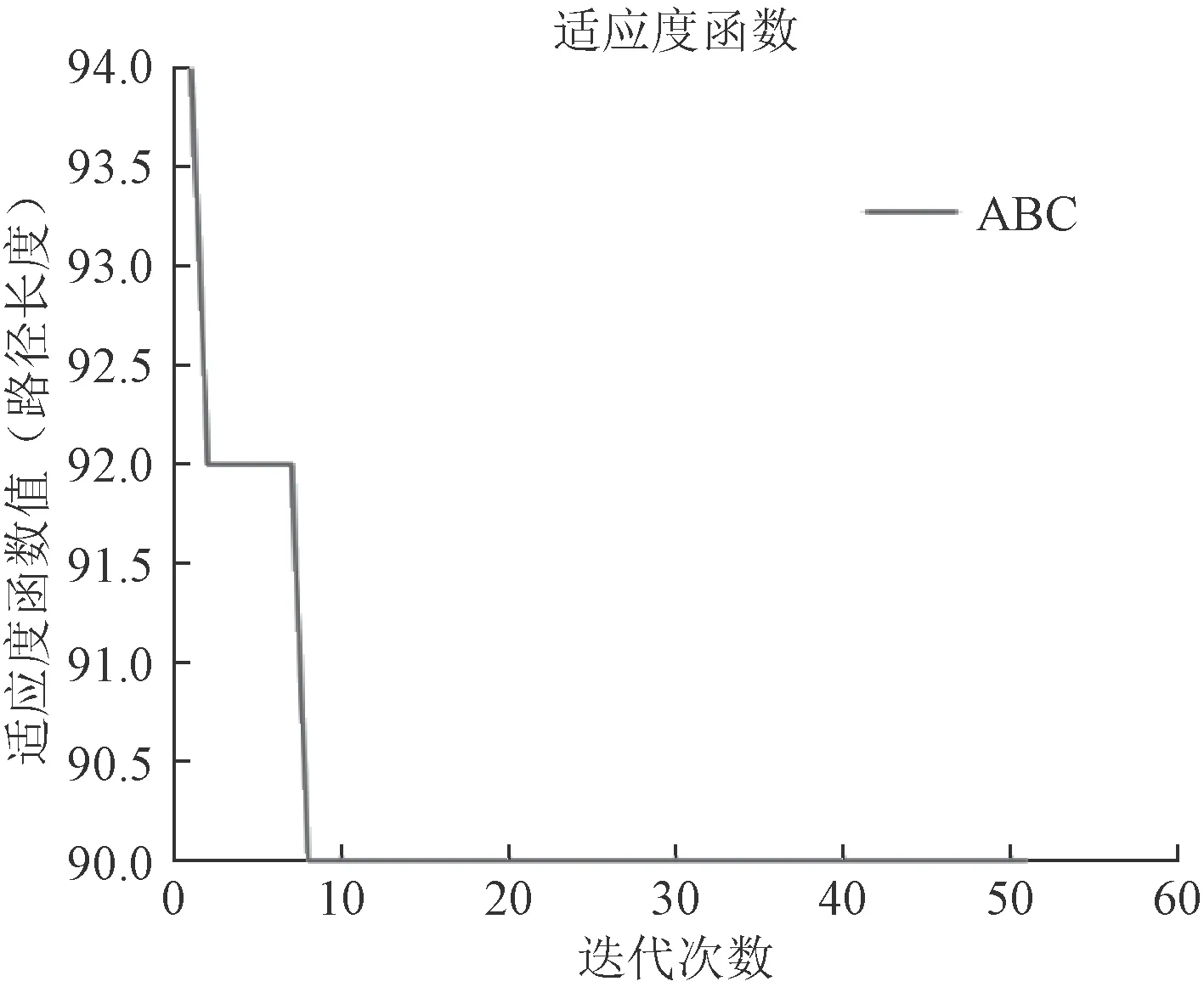
图 7 传统ABC 算法迭代图Fig.7 Iterative diagram of traditional ABC algorithm

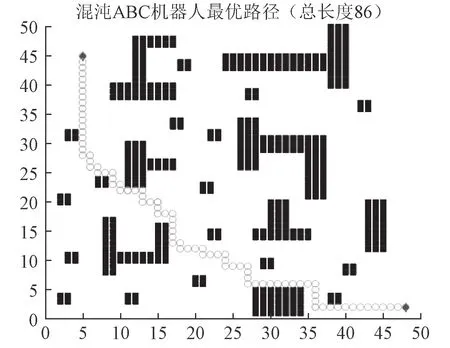
图 8 混沌ABC 算法路径结果Fig.8 Path result of chaotic ABC algorithm

由图6 和图7 可以看出，改进后的混沌ABC 算法比传统ABC 算法明显降低了路径长度。由图8 和图9可以看出，改进后的算法有效避免了ABC 算法的早熟收敛问题。

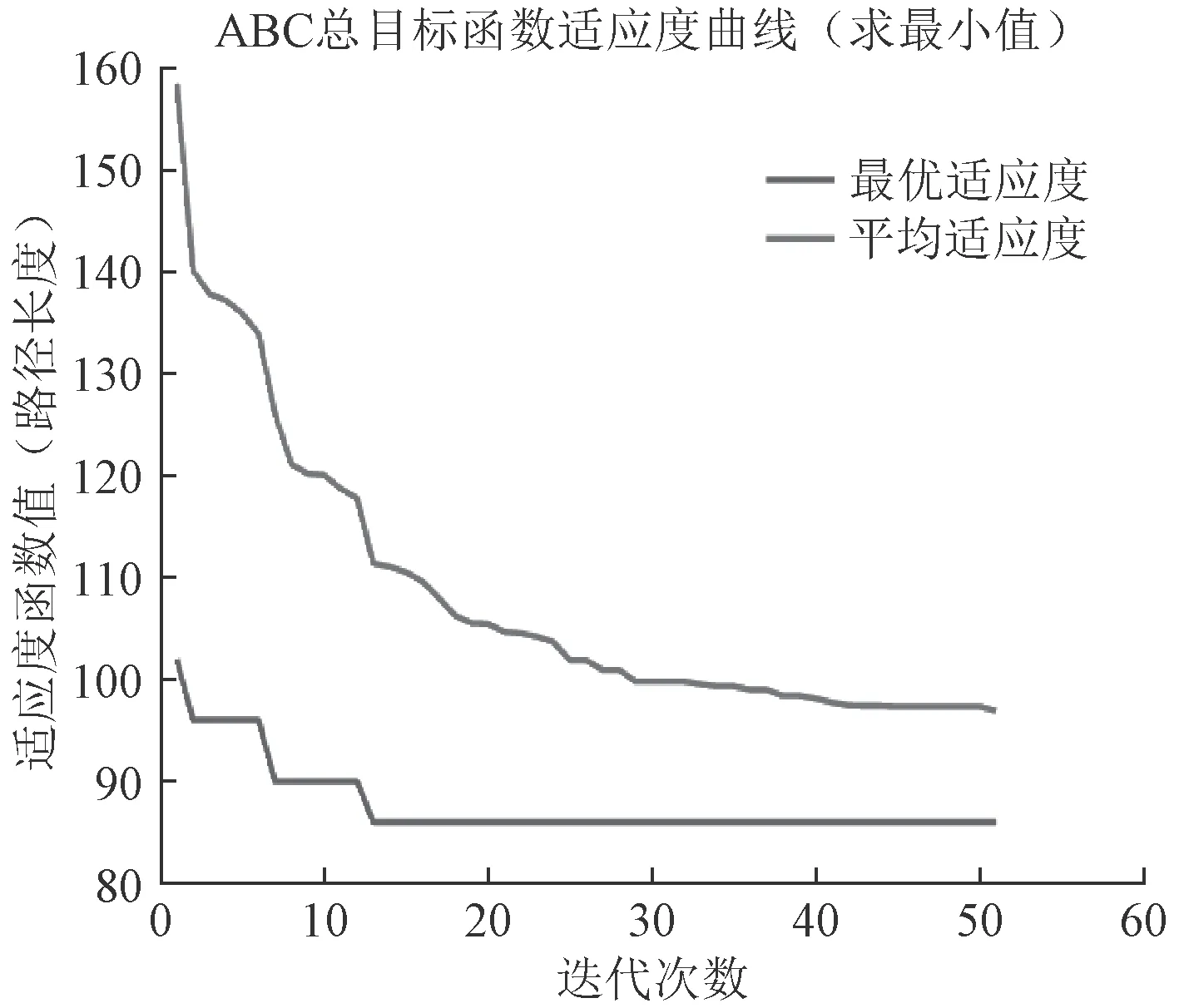
图 9 混沌ABC 算法迭代图Fig.9 Iterative diagram of chaotic ABC algorithm.

4 结 语

提出结合混沌局部搜索算法的改进人工蜂群算法，用以解决USV 的路径规划问题。该算法利用Logistcis 混沌序列的全空间遍历特性避免ABC 算法陷入局部最优，从而快速找到全局最优解。算例测试表明，与传统蜂群算法相比，改进后的算法在求解质量上有了提升，能够有效解决传统ABC 算法局部收敛的问题，避免早熟收敛，并能为无人艇规划出一条可通行且较优的路径。