基于动态贝叶斯网络的无人船推进系统PHM 技术

王天语，王鸿东，梁晓锋，易 宏

(1.上海交通大学 海洋工程国家重点实验室，上海 200240；2.上海交通大学海洋智能装备与系统教育部重点实验室，上海 200240)

0 引 言

得益于现代工业，尤其是自动驾驶技术的迅猛发展，以及世界性的对于海洋军事、商业问题兴趣的增加，无人船领域在近几年得到广泛关注。智能无人船可以代替传统船舶，在更加苛刻危险的环境条件下执行任务，或协助其进行大规模的商业贸易行动。与此同时，故障预测和健康管理（prognostic and health management，PHM）技术被用来进行对无人船系统和组件进行预期工作时间的分析，以提升无人船的工作效能。PHM 技术通过评估系统偏离正常运行条件的程度，预测组件的未来性能。通过监测磨损和老化的迹象，给出系统故障预警。将故障机制研究与生命周期管理进行关联，从而实现即时评估无人船健康状况，实现维修保障的智能辅助决策。

对于无人船而言，其PHM 技术需求与传统船舶有所区别。传统的船舶维修保障方式主要通过人工经验对故障进行分析，以实验的方法确定具体的故障内容，这种方式的准确性和时间效率已经难以满足当前的要求。传统的观念中对于维修保障重要性的认识不够、维修人员专业知识和技能储备不足，船舶的安全性受到一定影响。由于无人船本身没有随行人员进行监控和维修，采用事后维修的方法难以满足无人船的使用需求，这对无人船健康管理技术的实时性和自主性提出了要求。此外，相较于传统船舶而言，无人船的控制、通信系统复杂度更高，而且执行任务的环境可能更加恶劣。因此，需要研发相应的自主检测系统进行实时健康诊断，使无人船具备快速响应与处理复杂问题的能力。所研发的系统需要对无人船未来工况进行预测，并在故障发生前进行预警，达到预防性维修保障的目的。另一方面，近年来传感器获取实时状态数据能力的增强，数据处理技术的发展和数据分析能力的提高，为无人船开展实时监测，并进行维修保障智能决策提供了条件。

传统的PHM 方法主要包括基于物理模型、基于经验模型或基于数据驱动等[1]。基于物理模型的方法在一定的物理基础上建立模型，例如通过建立动力学模型计算载荷以估算剩余寿命等[2]；基于经验模型的方法则通过数学函数等形式，用无实际意义的参数描述模型，例如借助模糊逻辑的方法建立模型处理医疗诊断问题等[3]。基于数据驱动的方法则是利用已有的数据，进行建模分析，如在医学诊断中常采用神经网络[4]、支持向量机[5]等方式进行建模诊断分析。贝叶斯网络是一种基于数据驱动的模型，可以完全依赖已有的数据进行结构学习和参数学习。贝叶斯网络的方法已广泛应用于国内外工程PHM 相关技术中。实例如JT Zhang 等[6]使用贝叶斯网络量化海底系统的可靠性；Pui 等[7]利用贝叶斯网络对海上钻井作业进行了动态风险维护等，均是贝叶斯网络模型在故障诊断与健康管理方面的成功应用。

PHM 技术在船舶系统的故障诊断与健康管理当中已经有了一些应用。美国麻省理工学院通过振动信号的采集和特征提取，研究了柴油机振动和主机压力的关系，实现了对船舶主机的故障诊断[8]。刘晶等[9]利用网络进行数据传输，针对船舶的机电控制设备故障诊断问题做出了研究，但该方法在实时性上有所欠缺。

本文针对无人船的PHM 问题，采用视情维修的策略，通过对无人船设备状态进行实时监测，达到对设备未来状态进行可靠预测的目的。通过动态贝叶斯网络模型，建立无人船当前工作状态与下一时刻健康状态的关系，对船舶未来健康状态进行实时评估，以满足预防性维修保障的要求。通过全面的安全监控、异常预警、综合诊断、故障预测与健康评估，可以充分评估船体在不同状态下的实际工作能力，辅助岸上人员安排调整无人船的工作目标，较大提升无人船的任务实现能力。

1 理论基础

1.1 贝叶斯网络

贝叶斯网络是一个概率图模型，通过有向无环图（directed acyclic graph, DAG）来表示一组随机变量以及其中的依赖关系。这一概念最早由J.Pearl 在1982 年提出[10]，用概率表定量表达每个节点和父子节点之间的条件概率[11]。网络用节点表示论域中的随机变量，其边与一个节点对另外一个节点的直接影响相对应。由此带来的组成成分是一系列的局部概率模型，用于表示每个变量对于其父节点依赖的本质[12]。

假设有全集U 包含n 个随机变量X1, X2, ···, Xn,U={X1, X2, ···, Xn}，那么其联合概率可以表示为：

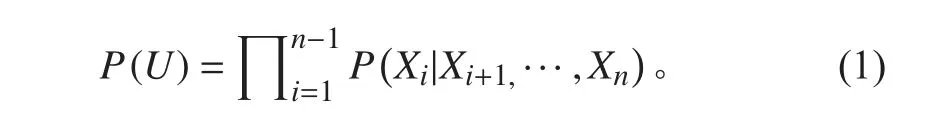
通过联合概率的分布P(U)，可以计算出各个边际概率和条件概率。对于一组离散变量Xi，其统计证据以似然分布的形式出现，再通过网络变量的观察值在给定条件E 之下的条件概率：

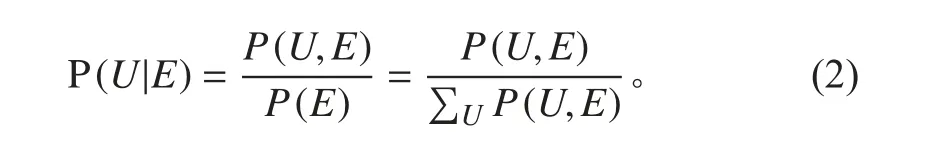
在建立和使用贝叶斯网络模型时，首先需要通过因果逻辑或其他结构学习进行贝叶斯网络的结构学习，随后根据已产生的数据集对网络进行训练，即进行参数学习。对于已建立起的贝叶斯网络，通过对节点状态观测来判断和预测系统故障。

1.2 动态贝叶斯网络

为了研究现有模型当中的时序信息，使用动态贝叶斯网络来学习和处理动态的系统模型[14]。动态贝叶斯网络用来表达一个跟随时间而不断变化的模型，是一个跟随毗邻时间步骤把不同变量联系起来的贝叶斯网络，并且通过上一个时间点的模型推算当前时间点的模型取值。

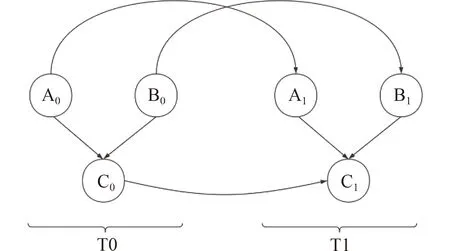
图 1 动态贝叶斯网络图Fig.1 Dynamic Bayesian network graph

如图2 所示，假设故障原因A 和故障原因B 都会导致故障C，其在时间T0时刻的模型节点用A0, B0, C0表示，在其后毗邻的时间点T1时刻的模型节点用A1,B1, C1表示，则在T1时刻内各个节点的父节点不再仅仅是原本的网络结构中的父节点，同时增加了上一时刻的个节点的状态。

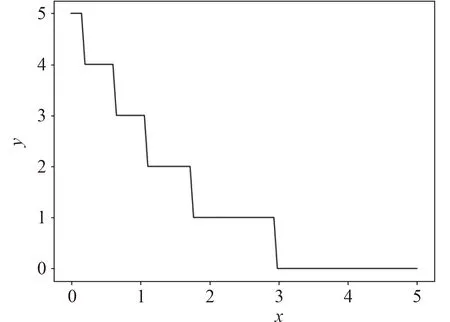
图 2 数据离散化示例Fig.2 Data discretization processing example

2 基于动态贝叶斯网络的无人船PHM 模型

2.1 无人船监测数据处理方法

在对无人船开展PHM 工作时，首先要通过传感器实时获得船体的动态监测数据，通过数据处理才能进行后续的分析诊断。无人船的监测数据时序上是连续的，将其应用于贝叶斯网络进行处理的前提是将连续数值离散化处理。在应用贝叶斯网络等具有节点的智能决策模型时，离散的节点取值更便于快速运算与响应，因而信号数据最终的离散化处理能大大提升整体运算的性能。

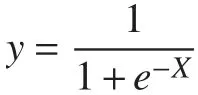
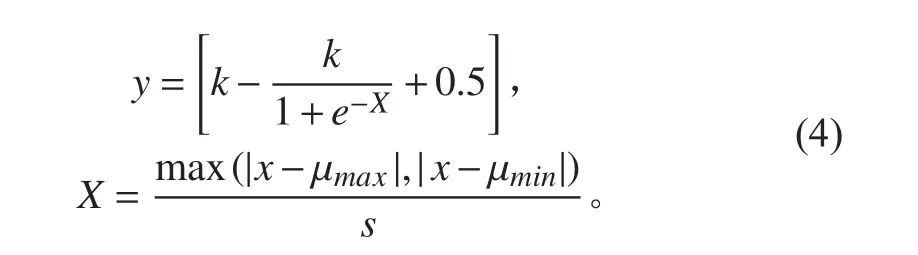
式中：y 为节点的实时评分；k 为节点评分数目参数；e 为监测点期望值；x 为监测点观察值；μmax为监测数值范围最大值；μmin为监测数值范围最小值；s 为监测节点敏感程度。

举例说明其进行评分的方法。在给定的k 为10 情况下，评分可以划为0～5 的6个离散取值，其对应的归一化的偏离值X 与节点评分y 的关系如图3 所示。

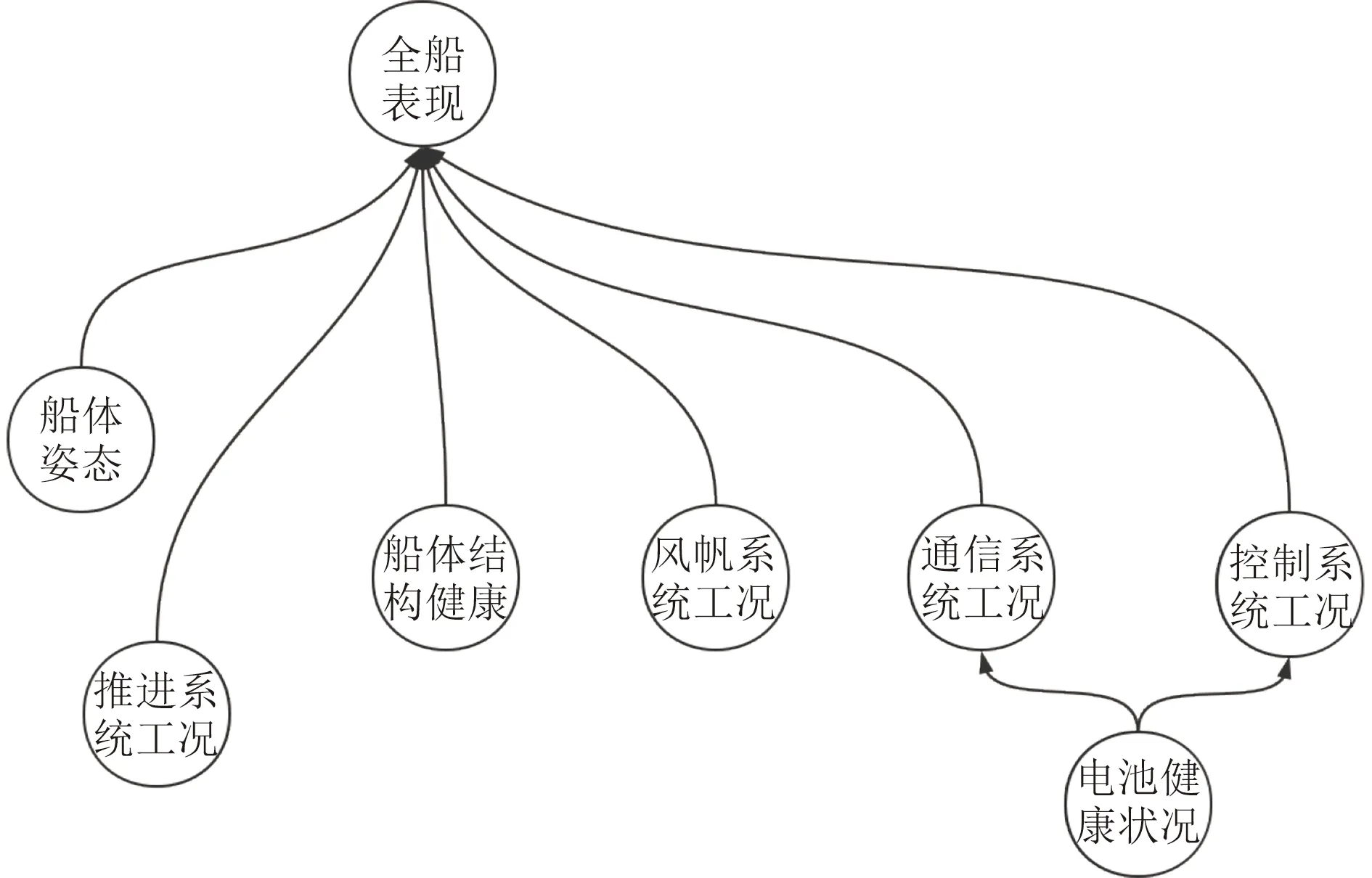
图 3 全船PHM 模型Fig.3 Ship's PHM model

对于贝叶斯网络模型，通过将各个节点的监测数值归一化为简单的评分机制，模型的运算量和复杂度将被大大降低，同时可以进行直观在线显示各个节点的工况，便于后续模型的构建和健康监测的设计处理。

2.2 无人船PHM 模型总体设计方案

本文选取上海交通大学海洋智能装备与系统教育部重点实验室设计、制造的风帆无人船[13]为例，进行PHM 的模型设计。选取的监测点包括全船表现、船体姿态、推进系统工况、船体结构健康、风帆系统工况、通信系统工况、控制系统工况8 个总体节点，以及每个节点对应子系统的节点构成贝叶斯网络的变量。其底层节点由船体动态监测中的振动监测、电源电压监测、陀螺仪和结构应力监测等完成。为了具体表现PHM 模型的应用场景，选取推进系统进行详细的模型构建与检测方案设计，并对模型性能进行测试评估。

2.3 推进系统监测方案与模型

振动分析是用于旋转机械状态监测的最成功的技术之一，是诊断电机等元件机械问题的一种非常高效和便捷的工具[16]。当机械结构发生异常时，振动的频率和幅值会相应的发生变化。通过传感器采集信号，将采集信号通过短时傅里叶变换进行提取，并与已知的故障模式进行比较，即可判断出其工况以及潜在的故障可能[17]。

在该船的推进系统中主要选取主机、螺旋桨、轴系三部分作为贝叶斯网络中的节点。根据振动类型的不同，推进系统中的振动可以分为扭转振动、轴向振动、垂直轴系振动三类。

在船舶正常推进时，主机通过轴系连接螺旋桨，通过带动轴系旋转引发螺旋桨的旋转，故该部分的旋转振动由主机提供激励，而扭转振动的系统结构可以简化为主机到轴系到螺旋桨的顺序，其振动频率应当与主机正常工作时设计的频率相当。

图 4 推进系统扭转振动示意Fig.4 Thrust system torsional vibration

推进系统的轴向振动则是由螺旋桨传递到轴系再传递到主机。由于螺旋桨在转动时单个桨叶在转动起始点和终点处收到的水流作用不同，其轴向收到的推力也随之发生变化。当螺旋桨连续旋转时，在沿轴线方向会产生周期性的交替推里，即螺旋桨的轴向激励，其频率为螺旋桨每分钟转速乘以其桨叶数量。

图 5 推进系统轴向振动示意Fig.5 Thrust system axial vibration

除此之外，推进系统工作时还会产生垂直于轴系的振动。由于轴的弯曲，轴的重心与轴的理想中心线不重合，因此当轴旋转时，重心上的离心力将使其进一步远离理想的中心线，从而导致其在垂直于轴系的方向发生振动。该振动的频率应与其旋转速度保持适应。

根据上述3 种振动监测方案设计，加之对于主机温度的实时监控，可以构成推进系统的整体贝叶斯网络，其结构如图7 所示。

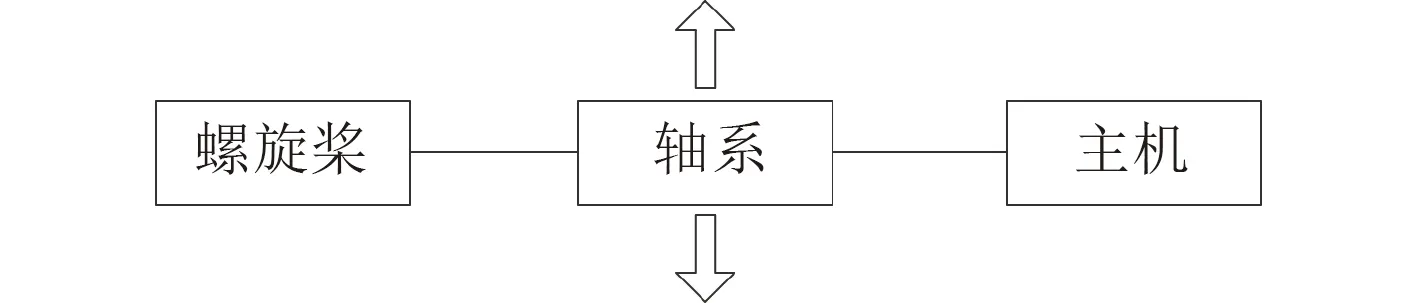
图 6 推进系统垂直轴向振动示意Fig.6 Thrust system vertical axial vibration

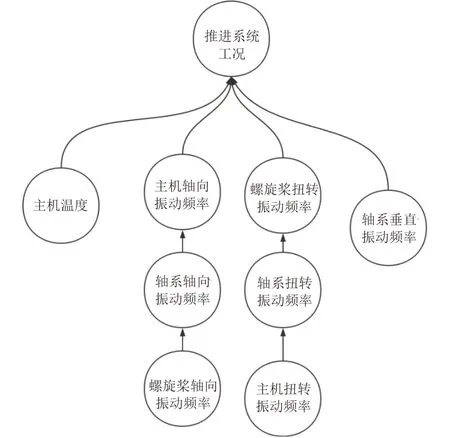
图 7 推进系统贝叶斯网络模型Fig.7 Thrust system Bayesian network model

2.4 推进系统动态贝叶斯网络模型算例

在动态贝叶斯模型中，相邻2 个时间片中的贝叶斯网络的底层节点被连接起来。在诊断过程中，故障信号往往不会随时间而直接消失，即上一个时间片的故障特征很大程度上会保留至紧邻的一个时间片中，其动态贝叶斯网络模型如图8 所示。随后进行动态贝叶斯网络模型进行简化，相当于为底层节点依次增加1 个子节点，为对应的上个时间片的状态。贝叶斯网络可转化为如图9 所示模型进行表示，其中虚线连接部分节点表示上一个时间片中的节点数值。

通过无人船监测数据进行对样本的参数学习，即可得到推进系统工况关于各个子节点取值的概率分布情况。根据式(2)，令其中U 为节点推进系统工况的具体取值，E 为已有的观测数值，即可得到在当前状态下船舶推进系统健康状态的预测分布，此即系统中进行的推理过程。对于动态贝叶斯网络在健康管理系统中的运用的具体效果，给出算例加以演示。

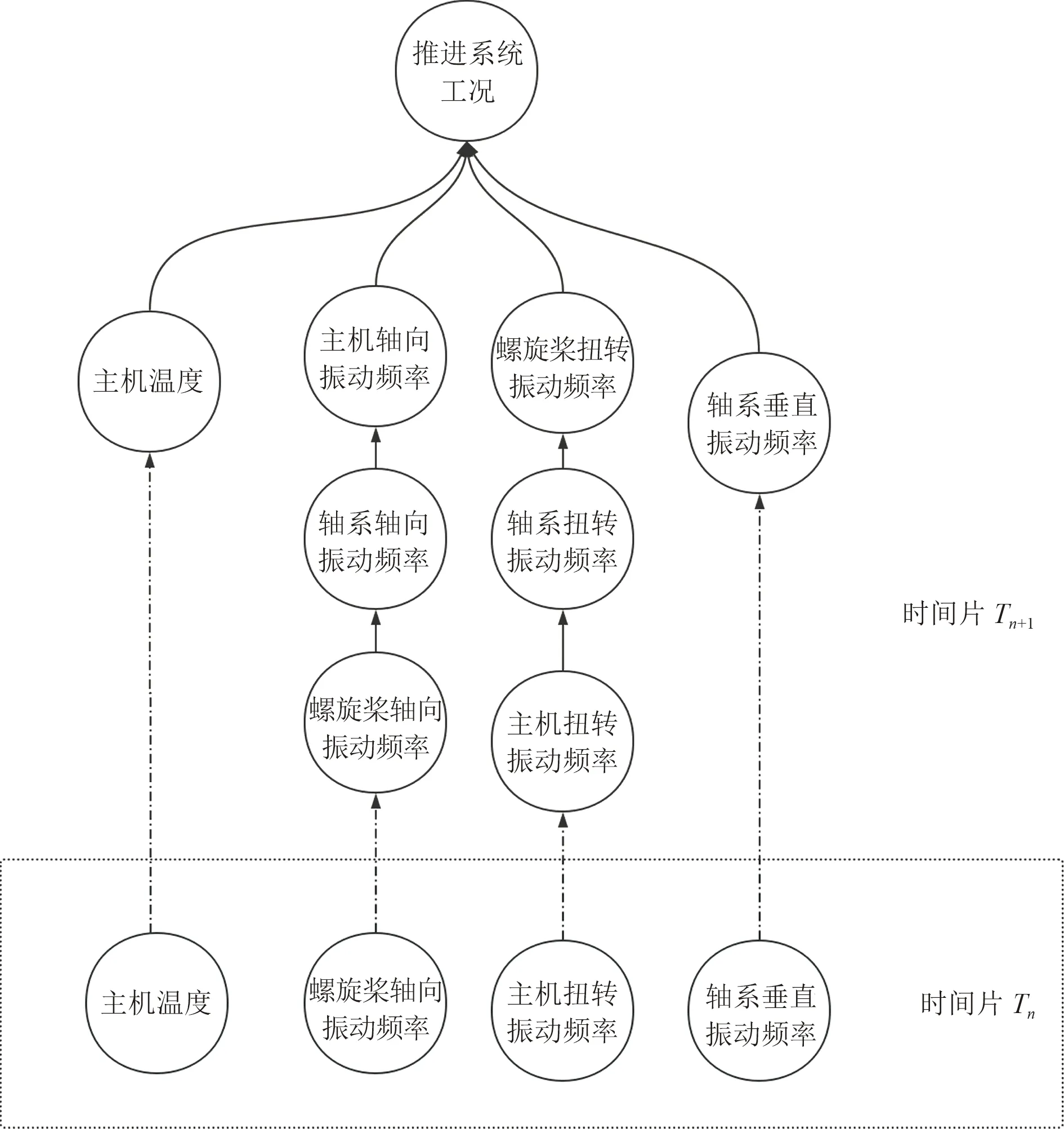
图 9 简化动态贝叶斯网络模型Fig.9 Simplified dynamic Bayesian network model

现将各个节点所对应观测点健康状况划分为1～3 评分，分别代表危险、有风险和运行良好。在本系统中每次监测数据的输入间隔为1 min，即2 个时间片之间的间隔为1 min。在此例中根据元件故障率及分布概率等条件模拟生成20 000 个样本数据集，数据包括某一时间所有节点的取值情况，用以测试模型是否能准确反映故障分布的概率关系以及响应速度。模型通过MLE 参数学习的方式得到动态贝叶斯网络的条件概率分布。取时间片T0样本数据，并记其后3 个时间片分别为T1，T2，T3。T0时通过监测数据知所有节点数值均为3，即运行状况良好。用TTi，FPTi，FETi，FSTi分别代表在Ti时刻的主机温度、螺旋桨轴向振动频率、主机扭转振动频率、轴系垂向振动频率4 个节点的取值，用Th 代表推进系统工况节点的数值，则有TT0=FPT0=FET0=FST0=3，将其作为观测值代入T1时刻的动态贝叶斯网络，可根据式(2)分别得到P(Th=1|E),P(Th=2|E),P(Th=3|E)的取值概率分布如表1所示。

表 1 T1 时刻Th 节点状态概率分布Tab.1 Th node state probability distribution at time T1

在T1前所有节点工作正常，而在T1时刻由于轴系偏心加大等原因，轴系垂向振动频率明显偏离正常取值，即FST1节点数值降至2，其他节点数值保持不变。将TT1=FPT1=FET1=3，FST0=2 作为观测值代入T2时刻的动态贝叶斯网络，对此时的贝叶斯网络做条件概率分布因式分解得到当前网络的Th 节点取值概率分布，可以得到其概率分布如表2 所示。

表 2 T2 时刻Th 节点状态概率分布Tab.2 Th node state probability distribution at time T2

动态贝叶斯网络，对由于T1时刻轴系振动发生的变化，系统将认为在T2时刻系统有风险的概率大大增加。如果在T2时刻轴系垂向振动的偏离程度进一步加剧，即FST2节点数值降至1，其他节点数值保持不变，对应预测T3时刻的推进系统工况概率分布将如表3所示。

此时由于轴系振动已经达到了危险程度，系统预测在下一时刻推进系统整体评价为危险的概率大大上升。上述3 种情况指明了系统对于每个子节点变化进行风险评估的能力，通过将更复杂的、更多节点综合成全船的动态贝叶斯网络模型，可以对全船工作状况进行实时监控与风险预测，达到健康管理的目的。

表 3 T3 时刻Th 节点状态概率分布Tab.3 Th node state probability distribution at time T3

在上述算例中，船舶在T 2 时刻的有风险概率＞0.5，而危险概率＞0.3，即轴系振动带来的潜在风险大于系统设定的阈值时，系统将选择停止任务而进行靠港维修。同时对于在岸人员，系统可以根据轴系振动故障的可能原因和历史故障案例，提供相应的排查建议和维修策略。采用动态贝叶斯网络的方式避免了无人设备在发生故障时既无法完成既定任务，也无法维修的场景出现。动态贝叶斯网络模型反映的是当前工况对下一时刻故障概率的影响，对于工作风险较大的无人船选择停止任务寻求检修，从而达到预先维修保养的目的。

3 系统评价

3.1 排序概率评分评价

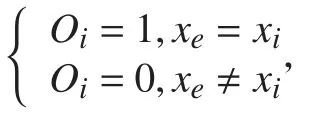
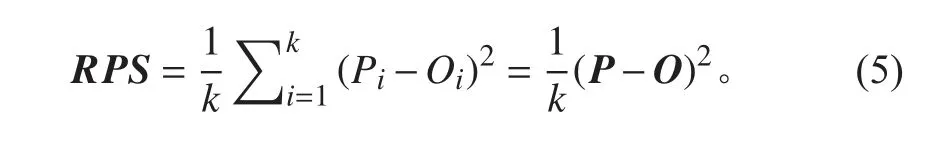
根据上式，RPS 是一个处在0～1 之间的具体评分数值。显而易见的是，预测概率越准确的模型，其RPS 数值就会越小。针对不同样本学习情况的模型准确性，计算不同样本数据大小的PRS 计算，其结果如图10 所示。

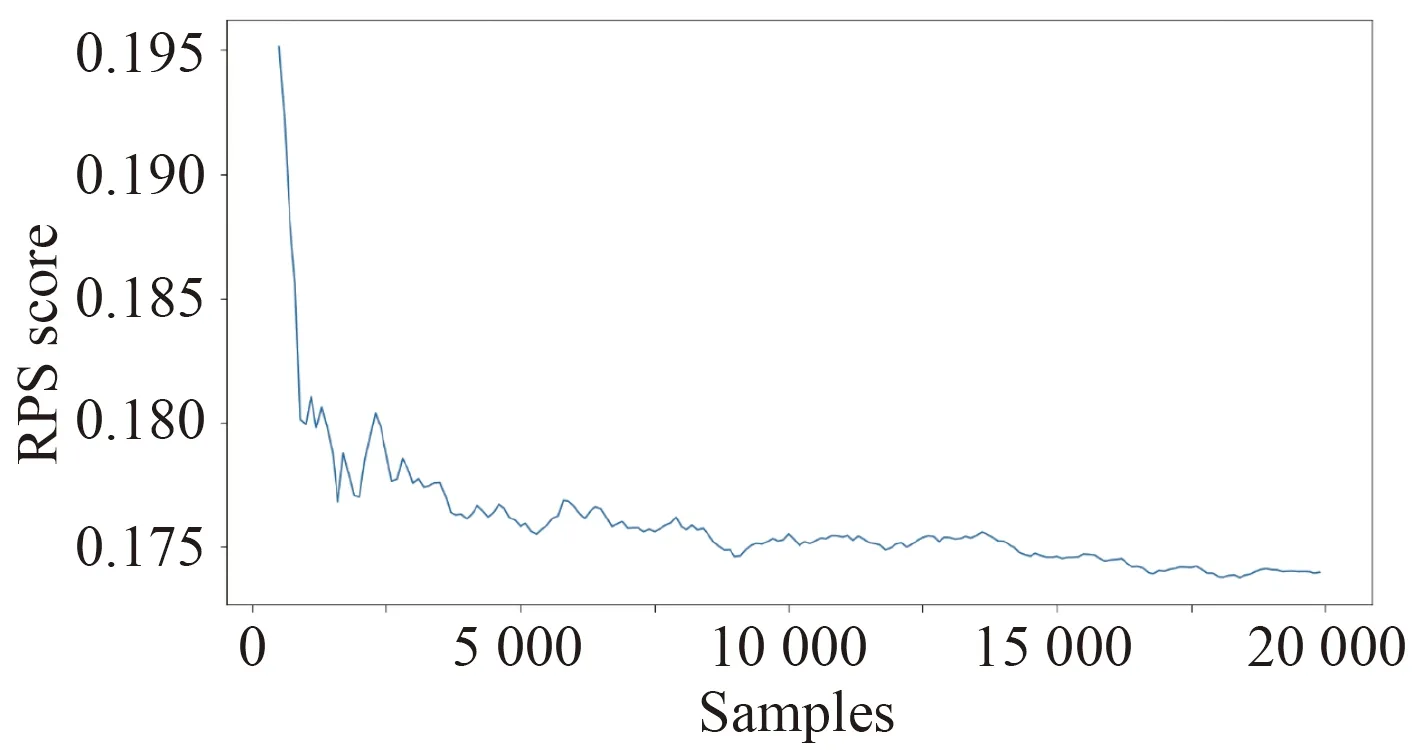
图 10 RPS 随样本数的变化Fig.10 RPS changes with the number of samples

当样本数据过小时，故障信息并不完全，贝叶斯网络中的部分概率分布会缺失，RPS 检验的评分较高。当进行参数学习所用的样本数据集逐渐增加时，模型的RPS 评分迅速减小。当样本数量达到15 000 个时，RPS 评分小于0.175，体现了模型对于当前故障信息的准确还原能力。在实际使用中，伴随着获得的故障信息逐步完善，模型准确预测故障避免风险的能力也会随之提高。

3.2 系统实时性评价

对于实时监测的PHM 模型而言，除了需要能够做出准确的判断，还需要PHM 模型能在足够短的时间内做出判断，即拥有足够的实时性。为了评价PHM 模型是否能够快速响应，评价模型两方面运算的速度，共分3个实验组别进行5次实验计算其平均耗时：1)模型对20 000 个样本进行参数学习，更新概率分布所需的时间；2)系统根据当前所的观测值进行推理计算，预测下一时间片健康程度的时间；3) 利用for 循环计算1～106的整数求和的时间。其中第3 组作为对照试验组，以供不同系统工作平台等进行参考，避免由于平台算力差异带来的问题。测试结果如表4 所示。

表 4 系统实时性测试结果Tab.4 System real-time test results

观察测试结果可知，对于能够胜任一般循环加法的计算平台，模型的参数学习、推理计算等都有极快的运算速度。由于贝叶斯网络方法本身系统复杂度小而系统编写并未额外增加复杂度，本系统可以胜任实时监测推理计算的任务，显示出较好的实时性，适合在无人船上进行实时监测的PHM 使用。

4 结 语

近年来，随着无人船领域的发展，PHM 技术被用来进行对于其系统和组件进行预期工作时间的分析，以追求准确、即时的故障预测与风险评估。本文选取实验室设计的无人船为具体研究对象，设计了基于动态贝叶斯网络的无人船PHM 模型。基于动态贝叶斯网络，对给出的算例进行时序分析，证明通过动态贝叶斯网络进行船舶故障预警的可行性，完善了系统对于船舶健康管理方案的指导功能。基于动态贝叶斯网络的无人船PHM 技术可以在故障发生前进行预警，从而调整无人船工作目的及时检修，进行预防性维修保障工作。此外还对开发设计的PHM 模型进行准确性和实时性双方面评价，根据排序概率评分评估方案的准确性，可知所研发的系统通过对于故障案例的学习，可以准确地还原船舶的故障分布情况。通过实时性评估可知系统可以快速响应做出故障预测，充分体现船体在不同状态下的实际工作能力，辅助岸上人员安排调整无人船的工作目标，较大提升无人船的任务实现能力。在未来，无人船的PHM 技术可以涉及更多的船体系统并优化监测和评价方法，以求获得更为准确、即时的船体健康状态，充分评估船体在不同状态下的实际工作能力。