小水线面复合单体无人艇纵摇运动模式研究

余永强，杨松林，程占元

(江苏科技大学 船舶与海洋工程学院，江苏 镇江 212003)

0 引 言

小水线面复合单体船是由远离水线面的主潜体、支柱及在支柱上的“V”型水翼和上部结构构成。在航行时，易产生摇荡运动。其中纵摇是小水线面船舶在波浪中最容易发生的运动形式之一，且对航行时螺旋桨的推力产生较大的影响。因此，研究小水线面单体船的纵摇运动以及对其纵摇运动进行预报十分重要。通过大量实验发现，基于自航模试验或实船试验的系统辨识方法确定水动力导数，相较于其他方法简单、有效。在辨识技术和试验测量手段不断发展的今天，该方法具有广阔的应用前景。

本文建立基于遗传算法的系统辨识数学模型及方法，改编辨识软件，进行纵摇衰减运动模式的辨识分析，验证了系统辨识的可靠性，获得了该小水线面复合单体无人艇在静水状态下，纵摇运动衰减模式辨识方程及其水动力矩随时间的变化规律，完成了该无人艇纵摇衰减运动模式及其水动力矩变化的对比分析。证实试验值和预报值之间相对误差较小，拟合程度较好，证明该套系统辨识方法的可靠性。

1 静水纵摇衰减试验

1.1 试验模型

选用1 艘小水线面复合单体无人艇模型，其主尺度如表1 所示。

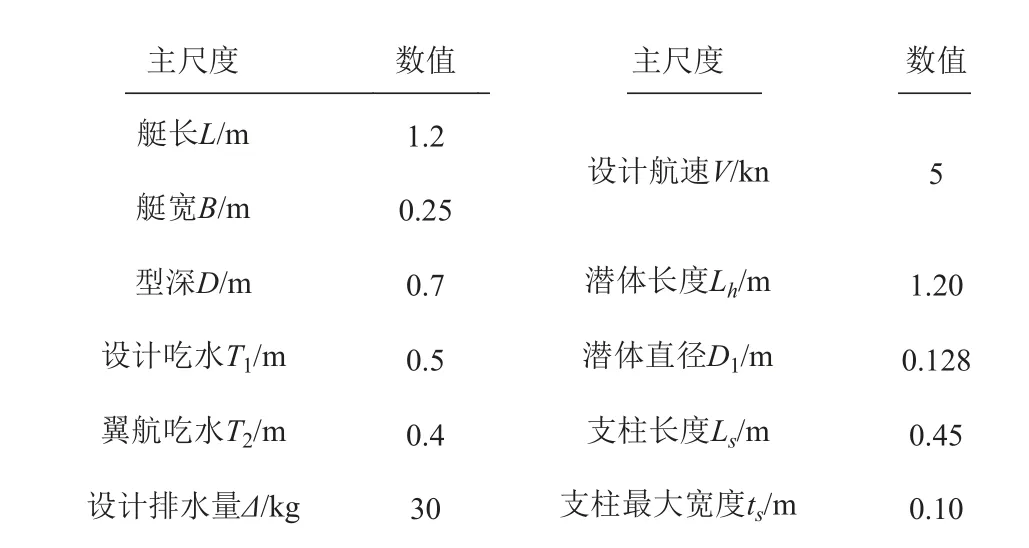
表 1 小水线面单体无人艇模的主要参数Tab.1 Main parameters of composite SWASH-USV model

三视图如图1 所示。

图 1 小水线面复合单体无人艇模型图Fig.1 Model of composite SWASH-USV

1.2 纵摇试验方案

本次试验在江苏科技大学的造波水池进行。为减小池壁效应，使艇模中横剖面垂直于池壁，并距离池壁较近一端保持不小于2 倍艇长的距离。本文主要通过测量艇模在静水中设计吃水自由衰减过程的纵摇角度变化，确定艇模的衰减规律。进行2 种吃水下，初始纵摇角度为2°，4°，6°，8°的纵摇试验。具体试验过程如下：

1）准备试验船模、MTi-G 惯性测量仪（可测船舶6 个自由度运动）、数据传输线、计算机。

2）将MTi-G 惯性测量仪水平放置在艇模重心位置处，通过数据线连接至计算机。

3）将艇模放置在水池中央，通过调节艇模配重使其处于正浮状态。

4）艇模达到正浮，通过MTi-G 软件读取艇模纵摇角，调整MTi-G 使其处于水平位置，使软件上显示的初始纵摇角在±0.2°之间。

5）待水面平静艇模稳定后，根据角度标记符号施加外力，以使艇模向艇首一侧倾斜。在释放外力的同时，利用MTi-G 测量仪开始采集数据，任艇模自由纵摇，待艇模重新稳定时，停止数据采集，读取MTi-G 软件显示的六自由度数据，保存试验数据。

6）重复步骤4 和步骤5 过程，改变所需初始纵摇角，设计吃水处的初始纵摇角共4 组，包括2°，4°，6°，8°。单次试验结束后，下次试验要等波浪消散水面平静后再进行。

试验过程如图2 所示。

图 2 小水线面复合单体无人艇静水纵摇衰减试验Fig.2 Pitch attenuation test of composite SWASH-USV in still water

2 基于遗传算法的系统辨识

2.1 系统辨识

辨识就是在测取研究对象给定的输入输出数据中，进行必要的数据处理和数学计算，确定一个与系统特性“等价”的模型。利用遗传算法为核心，C#语言自编系统辨识程序。

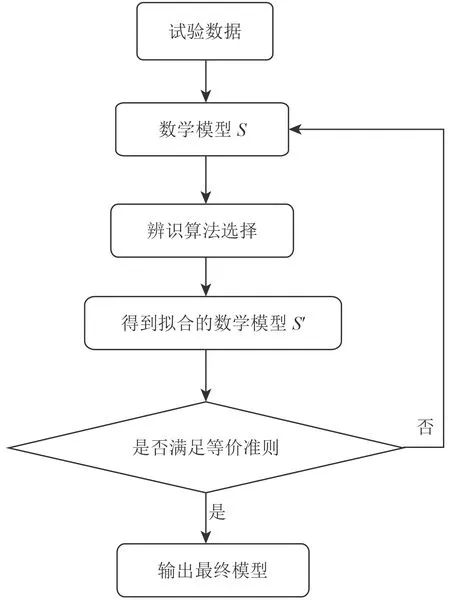
图 3 系统辨识流程图Fig.3 Flow chart of system identification

2.2 数学模型

考虑到本文的无人艇艇型特点，由于其沿首尾型体积变化较大，且尾部加装的舵和螺旋桨会增加旋涡阻尼等非线性阻尼力矩，但对于艇首尾型线缓慢过渡，且纵向曲率变化比较平缓，复原力矩满足初稳性公式。因此，为寻找适应本文艇模的纵摇方程，建立4 个辨识方程作为纵摇辨识模型。

根据物体动平衡原理，船舶静水中平衡方程为：

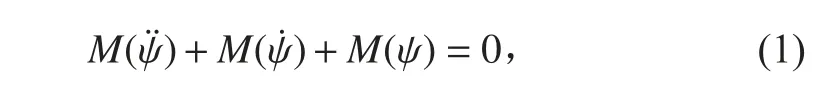
考虑到线性、非线性、正弦方程的影响建立无人艇纵摇运动方程。

辨识方程1：

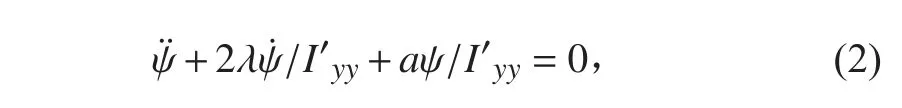
辨识方程2：

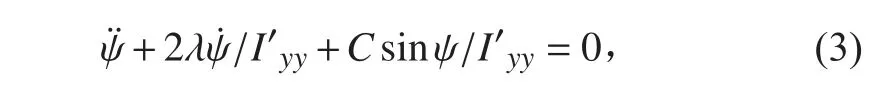
辨识方程3：

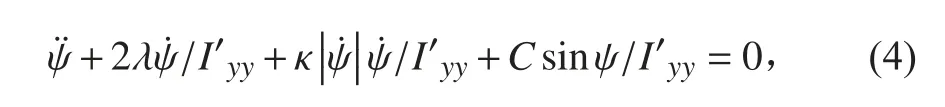
辨识方程4：

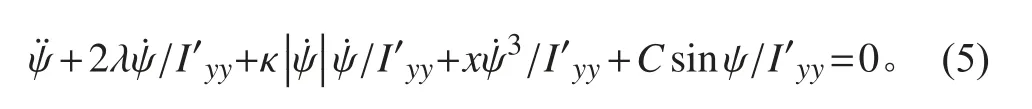
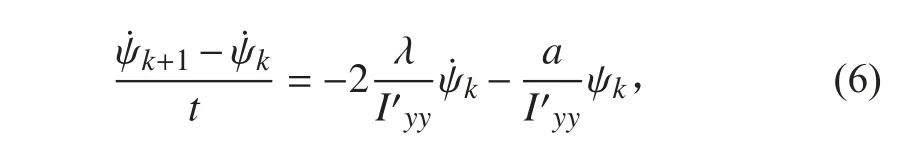
则可对k+1 时刻下的纵摇角速度预报：

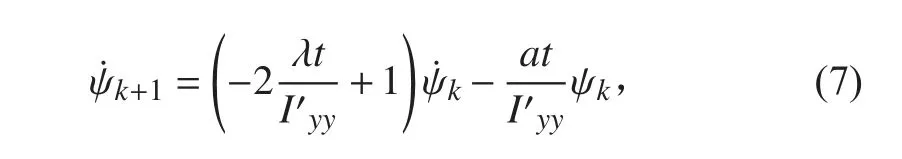
第k+1 时刻的误差估计如下：

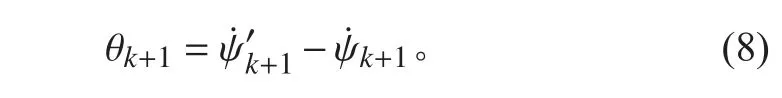
选取目标函数如式（9），该目标函数值越小，表示公式拟合效果越好。

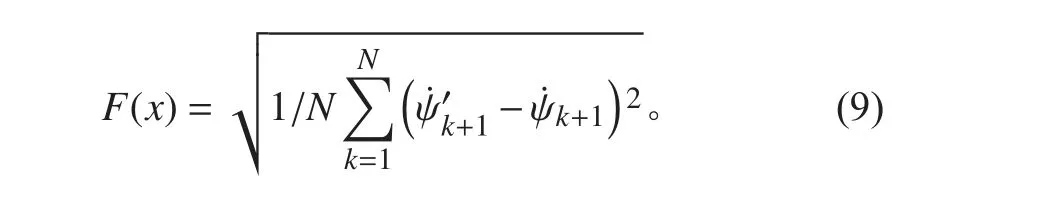
式中：N 为总的采集数据个数。

3 试验与辨识结果分析

3.1 纵摇辨识结果分析

本文选取遗传算法作为系统辨识的基本算法，以2 种不同吃水的纵摇数据进行辨识，比较4 个方程的可靠性，选取一种可靠性较好的辨识方程进行辨识。设置基本参数如下：

种群规模200，变异概率0.05，交叉变异率0.8。在遗传代数为3 000 代分别用4 种辨识方程进行系统辨识，辨识结果如表2 所示。

通过对比上述4 个目标函数值发现，在初始纵摇角为2°，4°，6°的条件下，方程3 的目标函数值最小。由2.2 节可知，目标函数越小，辨识方程的拟合效果越好，因此选用方程3 作为本次试验的辨识方程。

以初始纵摇角度4°时，设计吃水下，方程3 辨识后目标函数值为0.002 123 082 97，各相关参数如表3所示。

代入方程3 得到的辨识方程为：

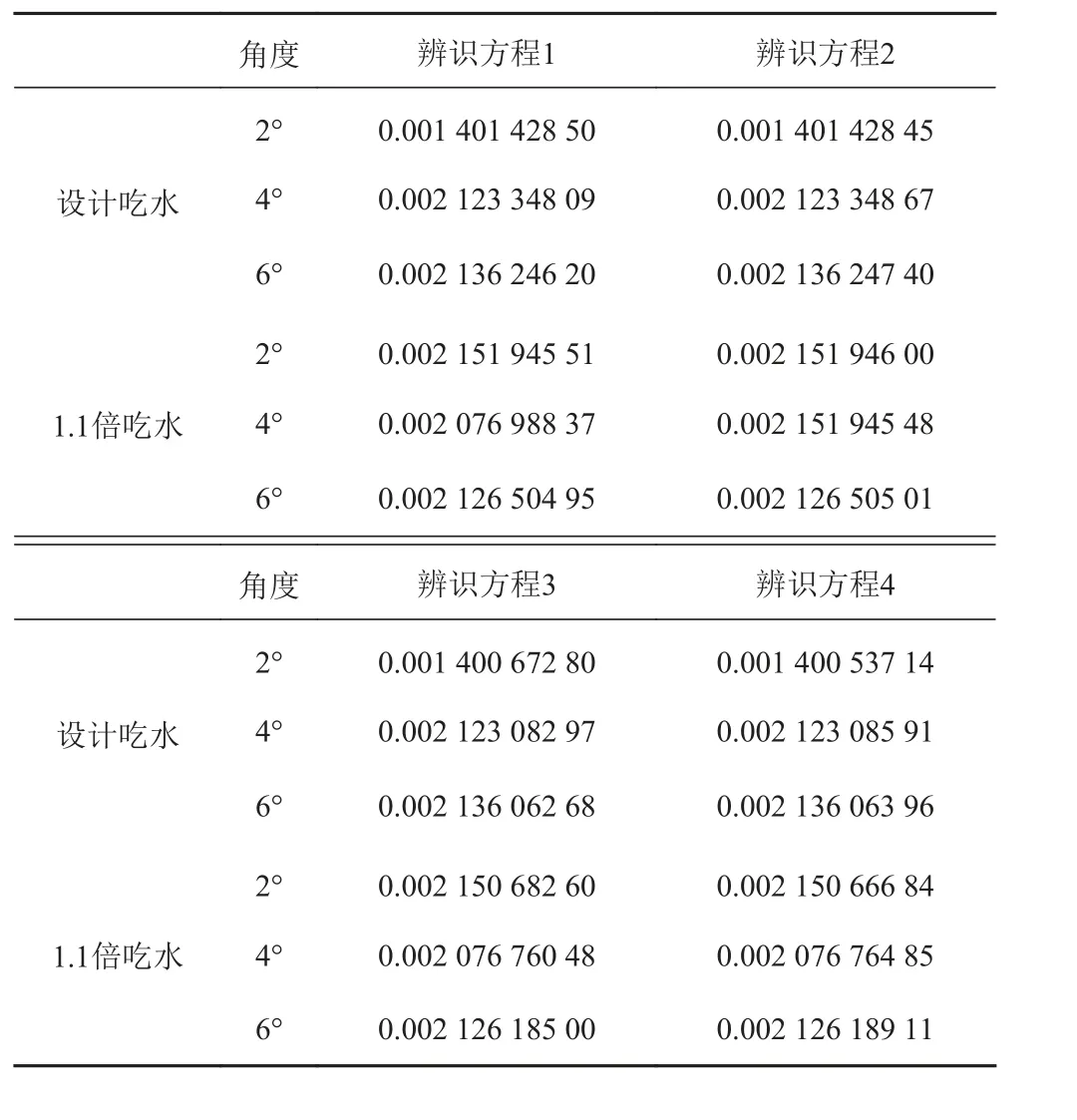
表 2 辨识数学模型的目标函数值Tab.2 Target function values for identifying mathematical models

表 3 方程3 辨识下的各个设计变量优化值Tab.3 Optimal values of design variables identified by equation 3

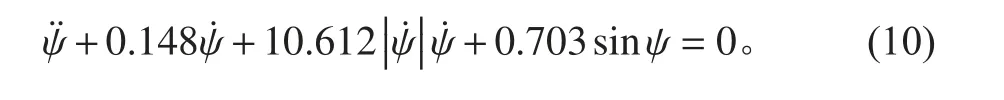
初始纵摇角度4°，遗传代数为3 000 代时，方程3辨识的拟和角速度与试验角速度的对比曲线如图4 所示。

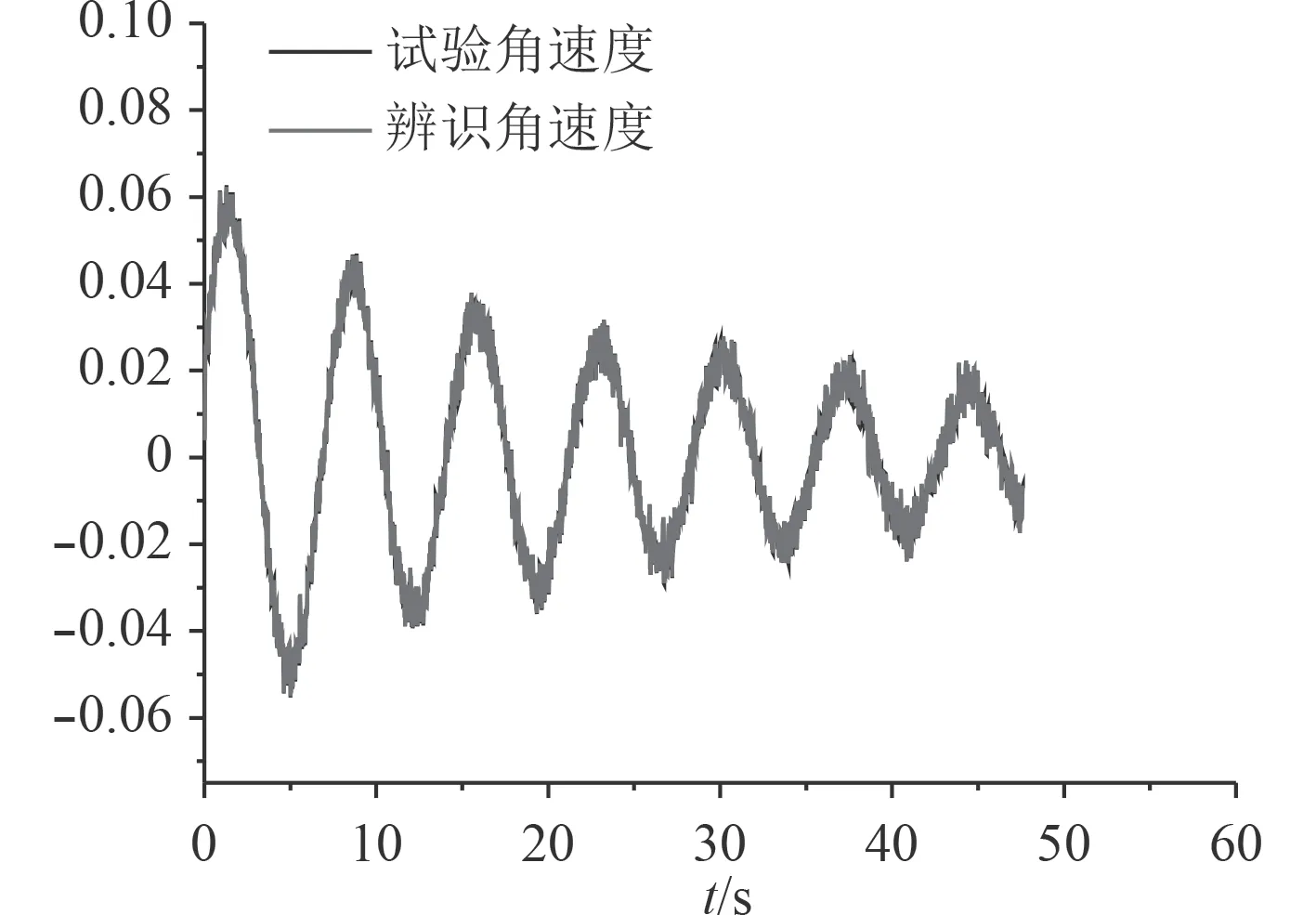
图 4 试验角速度与辨识角速度曲线对比图Fig.4 Comparison of angular velocity curves between test and identification

由图4 可以看出，试验角速度与辨识拟和的角速度变化趋势一致。由表4 可以看出试验角度与辨识角速度的平均误差在4%以内，验证了以方程3 作为辨识模型的准确性且能得到一个较好的结果，还可以预测下一时刻的角速度。

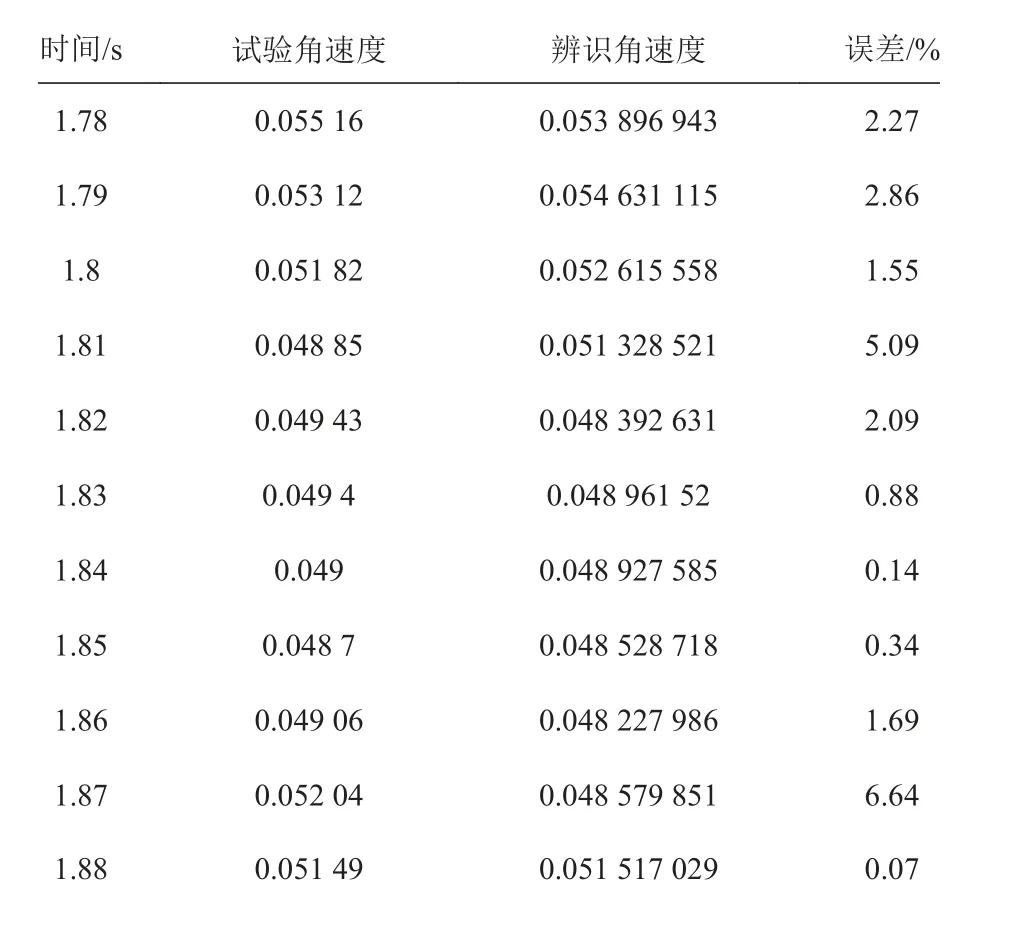
表 4 3 试验与辨识结果误差表Tab.4 Error table of test and identification results

通过方程3 对2 种吃水下的纵摇辨识计算，得到阻尼力矩，复原力矩随时间的变化曲线如图5 所示。

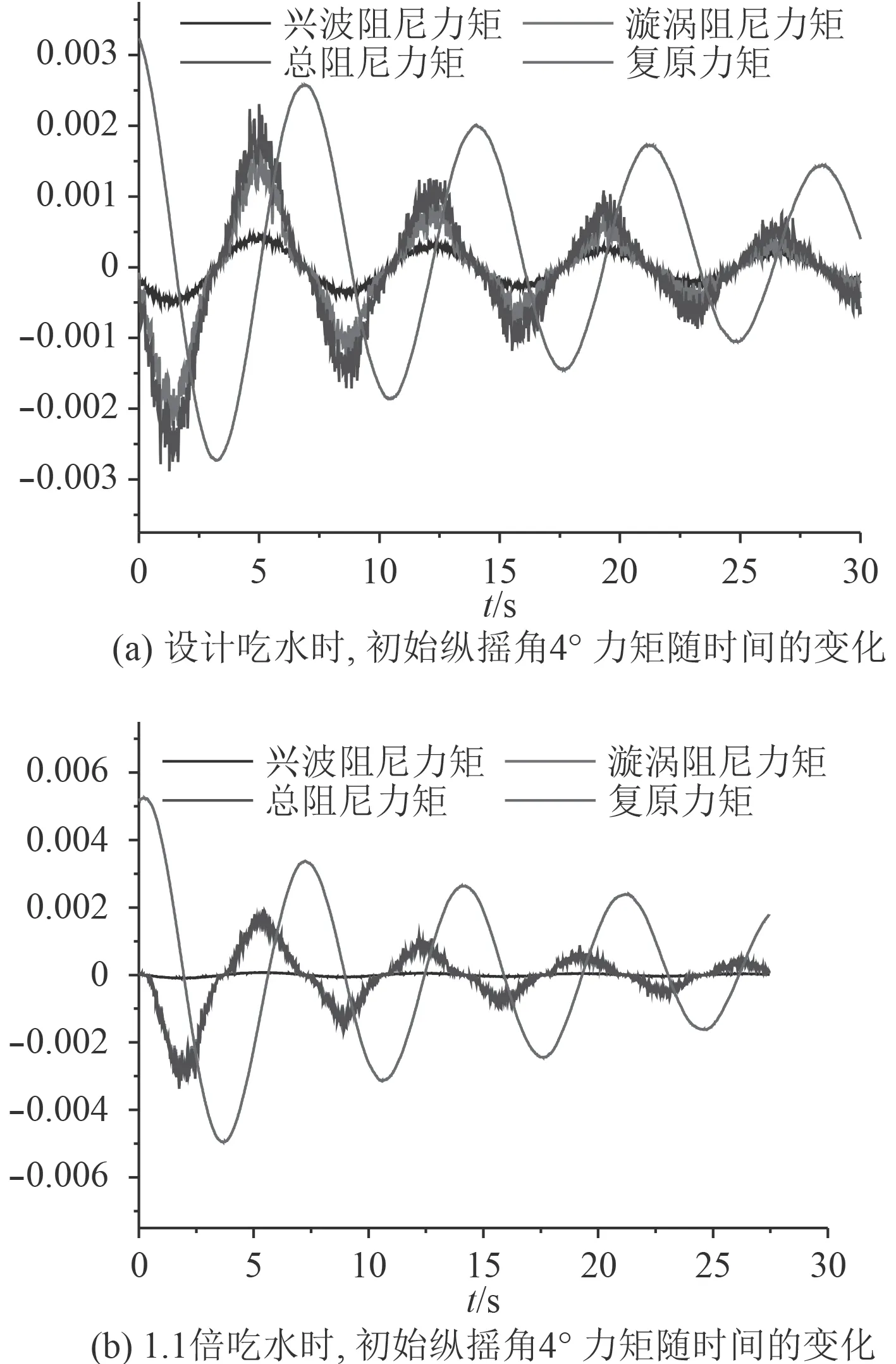
图 5 辨识后纵摇力矩随时间的变化曲线Fig.5 The time-varying curve of pitching moment after identification

由图5 可以看出，艇体各力矩的值随时间的变化，会在一定的区间变化。在总的阻尼力矩中，兴波阻尼对纵摇的影响很小，漩涡阻尼力矩对纵摇产生的影响很大，验证下水线面单体船纵摇运动时，兴波作用影响不大。随着时间的增加纵摇的衰减越来越明显，阻尼力矩和复原力矩变化的幅度越来越小，复原力矩与阻尼力矩峰值相差1/2 个周期。吃水越大衰减周期越短。

4 小水线面复合单体无人艇与同吨位单体滑行艇的纵摇对比分析

本文选取同吨位同种吃水，相同纵摇角4°的单体滑行艇模进行纵摇试验，然后与小水线面复合单体艇模进行对比分析，分析纵摇角速度随时间的变化曲线，如图6 所示。

用辨识方程3，种群规模200，变异概率0.05，交叉变异率0.8，遗传代数为3 000 代的条件下进行系统辨识。得到各力矩系数随时间变化的关系如图7 所示。

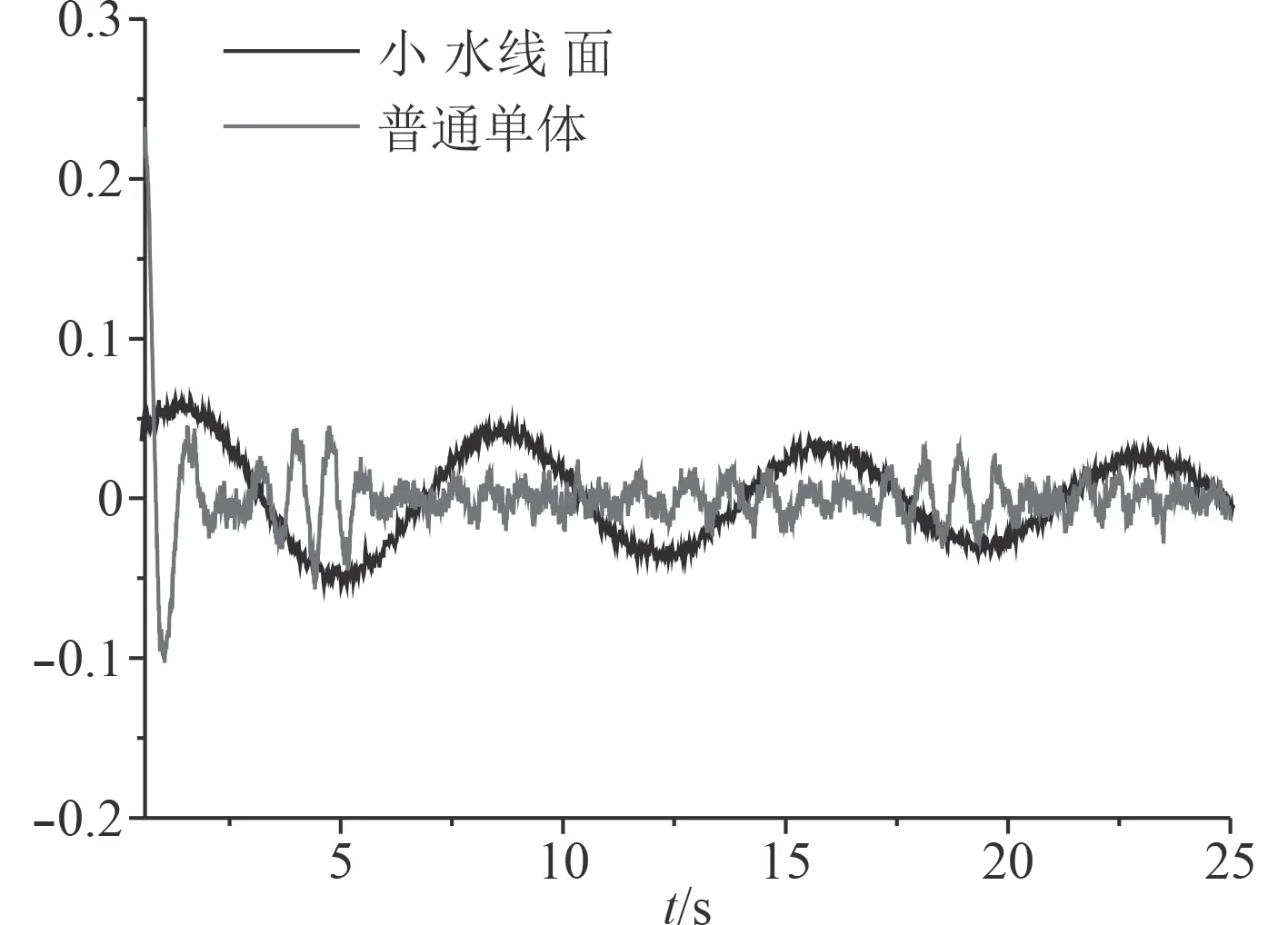
图 6 无人艇初始角4°时两型无人艇角速度随时间的变化曲线Fig.6 Curves of angular velocity of two-type USV with time at initial angle of 4 degree

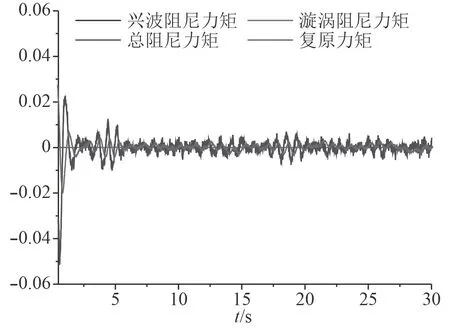
图 7 同吨位单体滑行艇辨识后纵摇力矩随时间的变化曲线Fig.7 Change curve of pitching moment with time for identical tonnage monohull planing craft after identification

由图6 可知，该小水线面复合单体无人艇与同吨位的滑行艇相比，其纵摇衰减周期比较大，约同吨位单体滑行艇的5 倍。由图7 可知，在初始纵摇角为4°纵摇衰减运动时，同吨位单体滑行艇兴波阻尼力矩在阻尼力矩中占的成分很大，是影响纵摇衰减运动的主要因素。验证了同吨位单体无人艇中，小水面复合单体无人艇有较小的兴波性能。

5 结 语

本文通过模型试验和系统辨识方法研究海洋监测单体无人艇的静水纵摇衰减运动模式，建立4 种不同的艇模纵摇模式运动辨识方程，并编入程序，进行程序设计。通过用4 个方程辨识出来的目标函数进行对比，选取可靠性最高的方程3 作为辨识方程进行分析，得到了艇模的静水纵摇数学方程和各个力矩在不同吃水下随纵摇角度的变化规律，与同吨位单体滑行艇纵摇运动模式进行了比较。

小水线面单体无人艇在作纵摇衰减运动时，总阻尼力矩中，漩涡阻尼力矩是影响衰减运动的主要因素，兴波阻尼力矩影响作用很小，同吨位普通单体滑行艇纵摇衰减运动时情况与之相反；纵摇衰减一定时间后，小水线面复合单体船复原力矩峰值和阻尼力矩峰值都是同吨位单体滑行艇的1.5 倍。综上所述，小水线面复合单体无人艇与同吨位普通单体船相比纵摇衰减能力较强。