带权重因子相关函数对数字图像算法性能的影响

王罗斌, 万 强, 韦利明, 岳动华, 贾 东

(中国工程物理研究院 总体工程研究所， 四川 绵阳 621999)

0 引 言

数字图像相关(Digital image correlation,DIC)方法，通过采集物体变形前后的图像，再利用图像算法进行计算，从而得到位移和应变信息.与传统力学测量方法相比，该方法具有以下特点：可实现非接触的全场测量；只需要光学采集系统和控制计算机，对实验环境要求较低；图像采集和处理程序可以固定，容易实现测量自动化[1].此外，该方法与扫描电镜等显微设备相结合，还可在微纳尺度下实现对材料力学性能的测量[2-5].DIC方法的关键是在变形前后的图像中找到最匹配的图像子区，这就需要按照一定的方法进行相关运算和搜索.相关搜索是通过计算变形前后图像子区的相关系数来实现，而相关系数则由相关函数来定义.在传统的相关函数中，图像子区每个像素点对计算结果的贡献是一样的，这与实际情况会有所差别.对此，文献[6]采用带线性权重因子的相关函数来计算变形前后图像子区的相关系数.但该方法线性权重因子函数在计算子区的边缘像素点上的权重取值较低，对边缘区域像素点的影响较大，这可能导致计算结果出现偏差.在此基础上，本研究提出一种带高斯函数权重因子的相关函数，并将其与线性权重因子的相关函数和传统相关函数的计算结果进行了比较，同时，讨论了影响算法计算性能的因素，相关结论可为DIC方法性能的改进和工程应用提供有用参考.

1 数字图像相关方法

1.1 DIC方法基本原理

DIC方法采用摄影机采集物体变形前后的图像，然后通过相关的算法寻找变形前后最匹配的图像子区，从而求得被测物体表面各点的位移.如图1所示，在变形前灰度值分布为f(x,y)的图像(又称参考图像)中，取以某待求点A(x，y)为中心的(2M+1)×(2M+1)像素点计算子区(又称为参考图像子区)，在变形后灰度值分布g(x′,y′)的图像中，通过相关函数计算相关系数，并按照一定的搜索方法，获得相关系数取极值的以A′(x′，y′)为中心的(2M+1)×(2M+1)区域，由此得到了参考图像子区中心点A(x，y)的像素位移(u,v).

图1变形前参考图像与变形后图像子区示意图

1.2 传统相关函数

在对变形前后图像子区进行相关运算前，需先定义它们的相关函数.具体应用时，相关函数的选择主要考虑以下因素：

1)易操作性.相关函数应有简单的数学描述，表达式中的参数便于计算机自动提取，非匹配窗口与匹配窗口的相关函数输出值应有显著差别.

2)抗干扰性.由于受到照明条件等影响，采集到的图像会存在环境噪声，好的相关函数应能够对环境噪声具有较好的抗干扰性，保持稳定输出.

3)较小的计算量.数字图像的像素点多，要求相关函数的形式易于计算，以减少算法的计算量.

目前，常用的效果较好的相关函数有：零均值归一化互相关(Zero-mean normalized cross correlation,ZNCC)函数、零均值归一化最小平方距离(Zero-mean normalized sum of squared differences,ZNSSD)相关函数和参数最小平方距离(Parametric sum of squared difference,PSSDab)相关函数等[7].

ZNCC互相关函数的取值范围为[-1，1].其中，当值为1时，图像为完全相关；当值为-1时，图像为完全不相关.其表达式为，

(1)

ZNSSD互相关函数的取值范围为[0，+∞]，值越小，则图像的相关性越强.其表达式为，

(2)

PSSDab互相关函数的表达式为，

(3)

在式(1)～(3)中，fm、gm分别为变形前后计算子区的灰度平均值.潘兵等[7]对这3种互相关函数进行了等价性证明，推荐使用ZNSSD互相关函数.

1.3 带权重因子的相关函数

传统的相关函数中，图像子区每个像素点对计算结果的贡献是一样的，而这与实际情况有所差别.例如，当图像产生拉伸/压缩变形时，假设图像计算子区中心像素点的位置不变，其余像素点的位置均有变化，且离中心像素点距离越远，其位置变化量(位移)就越大.因此，如果考虑图像子区每个像素点对相关系数的贡献差别，则可引入带权重因子的相关函数.例如，采用ZNSSD互相关函数时，其表达式变为，

(4)

式中，r(x,y)为权重因子函数，其取值仅与点(x,y)在图像计算子区中的位置有关.

考虑如图2所示的变形前参考图像子区和变形后2个图像子区，其中，(a)为变形前的图像子区，(b)和(c)分别为变形后的2个图像子区，u,v分别表示图像在x轴和y轴方向的位移，K、K′分别为图像(b)和(c)中某2个像素特征点.

图2变形前后图像计算子区

考虑一种特殊情况下的状态，假定变形前图像子区(a)中各像素点的灰度值相同，均为s.变形后图像子区(b)和(c)中像素点K和K′的灰度值为k，其余像素点的灰度值为s.

在传统ZNSSD互相关函数中，图像子区(a)与(b)的相关系数表示为，

(5)

式中，x′=x+u1，y′=y+v1.

图像子区(a)与(c)的相关系数表示为，

(6)

式中，x″=x+u2，y″=y+v2.

式(5)和式(6)中，f(x,y)表示图像子区(a)中的灰度值分布，gb(x′,y′)、gc(x″,y″)分别表示图像子区(b)和(c)中的灰度值分布，fm、gbm、gcm分别表示图像子区(a)、(b)和(c)中的灰度平均值，gbm=gcm.

由于f(x,y)=s，故，式(5)和式(6)可以改写为，

(7)

显然有，Cab=Cac.这说明，当采用传统相关函数时，特征点K和K′在不同位置时的2个图像子区不能被区分.

当采用式(4)带权重因子相关函数时，上述2个相关系数分别为，

(8)

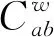
(9)

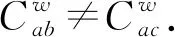
由以上讨论可以看出，当采用传统相关函数时，特征点K和K′在不同位置的2个图像子区不能被区分出，而采用带权重因子的相关函数时，此类问题就能够被解决.

2 计算验证

2.1 计算机散斑图像的生成

研究显示，利用计算机数值模拟的方法，不仅可以生成理想质量的散斑图像，还能避免实际实验中各种噪声的干扰，如光照不均、系统畸变等引起的图像噪声.因此，采用数字模拟散斑图像模拟变形，能够准确评估数字图像算法的计算结果，这也是目前验证和评价数字图像相关算法的通用做法.

针对数字散斑图像的生成，Zhou等[8]提出了一种方法，其基本原理为：在一定大小的图像中，随机生成多个高斯光斑，由多个高斯光斑叠加而成一幅数字散斑图像，其变形前后图像中各像素点的灰度值可以表示为，

(10)

利用式(10)，即可生成一幅数字散斑图像，同时还可以对该图像施加平移或变形.

本研究利用上述方法，得到了一幅计算机仿真散斑图像，具体如图3所示.该散斑图像参数为：图像大小为512×512像素，高斯光斑的半径为4，光斑数目为4 800，中心光强为255灰度值(图像灰度值的范围为0～255).

图3计算所用的数字散斑图像

2.2 带权重因子的相关函数对算法计算性能的影响

文献[8]提出一种线性权重因子函数，其形式为，

(11)

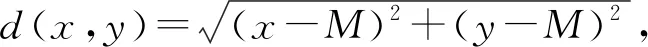
图4图像计算子区示意图

如果采用式(11)来计算图像计算子区中各像素点的权重，其边缘部分像素点所占的权重较小，且4个角点处的权重均为0，这将低估图像边缘区域的像素点尤其是4个角点对相关系数的贡献.对此，本研究提出一种高斯权重因子函数，其形式为，

r(x,y)=e(-d(x,y)2/M2)

(12)

利用式(10)和式(12)，线性权重因子函数和高斯权重因子函数的取值随像素点与图像子区中心点距离d的变化曲线如图5所示.

图5 2种权重因子函数变化趋势比较

2.3 不同相关函数对DIC算法性能的影响

本研究采用曲面拟合法，分别使用传统相关函数、线性权重因子相关函数和高斯权重因子相关函数计算图像在x轴方向逐渐拉伸到应变达20%状态下的位移场，每次增加1%应变.计算子区大小为41×41像素，从图像坐标为(70，70)开始，纵向和横向均是每隔5像素计算一个点的位移值，直到图像坐标为(450，450).本研究共计算5 929个点的位移值，由此得到了该图像下3种计算方法的均值误差绝对值和标准差，并对10幅不同数字散斑图像的计算结果取平均值.通过比较这3种方法的计算结果，由此分析权重因子对DIC算法的影响.

1)在10%拉伸状态下3种方法的计算结果如表1所示.

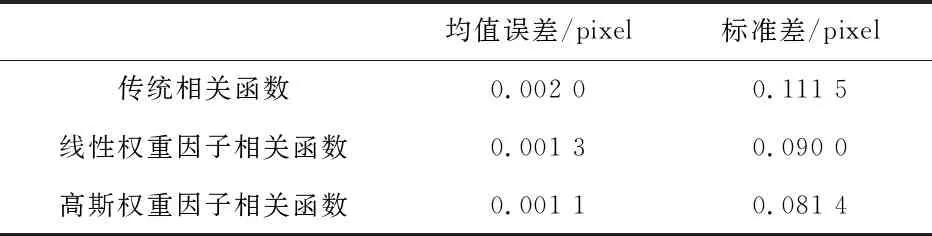
表1 10%拉伸应变下的计算结果比较

从表1可以看出，相比较于传统相关函数，采用线性权重因子相关函数和高斯权重因子相关函数后，曲面拟合法计算结果的均值误差由0.002 0像素点分别减少到0.001 3像素点和0.001 1像素点，标准差由0.111 5像素点分别减少到0.090 0像素点和0.081 4像素点.这表明，2种带权重因子的相关函数均能够有效提高数字图像相关算法的计算精度，而当采用高斯权重因子相关函数的计算方法时，其均值误差和标准差均为最小.

2)在10%拉伸应变下3种方法位移场的计算结果如图6所示，显示图像的大小为60×60像素.

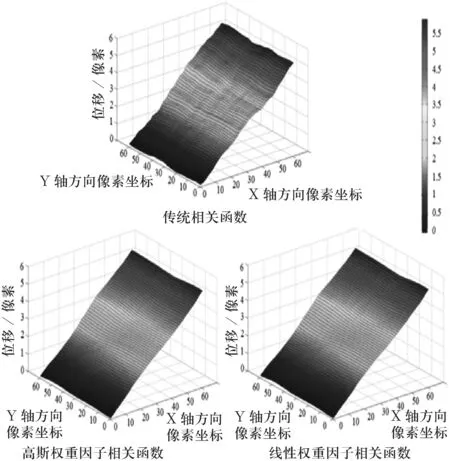
图6 3种相关函数在10%拉伸应变下位移场计算结果

从图6可以看出，由传统相关函数计算得到的位移场变化较大，而采用线性和高斯权重因子的相关函数后，计算得到的位移场平滑性更好.这表明后二者的计算结果更加稳定，计算精度更高.

3)3种方法位移场计算结果的均值误差绝对值和标准差与拉伸应变的关系如图7、图8所示.

从图7与图8中可以看出，采用传统相关函数时，其计算结果的均值误差绝对值和标准差均远远大于另外2种相关函数，且随着拉伸应变的增加，3种相关函数的计算误差增加幅度也越来越大.

总体而言，采用高斯权重因子函数算法的计算精度稍好于线性权重因子相关函数.

图7均值误差绝对值与拉伸应变的关系

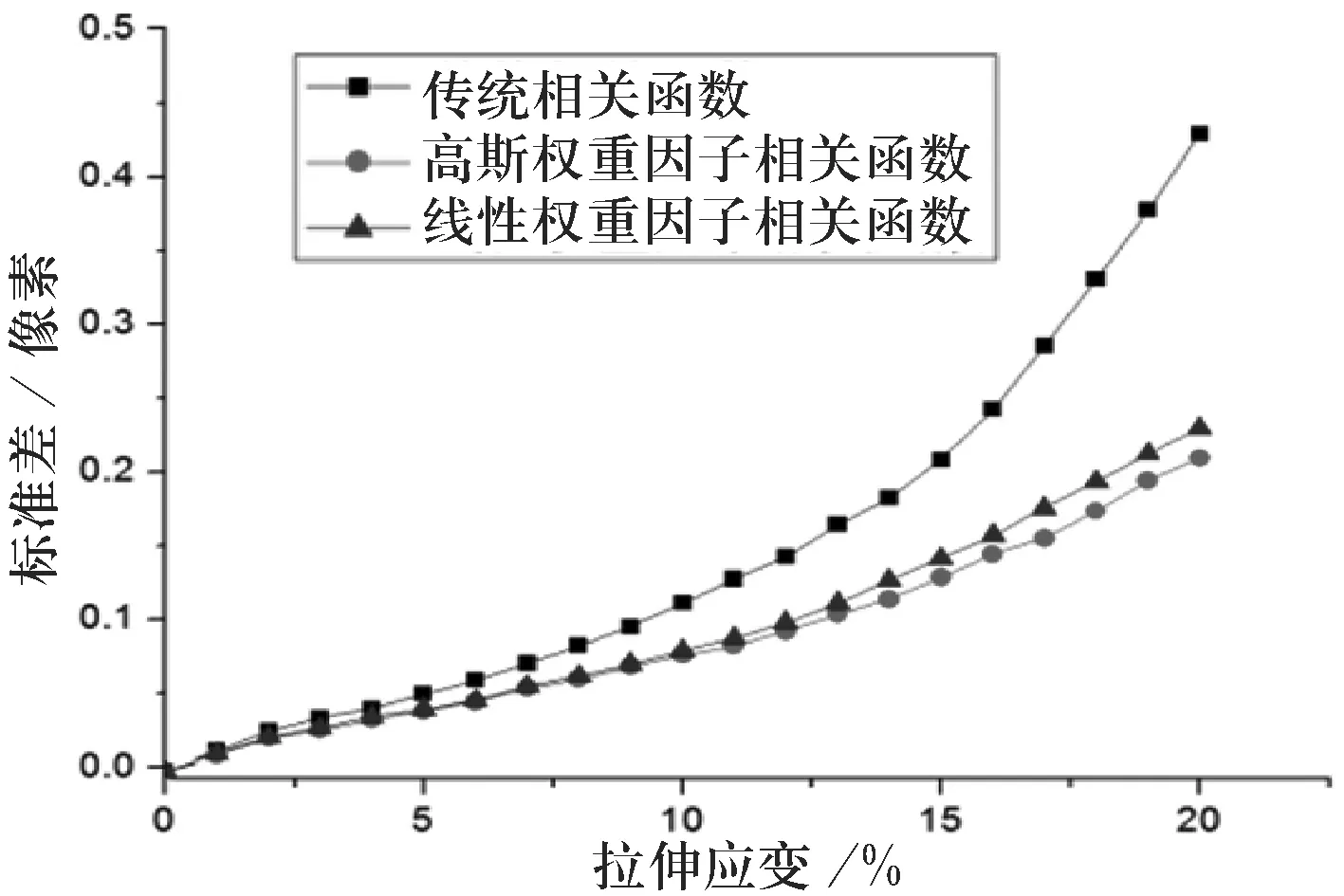
图8标准差与拉伸应变的关系

3 结 语

本研究提出了一种带高斯函数权重因子的相关函数，并将其与线性权重因子的相关函数和传统相关函数的计算结果进行了对比.计算结果表明，相较于传统相关函数，采用线性权重因子相关函数或高斯权重因子相关函数后，数字图像相关算法的均值误差和标准差均有较大幅度下降，这显著提高了算法的计算精度.而当采用高斯权重因子相关函数的计算方法时，其均值误差和标准差均为最小，算法的计算精度较好.

实际上，带权重因子的相关函数，其形式并不只有线性函数或高斯函数，还存在其他函数类型，例如多项式函数.对于每种状态的图像而言，采用哪种类型的相关函数更适合，尚需做更进一步的研究.