数据挖掘诊断X 油田低渗透稠油油藏 压裂效果的主控因素
2020-01-13聂帅帅唐世星徐康泰李江飞王少征
聂帅帅,唐世星,刘 可,徐康泰,李江飞,王少征
(承德石油高等专科学校,河北承德 067000)
水力压裂是低渗透油气藏增产改造的关键技术之一[1]。但是,油气层非均质性强,各井压裂条件参差不齐,使得压裂效果难以保障[2]。因此,如何评价各参数对压裂效果的影响程度,指出制约压裂效果的主控因素,定量优化压裂参数以指导压裂施工,是提高压裂效果的关键所在。
部分学者采用数理统计的方法预测压裂效果。主要分为建立压裂产量的时间序列模型、建立模糊综合评判模型、建立压后产量与压裂影响因素的数学模型3 大类[3-10]。
对压裂效果主控因素诊断尚缺乏较为系统的方法或流程。而当前数据挖掘、大数据等技术的兴起,为决策优化类问题提供了一种新的研究手段或研究角度。为此,本文基于当前较为成熟的R 语言数据挖掘平台,在建模参数筛选和数据标准化的基础上,建立压后产量与压裂参数间的最优数学模型,从而 实现压裂效果的预测、压裂效果主控参数的诊断和优化,达到定量指导压裂方案优化的目的。
X 油田储层孔隙度为9%~21%,渗透率多低于50 ×10-3μm2,50 ℃时原油黏度119~455 mPa·s,原始平均压力系数为0.93,自然条件下平均单井日产油为1 t,是典型的低压、低渗、低产、稠油油藏。因此,水力压裂是提高该油田开发效果的关键。该油田采用活性水压裂液,压裂后日产油低于15 t,压裂井的压裂效果差别较大。
1 参数筛选
根据石油天然气行业标准SY/T5289-2008《油、气、水井压裂设计与施工及效果评估方法》,采用压裂后一个月的平均日产油量来评估压裂效果。
共采集X 油田52 口井的压裂数据,参数15个,包括孔隙度Φ、渗透率K、含水饱和度Sw、压裂厚度h、加砂量VS、平均砂比Sb、前置液量Vpad、携砂液量Vscl、实际压裂液量Vinj、反排量Vffr、反排率η、破裂压力Pf、停泵压力Ps、放喷压力Pa、日均产油量q。由于各压裂参数之间存在着一定的数学关系,在建立数学模型时,应先剔除共线参数,保证建模参数之间的独立性。
1.1 相关性系数确定强相关参数
Pearson 相关性分析可以衡量两两变量之间的线性相关性大小[11],计算公式如下:
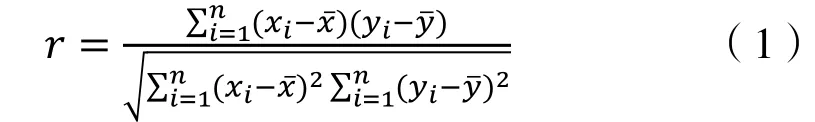
式中:r为相关系数,无量纲;x、y为变量,这里指孔隙度Φ、渗透率K 等15个参数;n为观测井数。
如果相关系数r≥0.8,表示相关程度高;如果0.6≤r<0.8,表示相关程度中等;如果r<0.6,表示相关程度低。
1.2 方差膨胀因子检验多重共线参数
统计Vif(Variance Inflation Factor,方差膨胀因子)是检测因素是否共线的指标[12]。表征了参数的置信区间能膨胀为与模型无关的自变量的程度。一般认为当时,因素共线。
直接建立q 与14个参数间的回归模型,采用统计Vif 检验多重共线性,结果如图1。
从图1 可以看出,Sb、Vs、Vpad、Vscl、Vinj、Vffr、η、Ps和Pa等9个参数之间存在多重共线性,检测结果与相关性分析的结果一致。
为避免因素多重共线,Vs、Vpad、Vscl、Vinj等4个参数选择1个即可,这里选取与q 相关性最大的Vpad;Vffr和η 等2个参数选择1个即可,在已选择Vpad的前提下,选择η;Ps和Pa等2个参数选择1个即可,这里选择Ps。因此,共剔除Vs、Vscl、Vinj、Vffr和Pa等5个参数。

图1 多重共线检验
再次拟合q 与剩余9个参数回归模型,诊断参数是否存在多重共线性发现,所有参数均通过检验,不存在多重共线性。因此,已经成功剔除共线参数,下一步可以建立模型。
2 数学模型建立
由于每口井的资料难以保证是用同一类仪器、相同刻度标准化及统一操作方式而测得,且不同参数的量纲和数量级差别也较大,为消除这种影响,采用min-max 方法对原数据标准化,将变量的取值范围映射到[0,1]区间,再建立数学模型。min-max标准化计算公式如下:

式中:x*为标准化后的变量数值,无量纲;x为变量的原始观测值;xmax为变量x的最大观测值;xmin为变量x的最小观测值。
数据标准化后直接建立压后产量与剩余9个参数回归模型发现,Ra2=0.15,拟合度低,且9个参数均未通过显著性检验,模型较差,需要进一步优化。
2.1 模型优化
采用全子集回归方法确定最佳自变量组合[13]。全子集回归就是在检验所有可能模型的基础上,找出最佳模型。全子集回归发现Ra2最高仅为0.24,模型拟合效果依旧不理想。说明存在异常数据难以拟合模型,需要剔除异常值。
异常值包括离群点、高杠杆值点和强影响点等3 种类型。离群点是指拟合效果不佳的点,他们往往残差较大;高杠杆值点是与其他预测变量有关的离群点,可用帽子统计量(Hat-Values)判断。帽子统计量为模型参数的数目P 与样本量n 的比值。一般认为,观测点的帽子值大于帽子均值的2 倍以上,即为高杠杆值点;强影响点是指对参数估计值影响有些比例失衡的点,常采用距离库克(Cook)的距离,即D 统计量检测强影响点;当D 值大于4/(nk-1)时,即认为是强影响点,其中,k 是预测变量数目,为1。将离群点、高杠杆值点和强影响点整合到一张图中,如图3 所示。图中纵坐标超过+2 或-2的点为离群点,水平轴虚线以外的点为高杠杆值点,圆圈大小代表着影响程度,圆圈越大,对模型参数估计的影响就越大。
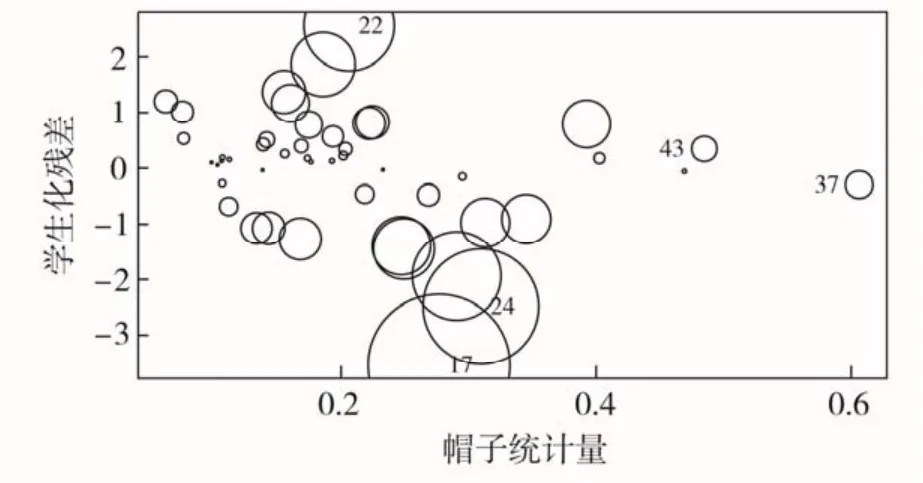
图2 异常值观测
从图2 可以看出,17#井、22#井和24#井是3个圆圈最大的点,影响程度最大。同时,这3个数据也属于离群点,优先删除这3个观测。删除后再次采用全子集回归,Ra2=0.61,说明剔除异常值后能显著提高模型的拟合度。同时,拟合度在0.60 以上的模型参数组合达到14个。
当面对多个模型时,有的模型拟合好,有的模型预测能力强,一般采用AIC 值(Akaike Information Criterion,赤池信息准则)优选出最佳模型,是综合考虑了模型的拟合度和参数数目,力求用最少的参数获取足够的拟合度[14]。
计算14个模型的AIC 值发现,当模型参数组合为K、h、Vpad、η 和Pf时,AIC 值最小为-37.93,初步认为是最优模型。但是,常数项(P=0.56)和Pf项(P=0.11)未通过显著性检验。进一步去除常数项和Pf项,再次拟合Ra2=0.95,参数均通过显著性检验。且AIC 降低至-38.27,模型更优。
综上,建立的最优数学模型如下:

式中:q*为标准化的压裂后一个月平均日产油量,无量纲;K*为标准化的渗透率,无量纲;h*为标准化的储层厚度,无量纲;V*pad为标准化的前置液量,无量纲;η*为标准化的返排率,无量纲。
2.2 模型诊断
为了检验模型的合理性,进行回归诊断,结果如图3 所示。从图3 可以看出,图3a 的残差拟合图上的数据点呈随机分布,说明模型整体符合线性假设;图3b 的正态Q-Q 图上的数据点分布在45°角直线上,说明模型符合正态性假设。图3c 的位置尺度图的数据点呈随机分布,说明模型满足不变方差假设;图3d 的残差杠杆图显示所有观测井的库克距离均在0.5 以内,说明数据中不存在异常值。因此,回归模型满足线性、正态性、不变方差假设,且不存在异常值,模型合理。

图3 回归诊断
模型整体上是满足线性假设的,但是还需进一步检验各自变量与因变量是否完全满足线性假设。绘制了q 与K、h、Vpad、η 等4个参数的成分残差图(Component + Residual Plots),如图4 所示。图4a的成分残差图显示的渗透率K 与日均产油量q 的局部拟合线(实线)和从日均产油量q 方向上侧面看过去的多元最小二乘回归平面(虚线)基本重合,且实线和虚线均为线性,表明渗透率K 与日均产油量q 满足线性关系;同样的,图4b 的成分残差图表明储层厚度h 与日均产油量q 成线性关系,图4c 的成分残差图表明前置液量Vpad与日均产油量q 成线性关系,图4d 的成分残差图表明返排率η 与日均产油量q 成线性关系。因此,K、h、Vpad、η 等4个自变量与因变量q 均满足线性假设。

图4 成分残差图
为判断q 值(或残差)是否相互独立,进行误差独立性检验(Durbin-Watson)发现,P 值不显著(P=0.72),误差项之间独立。
最后,对线性回归模型假设进行综合验证,包括偏斜度、峰度等。检验结果表明,多元回归模型满足所有假设统计(P=0.76)。
3 结果分析
基于建立的数学模型,实现压裂效果预测、主控参数诊断和优化。
3.1 压裂效果预测
将5 口预测井数据代入多元回归模型,得到日产油量预测结果见表1。从表1 可以看出,5 口井预测平均准确度86.19%,预测准确度能够满足工程需求。
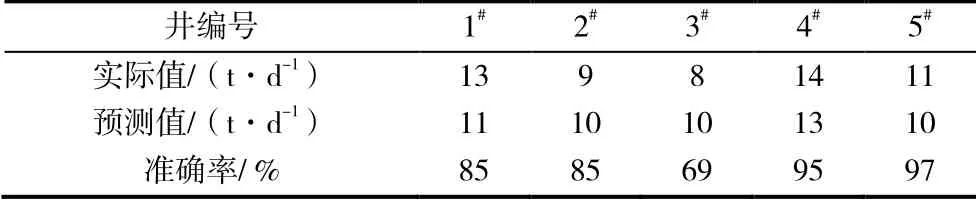
表1 回归模型预测结果
3.2 主控参数诊断
回归系数可以衡量各参数对产量的影响程度,回归系数的绝对值越大,说明自变量对因变量的影响程度越大。除了用回归系数寻找主控因素外,还可以用相对权重来衡量各自变量对因变量的影响程度,即对所有可能的子模型添加1个自变量引起R2平均增加量的一个近似值[15]。
各参数回归系数和相对权重对比如图5 所示。从图5 中的回归系数可以看出,返排率的回归系数最大,为0.89,其次是前置液量,为0.44;从相对权重上可以看出,返排率的相对权重最大,为0.46,其次是前置液量,为0.37。因此,无论是看回归系数,还是看相对权重,返排率是影响压裂效果的主控因素,其次为前置液量。提高压裂规模可以进一步改善储层,而提高压裂液返排率可以进一步降低储层伤害程度,诊断结果与实际情况相吻合。
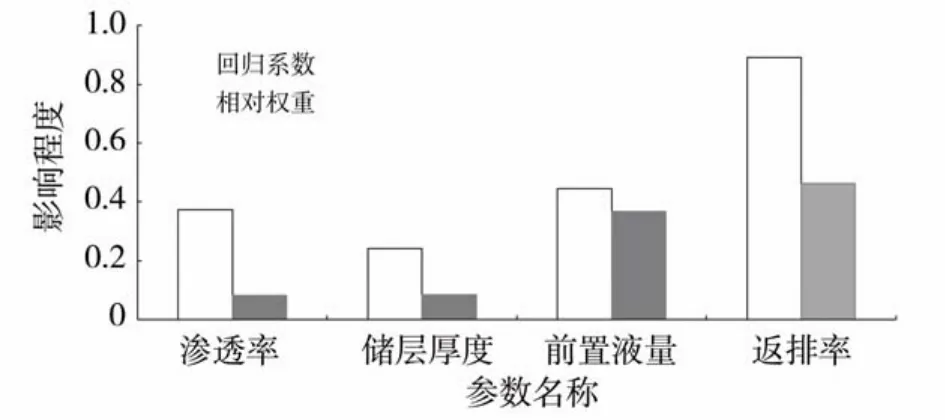
图5 模型参数相对权重
3.3 主控参数优化
31#井日产油1.7 t,压裂效果最差。以该井为例优化施工参数。已知K=2.99×10-3μm2,h=21.7 m,代入式(3)得到Vpad、与q 的关系,如图6 所示。从图中可以看出,对于给定的q 值,可以从图中直接找到对应的Vpad和η 的取值。
4 结论
(1)基于多种数据挖掘方法分析压裂数据,建立压后产量与压裂参数间的最优数学模型,能够实现压裂效果的预测、主控参数的诊断和优化,为油田压裂现场施工提供定量化指导。
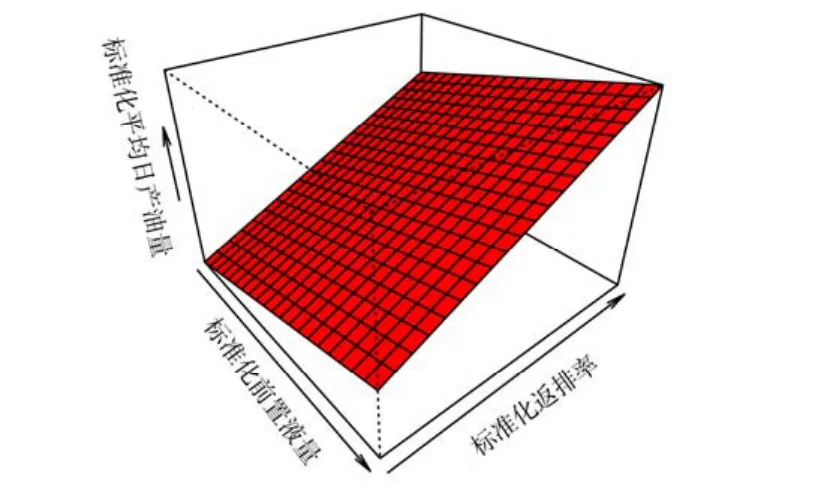
图6 压裂参数与产量的关系
(2)诊断结果表明,X 油田压裂效果主控因素为返排率,其次为压裂液量。因此,为提高X 油田压裂效果,应该从提高压裂规模和返排率入手。提高压裂规模可以进一步改善储层,而提高压裂液返排率可以进一步降低储层伤害程度,诊断结果与实际情况相吻合,具有一定的理论指导价值。
(3)从数据角度寻找产量主控因素是一种新的研究方式,未来还需进一步与大数据、机器学习等方法相结合,从各方面挖掘油气数据的潜在价值,实现油气开发的智慧化。
