收缩徐变对装配式混凝土叠合梁挠度的影响

唐迪未，金伟良，毛江鸿，赵羽习，方言

(1. 浙江大学 建筑工程学院，杭州 310012；2. 浙江大学宁波理工学院，浙江 宁波 315100)

装配式混凝土结构是指预制混凝土构件通过可靠的连接方式装配而成的混凝土结构[1]，具有提高工程质量、减少现场施工作业、减少环境污染等优点[2]。混凝土叠合梁是装配式混凝土结构中的主要构件形式，是预制混凝土梁顶部在现场后浇混凝土而形成的整体受弯构件[1]。混凝土叠合梁中现浇和预制混凝土的龄期和强度存在差异，会在现浇和预制混凝土之间存在收缩徐变微差[3]。收缩徐变微差会造成现浇和预制混凝土之间有微差应力并进一步增大混凝土叠合梁的挠度，从而影响构件的力学性能。

综上所述，收缩徐变作用下装配式混凝土叠合梁挠度的计算以有限单元法和求解微分方程组为主，其计算过程复杂，不便应用。本文基于平均曲率法[3]建立了装配式混凝土叠合梁挠度计算方法，将该方法与数值模拟进行了比较，并结合工程应用分析了预制混凝土加载龄期、叠合面处应力水平对挠度的影响规律。

1 考虑收缩徐变作用的混凝土叠合梁挠度计算方法

1.1 基本假定

混凝土叠合梁常用截面形式如图1所示。中国相关规范[15]中考虑长期作用对挠度增大的影响时推荐了欧洲CEB-FIP[16]、美国ACI[17]等规范推荐的计算方法，在装配式混凝土叠合梁的挠度计算和有限元分析时，采用CEB-FIP MC90模型，并引入如下假定：

2)钢筋混凝土构件是由钢筋和混凝土两种材料组成，将钢筋换算为等效混凝土，换算时钢筋的重心位置与换算后等效混凝土的重心位置一致，换算后的受力效果不变。

3)由于叠合梁的翼缘刚度相对腹板刚度较小，翼缘处预制和现浇混凝土之间的收缩徐变微差对梁的挠度影响较小，忽略其影响，将翼缘预制混凝土等效代换为现浇混凝土。

图1 叠合梁截面形式Fig.1 Composite beam cross

1.2 挠度组成

在收缩徐变的作用下混凝土叠合梁挠度会随着时间而增加，其挠度可表示为

w=w0+w1+w2

(1)

式中：w0是加荷瞬间叠合梁的初始挠度，即没有收缩徐变作用下的挠度；w1是初始挠度在徐变作用下增加的挠度，如图2所示；w2是预制和现浇混凝土叠合面处的收缩徐变微差而引起的挠度，如图3所示。

图2 徐变作用下预制和现浇混凝土的挠度演化过程Fig.2 Deflection evolution process of precast and cast-in-place concrete under the action of

1.3 徐变作用下荷载挠度的变化值

荷载作用下混凝土叠合梁会产生初始挠度w0，徐变作用下该挠度会增加，挠度演化过程如图2所示，叠合前，预制混凝土产生挠度值为φpw0，现浇混凝土产生挠度值为φcw0，当预制和现浇混凝土叠合后，两者共同变形产生挠度w1。由于抗弯刚度越大，变形越小，预制和现浇混凝土叠合时各自产生的变形量与抗弯刚度成反比，因此，叠合时预制混凝土产生如式(2)所示变形。

(2)

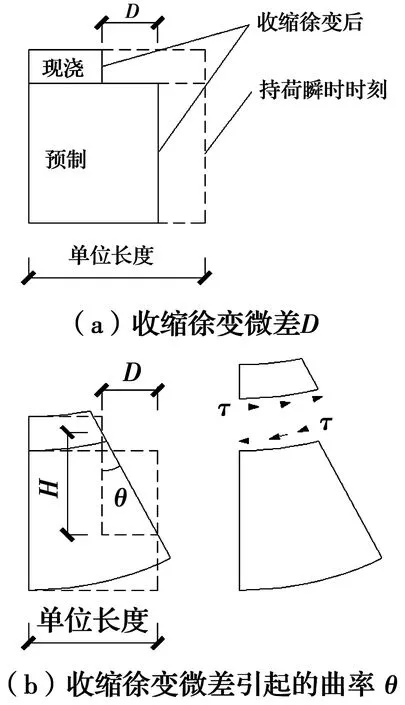
图3 收缩徐变微差及其引起的曲率Fig.3 Differential shrinkage and creep and the

预制混凝土叠合时产生的变形wp加上φpw0即得混凝土叠合梁的初始挠度在徐变作用下增加的挠度w1。

(3)

式中：φp为预制混凝土的徐变系数；φc表示现浇混凝土徐变系数；E1I1表示等效代换后现浇混凝土的抗弯刚度；E2I2表示等效代换后预制混凝土的抗弯刚度。

1.4 收缩徐变微差引起的挠度

收缩徐变微差的定义如图3所示，预制混凝土和现浇混凝土持荷时会在叠合面处产生相同变形，由于预制和现浇混凝土的混凝土强度等级和加载龄期不同，产生的收缩徐变应变不同，其差值为收缩徐变微差D。

沿梁长取一单位长度微段如图3所示，由于现浇和预制混凝土之间存在收缩徐变微差D，为了满足变形协调条件，在叠合面处会产生剪应力，并在横截面之间会产生一微小角度θ，θ即为该单位微段的曲率。依据材料力学中梁的挠度和跨中曲率的关系，D引起的挠度与混凝土叠合梁跨中处θ的关系为

w2=(αθc+0.125θs)L2

(4)

θc=Dc/H

(5)

θs=Ds/H

(6)

Dc=(φcc(t)-φpc(t))ε0

(7)

Ds=(εcsh(t)-εcsh(t0))-(εpsh(t)-εpsh(t0))

(8)

式中：θc为跨中截面处徐变微差引起的曲率；α与荷载形式相关，三分点加载时α为23/216；θs为跨中截面处收缩微差引起的曲率；Dc为跨中截面徐变微差；Ds为跨中截面收缩微差；H为预制混凝土和现浇混凝土微差应力中性轴之间距离，可通过平均曲率法[3]计算；L为跨度；φcc(t)为计算时刻现浇混凝土徐变系数；φpc(t)为计算时刻预制混凝土徐变系数；ε0为跨中叠合面处初始应变；εcsh(t)为计算时刻现浇混凝土收缩应变；εpsh(t)为加载时刻现浇混凝土收缩应变；εpsh(t0)为计算时刻预制凝土收缩应变，为加载时刻预制混凝土收缩应变。

2 考虑收缩徐变作用的混凝土叠合梁挠度数值模拟

2.1 数值模拟

(9)

式中：Δεc(t)为徐变应变增量；Δφ(t)为徐变系数增量。混凝土徐变本构模型编程时采用向前差分法[19]逼近徐变本构曲线，湿度取65%，根据图5所示梁截面尺寸C35混凝土翼板处构件理论厚度取113.33 mm，C30混凝土翼缘处构件理论厚度取80 mm，腹板处构件理论厚度取133.33 mm。

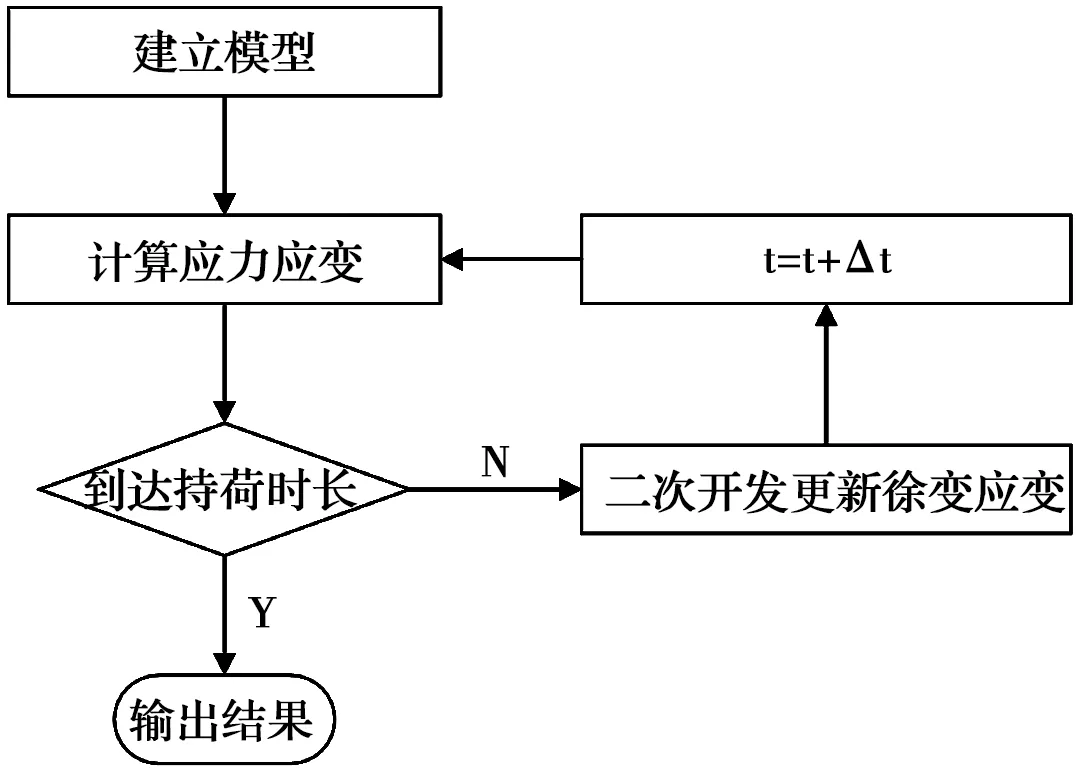
图4 二次开发流程图Fig.4 Secondary development flow

收缩应变模拟时用温度应变来等效，采用温度和混凝土线膨胀系数共同随时间变化的方法。整个混凝土叠合梁区域设置与时间成正比关系的温度场，每一个温度点的线膨胀系数值采用式(10)计算

(10)

式中：εsh(t0)为加载时刻的收缩应变；εsh(t)为计算时刻的收缩应变；T表示温度。只要温度点取得足够密，即可模拟出混凝土随时间收缩的过程。

梁截面尺寸与配筋如图5所示，保护层厚度25 mm，梁长2 000 mm，采用三分点加载，三分点处荷载各为10 kN，三分点间距600 mm，采用solid 186单元模拟混凝土，link 8单元模拟钢筋，两种混凝土之间不产生滑移，钢筋和混凝土之间不产生滑移，混凝土容重为24 kN/mm3,在梁底距离端部100 mm的支座处采用线约束，一端为固定铰支座，一端为滑动铰支座，梁采用映射网格，梁和钢筋的网格宽度均为5 mm。有限元模型如图6所示，模拟所得应力云图如图7所示。

图5 叠合梁截面尺寸与配筋Fig.5 Section size and reinforcement of composite

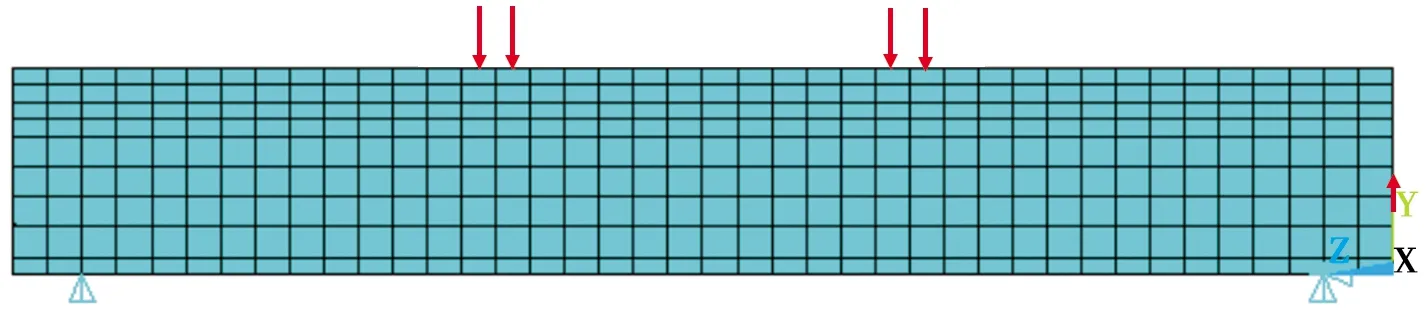
图6 混凝土叠合梁支座和荷载布置图Fig.6 Supports and load arrangement of concrete

图7 混凝土叠合梁模拟应力图Fig.7 Simulation stress of concrete composite

2.2 数值模拟和理论计算的对比

用式(11)计算的徐变挠度系数进行结果对比。

(11)

采用平均曲率法计算式(11)中各系数，混凝土叠合梁的截面特征参数如表1所示。

表1 混凝土叠合梁截面特征参数Table 1 Characteristic parameters of cross section of concrete composite beams

代入式(3)和式(4)，得

w1=(0.764φp+0.236φc)w0

(12)

w2=(23θc/2 156+0.125θs)L2

(13)

现浇和预制混凝土的加载龄期设置如下：现浇混凝土的加载龄期为28 d，考虑到预制混凝土比现浇混凝土至少提前浇筑一个月，由于施工现场进度的不确定性，预制混凝土加载龄期分别取68、98、128、158 d。计算结果和数值模拟结果的对比如图8所示。持载365 d时，预制混凝土加载龄期为68、98、128、158 d时，计算值和模拟值的误差分别为1%、7%、10%、13%，与模拟值相比，计算值偏大，且误差随着预制混凝土加载龄期的增大而增大，这是因为数值模拟时钢筋对混凝土徐变应变的约束作用使变形减小，而理论计算时，假设式(2)中把钢筋等效换算为混凝土时会忽略钢筋对混凝土徐变应变的约束作用。

图8 计算结果与模拟结果对比图Fig.8 Comparisons between calculated results

通过理论计算与数值模拟的对比发现，计算值比模拟值偏大，但对于工程应用而言，其差值在允许范围内且偏安全，此外，对于工程应用而言，理论计算方法更为简单方便。下面研究收缩徐变作用下混凝土叠合梁挠度计算方法的工程应用。

3 工程应用研究

基于计算公式分析预制混凝土加载龄期、预制混凝土跨中叠合面处截面初始应力对装配式混凝土叠合梁挠度的影响规律，为便于称呼，将预制混凝土跨中叠合面处截面初始应力称为叠合面处设计应力。算例叠合梁的基本参数与上文相同。

3.1 预制混凝土加载龄期、叠合面处设计应力对收缩微差和徐变微差的影响分析

改变预制混凝土的加载龄期，根据式(7)、式(8)计算现浇和预制混凝土的徐变微差和收缩微差，结果如图9所示。图9 (a)、(b)中表明徐变微差和收缩微差都会随着预制混凝土加载龄期的增大而增大，但收缩微差的值比徐变微差大一个量级。同时改变预制混凝土加载龄期和叠合面处设计应力，如图9 (c)所示，收缩微差不随叠合面处设计应力变化，徐变微差随着叠合面处设计应力的增大而增大，且徐变微差相较收缩微差较小。在弹性工作阶段，混凝土叠合梁叠合面处应力不会大于预制混凝土的开裂应力，预制混凝土加载龄期365 d且持荷365 d时，收缩微差与徐变微差基本达到最大值，所以，图9包含了混凝土叠合梁叠合面处设计应力、徐变微差与收缩微差的基本情况。其中，徐变微差与收缩微差的最大比值为0.183，表明徐变微差相对收缩微差较小，当跨中叠合面处设计应力很小时，混凝土叠合梁挠度计算时可以忽略徐变微差的影响。

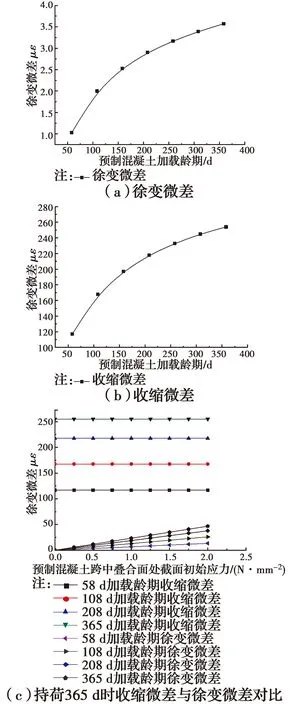
图9 收缩微差与徐变微差的对比Fig.9 Comparison of differential shrinkage

3.2 预制混凝土加载龄期和叠合面处设计应力对挠度的影响分析

由图8可知，计算结果和模拟结果中叠合梁的徐变系数都随着预制混凝土加载龄期的增大而增大。基于装配式混凝土叠合梁挠度计算方法，对加载龄期与叠合面处设计应力进行敏感性分析。令现浇混凝土加载龄期不变，改变预制混凝土加载龄期和叠合面处设计应力，结果如图10所示。σ0为表1情况下叠合面处设计应力，σ为不同荷载下叠合面处设计应力。图10(a)～(c)中w1随着预制混凝土加载龄期的增大而减小，这是因为ψc随着预制混凝土加载龄期的增大而减小，而现浇混凝土加载龄期不变φp不变；w2随着预制混凝土加载龄期的增大而增大，这是因为D会随着预制和现浇混凝土加载龄期差值的增大而增大。图10(a)中，w1与w2之和随着预制混凝土加载龄期的增大而增大，图10(b)中，w1与w2之和几乎不随预制混凝土加载龄期变化，图10(c)中，w1与w2之和随着预制混凝土加载龄期的增大而减小，这是因为混凝土叠合梁初始挠度在徐变作用下增加的挠度w1受应力影响大，收缩徐变微差引起的挠度w2受应力影响小，所以，在不同应力水平下，挠度随加载龄期变化呈现不同趋势。

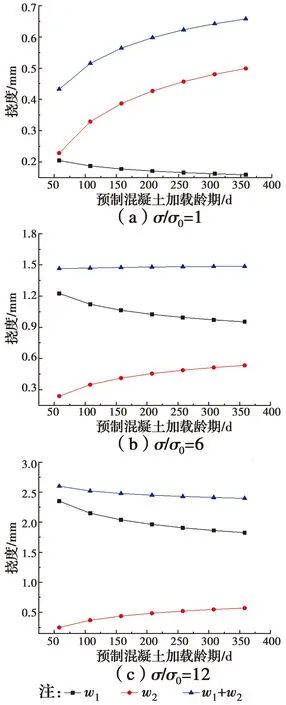
图10 持载365 d时预制混凝土不同加载龄期下的挠度Fig.10 Deflection under different loading age of precast concrete age at 365

预制混凝土加载龄期为58、358 d时的w1不相同，令其差值为Δw1，同理，预制混凝土加载龄期为58、358 d时的w2不相同，令其差值的为Δw2，不同应力水平下Δw1和Δw2的关系如图11所示。Δw1随加载龄期增大而减小，Δw2几乎不随加载龄期变化；当σ/σ0小于6.25时，Δw2的影响更大，当σ/σ0大于6.25时，Δw1的影响更大，说明当σ/σ0小于6.25时，挠度随加载龄期增大而增大，当σ/σ0大于6.25时，挠度随加载龄期增大而减小。

将应力水平、预制混凝土加载龄期与挠度增加值w1+w2的关系绘制成表2，表中规律与图11一致。工程应用时，可计算不同应力下挠度增加值与预制混凝土加载龄期的关系，在装配式结构施工时，选择合适的装配时机以减小收缩徐变微差对挠度的影响。

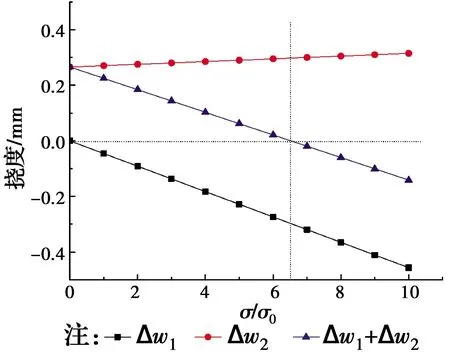
图11 不同应力水平下的挠度变化Fig.11 Change of deflection at different stress

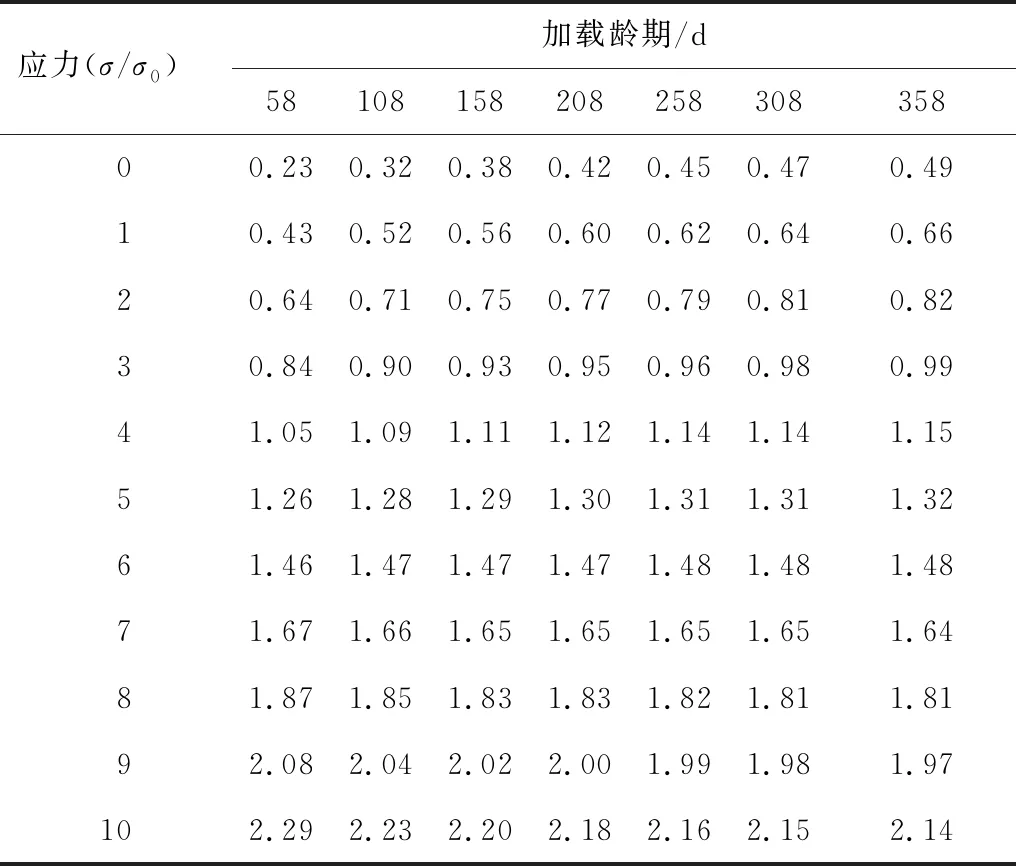
表2 应力水平与预制混凝土加载龄期不同时w1+w2值对照表

4 结论

1)基于平均曲率法分析收缩徐变微差的影响，提出了考虑收缩徐变作用的装配式混凝土叠合梁挠度计算方法。将收缩徐变作用下混凝土叠合梁挠度的理论计算结果和模拟结果进行对比，表明理论计算比数值模拟的结果略大，但在允许范围内且偏安全，且理论计算方法更加简单方便，较适合于工程应用。

2)混凝土叠合梁中徐变微差相对收缩微差较小，收缩徐变微差引起的挠度主要由收缩作用引起，当叠合面处设计应力很小时，为简化计算可以忽略徐变微差的影响。

3)通过敏感性分析发现，不同应力水平下混凝土叠合梁挠度随加载龄期变化呈现不同趋势，应力水平较低时，混凝土叠合梁挠度随预制混凝土加载龄期的增大而增大，反之，挠度随加载龄期的增大而减小。