基于AHP的大学试卷质量评价体系研究
2020-01-11刘云刘熙娟
刘云 刘熙娟

【摘要】教学质量的好坏一致被认为是评价学校综合实力的一个重要因素,判断学校教学质量高低的主要手段就是学生学习能力及学习效果的考核,而试卷又是这一考核的主要媒介。本文根据评价指标筛选原则,从卷面质量、命题质量、考试结果、试卷结构四个方面建立了大学试卷质量评价指标体系。介绍了层次分析法(AHP)的基本原理和方法步骤,并对影响试卷质量的各指标权重进行排序,获得评价指标的总排序。最后对影响试卷质量的因素进行了分析,为提高高校试卷命题的合理化程度做出理论指导。
【关键词】层次分析法 试卷质量 评价指标体系 权重
【基金项目】塔里木大学校长基金(TDZKQN201823)。
【中图分类号】G420 【文献标识码】A 【文章编号】2095-3089(2020)51-0004-02
1.引言
高等学校担负着为国家培养高素质专业技术人员的重要任务,教育教学能力是高校综合实力重要体现,其效果的好坏直接关系着高校自身的生存和发展。目前,大部分高校对专业课、基础课的教学评价方式依然使用传统的“试卷考核法”,考试无疑是衡量学生对课程掌握的程度最好的方式。这种考察方式的优点是组织简单,容易操作,相对公平,在很大程度上能够全面反映学生的学习效果。高质量的试卷对于客观公正、科学合理的评价学生的学习水平尤为重要。通过对试卷质量的分析,探究当前教育教学过程中存在的问题及薄弱环节,努力改进和提高试卷质量,为今后教学效果的考核提供依据,一直是广大教育工作者研究的热点问题之一。目前,已有许多国内学者对试卷质量问题进行了大量卓有成效的研究。比如,邓万友[1]在探究试卷评价相关理论的基础上,详细阐述了试卷评价的指标体系,并利用层次分析法构建了一个网络化的试卷评价系统,实现了试卷评价的现代化与技术化。徐设政[2]应用asp.net技术设计了网络试卷评价系统,并结合自己学校实际,对计算机专业课程试卷进行了合理地评价与分析。李金平[3]以江南大学医学系护理专业预防医学考试卷为例,探讨了试卷的难度、区分度等质量分析指标。俞燕等[4]提出了基于模糊综合评判的高校教师课堂教学质量评价体系的构建及改进。上述学者采用适当的评价方法对他们的体系进行科学的论证,但还有待进一步的完善。基于此,本文以塔里木大学为例将课程考试试卷作为研究对象,选取指标并建立课程考试质量评价指标体系,结合层次分析法给出了体系中各指标的具体权重,并应用层次分析法对课程考试质量进行綜合评价,所得结论对于提高学校教学的评价效率具有切实的意义。
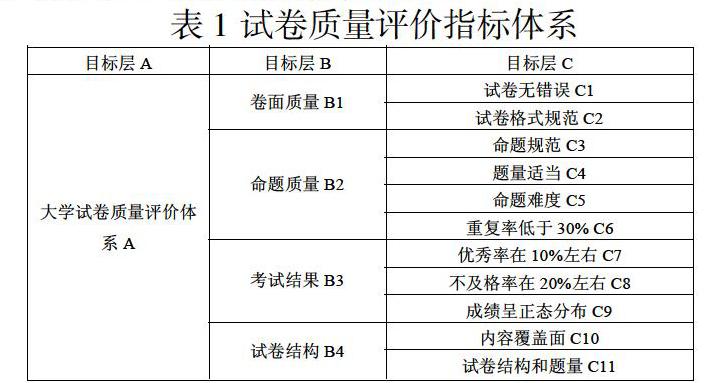
2.试卷质量评价体系
2.1层次分析法
层次分析法(Analytic Hierarchy Process,AHP)是美国运筹学家T.L.Satty提出的一种对复杂现象的决策思维进行系统化、模糊化、数量化的方法[5,6]。运用该方法构造系统模型并计算各指标权重主要分为以下四个步骤:
(1)建立层次结构模型。将决策的目标、考虑的因素(决策准则)和决策对象按他们之间的相互关系分为最高层(目标层)、中间层(准则层)、最低层(指标层),绘出层次结构图。(2)构造判断(成对比较)矩阵。判断矩阵的元素用Santy的1-9标度方法[5,6]给出。(3)层次单排序及其一致性检验。计算各判断矩阵最大特征根λmax及其对应的特征向量,经归一化后得到权重,记为W。根据一致性比率CR=CI/RI,CI=(λmax-n)/(n-1),对判断矩阵进行检验。若CR<0.1, 则说明判断矩阵满足一致性要求;否则,需对判断矩阵的标度做适当修正。(4)层次总排序及其一致性检验。设Wk-1=(W1,W2,…,Wnk-1)表示第k-1层上的nk-1个元素相对于目标层的权重向量,用Pj=(P1j,P2j,…,Pnkj)表示第k层上nk个元素对第k-1层第j个元素为准则的排序权重向量,则第k层元素对目标层的组合权重向量可表示为W=(P1,P2,…,Pnk-1)×Wk-1。
层次总排序的结果也需要进行一致性检验,其一致性比率可按下式计算:
当CR(k)<0.1时,则认为层次总排序通过一致性检验。否则需要重新调整那些一致性比率高的判断矩阵的元素取值。最后,根据最下层(决策层)的层次总排序做出最终决策。
2.2 AHP在试卷质量评价中的应用
2.2.1 指标体系的建立
从卷面质量、命题质量、考试结果、试卷结构分别选取若干能反应这四大效能的指标,见表1。
2.2.2 层次分析法的应用
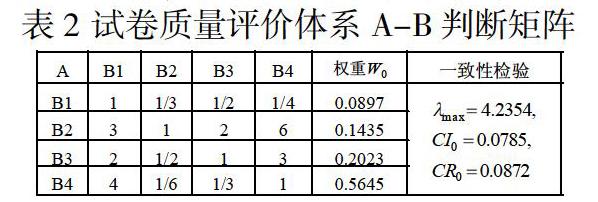
针对以上建立的指标体系,构造试卷质量评价体系A-B判断矩阵,运用层次分析法,通过MATLAB软件实现指标体系各元素的权重计算,并进行一致性检验。结果如下:
同理,可以建立卷面质量B1-C判断矩阵,命题质量B2-C判断矩阵,考试结果B3-C判断矩阵,试卷结构B4-C判断矩阵,结果见表3,4,5,6。
分析上面5个表格可知,CR均小于0.1,满足一致性检验。接下来计算层次总排序,并进行一致性检验,结果见表7。
根据层次分析法原理,可得总体一致性CR=0.0936<0.1,满足一致性检验要求。
CR=CR0+=0.0872+0.0064=0.0936
3.结论
本文利用层次分析法构建了塔里木大学试卷质量评价指标的层次模型,构造了判断矩阵,并采用MATLAB程序进行权重计算,使得各层指标相对权重有效,结果表明:试卷结构和题量,内容覆盖面所占比例比较大。所以,为了提高试卷质量,出卷老师应特别注意试卷结构和题量以及内容覆盖面这两个因素。
参考文献:
[1]邓万友.综合试卷评价体系的构建与实现[J].内蒙古师范大学学报(教育科学版),2006(1):41-44.
[2]徐设政.基于asp.net技术的试卷评价系统的设计与实现[J].工程科技,2008(7):64-65.
[3]李金平.考试质量分析[J].江南大学学报(自然科学版),2004(4):430-434.
[4]俞燕,黄文胜.基于模糊1综合评判的高校教师课堂教学质量评价体系的构建及改进[J].学术平台,2009(1):108-109.
[5]张校玮.基于MATLAB方法南水北调受水县城水资源优化配置方案探讨——以固安为例[J].内蒙古水利,2019(1):47-49.
[6]李靖,周孝德,吴文娟.层次分析法在水环境承载力评价中的应用[J].水利科技与经济,2008(11):866-869.
作者简介:
刘云(1986-),男,讲师,主要从事金融数学和反问题研究。
