受火钢拱结构的冲击响应与弯扭屈曲

王欢 胡亚超 谭英华 席丰

摘要：

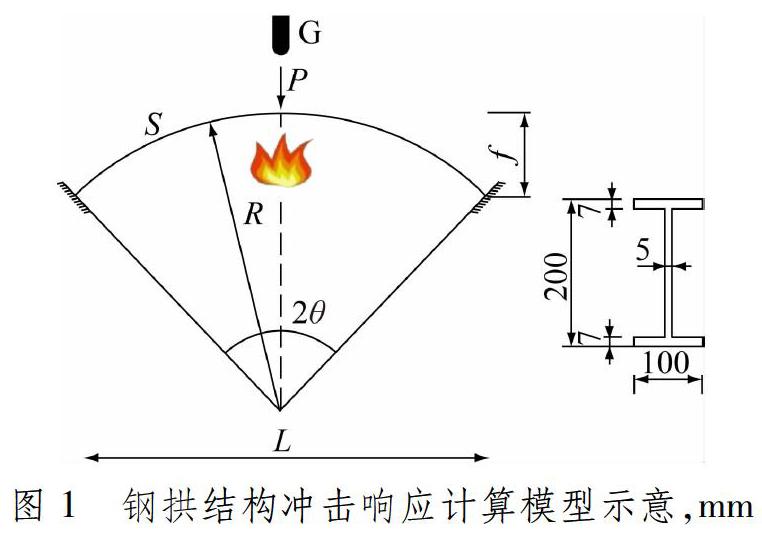
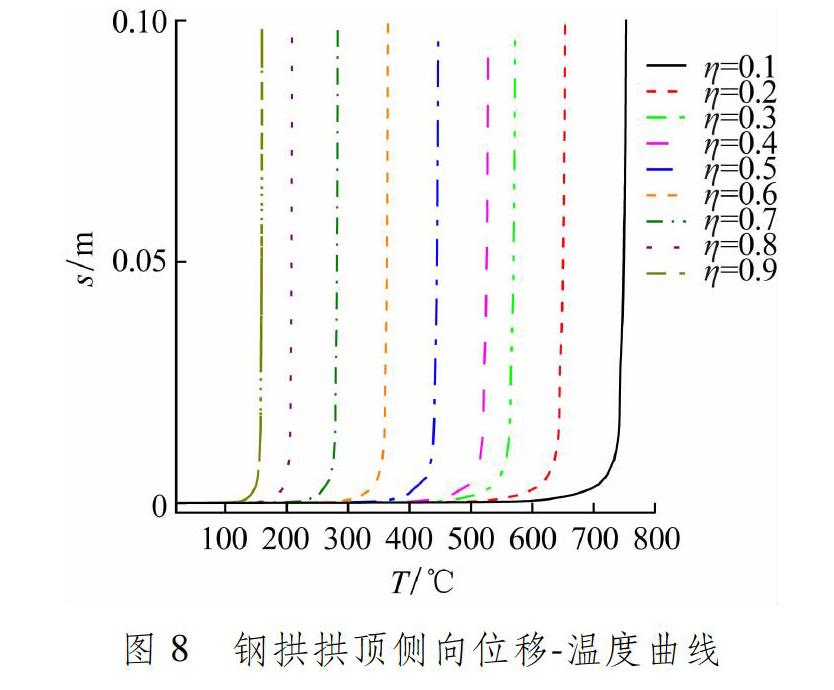
为研究火灾中受质量块撞击两端固支钢拱结构的动力响应和弯扭屈曲行为，利用有限元软件Abaqus对其进行数值仿真，考虑钢材力学性能的升温退化和应变率强化效应，得到临界温度范围内钢拱发生弯扭屈曲时质量块的临界速度，以及撞击荷载作用下钢拱结构的竖向挠度、撞击力变化曲线和响应过程，并对质量块的质量速度关系和拱脚处约束条件进行参数分析。研究结果表明，在不同温度范围内，使钢拱发生弯扭屈曲的质量块临界速度的影响因素不同：20 ℃≤T≤100 ℃时，静载荷比η起主要作用;100 ℃

关键词：

温度; 撞击; 钢拱; 动力响应; 弯扭屈曲

中图分类号：  TU328; TP391.92

文献标志码：  B

Impact response and flexural torsional buckling of steel arch structure in fire

WANG Huan， HU Yachao， TAN Yinghua， XI Feng

（Civil Engineering School， Shandong Jianzhu University， Jinan 250101， China）

Abstract：

To study the dynamic response and flexuraltorsional buckling behavior of the steel arch structure in fire with fixed supports at both ends under the impact of mass block， the numerical simulation is carried out using finite element software Abaqus. The effect of temperature degradation and strain rate strengthening on mechanical properties of steel is considered， and then the critical velocity of the mass block is obtained while the steel arch is subjected to bending and torsion buckling within the critical temperature range， and the vertical deflection， impact force curve and response process of steel arch structure under impact load are computed. The massvelocity relationship of the mass block and the constraint conditions at the arch foot are analyzed. The results show that， while the steel arch is subjected to flexuraltorsional buckling in different temperature ranges， the influence factors on the critical velocity of mass block are as follows： while 20 ℃≤T≤100 ℃， the static load ratio η plays the major role; while 100 ℃

Key words：

temperature; impact; steel arch; dynamic response; flexuraltorsional buckling

0 引 言

近年來，火灾和爆炸事故频繁发生，并且这些事故均为火灾伴随着重物冲击或爆炸等偶然载荷的共同作用。火灾高温导致建筑结构承载力下降，爆炸载荷瞬时作用又释放巨大能量，导致建筑物严重破坏甚至倒塌，危害公众的生命和财产安全。对火灾和撞击载荷耦合作用下的结构进行研究，具有重大现实意义。

拱形结构可将其上部承受的竖向载荷转化为拱脚处的水平推力，利用自身弧形轴线将载荷作用产生的弯矩转化为轴向压力，具有较高的承载能力且造型优美，因此被广泛应用于工业厂房、山区防护棚和隧道等大型公共建筑中。

现有火灾中拱形结构的研究主要基于平面内理论推导或者数值模拟分析，如：PI等[12]研究均匀温度场下两端固支圆拱和两端铰支浅圆拱平面内的非线性热屈曲行为，得到其屈曲载荷的解析解;HEIDARPOUR等[34]分析得到均布载荷和火灾共同作用下两端弹性约束拱结构的非线性热弹性行为公式，并探究高温下拱结构的受力性能;MOGHADDASIE等[5]研究热环境下浅圆拱受静载作用时的位移场、承载能力和临界点位置;GUO等[6]研究发现，高温下两端铰支圆弧拱水平约束刚度和截面几何尺寸对结构承载力的影响比载荷比的影响更大;LU等[7]研究均匀热环境下考虑剪切变形的任意径向载荷作用圆拱的侧向扭转屈曲行为。

冲击载荷包括阶跃冲击载荷、跌落撞击载荷、瞬时脉冲载荷和爆炸载荷等。关于冲击载荷作用下拱形结构动力屈曲行为的研究有很多。LIU等[89]分析得到集中周期載荷作用下拱结构平面外动力失稳的2个屈曲条件。康婷等[1011]基于BR准则系统研究拱结构的弹塑性动力响应及其屈曲行为。

上述研究主要针对高温和冲击载荷单独作用下的拱结构行为，并且大部分是关于拱平面内的行为分析。对火灾和冲击载荷联合作用下结构行为的研究主要集中于梁和柱等构件[1215]，鲜有关于火灾和冲击载荷共同作用下拱结构行为的研究[16]。本文主要研究高温和撞击载荷共同作用下钢拱结构的动力屈曲行为，考察不同静载荷比条件下圆拱在临界温度内发生弯扭屈曲时质量块的临界速度，以及在撞击作用下钢拱拱顶的竖向挠度、响应过程和撞击力时程曲线，分析撞击物质量、质量块速度和拱脚约束条件对结构承载力的影响。

1 问题描述和钢拱结构有限元模型

1.1 问题描述

研究对象为两端固支钢圆拱，常温环境温度为T0=20 ℃。火灾环境温度达到预定值时，质量块G从高处下落撞击拱顶，研究分析钢拱的动力响应。钢拱结构冲击响应计算模型示意见图1。拱结构跨度L=3 m，半径R=2.175 m，矢高f=R（1-cos θ），矢跨比f/L=0.2。圆拱采用工字钢加工而成，其截

面高度为200 mm、宽度为100 mm、翼缘厚度为7 mm、腹板厚度为5 mm。质量块G的质量m=120 kg，宽度为30 mm、高度为60 mm、长度为100 mm。

定义静载荷比η=P/Pcr，P为拱顶处施加的集中静载荷，Pcr为常温下圆拱的临界载荷。

考虑结构四面受火，火灾下周围环境的升温时间过程采用ISO834标准升温曲线（见图2），因此t时刻的温度T=T0+345 lg（8t+10）。

1.2 钢拱结构有限元模型

由于钢拱跨中在短时间内受到质量块的冲击，为防止结构局部屈曲严重和剧烈反应引起误差，对钢拱跨中两侧设置加劲肋，其厚度与工字钢翼缘厚度相同，对距跨中0.2 m区域的网格进行局部加密。为避免应力

集中，将集中静载荷P等效成竖向均布载荷施加于拱顶，均布载荷作用区域的弧长与钢拱横截面宽度相等。钢拱结构两端面分别耦合于2个参考点，并对参考点施加约束，模拟两端固支。钢拱结构有限元模型见图3。

1.2.1 钢材料本构模型

钢拱材料选用Q235B钢，常温下材料的弹性模量E=206 GPa，屈服应力σ0，s=290 MPa，密度ρ=

7 850 kg/m3，泊松比为0.3。

钢拱材料采用理想弹塑性模型，其应力应变关系见图4，其中：E和ET分别为常温T0和温度T时的弹性模量;σ0，s和σ0分别为常温T0时的静态屈服应力和动态屈服应力;σT，s和σT分别为温度T时的准静态屈服应力和动态屈服应力。

低碳钢的弹性模量和屈服应力随温度升高而降低，本文采用标准EN 199318[17]规定的材料性能折减因数，见图5。弹性模量折减因数κE，T=ET/E，屈服应力折减因数κs，T=σT，s/σ0，s。

钢材为应变率敏感材料，受撞击载荷作用时其屈服应力增大，本文采用考虑应变率效应的CowperSymonds本构模型，其动态屈服应力为

式中：ε·为钢材等效塑性应变率;D（T）和q（T）为温度T时钢材的应变率参数。SYMONDS等[18]提出：在常温下钢材的应变率参数为D=40 s-1，q=5;温度T=1 000 ℃时钢材的应变率参数为D=400 s-1，q=1。将常温和1 000 ℃时钢材的应变率参数进行插值，即可得到与温度相关的2个应变率参数D（T）和q（T）。[12]

1.2.2 钢材热工参数

对钢拱结构进行温度场分析时，均采用文献[17]规定的相关热工材料参数，具体如下。

热膨胀系数

钢材的密度和泊松比受温度影响较小，高温下钢材的密度和泊松比可按常温取值。

1.2.3 常温下钢拱结构的临界载荷

《钢结构工程施工质量验收规范》[19]规定，梁和轴心受压柱安装侧向弯曲允许偏差为L/1 000（L为构件轴线长度）。本文统一引入S/1 000（S为弧长）作为钢拱结构的几何初始缺陷，对结构进行弯扭屈曲模态分析。对钢拱拱顶施加静载荷，得到两端固支钢拱拱顶的侧向位移载荷曲线，见图6。当拱顶静载荷增加至33.57 kN时，钢拱发生弯扭屈曲，说明常温下钢拱的临界载荷Pcr=33.57 kN。

2 计算步骤和单元收敛性检验

2.1 计算步骤

火灾环境中受静载荷作用的钢拱受到质量块撞击时，由于撞击过程非常短暂，可假定温度保持不变。依据加载顺序，模拟过程分为3个步骤。

（1）首先，进行钢拱结构的屈曲模态分析，并引入几何初始缺陷;然后，对钢拱拱顶施加静载荷，进行静力学分析。

（2）保持静载荷的作用，按照图2的升温曲线对结构进行升温，分析钢拱结构的应力变化和变形行为。

（3）利用重启动分析，将第（2）步中受火灾中的钢拱结构模型作为初始状态导入本阶段进行显式动力学分析。考虑高温下钢材的应变率效应，通过对质量块施加初始速度实现对钢拱撞击载荷的施加，分析撞击载荷作用下钢拱结构的动力响应。

2.2 单元收敛性检验

在数值模拟中，钢拱采用壳单元S4R模拟。在撞击分析时，质量块采用离散刚体单元R3D4模拟，将其置于拱顶的正上方10 mm处，施加初始速度vG，质量块与钢拱之间的摩擦因数取0.2。当静载荷比η=0.3、质量块初始速度vG=15 m/s、温度T=400 ℃时，采用不同网格尺寸计算得到的拱顶竖向挠度峰值和撞击力峰值对比见表1，拱顶竖向挠度和撞击力变化曲线见图7。由此可知，当网格较密时，拱顶竖向挠度和撞击力十分接近，误差在2%以内，故钢拱网格数目为11 000时进行数值模拟分析即可得到較为精确的结果。

3 高温下受撞击钢拱结构的动力响应

3.1高温下使钢拱发生弯扭屈曲的质量块临界速度

静载荷比η取0.1～0.9时，对应的临界温度Tcr见图8。在升温过程中，由于热膨胀效应和高温软化作用，拱结构产生热弯曲，导致其偏离原来的平衡位置，发生平面外失稳。根据拱顶侧向位移变化曲线可确定其临界温度，将曲线开始出现拐点时的温度定为临界温度。在临界温度范围内，使钢拱发生平面外弯扭屈曲的质量块临界速度vcr见图9。

由此可知，随着η增大或T升高，vcr呈非线性递减趋势。结合钢材弹性模量和屈服应力折减因数可知，当20 ℃≤T≤100 ℃时，随温度升高，钢材的强度和刚度保持不变，影响vcr的主要因素是η，且当

η>0.6时，vcr减小趋势加剧。当100 ℃

3.2 高温下受撞击钢拱的竖向挠度峰值和撞击力峰值变化规律

η=0.3、质量块速度vG为12～25 m/s时临界温度范围内拱顶竖向挠度峰值wmax和撞击力峰值Fmax的变化规律见图10和11。

由图10可知，随着T升高或vG增大，钢拱结构抵抗撞击的性能下降，竖向挠度峰值不断增大。在相同温度下，当vG>22 m/s时，质量块下落过程中产生巨大的撞击能量，结构进入塑性大变形阶段，挠度峰值急剧增大。在相同速度下，当T>300 ℃时，在温度和静载荷比的作用下，钢材结构挠度峰值急剧增大。

由图11可知，随着T升高或vG增大，拱顶撞击力峰值减小。在T<300 ℃情况下，vG<20 m/s时拱顶受到的撞击力峰值急剧减小，而vG≥20 m/s时拱顶受到的撞击力峰值减小缓慢。结合图10可知，当T<300 ℃时，结构仅刚度下降，因为大速度作用产生的动能更大，所以结构挠度峰值急剧增大;依据能量准则，大速度作用产生的撞击力峰值小于小速度作用下产生的撞击力峰值。在相同速度下，当T≥300 ℃时，结构承载能力下降和钢材高温软化现象使得撞击力峰值急剧下降。

根据图10和图11中挠度峰值和撞击力峰值随温度的变化规律可知，vG=22 m/s是拱顶挠度峰值和撞击力峰值出现明显变化的临界点。在此撞击速度下，高温时受撞击钢拱拱顶的侧向位移曲线见图12。随着温度升高，热膨胀效应和材料软化作用加剧，结构发生较大的平面外偏转，更易加剧拱结构平面外弯扭屈曲。

3.3 高温撞击过程中钢拱的动力响应变化规律

定义无量纲撞击力F/Fmax、无量纲挠度w/wmax和无量纲速度vG/vG，max（vG，max为质量块最大初始速度）。当静载荷比η=0.3，对T分别为20和400 ℃时受质量块撞击钢拱的动力响应行为进行研究，得到撞击过程中无量纲撞击力、无量纲挠度和无量纲速度曲线，见图13。由此可见，不同温度对应的无量纲物理量变化规律一致。

在整个撞击过程中，3个无量纲物理量撞击响应曲线均可分为4个阶段：OA为突增阶段，AB为反弹阶段，BC为下降阶段，CD为卸载阶段。在OA阶段，短时间内质量块下落撞击钢拱拱顶，质量块与拱顶接触瞬间撞击力达到峰值，同时质量块速度快速下降。OA段钢拱结构受质量块撞击后发生一定变形导致撞击力下降，之后质量块持续作用在结构上，撞击力出现第二个峰值点B。在AB阶段，质量块速度下降的同时撞击力迅速降低，随后拱顶撞击力达到另一个的峰值点B。在BC阶段，B点之后拱顶撞击力持续下降，并伴随着小幅度的震荡。质量块速度呈非线性的持续下降趋势，结构挠度快速增大，质量块速度减小为0时挠度达到峰值。在CD阶段，C点之后质量块与结构开始分离并发生反方向回弹，速度反方向增大;随着质量块向上回弹，拱顶竖向挠度呈现减小趋势。D点质量块速度达到反方向的峰值，撞击力减小为0。随着时间的持续，拱顶挠度在平衡位置震荡，质量块保持反方向的速度峰值不变。

4 参数分析

4.1 质量块的质量速度组合工况的影响

当静载荷比η=0.3、温度T=200 ℃时，保持动能E=11 760 J不变，探究质量块在不同质量速度组合情况下（见表2）受质量块撞击钢拱的动力响应行为。

在质量块不同质量速度组合工况下钢拱拱顶竖向挠度曲线见图14。当动能一定时，质量块质量越大，挠度峰值越大。由此可知，大质量、低速撞击更易导致钢拱结构变形破坏。在B1工况下，拱顶因竖向挠度过大而失效。对比不同工况可知，拱顶最终竖向挠度随着质量块的质量增大而增大。

在不同质量速度组合工况下钢拱拱顶撞击力曲线见图15。动能一定时，撞击力峰值随撞击质量增加而减小，质量块与拱顶接触时间增加。

不同质量速度组合工况下拱顶的最大侧向位移曲线见图

16。随着质量块质量的减小（速度增大），拱顶的最

大侧向位移逐渐减小，当m=235.20 kg（速度为10 m/s）时，拱顶最大侧向位移曲线出现拐点，即B3工况是钢拱发生平面外弯扭屈曲的临界工况。在不同

质量速度组合工况下钢拱结构的弯扭屈曲变形见图17。随着质量块质量的减小（速度增大），钢拱结构的平面外弯扭屈曲程度逐渐减小。

4.2 边界条件的影响

拱脚约束包括平面内约束和平面外约束。在一般情况下，约束拱脚3个方向的平动位移，改变3个方向的转动约束，组成不同类型的拱脚约束方式。本文考虑3种支座约束类型，见表3，其中Tcr为η=0.3时的取值。

为与第3.2节对比，选择η=0.3，vG为12～25 m/s时临界温度范围内3种支座钢拱的拱顶竖向挠度峰值wmax和撞击力峰值Fmax对比分别见图18和19。

由图18可知，在相同工况下，拱顶竖向挠度变化趋势一致，面内铰接即IPOF支座钢拱结构的抗撞击能力较强。IPOF支座的钢拱结构将高温下产生的附加轴力和弯矩释放，因此拱脚处受力减小，说明释放面内转动约束可有效提高结构抵抗钢拱结构高温下的抗撞击能力。

由图19可知，在相同工况下，FF和IPOF支座形式钢拱结构的撞击力变化趋势一致，但IFOP支座形式钢拱结构的撞击力峰值远小于前二者，且在大速度下出现明显不同。在FF、IPOF支座形式下：当vG≤16 m/s时，撞击力峰值突减;当vG>16 m/s时，随着vG增大撞击力峰值下降速度缓慢。在IFOP支座形式下，vG≥22 m/s时的撞击力峰值突减，其他范围内的撞击力峰值变化幅度较小。分析原因可知，在静载荷升温阶段，IFOP支座形式下的钢拱结构产生较大的面外位移，因此在撞击载荷作用下其承载力远小于其他支座形式下的钢拱，说明面外约束可降低钢拱结构的抗撞击承载力。

5 结 论

通过有限元数值分析，研究火灾中受质量块撞击钢拱结构的动力响应与屈曲行为，得到高温下两端固支钢拱发生弯扭屈曲的临界速度，探讨高温撞击过程中钢拱结构和质量块的撞击响应规律。通过参数分析研究质量块的質量速度和钢拱的边界条件对高温下受质量块撞击钢拱动力响应的影响，得出以下主要结论。

（1）钢拱结构的临界温度随着静载荷比的增加而减小，其发生平面外弯扭屈曲对应的质量块临界速度也减小。根据高温下弹性模量和屈服应力折减因数，得到不同温度范围内使钢拱发生平面外弯扭屈曲的质量块临界速度的主要影响因素：当20 ℃≤T≤100 ℃时，静载荷比η起主要作用;当100 ℃

（2）在高温撞击过程中，随着火灾温度升高和质量块速度的增大，拱顶竖向挠度峰值增大，撞击力峰值减小，质量块作用持续的时间增加。

（3）分析高温撞击过程中钢拱结构和质量块的撞击响应规律，可将撞击响应曲线分为4个阶段，即突增阶段、反弹阶段、下降阶段和卸载阶段。

（4）当保持动能不变时，在大质量、低速质量块的撞击作用下，钢拱结构的整体动力响应更为剧烈，更易引发钢拱结构的平面外弯扭屈曲。

（5）在高温撞击过程中，与拱脚的平面内约束相比，其平面外约束对钢拱结构的动力响应更为不利。因此，释放平面内转动约束有利于提升高温撞击载荷作用下钢拱结构的抗变形能力。

参考文献：

[1]PI Y L， BRADFORD M A. Inplane thermoelastic behaviour and buckling of pinended and fixed circular arches[J]. Engineering Structures， 2010， 32（1）： 250260. DOI： 10.1016/j.engstruct.2009.09.012.

[2] PI Y L， BRADFORD M A. Effects of nonlinearity and temperature field on inplane behaviour and buckling of crownpinned steel arches[J]. Engineering Structures， 2014， 74： 112. DOI： 10.1016/j.engstruct.2014.05.006.

[3] HEIDARPOUR A， ABDULLAH A A， BRADFORD M A. Nonlinear thermoelastic analysis of steel arch members subjected to fire[J]. Fire Safety Journal， 2010， 45（3）： 183192. DOI： 10.1016/j.firesaf.2010.02.004.

[4] HEIDARPOUR A， ABDULLAH A A， BRADFORD M A. Nonlinear inelastic analysis of steel arches at elevated temperatures[J]. Journal of Constructional Steel Research， 2010， 66（4）： 512519. DOI： 10.1016/j.jcsr.2009.10.003.

[5] MOGHADDASIE B， STANCIULESCU I. Equilibria and stability boundaries of shallow arches under static loading in a thermal environment[J]. International Journal of NonLinear Mechanics， 2013， 51： 132144. DOI： 10.1016/j.ijnonlinmec.2013.01.001.

[6] GUO Z， WANG Y C， LU N， et al. Behaviour of a twopinned steel arch at elevated temperatures[J]. ThinWalled Structures， 2016， 107： 248256. DOI： 10.1016/j.tws.2016.06.015.

[7] LU H W， LIU A R， PI Y L， et al. Lateraltorsional buckling of arches under an arbitrary radial point load in a thermal environment incorporating shear deformations[J]. Engineering Structures， 2019， 179： 189203. DOI： 10.1016/j.engstruct.2018.10.071.

[8] LIU A R， LU H W， FU J Y， et al. Analytical and experimental studies on outofplane dynamic instability of shallow circular arch based on parametric resonance[J]. Nonlinear Dynamics， 2017， 87： 677694. DOI： 10.1007/s1107101630687.

[9] LIU A R， YANG Z C， BRADFORD M A， et al. Nonlinear dynamic buckling of fixed shallow arches under an arbitrary step radial point load[J]. Journal of Engineering Mechanics， 2018， 144（4）： 04018012. DOI： 10.1061/（ASCE）EM.19437889.0001425.

[10] 康婷， 許金余， 白应生， 等. 爆炸冲击荷载作用下拱结构的弹塑性动力响应研究[J]. 兵工学报， 2013， 34（9）： 10971102. DOI： 10.3969/j.issn.10001093.2013.09.007.

[11] 康婷， 许金余， 白应生， 等. 爆炸冲击荷载作用下拱结构动力屈曲研究[J]. 空军工程大学学报（自然科学版）， 2015， 16（6）： 7983. DOI： 10.3969/j.issn.10093516.2015.06.017.

[12] XI F. Large deflection response of restrained steel beams under fire and explosion loads[J]. Springer Plus， 2016， 5（1）： 27386235. DOI： 10.1186/s4006401625096.

[13] TAN Y H， XI F， LI S C， et al. Pulse shape effects on dynamic response of a steel beam under combined action of fire and explosion loads[J]. Journal of Constructional Steel Research， 2017， 139： 484492. DOI： 10.1016/j.jcsr.2017.10.001.

[14] 张莹， 侯博晗， 席丰. 不同温度下约束钢梁的落锤冲击响应分析[J]. 防灾减灾工程学报， 2018， 38（6）： 10261032. DOI： 10.13409/j.cnki.jdpme.2018.06.018.