不同化探数据处理方法的对比研究
2020-01-10
(四川省地质矿产勘查开发局二零七地质队,四川 乐山614000)
本文以江西大浩山金矿1∶1万土壤化探数据中的Ag、Au、Cu、As元素为例,采用传统统计方法、趋势面法和含量-面积法计算的异常下限或筛选的异常进行对比分析,以确定适用于该区的化探数据处理方法,然后进行异常圈定,以指导大浩山金矿兆吉沟矿段外围的找矿工作。
1 研究区地质概况
研究区位于皖赣交界之江西省彭泽县境内。中元古代以来,区域上形成了以变凝灰质砂岩、变杂砂岩、板岩、千枚岩为主,夹流纹岩、细碧角斑岩等海相火山岩的浅变质岩系——双桥山群,为该区域的基底地层。澄江期在晋宁褶皱造山带的山前和山间坳陷中堆积了以杂砂岩为主的磨拉石夹火山碎屑岩建造,造就了震旦系下统莲沱组金多金属矿源层。印支运动,使大陆裂谷褶皱封闭,并形成了一系列区域北东向断裂构造,伴随有岩浆活动,在断裂构造体系中的热水环流和岩浆热液的双重作用下,矿源层中的金多金属被萃取活化迁移,在次级近东西向断裂构造中富集成矿[1]。区内岩浆岩分布较少,多以花岗斑岩脉、石英斑岩脉、闪长玢岩脉和煌斑岩脉产出(图1)。

图1 研究区地质简图
2 化探数据处理方法
2.1 传统统计法
运用传统统计法的一个重要前提是元素含量数据服从正态或者对数正态分布。但是百分百服从正态分布或对数正态分布的数据基本上没有。如果数据不符合正态或者对数正态分布,就必须对化探数据进行处理,处理方法一般是采用以平均值(X)+3*标准偏差(S)为上阙值,以平均值(X)-3*标准偏差(S)为下阙值,进行迭代剔除,直到没有超出上下阙值的数据为止,这样所有数据分布在X-3S 与X+3S之间,在这个范围内的数据之平均值为背景值,异常下限等于背景值加2倍标准偏差[2]。
2.2 趋势面法
趋势面法将地球化学数据分为区域性变化、局部性变化和随机性变化三部分,区域性变化是由区域地质背景造成的总体规律性变化,局部性变化是小范围的变异造成的,随机性变化是随机因素造成的[3]。这样化探值就被分解为3 部分:Zi=Ti+Ni+Ei,其中:Zi为观测值,Ti反映区域性变化,Ni反映局部的变化,Ei为随机性变化部分。首先要将局部性变化Ni从观测值中分离出来,然后从局部性变化Ni 中分出随机性变化Ei,最后就得到有地质内涵的异常值。
具体做法:①数据预处理:实际工作中多用低值总体累计频率95%处的分位值作为高样品值的临界值,凡是高于临界值的观测值都用临界值代替[4];②趋势提取过程:对预处理后的数据用Sufer软件进行趋势面计算,得到残差值。③计算异常值:异常值=残差值-正残差值的平均值。
2.3 含量-面积法
目前,应用分形理论确定异常下限的方法主要有含量-频数法[5]、含量-面积法[6]、含量-周长法[7]以及含量-总量法[8]等,本文采用含量-面积法。
所谓分形是整个事物的一个组成部分在形状上与整体有一定的相似性,它具有自相似性[9]。自相似性是在形态、功能、结构以及信息等方面有统计意义上的相似性[10]。分维数是一个描述这种自相似性的参数。分形分布的特点要求大于等于某一尺度的数目或和数,与物体大小之间存在幂函数关系,即N(r)=Cr-Dr>0。
式中,r表示特征尺度;C>0 称为比例常数;D>0 称为分维数;N(r)=N(≥r)表示尺度大于等于r的数目或和数[11]。
为了求出分维数D,将观测数据〔(N(r1),N(r2),…,N(rn))和(r1,r2,…rn) 〕转换为以10为底的对数后,绘制双对数散点图,如果其散点的分布可以大致拟合成一条直线,其分维数D 就等于拟合直线的斜率的绝对值[11]。若拟合成三段直线,则求出第二段与第三段直线的分界点对应的含量值为异常下限。
具体做法是:将不同元素含量值r及其所围成的平面面积N(r)转换对数,绘制成Lgr-LgN(r)双对数散点图,最后用Grapher 拟合直线,求得分维数和分界点含量值,以第二个分界点对应的含量值为异常下限(表)。4种元素Lgr-LgN(r)关系图见图2。
从以上4种元素Lgr-LgN(r)关系图可以看出,各元素Lgr-LgN(r)关系图都拟合出三段直线,表明研究区4种元素地球化学场具有多重分形的结构特征[12]。

传统统计法与含量-面积法异常下限对比表
3 不同方法的效果对比
3.1 不同方法确定的异常下限对比
由于趋势面法只能得到异常值,无法确定异常下限,所以只能将传统统计法与含量-面积法进行对比。从表1中可以看出,四种元素含量-面积法确定的异常下限均比传统统计法小。其原因是传统统计法迭代剔除离群值后得到的背景数据仍呈偏态分布,从而导致计算的背景值偏高。含量-面积法利用全部数据分析发现其为多重分形分布的事实,从而获取了与之不同的异常下限。

图2 Ag、Au、Cu、As 四种元素Lgr-LgN(r)关系图
3.2 不同方法圈定的异常对比和认识
从图3中可以看出,三种方法圈出的Ag元素异常形态和分布基本一致,沿北东向断裂及其次级断裂展布,主要分布于震旦系灯影组、陡山沱组和莲沱组地层中。传统统计法与含量-面积法比较:含量-面积法求出的异常下限更低,异常面积更大,圈出了传统统计法未表现出来的低异常,圈出的异常沿北东向断裂展布的性质更明显,连续性更好,浓集中心更明显。趋势面法圈出的异常与传统统计法圈出的异常极其相似。根据详查资料,大浩山金矿兆吉沟矿段金矿体伴生银,而只有含量-面积法圈出的异常在兆吉沟矿段内有微弱异常显示。

图3 Ag元素不同方法异常对比图
从图4中可以看出,三种方法圈出的Au元素异常形态和分布基本一致,大多分布于莲沱组地层中沿北东向断裂及其次级断裂展布。传统统计法与含量-面积法比较:含量-面积法计算的异常下限更低异常面积更大,浓集中心更明显,圈出了传统统计法未表现出来的低异常,避免漏掉与矿化有关的弱异常。趋势面法圈出的异常与传统统计法圈出的异常较为相似。根据详查资料,大浩山金矿兆吉沟矿段金矿体呈近东西向产出,三种方法圈定的异常整体均呈近东西向展布,但含量-面积法圈定的异常浓集中心更明显,异常强度最高,连续性最好,与金矿体套合程度最高此外,含量-面积法圈定的异常受断裂控制的迹象更明显。
从图5中可以看出,含量-面积法和趋势面法圈出的Cu元素异常形态和分布基本一致。传统统计法与含量-面积法比较:含量-面积法求出的异常下限比传统统计法求出的异常下限低,异常面积更大,浓集中心更明显,圈出了传统统计法未表现出来的低异常。

图4 Au元素不同方法异常对比图
从图6中可以看出,传统统计法和趋势面法圈出的As元素异常形态和分布基本一致,只是传统统计法圈出的异常面积稍大于趋势面法圈出的异常面积。传统统计法与含量-面积法比较:含量-面积法求出的异常下限更低,异常面积更大,圈出了传统统计法未表现出来的低异常。
综上所述,同一元素采用不同方法确定的异常下限或获取的异常存在明显的差异,含量-面积法计算的异常下限均比传统统计法低很多,趋势面法虽不能计算异常下限,但从圈定的异常面积来看,趋势面法圈出的异常值均比含量-面积法高。趋势面法圈出的Cu元素异常与含量—面积法较为相似,只是趋势面法圈出的Cu元素异常面积比含量—面积法的略小,比传统统计法的异常面积大,说明趋势面法也是考虑了地球化学数据的空间分布特征;其余三种元素的异常是趋势面法与传统统计法相似,其原因之一是这三种元素经两种方法处理后得到的背景数据的分布特征相似,原因之二是趋势面法与传统统计法在原理上都有地球化学场为光滑的连续曲面这一相似点。另外,趋势面法和传统统计法圈出的异常面积均比含量—面积法小,故它二者圈出的异常值相对于含量—面积法偏高。
趋势面法与传统统计法在原理上具有相似点,在经过趋势面拟合和迭代剔除这两种方法处理后得到的背景数据的分布特征相似的情况下,趋势面法圈出的异常与传统统计法相似,相反,趋势面法圈出的异常会与含量-面积法相似,这时得到的异常值就比传统统计法低得多。无论哪种情况,趋势面法得到的异常值都存在偏高现象,同样会丢失跟隐伏矿体有关的弱异常信息。但与传统统计法比较具有一定的优越性,趋势面法的背景值是变化的,在区域上不采用同一标准,从这点来看,趋势面法比较适合于大面积化探数据处理。
含量-面积法根据本区元素含量数据的多重分形分布特征,可以有效的区分负异常区域、背景区域和正异常区域。含量-面积法与传统统计法、趋势面法相比,显著地降低了异常下限,在保障高值异常信息的情况下,不丢失可能与矿化有关的弱异常信息,但会给异常查证带来困难。综合地球化学场空间分布特征与地质构造分析可以得出,采用含量-面积法确定的异常下限更适合本区,其圈定的异常对大浩山金矿兆吉沟矿段外围的找矿工作更具指导意义。另外,通过不同化探数据处理方法的对比,笔者认为异常下限与元素含量数据的空间分布特征和处理方法原理有关。因此,甄别研究区各元素含量数据的空间分布特征以及进行不同化探数据处理方法之间的对比对找矿工作至关重要。
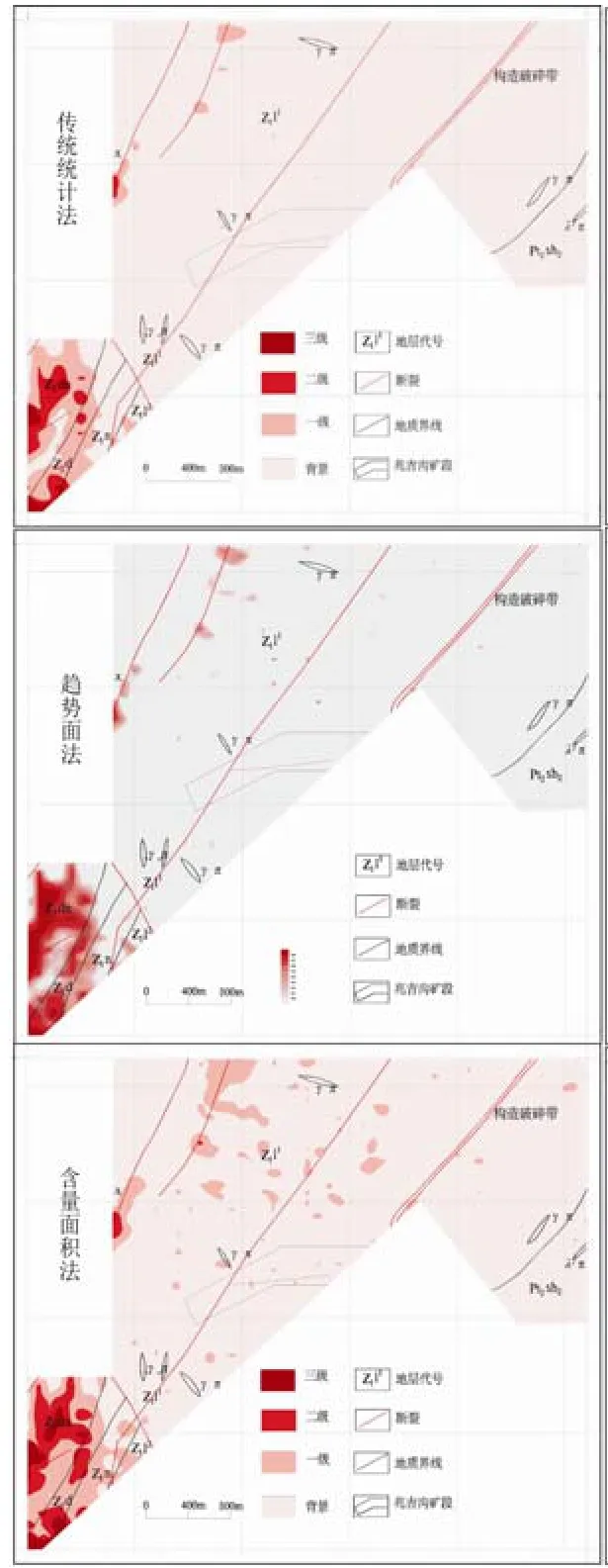
图5 Cu元素不同方法异常对比图

图6 As元素不同方法异常对比图
4 结论
通过前述分析,可以得出如下结论:
同一元素采用不同方法确定的异常下限或获取的异常存在明显的差异,含量-面积法计算的异常下限均比传统统计法低很多,趋势面法虽不能计算异常下限,但从圈定的异常面积来看,趋势面法圈出的异常值均比含量-面积法高。
由于研究区地球化学场数据并不符合正态分布,即使经过取常用对数处理,仍不符合正态分布,其所确定的异常下限仍然会偏高,所以传统统计法会丢失跟矿化有关的弱异常信息。
研究区地球化学元素含量数据具有明显的多重分形分布特征,通过与研究区地质特征对比,认为含量-面积法确定的异常下限更适合本区。因此,甄别各元素含量数据的空间分布特征以及进行不同化探数据处理方法之间的对比,对找矿工作至关重要。
