对H-H连通率估计模型的讨论

2020-01-10

四川地质学报 2019年4期

（成都理工大学地质灾害防治与地质环境保护国家重点实验室，成都 610095）

连通率是影响岩体稳定性的一重要指标，并对岩体稳定性起着控制性的作用。由于结构面在空间发育的不稳定性、不均匀性和野外露头的局限性[1]，因此，准确计算出与实际工程相符的连通率仍是一个难题。

H-H连通率估计模型（窗口法）是基于迹长均值的估计方法，并在实际中得到了较为广泛的应用。然而，该方法具有较为明显的尺度效应[2]，部分情况下的计算结果与实际情况不符。为此，大量改进修正方法被提出。如：范留明[3,4]提出了一种广义H-H迹长估算方法，该方法能较好的消除Laslett对长迹长估计的局限性；杨春和[5]提出采用同心圆法和相切圆法，并对岌岌采石场岩体节理的平均迹长和迹线中点的密度进行估计，分析表明采用相切圆法能够得出稳定、具有一致性的结果；王贵宾[6]得出当圆形窗口的直径与测线法删节长度相等时，扩展测线法和圆形窗口法估计所得的岩体节理平均迹长比较接近；吴琼[7]等在考虑结构面迹长和迹线与统计窗边线的交角均遵循一般概率分布类型的基础上,从概率统计角度推导出窗口法中结构面平均迹长的估算公式。根据取样窗口尺寸相对于不连续面的尺寸关系，划分修正连通率计算适用条件三种情况。目前这方面报导较少；本文通过连通率计算式的修正研究；以期能为连通率计算提供一种合理的修正模型。

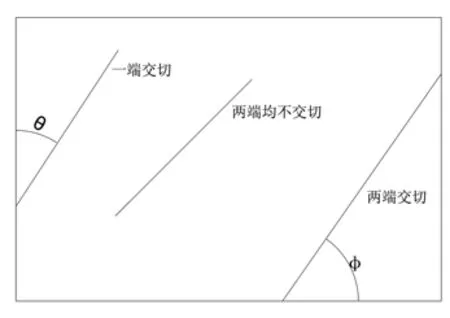
图1 迹线与窗口交切关系

1 H-H连通率估计模型

1.1 H-H迹长均值估计模型

H-H连通率估计模型是以H-H迹长均值估计模型为基础，通过从不连续面与窗口交切的充要条件出发，在测量区取一个矩形窗口，设窗口长为w，高为h，与窗口交切的迹线有3种情况，两端可见、一端可见和两端均不可见[8](图1)。只需统计与窗口存在不同交切关系的裂隙数量，根据交切几何概率求出平均迹长；同上述思路再推导不连续面平均间断长的估算公式，进而根据连通率的定义求出连通率。该模型避免了复杂的计算过程，在实际工程中有着广泛的应用[9]。

根据实测数据，假设两端可见的迹线有n2条，一端可见的迹线n1条，两端均不可见的迹线n0条，总的迹线数量为N条[10]。若迹线中点在窗口内部服从均匀分布，则迹线与窗口顶边或底边交切的充要条件为[11]：

同理，迹线与窗口左边或右边交切的充要条件为：

与窗口顶边或底边交切记作事件A，则概率P(A)可表示为：

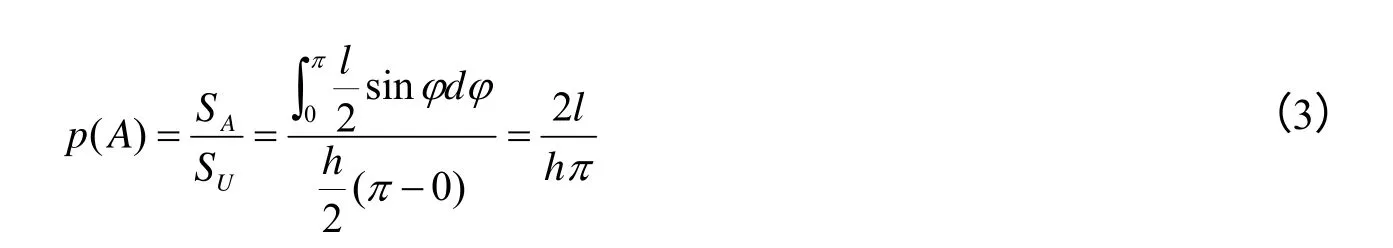
同理，与窗口左边或右边交切记作事件B，则概率P(B)可表示为：

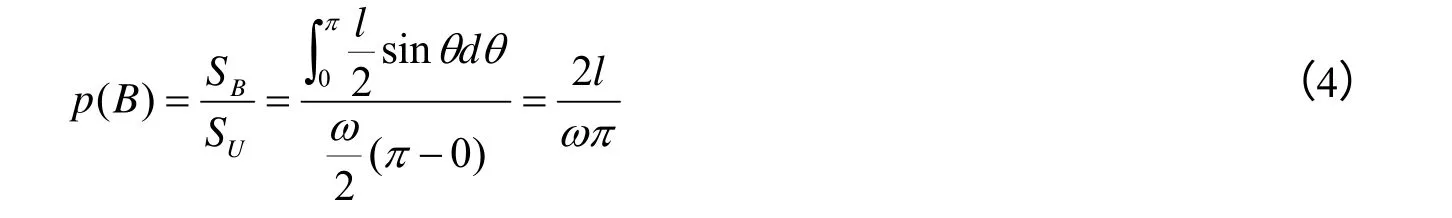
窗口边界被交切的平均频率为：

将P(A)和P(B)代人上式，整理后可得：

上式即为H-H迹长均值估计模型。

1.2 不连续面连通率的估算

根据同样的思路，平均间断长也从H-H迹长均值估计模型的得出，得到锁固段与窗口交切关系及数量就可以估计出平均间断长。两端不可见的迹线在延伸方向与窗口无交切，此时有n0条与窗口不交切的锁固段；一端可见的迹线的延伸方向与窗口有一个交切点，此时有n1条与窗口不交切的锁固段；两端可见的迹线与窗口有两个交切点，此时有2n2条与窗口不交切的锁固段。假设窗口内有n3条两端可见的锁固段，得到与窗口交切关系的锁固段总数为[3]：

利用H-H模型进行平均间断长的估计，可得间断长的公式为：

由连通率定义可知：

将两式代人上式，经整理可得：

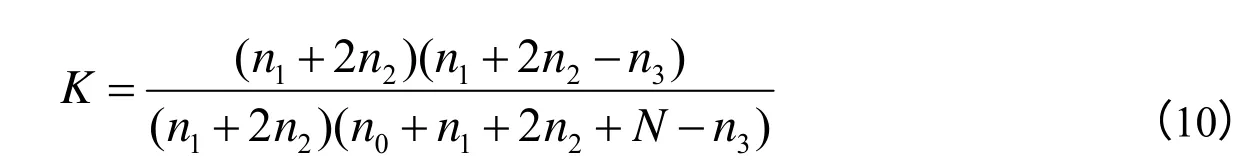
考虑到在实际测量中n3相比N,要小得多，故可令其为0，式(10)简化为：

上式即为不连续面连通率的估算公式。

在实际工程当中，常会出现两种极端情况：其一是取样窗口相对于窗口中最长迹长足够大时，此时有n0=N，n1=n2=0如图2所示；二是取样窗口相对于窗口中不连续面足够小时，此时有n0=n1=0，n2=N，如图3所示[12]。

我们将上述两种情况分别作为第一种情况和第三种情况，介于两者之间的作为第二种情况，根据工程存在的三种不同情来对H-H连通率计算式进行修正，以得到符合工程实际的连通率。

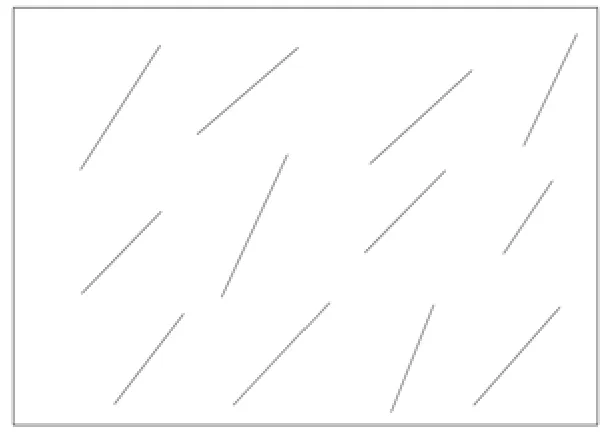
图2 两端不可见迹线

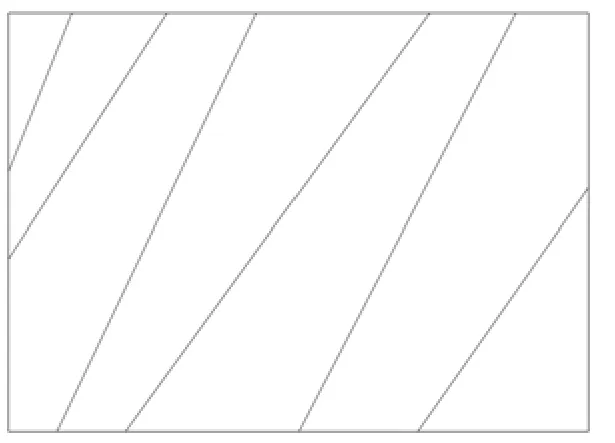
图3 两端可见迹线

第一种情况：由于取样窗口相对于窗口中的不连续面足够大，此时，两端都交切以及只有一端交切的迹线均为0，在这种情况下根据H-H迹长均值估计模型和不连续面连通率的估算公式计算出的平均迹长和连通率均为0,这不符合实际情况。鉴于此，以下给出第一种情况下连通率修正估算式：

式中：l′为修正后的平均迹长，按下式计算：

式中：lj为窗口中包含的不连续面的实测均值。

第二种情况：可直接采用式(12)计算。

第三种情况：由于取样窗口相对于窗口中的不连续面尺寸较小，不连续面都与取样窗口相交切；在这种情况下根据不连续面连通率的估算公式计算出的连通率为1,不符合实际情况。有必要对该情形下连通率进行修正。由陈剑平[11]对n0，n1和n2的数量占N比例的情况讨论，对于不同情况下的平均迹长做了修正，其中，R0,R1,R2分别为n0，n1和n2的数量占N的比例。在此基础上，我们按如下方法修正：

R0＜10%，R1＜10%时，采用公式（13）修正；

R0＜10%，10%＜R1＜40%时，采用如下公式进行计算；

上式中，l′为修正后的平均迹长，计算公式如下：

R0＜10%，R1＞40%时，采用如下公式进行计算；

上式中，l′为修正后的平均迹长，计算公式如下：

R0＞10%，R1＜10%时，采用（14）进行修正；

R0＞10%，R1＞10%时，采用（12）进行计算。

以上给出了本文完整的连通率修正计算式，下文将开展实际验算，以检验修正是否合理。

图4 部分平硐裂隙图（PDJ02）

2 实例

以某水电站平硐裂隙实测数据为例（图4），该地区岩性构成多为英安岩，发育随机的不连续结构面，我们取选取多个平硐的左壁作为研究区，窗口高为2m，长为100m。通过Dips软件分析得到多组优势结构面，进而进行验证（图5，图6）。考虑到工程实际中对边坡稳定性的影响起主导作用的为倾坡外的不连续结构面，故右表中给出了倾坡外优势结构面的基本参数及未修正连通率计算结果和修正后的结果[13]，通过两种计算结果的对比，既验证了不同情况下各修正公式的正确性，又得到了与工程实际相符的连通率。