微积分教学中融合课程思政路径探索

罗 琳

(上海第二工业大学 文理学部,上海201209)

0 引言

习近平总书记在全国高校思想政治工作会议上强调要把立德树人作为高等教育的中心环节,把思想政治工作贯穿教育教学全过程, 实现全程育人、全方位育人[1]。微积分作为一门通识基础课,是大学生进校第一年的课程。它具有课时多、知识量大、逻辑性强、覆盖面广的特点, 又是后续专业课程学习的重要基础。可以说这门课程的学习关系到学生大学4 年学习习惯的养成和学习自信心的建立,也是培养学生坚定的文化自信的基础。那么, 作为一名高校数学教师,如何顺应时代的要求做好微积分课程教学中的课程思政？把思政工作润物细无声地浸入到微积分课堂教学中,实现微积分课堂教学中的全程育人、全方位育人, 体现课堂教学中的立德树人思想,培养学生正确的人生观、价值观和世界观,这就是我们现阶段急需认真思考并积极探索的课题。近年来在新工科背景下, 大学生的专业课堂教学与课程思政的有机结合也深深吸引着广大教育工作者,人们都在关注新工科背景下高等院校改革发展路径,探索专业教学中渗入课程思政教育的理念和路径,并开展多种多样的教学改革尝试[2-11]。如：刘淑芹[4]强调：课程教学的第一要务是立德树人,要充分挖掘蕴含在专业知识中的德育元素,实现通识课与德育的有机结合。刘向娇[10]强调：通过对教材中所包含的知识点和思想要点的结合,对教学大纲修改等教学设计和方法的改革,将思政教育充分融入到课程教学中。本文主要就以下3 方面开展微积分课程教学中融合课程思政的路径探索。

1 根据课程特点, 找准教学问题、做好顶层设计

微积分课程特点主要表现为：内容抽象、逻辑严密。教师在教学过程中常常绞尽脑汁,希望把复杂的问题简单化、抽象的问题具体化。但相当一部分学生在学习过程中依然困惑重重、一知半解,甚至变现出前后知识不连贯, 时间一长, 困难累积越多, 最终导致厌学情绪及谈微积分色变的心理。进一步还会影响学生对其他后续课程的学习信心,甚至影响他们人生观、世界观、价值观的形成。鉴于出现的这些问题,教师在教授这门课程之前就要做好课程教学的顶层设计,发挥课程思政在课堂教学中的灵魂作用。教育的本质就是坚持“以人为本”的理念,培养学生自觉自愿的学习,而不是被动地应付各种各样的考试。而且大学4 年是一个人人生观、世界观、价值观形成的关键时期,对学生今后的发展具有非常重要的影响。为了帮助学生树立正确的人生观、价值观和世界观, 克服微积分课程学习思想上的畏难情绪,教师课前可以做好顶层设计,比如课前做一些微积分发展简史的介绍,让学生充分了解17 世纪英国数学家、物理学家牛顿和德国数学家、哲学家莱布尼兹创立微积分所做出的巨大贡献。正是由于微积分这门课程的横空出世,迅速催生了一系列新的数学分支和其他学科如物理学、天文学的快速发展。由此引导学生向科学前辈学习,激发他们勤奋好学、奋起直追的求知欲望。现如今,随着大数据时代的扑面而来,微积分及其催生出来的数学学科依然是大数据时代的核心技术。比如我国著名的IT 公司华为技术有限公司,公司创始人任正非在多次受访中都强调基础学科的重要性,尤其是数学学科。华为的研发中心拥有700 多位数学家, 数学在一家高科技公司中的重要作用可见一斑。作为数学教师,可以自豪地对学生说：数学学科依然是催生其他学科的灵魂学科,好好学习数学吧,看看我们的华为！从而提高学生对学好数学基础课程“微积分” 的紧迫性和责任感, 培养学生的爱国热情和民族情怀。

2 根据学习现状,统一思想认识,做好全程育人

习近平总书记强调思想政治工作绝不能单纯一条线,不能跟专业教育搞成两张皮,要加强嵌入式、融入式、渗透式教育,把思想政治教育跟专业教育紧密联系起来。因此,在课堂教学方面,教师首先要统一思想认识, 做好教育教学的全过程育人。在管理制度上,特别制定了微积分课程的教考分离制度和微积分课程过程考核实施方案。从管理制度上、从学习过程中杜绝了学生营私舞弊、考前突击的侥幸心理, 引导学生树立正确的学习观、成才观。同时,可以将思想政治表现和道德情操的考核纳入学生平时成绩的一部分, 实现全过程全方位育人。其次,我校为了深入贯彻全员育人的精神,选择责任感强的专业教师担任学生的学业导师,每年评选优秀学业导师、我心目中的好老师、三全育人标兵等,鼓励教师爱岗敬业、做学生灵魂的工程师。教师坚持课堂教学过程育人,特别强调在课堂教学中,思想政治教育要做到自然、贴切、生动、深刻,坚决杜绝庸俗化、牵强附会和流于形式。以渗透为主,“随风潜入夜,润物细无声”,立德树人与传授知识融于一体。立足课程知识,借助实际问题,挖掘辩证思想,循循善诱,以理服人。使学生在学到知识的同时,树立正确的人生观和价值观。

3 根据教学内容, 精心内容设计、做好案例教学

学习知识的最终目的都是为了应用知识解决实际问题。微积分课程知识更是在实际应用中无处不在。比如在微积分课程体系中, 导数的应用是一个重要的知识内容,它涉及到函数单调性和凹凸性,也就是函数曲线的弯曲与走向。在讲解函数单调性和极值时教师可以引导学生联想一些实际问题也是这样的发展过程,比如一个运动员的职业生涯,首先是通过教练的指导和自己的刻苦训练,各方面的技能越来越好,成绩不断的超越自己,满意度呈现上升的趋势。随着年龄的增长, 当运动员各方面的技能和体能达到顶峰过后,这种巅峰状态会有一个逐步回落的过程,慢慢趋向平稳状态。正所谓运动有巅峰、人生有起伏。引导学生正确对待学习中、工作中的得与失,从而树立正确的人生观和价值观。在讲解曲线的凹凸性时,可以把曲线的弯弯曲曲比喻成人生的道路,鼓励学生要有一颗坚定淡然的心,把人生拐点当作必经的驿站,在曲折中前进、在前进中发展。

实际问题的研究通常表现为建立模型、解决模型。建立模型的数学表现形式通常为建立方程。非线性方程的求解过程通常是很困难的,有的问题甚至无法找到精确解答, 好在实际应用中, 通常不需要知道方程的精准答案,只要找到方程的近似解就能达到解决实际问题的目的。例如：工厂生产某大型激光产品, 考虑到综合方面的因素, 产品的销售收入定为多项式函数R(x) = x3+1.1x2+0.9x(其中,x 表示该产品售价,单位：万美元),其中厂房每年的租金和水电是1.4 万美元。问当产品售价不低于多少时(误差不超过10−3),工厂每年的生产能够正常运转(暂不计人工费用)? 在讲解该问题时,首先要建立模型: 即维持工厂生产正常运转的利润函数是p(x) = x3+1.1x2+0.9x −1.4。很显然这是一个严格递增函数, 也就是说, 要使工厂生产正常运转, 当我们确定了产品价格x 时, 产品收入R(x)=x3+1.1x2+0.9x 起码需要付得起厂房租金和水电,也就是求解下列方程模型的近似解：

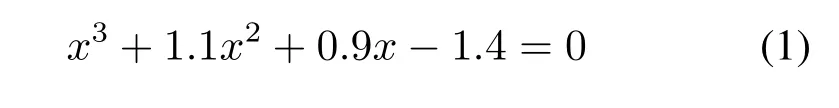
可以看到这是一个标准的三次多项式方程,在实数范围内很难求出其精确解,没有类似于二次方程那样简单直接的求根公式,虽然有卡尔丹公式法或盛金公式法, 但具体操作起来不方便。而该问题不需要求出方程的精确解,只要求出其近似解就够了。那么,可以利用导数的应用中切线法求解如下：

由于p(0)<0,p(1)>0,p(x)>0,根据闭区间上连续函数的性质知道,方程在[0,1]之间存在唯一解0 < ξ < 1。因此可以选择[0,1]作为方程根的一个隔离区间(注：隔离区间就是指方程的近似解一定在此区间的内部取得)。

在[0,1] 之 间, p(x) = 3x2+ 2.2x + 0.9 >0,p(x) = 6x+2.2 > 0。所以按照p"(x) 与p(1)同号的切线法原理,可令起始根为x0=1,再连续应用根的近似值递推公式得到根序列：

而p(0.670) < 0,p(0.671) > 0, 由闭区间上连续函数的性质知, 方程(1) 的唯一精确解ξ 必满足不等式：0.670<ξ <0.671。因此可以用0.670 或者0.671作为该方程的近似解,其误差都小于10−3。

这一近似解的求解过程只用了4 步递推运算就实现了,如果将误差范围缩小,则需要更多的步骤。实际上有些工程问题我们需要几十甚至几百步递推运算才能获得我们最初想要的结果。通过这一实际问题的计算过程,教师可以自然地引导学生学习习近平总书记提出的“不忘初心、牢记使命” 的讲话精神。对于该问题,求误差小于10−3近似解就是最初的想法,后面的4 步是围绕这一想法的不懈努力。做实际问题是这样,做人也是这样,我们每个人都有自己的初心。有的人的初心比较容易实现; 有的人的初心需要披荆斩棘、拼搏奋斗,才能绽放,然而一旦绽放,就会光芒万丈。例如,国民才女武亦姝,2017 年在“中国诗词大会”上获得的骄人成绩源自她从小到大对中国诗词的喜爱,对中华文化的自信,才能十几年如一日努力学习,不断积累。所以,我们的未来在一定程度上是由我们的初心决定的。借此机会鼓励学生要树立当代大学生的信念,坚持自己的初心,不断在大学的海洋里深造,在图书馆的知识宝库里遨游,在实验室、实训基地里磨练,在人生的道路上不断砥砺前行,才能成为时代的开拓者,才能实现中华民族伟大复兴的中国梦。

4 结 语

微积分课程思政实施的关键在于教师的引导,教师要坚持以学生发展、学生成才为中心, 做好顶层设计、实施全程育人。应根据课程内容, 精心设计,做好案例教学。数学知识本身是枯燥的,尤其是高等数学知识更加抽象、严密。所以恰当融入思政教育,常常会给课堂教学带来一份生动感、趣味感，从而提高学生的学习积极性。因此教师要不断提高自身的思政理论文化修养,正确处理教师的“教”与学生的“学”的关系,爱岗敬业、热爱课堂,在教育教学中体会培养学生的成就感、在教书育人中获得幸福感。教师的语言和行动潜移默化地影响着学生的身心发展,在教学过程中学生不仅学习了数学理论知识, 而且在潜移默化中树立了正确的人生观、价值观和世界观, 成长为德才兼备、全面发展的新时代应用型人才。