数字图像相关中的散斑区域自动提取研究

胡慧然，但西佐，赵琪涵，孙方圆，王永红

(合肥工业大学 仪器科学与光电工程学院，安徽 合肥 230009)

1 引 言

数字图像相关方法(Digital Image Correlation,DIC)由于具有非接触、系统组成简单、全场测量等优点在众多领域中的应用越来越广泛[1-5]。DIC是基于数字图像处理的一种全场变形测量技术，其基本原理是选取变形前感兴趣的像素点的灰度子区，通过相关计算，跟踪变形后感兴趣点的位移变化。全场计算时，需要对每个感兴趣区域的种子点进行整像素或者亚像素匹配以达到全场测量的目的[6]。为了确保测量点变形前后的唯一性以及测量结果的准确性，一般测量前需要对被测物或被测区域随机喷涂两种或多种颜色差异较大的涂料形成散斑[7]。如文献[1]中提到在高温测量下不同温度段最优成像对应的散斑图样。文献[4]人车碰撞实验中会对撞击物与车前盖喷涂黑白散斑，利用DIC方法计算碰撞后的头部伤害指数(HIC)。

由于DIC的计算效率受到测量点个数的影响，测量点个数越多，精度越高，但所花费的时间也越长。如果不事先选择散斑区域约束计算点的范围，会产生很多无用结果，浪费了大量的计算时间，而且在实际拍摄的图像中散斑区域一般只占图像的一部分。长期以来，国内外学者在实验过程中往往会人工选择散斑区域并设定一个种子点进行计算[8]，目的是限制相关搜索范围以减少计算点的数量，但面对大量不同的测量图片以及复杂的轮廓，手动选取散斑区域无疑增加了时间成本和人工成本。近几年散斑质量评价方法得到广泛研究[9-10]，但目前提出的散斑评价方法前提都是整幅图像全是散斑，而在实际应用中，由于背景的影响，直接对图片进行散斑质量评价显然不再适用。在其他研究领域仍以抑制散斑为主要研究课题[11-13]。在DIC测量中实现图像散斑区域的自动提取显得尤为重要。这有助于提升DIC的应用效果及实现DIC自动化。

为了实现DIC散斑区域的自动提取，本文通过分析散斑区域特征，对比常用的边缘检测算法，提出了一种二阶梯度熵函数用于实现对散斑区域的判别，并根据设定的连通区域获取真正的散斑区域。最后通过实验拍摄的散斑图像来验证该方法的有效性。

2 基本原理

DIC散斑区域的自动提取方法相当于一种特征提取技术，散斑区域即所需要提取的区域，散斑区域具有以下几个明显特征：(1)散斑区域内的像素点周围子区灰度梯度大；(2)散斑区域子区内最大灰度值与最小灰度值差值较大；在图像上该特征的表现方式是散斑对比度明显，并具有随机的灰度分布特征；(3)散斑区域内的点构成的区域具有连通性，即符合(1)(2)特征的像素点并不是孤立的点，在周围必定有相似的像素点分布。利用上述3个特征，可以将非散斑区域与散斑区域进行分割。

在图像特征提取中，常用的边缘检测算子一般分为3类：一阶梯度算子、二阶梯度算子与多级检测算子[14]。代表类型有Sobel算子、Laplacian算子与Canny算子。通过分析散斑区域的特征不难发现，散斑区域内的灰度变化曲线非常陡峭，对所有边缘检测算子都很敏感，所以不能通过边缘检测算子对散斑区域直接进行分割。图1(a)为一张复杂背景下的散斑原始图像。灰度均匀变化的背景，经过一阶梯度算子计算的结果如图1(b)所示。可见，其不能很好地将散斑区域与背景区域分离，结果不能让人满意；多级检测的Canny算子计算的结果如图1(c)所示，其通过调节高阈值与低阈值可以很好地消除图片背景的伪边缘，但是由于对边缘过于敏感，且最终输出图片的形式为二值化，不仅没有消除背景带来的影响，还将散斑的特征减弱了;而经过二阶梯度算子计算的结果如图1(d)所示，消除了部分背景的影响，将图像灰度值转为梯度值，适合用作散斑提取前的预处理。

图1 几种边缘检测算子处理结果对比 Fig.1 Comparison of processing results from several edge detection operators

本文用拉普拉斯算子处理采集到的散斑图像，目的是保留散斑区域的特征，剔除背景的影响。拉普拉斯算子是二阶梯度算子，对于连续可微的图像灰度函数或曲面f(x,y)而言，其Laplacian图像g(x,y)定义为：

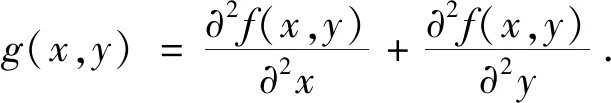
(1)

在数字图像中，图像像素点以离散形式表达为：

g(x,y)=|f(x+1,y)+f(x-1,y)+

f(x,y+1)+f(x,y-1)-4f(x,y)| ，

(2)

式中，f(x,y)代表图片离散坐标(x,y)处的灰度值，g(x,y)代表利用拉普拉斯算子预处理过后对该坐标重新赋予的灰度值。从上述的表达式可以看出，如果图像中像素点的灰度值与相邻像素点的灰度均值间的差值越大，则该点灰度值会越大，即通过拉普拉斯算子处理后，会基本保留图像边缘与灰度值跳跃明显的区域。如图2所示，在散斑区域和背景区域中各取一部分，统计拉式变换前后的灰度直方图。在灰度直方图中可以直观看出，利用该算子进行图像预处理，处理前后散斑区域的灰度分布几乎保持不变，而背景区域灰度分布从0～175缩小至0～40。

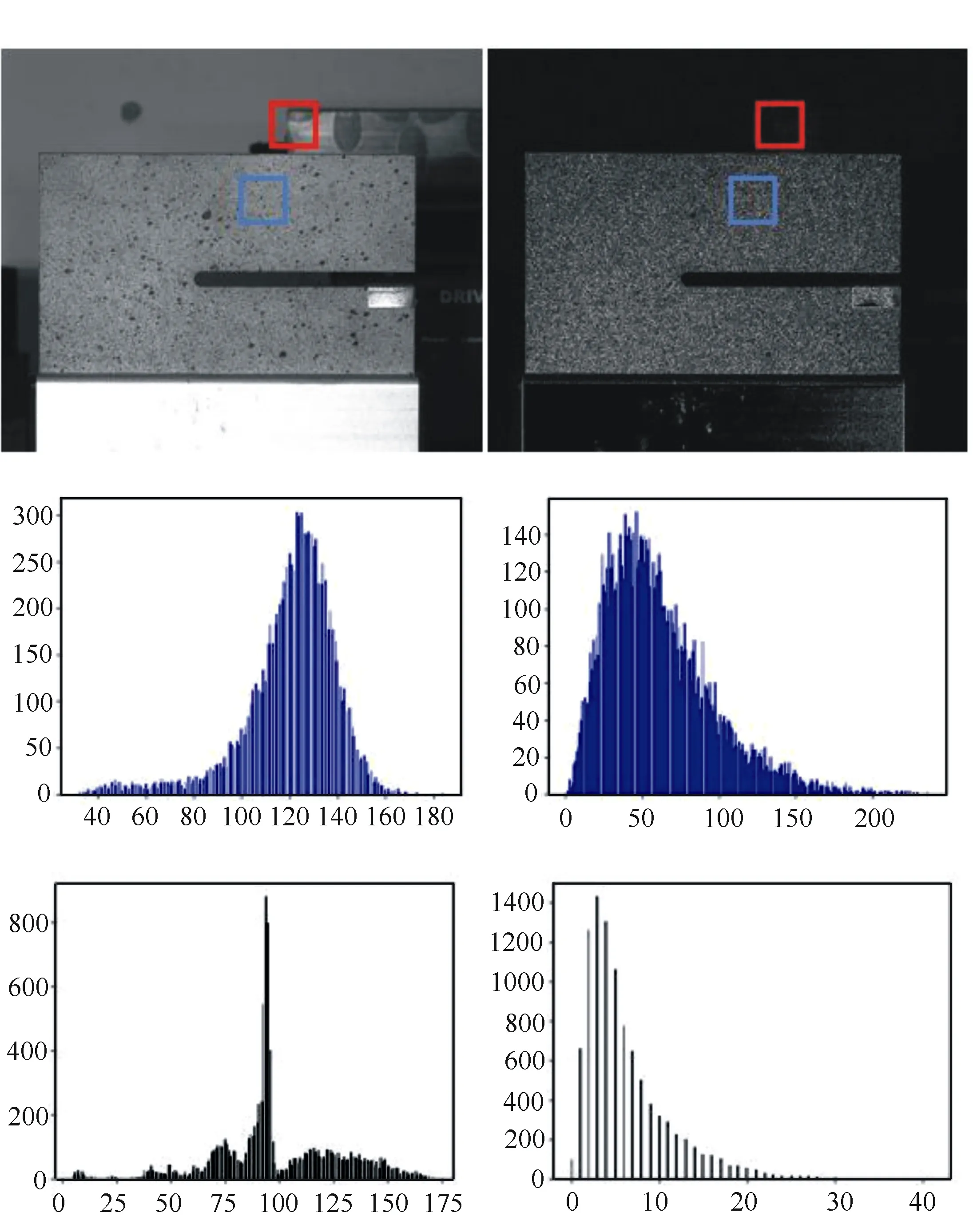
图2 拉式变换后散斑区域与背景区域灰度直方图的对比 Fig.2 Comparison of gray histograms between speckle area and background area after laplacian transformation

由于散斑区域较其他区域的特征对比度更高，灰度分布更广，所包含的信息更多。以点(x,y)为中心的一定邻域内，散斑判定值Rs(x,y)与散斑信息量Is(x,y)有如式(3)所示关系，可以认为其Rs(x,y)值越大，则该点越符合人们所认知的散斑内的点的要求。

Rs(x,y)=f[Is(x,y)] .

(3)

为了统计散斑所含信息量的大小，本文引入熵的概念。熵一般是指统计混乱的程度，在不同的学科中也引申出了不同的定义，熵的概念最先由Rudolf Clausius提出，并应用在热力学中。后来Shannon第一次将熵的概念引入到信息论中。在信息论中，设xn为信源中的随机变量，其出现的概率设为p(xn)，则定义信源的信息熵为[15]：

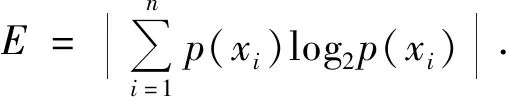
(4)

将熵的概念推广到图像中，即可统计图像信息量的大小,一幅8位BMP图像，设灰度值i出现的概率为ρi,则图像信息熵可定义为：

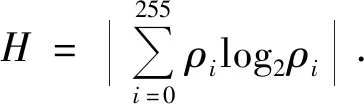
(5)

式(5)反映了图像平均信息量的大小，对于纯黑或纯白的图像，显然图像信息熵值为零，则可以认为图像所带的信息量很小。但是当灰度直方图平稳，即图片中灰度值出现的概率都相等，那么图像信息熵的值相对比较大，此时可以认为图像所含信息量较大。

一个适合用于计算图像信息量的函数应该具有较好的单峰性，较高的灵敏度。基于图像灰度分布的图像信息熵函数虽然能很好地统计出图像信息量的大小，但受实验条件的影响，背景区域的信息量是未知的，因此无法将散斑区域与背景进行有效分离。考虑到图像信息熵这一缺陷，本文从研究散斑特征出发，提出一个适用于提取散斑特征的函数：二阶梯度熵函数QM。消除背景影响，利用QM对图像中的散斑区域进行判定。

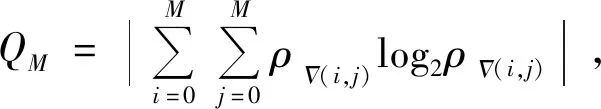
(6)

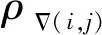
从LQ序列中可以找到最大值Qmax,设定散斑所在的熵值范围处于[Qmax-k,Qmax],当图像中以点(x,y)为中心的邻域对应的二阶梯度熵值Q(x,y)处于[Qmax-k,Qmax]时，将该点置为1，否则将该点置为零，这样可获得分割后的二值化图像Lb。以图1(a)为例，计算其二阶梯度熵，取k为1.25，得到的二值化图像如图3所示。

图3 二阶梯度熵值分割结果 Fig.3 Second order gradient entropy segmentation results

在二值化图像Lb中，根据数值1所在的区域可获得连通区域的面积数组[S1,S2,…,Sn]，将连通区域的面积从大到小排列，若设定散斑区域个数为N，最终散斑所在的区域为[S1,S2,…,SN]。以图3为例，设定散斑区域数量为1，散斑区域提取结果如图4所示。

图4 散斑区域提取结果 Fig.4 Extraction results of speckle area

综上所述，基于二阶梯度熵函数的散斑区域提取算法实现流程如图5所示。

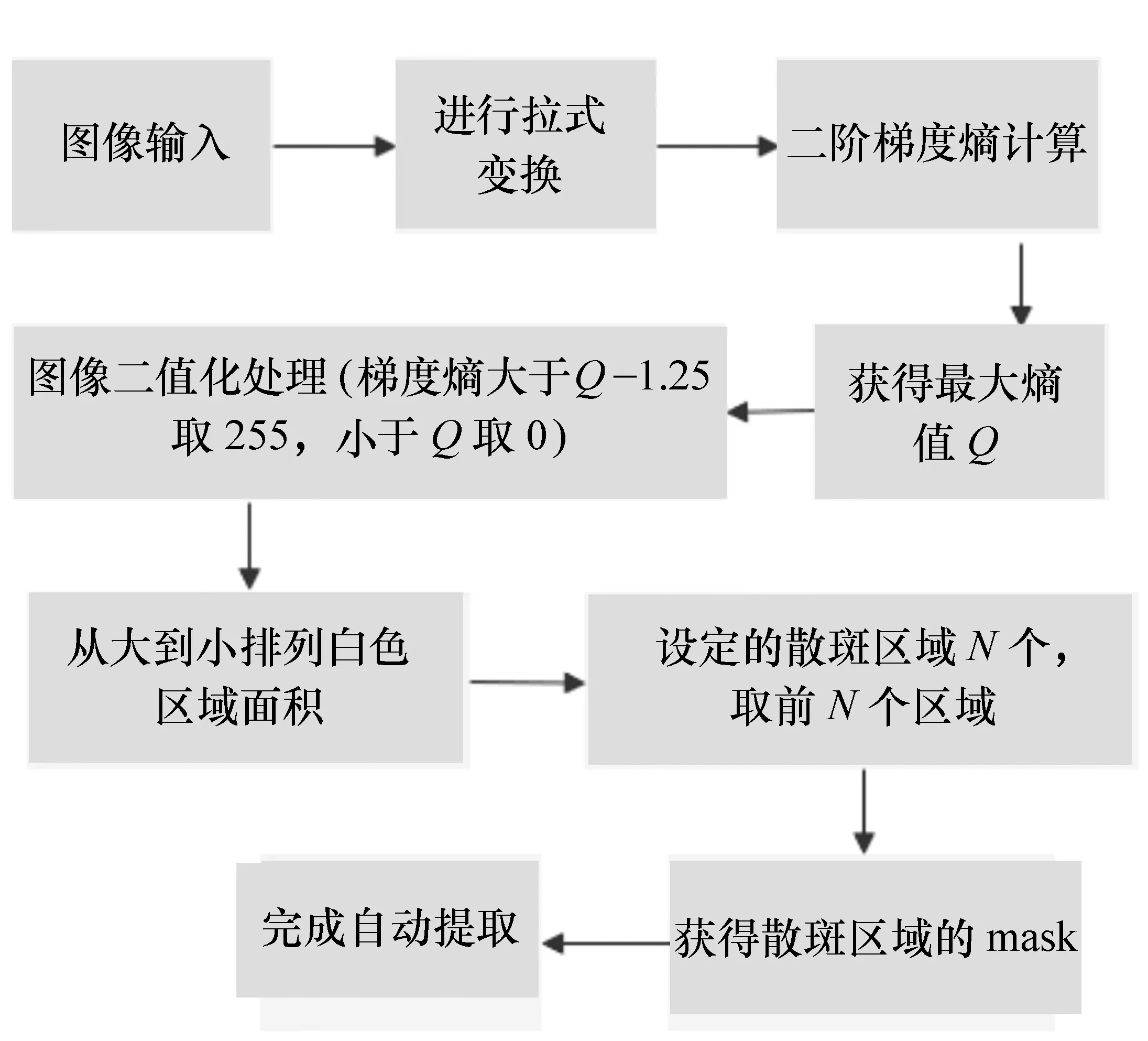
图5 散斑区域提取算法的实现流程图 Fig.5 Implementation flow chart for speckle area extraction algorithm

3 参数确定

3.1 二阶梯度子区熵的求取

对于式(6)提出的二阶梯度熵函数，显然，子区范围越大时，Q值的判定结果越准确，但子区范围过大会导致计算量增加，因此需要确定一个合适的子区范围，既能保证计算速度也能确保结果的准确性。本文利用计算机生成的模拟散斑来对子区大小进行对比分析，模拟散斑生成函数如下[16]：

(7)

其中，s是散斑的个数，a表示为模拟散斑的像素大小，C表示模拟的背景光强，一般设为255，(xn,yn)表示散斑颗粒的位置。

前期有学者认为散斑颗粒尺寸为5个像素是最优的散斑尺寸[17]，因此选取a为5，散斑个数为2 000个，模拟散斑图片的大小为512×512，利用图像信息熵函数(式5)与二阶梯度熵函数(式6)对模拟散斑进行对比实验，方法如下：使计算子区尺寸大小从1个像素增加至50个像素，带入对应的函数计算其熵值，得到的结果如图6(b)、图6(c)所示。

4条数据线分别表示相应大小子区在散斑图中对应函数熵的最大值、平均值、最小值和最大值与最小值的差值。从图6(b)、图6(c)中可以看出当检验子区尺寸小于10个像素时，两个函数对应的熵值最大值与最小值差值较大，散斑区域表现为不敏感，不好准确识别散斑区域，因此不能作为散斑区域判定的尺寸。检验子区增大时，散斑区域对应的熵值最大值与熵值最小值逐渐接近，并且随着子区的增大，熵值最终趋于稳定。如图6(b)所示，虽然随着检验子区的增大，信息熵函数与二阶梯度熵函数变化相同，但二阶梯度熵函数对散斑的感应更加灵敏,如图6(c)所示，当检验子区大小超过10像素时，二阶梯度熵函数几乎是个定值，因此子区大小在10像素至15像素内为最优尺寸。图像信息熵是基于灰度分布的，在实际测量中，背景无法预知，因此传统的图像信息熵函数不符合散斑区域判定的实际应用，这再一次证明了二阶梯度熵函数更适用于散斑的判定。

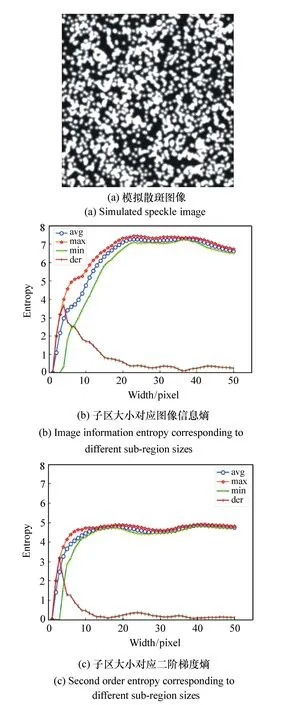
图6 不同熵值随判定子区大小的变化 Fig.6 Different entropy values vary with the size of the decision sub-area

3.2 自适应阈值大小

用于二值化判定的自适应阈值选取是否合理决定了散斑区域提取的准确性，为了确保自适应阈值选取的正确性，本文从具有权威性的DIC Challenge数据库(选择了5幅散斑样式不同的图像确定自适应阈值的范围，如图7所示。将5幅大小不同的图像统一调整为200 pixel×200 pixel，令二阶梯度熵检验子区大小为13,遍历每幅图像，获得二阶梯度熵的最大值、最小值、平均值和最大值与最小值的差值，结果如表1所示。

图7 不同样式散斑图像 Fig.7 Different types of speckle images

从表1可以看出，不同样式的散斑图求得的二阶梯度熵值虽然处在不同区间，但是对于同幅散斑图来说，最大值与最小值的差值在1.25附近(差值均值为1.233 78)，而且二阶梯度熵的最大值与均值的差值小于0.5。这也再次说明，二阶梯度熵函数对于散斑区域的判定比较准确，适合多种不同形式的散斑。在本文后续实验中，自适应阈值取Qmax-1.25，二阶梯度熵值在[Qmax-1.25,Qmax]之间的点认为是散斑区域内的点。

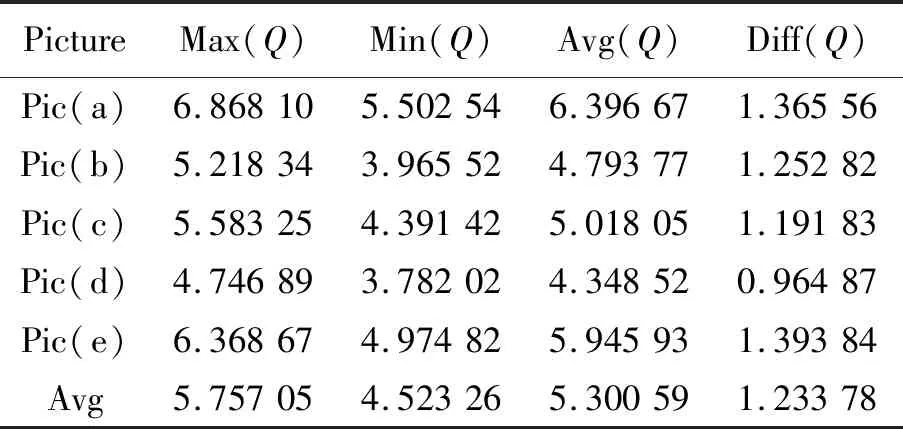
表1 不同样式散斑图对应的二阶梯度熵值

4 实验验证

为了验证本文提出的二阶梯度熵函数对于散斑提取的普适性与有效性，分别对实验室中常用的几种材料喷制散斑或者局部喷制散斑进行实验验证，如图8所示。实验图像包括了一张轮廓比较复杂的试件如图8(a)所示，一张处于复杂背景下的被喷涂散斑的大面积试件如图8(b)所示，一张局部散斑图片如图8(c)所示,以及一张拉伸状态下的散斑图像如图8(d)所示。分别对上述4幅图像根据上述算法步骤进行散斑提取，提取结果如图9(a)、9(b)、9(c)、9(d)所示。

图8 不同的散斑图像 Fig.8 Different speckle images

从图9(彩图见期刊电子版)可以看出，对于散斑喷涂不明显的区域(如图8(b)、图8(c))散斑区域边缘部分可能会有微小的误判。由于光线等原因导致的散斑区域内非散斑区域符合散斑特征也会造成一些微小误判，如图8(d)拉伸棒与被测物的边缘。总体来说，对于正常的散斑区域，本文方法可以较好地提取出散斑所在的区域，基本剔除了散斑未覆盖区域，达到了散斑区域自动提取的效果。

图9 图8中各散斑图像对应的散斑提取结果 Fig.9 Speckle extraction results corresponding to Fig.8

以图8(a)作为原始图，采用第三部分仿真实验的方法，取一处散斑区域与两处背景区域进行对比实验，结果如图10(彩图见期刊电子版)所示。

图10 散斑区域与背景区域对比验证结果 Fig.10 Comparison results of speckle area and background area

可以看出二阶梯度熵函数较好地抑制了背景区域的影响，可以明显区分散斑区域与背景区域，散斑区域的曲线变化也符合仿真部分的曲线，证明了仿真结果的有效性。

5 结 论

本文运用拉普拉斯算子对图像进行预处理，以消除背景的影响，利用提出的二阶梯度熵函数作为子区判定依据，最终通过连通区域数量与大小确定散斑区域所在的位置。通过模拟散斑图与不同样式散斑得出，子区熵尺寸大小在10～15 pixel为最优尺寸，自适应阈值区间定义为[Qmax-1.25,Qmax]。对实际拍摄的图像进行验证，从提取结果可以看出该方法可以较好地提取出散斑所覆盖的区域，为后续的相关计算给出了有效区域，可以为人工选取提供参考或逐步代替人工选取。