椭圆偏振光谱测量技术及其在薄膜材料研究中的应用
2020-01-10朱绪丹张荣君郑玉祥王松有陈良尧
朱绪丹,张荣君,郑玉祥,王松有,陈良尧
(复旦大学 信息科学与工程学院光科学与工程系,上海 200433)
1 引 言
现代电子集成电路是由不同的材料,按照不同的图形设计构成的复杂三维结构。更小体积的器件和更快的运行速度是其设计的核心,而这要求单个电路元件的尺寸能够做得更小,同时每块芯片能实现更多的功能。器件的制造是通过一系列精确控制的加工工艺完成的,为了保证每步工序都能正确地进行,在每一个工艺步骤中都有许多测量和监控技术,其中光学测量由于其非接触、无破坏、无污染的特点被广泛使用。除工业生产之外,光学测量技术在科学研究、技术开发、医疗卫生、国家安全等领域都具有不可或缺的作用[1]。
光学测量的一项重要内容是薄膜特性——例如厚度和光学性质。常用的光学测量技术根据其原理可分为:光吸收法、干涉监控法、偏振光分析法等[2-3]。其中偏振光分析法就是本文介绍的椭圆偏振光谱测量技术(后文中简称为椭偏,本文介绍的椭偏仪/椭偏技术均采用反射式),该方法是利用偏振光在材料表面反射后,相应偏振态的改变来测量该材料的光学性质。通过椭偏测试,可以获得材料的折射率、消光系数和复介电函数等光学性质,还可以进一步计算得到包括材料反射率、吸收率、透射率、光学带隙在内的相关光学特性。同时,椭偏技术还可用于获取材料组分、界面层性质和粗糙度等综合信息。
与其他光学测量技术相比,由于椭偏技术是通过采集反射后偏振光的振幅比和相位差等信息进行测量,因此能够达到更高的精度,故适宜于研究材料的表面与界面性质。在目前半导体工业中,椭偏技术作为一种快速、高精度、非破坏(或干扰)性的膜厚和结构测量手段受到了广泛应用[4]。同时,椭偏技术可以测量和分析多层膜结构、纵向分布不均匀样品、多组元材料等许多复杂体系。此外,椭偏光也受到双折射晶体和材料应力的影响,因此也能够用于研究双折射现象、各向异性或者应变产生的一些光学现象。这一特性在结构和机械工程学中也获得广泛应用。可见,开展对椭偏技术的研究和应用对多种材料的光学、电学、力学、结构(多层结构)、化学组分等多方面综合信息的获得具有重要意义。
本文首先叙述了椭偏技术的发展历程。介绍了传统椭偏光谱测试仪(简称椭偏仪)的结构及原理,接着介绍了一些常用的椭偏仪,包括:结构、原理、优缺点和应用。其中重点介绍了复旦大学研制的双重傅里叶变换红外椭偏光谱系统。然后归纳了椭偏参数(ψ,Δ)处理的方法及步骤,整理了数据拟合常用的光学色散模型,并分别列举了具体应用实例。最后总结并展望了椭偏分析技术未来的一些发展方向。
2 椭偏技术的发展历程
椭偏的概念首先由德国科学家Paul Drude在19世纪末提出,1887年他使用Fresnel公式解释了以布儒斯特角射入水中的偏振光,反射得到的p偏振光反射率不趋于0的问题[5]。Drude不仅仅给出了椭偏分析的理论基础,1890年他还使用该方法测得了18种金属的光学性质[6]。随后,有许多科学家开始着手研究椭偏仪器的研制和椭偏测试的应用,有许多重要的研究成果引起了热议。
初期阶段,科学家们主要使用手动消光式椭偏仪,这种椭偏仪结构简单,使用人眼作为探测器,手动完成测试操作和数据处理过程,被称为椭偏的“Dark Ages”[7]。1933年,L. Tronstad将椭偏技术应用于电化学中金属表面薄膜性质的分析[8];1937年C.V.Kent和J.A.Lawson设计出使用反射光偏振态为圆偏振的方法研究了金属的表面性质[7,9]。1945年A.Rothen在他的文章中将该技术命名为“ellipsometry”,即本文介绍的椭偏技术[10];随后W.Budde于1962年设计并发表了第一个旋转检偏器式椭偏仪(Rotating Analyzer Ellipsometer,RAE)[11]。至此关于椭偏技术的研究和论文发表已经具有一定规模。1963年,在美国华盛顿举行了第一次椭偏研讨会,出版了会议论文集[7]。早期的椭偏测量仪器受限于光探测技术和自动化技术的限制,在测量精度、数据采集速度、运算速度和应用领域方面都表现平平。
直到1973年,椭偏技术有了一次重大飞跃,光度式椭偏仪进入人们的视野。这次进步的根本动力来源于计算机技术的发展。小型计算机的发展不仅仅使得数据处理和计算更加快速和简便,大大缩短了一次测试的周期,提高了测试的准确性,避免了人工计算和操作的误差;与此同时,光度数据可以在测试阶段内周期地存储,并且应用于计算,是光度式椭偏仪得以问世的根本保证。1973年,IBM公司的P.S.Hauge和F.H.Dill同Bell实验室的科学家们先后发表了他们的研究成果[7,12],他们设计制造出了一种计算机辅助的椭偏厚度测试仪(Ellipsometric Thickness Analyzer,ETA),该系统运算速度快,完成一个周期测试仅需5 s;准确度高,厚度测量误差为0.1 nm。
首先发展起来的椭偏仪结构主要是旋转检偏器型椭偏仪(Rotating Analyzer Ellipsometer,RAE)、旋转起偏器型椭偏仪(Rotating Polarizer Ellipsometer,RPE)和同时旋转起偏器和检偏器型椭偏仪(Rotating Polarizer and Analyzer Ellipsometer,RAP)3种,但是这几种结构在Δ等于0°和180°处具有较大的误差。1975年,P.S.Hauge和F.H.Dill设计出旋转补偿器型椭偏仪(Rotating Compensator Ellipsometer,RCE)[13],1983年,D.E.Aspnes报道了他使用椭偏技术获得的8种半导体材料的光学常数(入射光子能量范围约为1.5~6.0 eV)[14]。1987年,J.A.Woollam 等获得专利[15],使用多个滤波器实现了多波长的测试。最后出现的是相位调制型(Phase-modulation Ellipsometer,PME)椭偏仪,其中典型为光弹性调制型椭偏仪(Photoelastic Modulator,PEM),PEM型椭偏仪可以实现对样品的准实时测量[16-18]。D.E.Aspnes是椭偏技术发展史上理论方面非常重要的奠基人之一,著有许多重要的文章[19-20]。另一位在椭偏技术实验方面作出重大贡献的学者是R.M.A.Azzam[21-22]。
国内椭偏技术的研究始于20世纪70年代。70年代中期,我国第一台单波长消光椭偏仪TP-75型由中山大学莫党教授等设计并制造[23]。1982年,旋转检偏器式波长扫描光度型椭偏仪(TPP-1型)也得以问世[24]。随后在80年代中后期西安交通大学研制出了激光光源椭偏仪[25],同期实现了椭偏光谱仪的自动化[26]。复旦大学的陈良尧教授于1994年研制出了一种同时旋转起偏器和检偏器的新型全自动椭偏仪[27]。该类型椭偏仪曾成功实现商业化,销售给包括德国在内的多家国内外单位使用。1998年,中国科学院上海技术物理研究所的黄志明和褚君浩院士等人研制出了同时旋转起偏器和检偏器的红外椭圆偏振光谱仪[28]。2000年,中国科学院力学所靳刚研究员研制出了我国第一台椭偏光显微成像仪。该仪器可以实现纳米级测量和对生物分子动态变化及其相互作用进行实时观测[29]。2000年,复旦大学陈良尧和张荣君等人研制出了基于双重傅里叶变换的红外椭偏光谱系统[30]。2014年,华中科技大学的S.Y.Liu(刘世元)教授等人使用穆勒矩阵椭偏仪(Mueller Matrix Ellipsometry,MME)测试了纳米压印光刻(Nanoimprint Lithography,NIL)的抗蚀剂图案[31],同时还检测了该过程中遇到的脚状不对称情况[32],其理论和实验结果都表明MME具有良好的敏感性。近几年,武汉颐光科技有限公司研发生产出宽光谱穆勒矩阵椭偏仪,除了成功使用该椭偏仪进行了OLED屏幕有机发光薄膜镀膜工艺过程的检测外,该椭偏仪还被广泛运用到集成电路、太阳能光伏、化学等领域,并且成功商品化[33]。总体上,我国对于椭偏技术的研究起步虽晚,但是发展迅速,也出现了许多优秀的研究成果。
纵观国内外椭偏仪器的发展史,不难发现,椭偏技术的发展离不开计算机技术和自动化技术的推动。自Drude首次提出椭偏原理(1887年),国内外学者对于椭偏仪器的研究、改进,和椭偏分析技术在不同领域应用的探索就一直保持很高的热情。根据Web of Science的记录,1941年迄今主题中包含“ellipsometry”(椭偏技术)的论文共有31 577篇,论文发表篇数随时间的变化和论文的研究方向统计分别如图1(a)、1(b)所示。
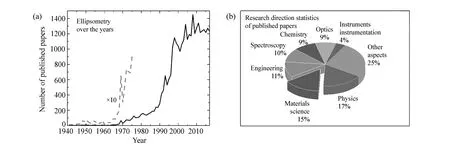
图1 1941年至今主题包含“ellipsometry”(椭偏技术)的论文发表情况统计。(a)论文发表篇数统计,(b)发表论文研究方向统计图。(数据来源:Isi Web of Science) Fig.1 Statistical analysis of published papers with the topic of ‘ellipsometry’ from 1941 to the present. (a)Publication statistics of papers, (b)research direction of published papers. (Source:ISI Web of Science)
从图1(a)论文发表的情况结合椭偏的发展历程,可以发现由于计算机技术在1973年左右的发展与广泛应用,使得椭偏测量更加快速和准确,强有力地推动了椭偏技术的研究,自此之后,论文发表篇数快速增长。其中,研究方向囊括了物理、化学、光学、工程、材料科学和仪器开发等众多方面。椭偏技术在科学研究、工业生产和技术开发等领域都具有不可或缺的作用。
3 椭偏仪测试的基本原理
椭偏仪是测量线偏振光经材料表面反射后,光的相对振幅与相位改变量的仪器,图2展示了椭偏仪的测试基本原理。通过处理测量到的椭偏参数,可以获得所研究材料的光学性质。根据测量方式可以分为反射式、透射式和散射式椭偏测量。其中应用最为广泛的是反射式椭偏测量。
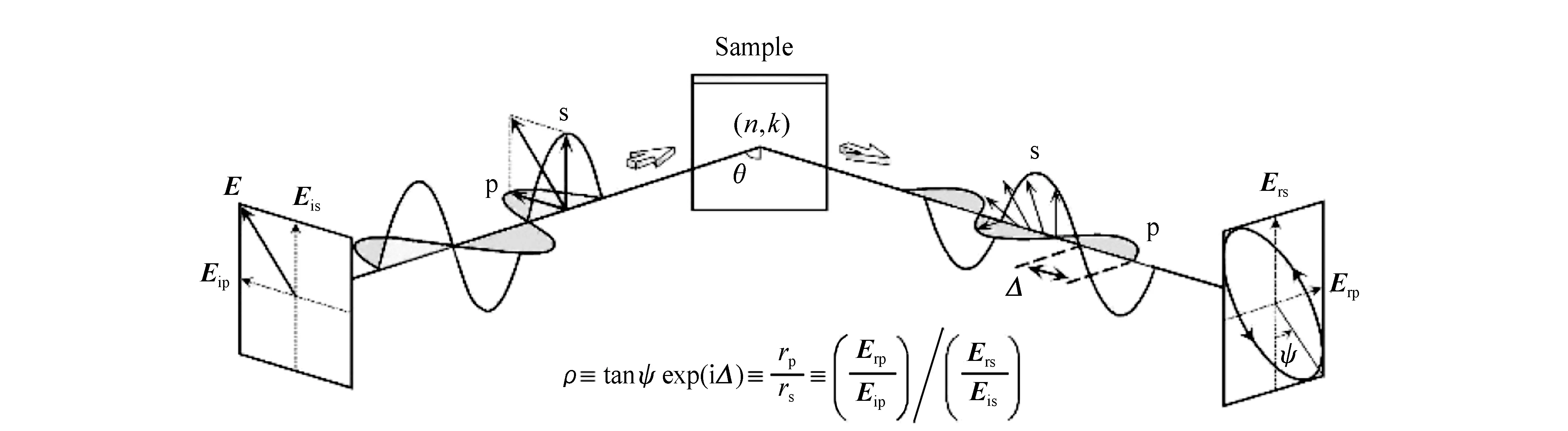
图2 椭偏仪测试原理示意图[34] Fig.2 Measurement principle of ellipsometry[34]
考虑图3所示的理想情况。根据偏振态,将入射线偏振光分解为电场分量偏振方向分别垂直和平行于入射面的s光和p光,两束偏振光相互独立地由复折射率为i的介质向复折射率t的介质传播。光在传播过程中遇到不同介质分界面时会发生反射和折射。
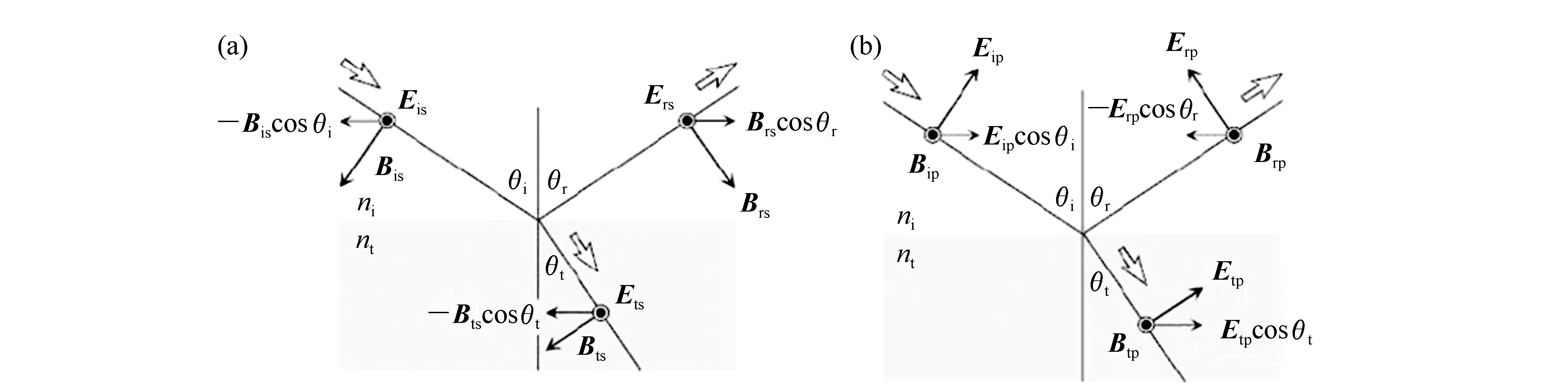
图3 偏振光在介质界面处的反射与折射。(a)s光,(b)p光[34]Fig.3 Reflection and refraction of polarized light at the interface of the medium. (a)s polarization, and (b)p polarization[34]
当s光和p光在两介质界面处发生反射与折射时,其入射角θi、反射角θr和折射角θt之间满足斯涅尔(Snell)定律:
θi=θr,
(1)
(2)
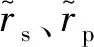

(3)
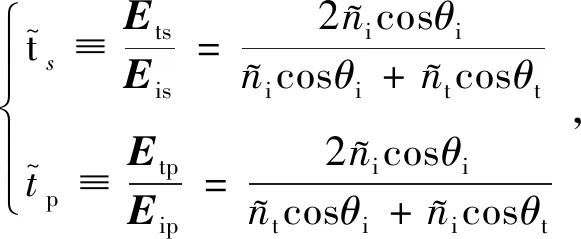
(4)
在反射模式下,定义椭偏参数ψ和Δ,其中tanψ表示p光与s光反射后振幅的比值,ψ的取值范围为0~90°:
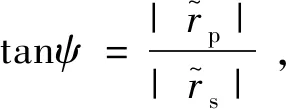
(5)
Δ则表示p光与s光相位差的变化量,Δ的取值范围为-180°~180°(或表示为0°~360°):
Δ=δp-δs,
(6)
椭偏参数ρ的定义式为:
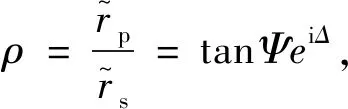
(7)
与此同时,椭偏参数ψ和Δ是入射介质复折射率i、透射材料复折射率t、透射材料厚度d、入射光波长λ和入射角θi的函数:
ψ,Δ=f(i,t,θi,λ,d) .
(8)
使用椭偏仪测试材料的椭偏参数ψ和Δ,再通过计算机辅助计算就可以获得材料的光学常数。具体光学常数(如复介电函数)的计算和数据拟合的步骤将在本文稍后进行介绍。
4 椭偏仪的分类及介绍
椭偏仪按照测试原理的不同,主要分为消光式和光度式两类。本文介绍了PCSA型消光式椭偏仪、旋转偏振器件型椭偏仪、相位调制型椭偏仪、椭偏光谱仪、红外椭偏光谱仪、成像椭偏仪和广义椭偏仪,阐述了不同椭偏仪包括:基本架构、测量原理、优缺点和应用在内的基本信息。
4.1 PCSA型消光式椭偏仪
Drude教授提出椭偏概念的初期阶段称为椭偏研究的“Dark Ages”,因为椭偏测试广泛的应用是消光式椭偏仪[7]。这种椭偏仪结构简单,主要使用单一波长完成测量,并使用人眼作为探测器,测试时需要手动完成各偏振器件角度的调节和定位。典型的消光式椭偏仪结构如图4所示。
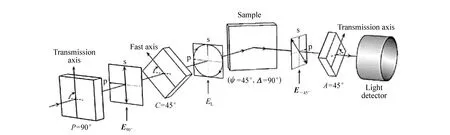
图4 PCSA型消光式椭偏仪结构示意图(图中ψ=45°,Δ=90°,探测器检测此刻为消光状态)[34] Fig.4 Schematic diagram of PCSA null ellipsometry(The (ψ,Δ) values of a sample are assumed to be ψ=45° and Δ=90°. In this measurement, the detected light intensity is zero)[34]
主要由光源、起偏器、补偿器(1/4λ波片)、检偏器和探测器5部分构成。此时由起偏器产生s方向的线偏振光(E90°),通过补偿器后偏振态变为左旋圆偏振光(EL),经样品反射后变为-45°方向偏振的线偏振光,偏振方向与检偏器偏振方向垂直,因此出射光强为零,处于消光状态[34]。其中补偿器只作用于特定波长的光,所以此时仅仅使用单波长的光进行测试。消光式椭偏仪是通过改变起偏器和检偏器的角度使得入射到探测器上的光强值最小(理想状态为消光),由这样一组起偏器和检偏器方位角的数值,就可以求得样品的椭偏参数。由此可见,消光式椭偏仪实际上测量的是角度而不是光通量,这使得光源的稳定性和探测器的非线性所导致的误差较小[37]。同时,其测量精度也主要由偏振器件角度定位的精度决定,有效地减小了系统误差带来的影响,测量比较准确[38]。1945年,Rothen使用消光式椭偏仪测试膜厚的灵敏度已经达到0.03 nm[10]。
虽然测试的准确度较高,但是需要人为地完成偏振器件方位角的调整、读取和计算,影响了测量速度。即使后来使用计算机技术辅助,或者使用光电倍增管等光电探测器,但是对于测试速度并没有显著的改善。反而引入了新的测量误差,例如:光电探测器在光强小时的信噪比较低,这将会增大偏振器件方位角的测量误差[39]。所以消光式椭偏仪主要适用于对测试速度要求不太高的场合,如高校实验室。而在工业应用上主要使用的是光度式椭偏仪。
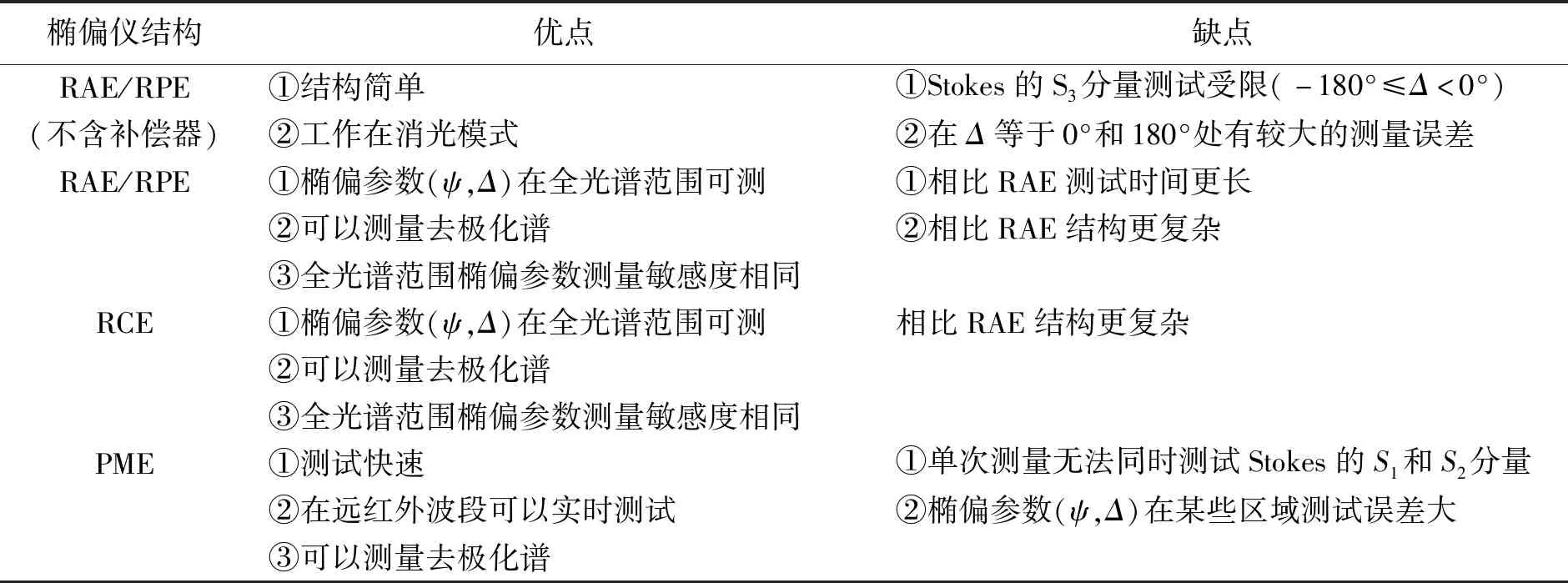
表1 几种光度式椭偏仪优缺点总结[34]
所谓的光度式椭偏仪是指仪器中各个对光偏振态有影响的光学元件,在一定数量恰当的设置状态之下时对光强进行测量的仪器。不同于消光式椭偏仪,光度式椭偏仪更适用于宽光谱的椭偏测试,极大地增加了测量获得的信息量[40]。光度式椭偏仪优势在于:椭偏参数的获取是直接对探测器接收到的光强信号进行傅里叶分析,而不需要测量偏振器件的方位角,所以测量速度明显快于消光式椭偏仪,特别适用于在线检测和实时测量等工业领域。但由于现阶段所能提供的探测器存在非线性效应以及光源的不稳定,都将增大光度式椭偏仪的系统误差[37]。表1总结了几种不同架构的光度式椭偏仪的优缺点[34],其中包含的椭偏仪将在后文详细介绍。
4.2 旋转偏振器件型椭偏仪
旋转偏振器件型椭偏仪包括多种结构的椭偏仪:RAE、RPE、RAP和RCE。在最早的椭偏仪使用中,由于操作简便和成本较低,旋转检偏器(RAE)或起偏器(RPE)的椭偏仪是主导,通过在不同时间获得光强与不同检偏器或起偏器角度之间的变化关系来分析样品数据[41-42]。包括之后出现的同时旋转检偏器和起偏器型椭偏仪(RAP)都是通过偏振器件的机械旋转来完成数据的采集[43-45]。RAE椭偏仪的结构示意图如图5所示。
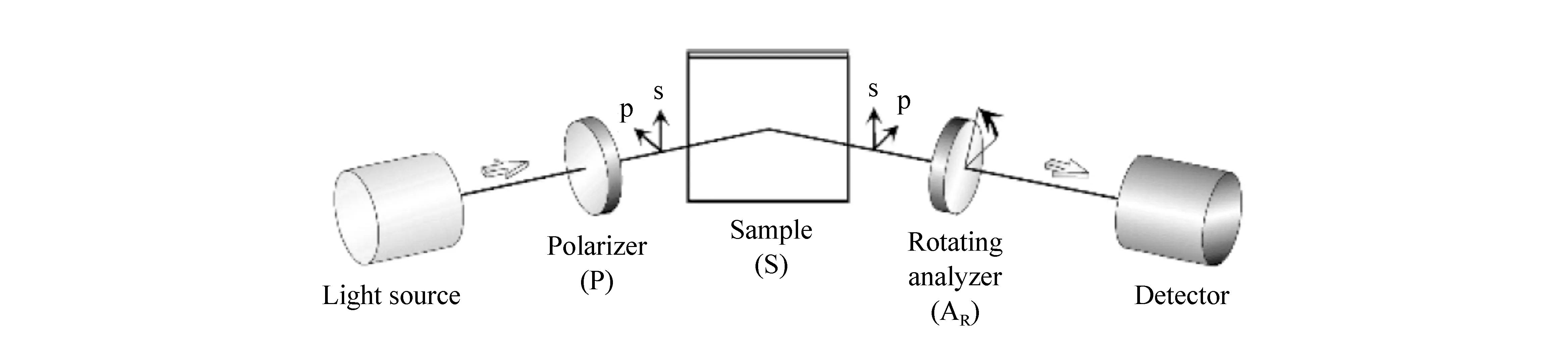
图5 RAE光度式椭偏仪示意图[34] Fig.5 Optical configurations of RAE [34]
RPE、RAP与RAE光学元件配置完全相同,只是在测试时旋转的偏振器件不同。这种测试结构构造简单、技术成熟并且少了1/4λ波片的限制后,更适合于光谱的测量。但是这3种测试结构在椭偏参数Δ等于0°和180°处具有较大的误差,必须加入相应波长的补偿器才能消除[40]。虽然RAE精度较高,但通常易受环境光的影响,测试要求在暗室进行,采用光源调制器和锁相放大器可以解决这一问题。RAP不会受光电流中直流分量的影响,同时可以自动定标。但测试较复杂且光路校正困难,一旦出现光路问题时旋转起偏器就会导致入射光斑在样品表面移动,产生较大的误差[46]。
为了进一步提高测试的准确度,1975年,P.S.Hauge和F.H.Dill设计出旋转补偿器型椭偏仪(RCE)[13],经典RCE椭偏仪的结构如图6所示。

图6 RCE光度式椭偏仪示意图[34] Fig.6 Optical configurations of RCE[34]
RCE在固定起偏器和检偏器的情况下,旋转补偿器可以测试到Stokes矢量的4个分量,消除了RAE、RPE、RAP在椭偏参数Δ等于0°和180°处的误差。如果采用双补偿器旋转,可以测试到Mueller矩阵的所有分量[47],有趣的是,旋转补偿器的思想来源于天文学[48]。这种RCE椭偏仪理论上可以检测任意偏振态(包括完全偏振态和部分偏振态),而且能够测试的样品类型非常广泛,包括各向异性样品,或者粗糙表面的样品。但是使用的补偿器是1/4λ波片,只对单波长有效,使它在多光谱领域中的应用被限制[7,45]。
接下来重点介绍复旦大学研制的双重傅立叶变换红外椭偏光谱系统[30,49]。该系统对光子能量和方位角作了双傅立叶变换,可进行反射式无损测试得到2 100~10 000 cm-1波段样品的各种光学常数,测量误差被控制在了1%以内,测量速度快,对红外光谱区各种金属和合金、窄禁带半导体和超晶格材料等丰富信息的探索具有重要意义。该系统整体的结构示意图和其中RAP型椭偏仪原理图如图7所示。

图7 双重傅立叶变换红外椭偏光谱系统。(a)系统整体结构示意图,1.偏振器;2.分析仪;3.步进电机;4.检测臂旋转平台;5.样品旋转平台;6.样品安装板;7.固定镜;8.移动镜[49],(b)RAP型椭偏仪原理图(其中P和A的方位角相对s轴顺时针旋转)[50] Fig.7 Apparatus configuration of the infrared double-Fourier spectro-ellipsometer. (a)System overall structure diagram,1.polarizer, 2.analyzer, 3.stepping motors, 4.rotating stage of detection arm, 5.rotating stage of sample, 6.sample mounting plate, 7.fixed mirrors, 8.moving mirror[49], (b)optical configuration of the RAP ellipsometric system(in which the azimuthal angles of the rotating P and A are clockwise to the s axis)[50]
如图7所示,该椭偏仪系统采用的是同步旋转检偏和起偏器(RAP)的构造,其中RAP椭偏仪红光光源为15 W的卤素钨灯。该系统并没有使用传统的单色仪分光然后进行波长扫描的方法测试,而是选择通过迈克耳孙干涉仪形成红外傅立叶干涉光源(Necolet 460型IR-FT 产品,采用CaF2分束器和液氮制冷的InSb探测器)图7(b)中的P0,P和A都是偏振器件。P0是固定起偏器,作用是使光源出射的光沿s方向偏振(s向和光入射面垂直);P和A分别是可以旋转的偏振器和检偏器,它们的初始偏振方向都是s向,测试时P和A旋转角速度始终保持1∶2的比例关系同步旋转,方位角分别为θP和θA。
光源出射的光首先通过固定偏振器P0,然后通过起偏器P,以入射角为θ在样品反射后,到达检偏器A,最后进入探测器。根据光学系统琼斯矩阵原理,进入探测器的光的电场矢量可以表示如下[30]:
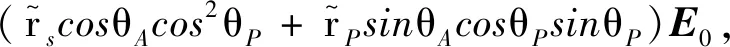
(9)
相应的光强表示为:
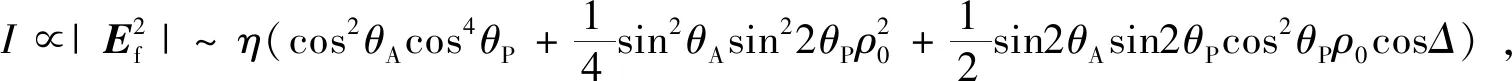
(10)
式中,η为与光强和探测器特征有关的常数,测试时P和A旋转角速度始终保持1∶2的比例关系同步旋转,即方位角满足2θP=θA=ω0t的关系。将光强表示为θA的余弦分频表示式:
I=I0+I1cosω0t+I2cos2ω0t+
I3cos3ω0t+I4cos4ω0t,
(11)
其中包含了5个信号分量,即一个直流分量I0和4个整数倍频的交流分量,各个分量与椭偏参数ρ0(ρ0=tanψ)和cosΔ的关系表示如下:
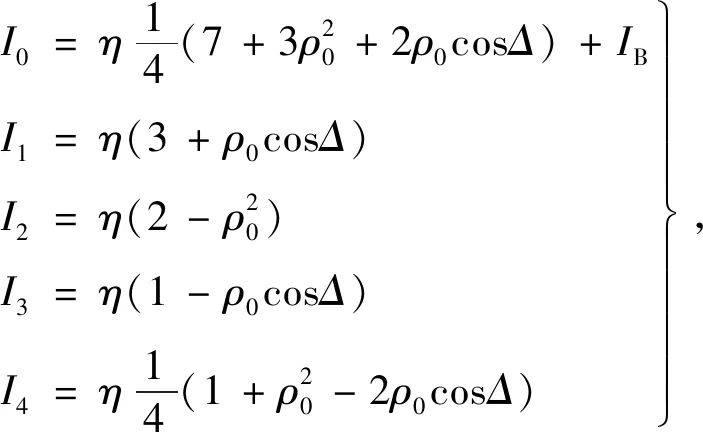
(12)
上式中,IB表示背景信号,则4个方程中只含有3个未知数,故ρ0和cosΔ可用两套独立的方程组表示:
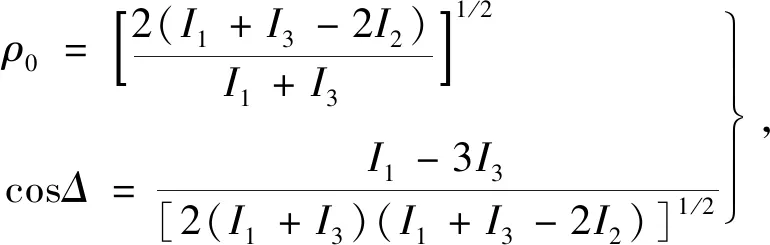
(13)
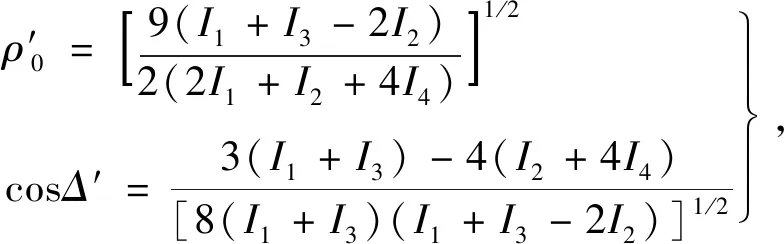
(14)
使用两套计算方式(式(13)和(14))都可以计算得到椭偏参数,并且两套计算结果的符合程度代表了系统自洽度,通过比较计算结果可以知道实验数据测量的可靠程度。自洽度检验也是同步旋转检偏和起偏器方式的特点之一,依据实验结果的自洽度可以对实验数据的精度进行改进[30,49]。
观察式(13)和(14)不难发现,此系统计算椭偏参数,并不需要光强信号的直流分量,只需要对其交流分量进行测试。从而消除了背景光和暗电流等较大的直流本底噪声对测试准确性的影响。同时各交流分频之间的关系一般不会受到红外区存在的水、二氧化碳或其他吸收介质的影响,所以使用上述公式计算得到的椭偏参数基本不会受到这类背景光影响[49]。
4.3 相位调制型椭偏仪
旋转偏振器件型椭偏仪由于测量时都需要旋转部件,这会造成系统的不稳定和方位角的偏差,降低了其测量精度。1969年,S.N.Jasperson等人成功研制出相位调制型(PME)椭偏仪[51]。PME椭偏仪是将图6中的1/4λ波片换成调制器,按预定的方式将光束的偏振态加以调制,从随时间变化的光电流谐变分量中取得样品的有关信息。最典型的是光弹性调制型椭偏仪,其结构如图8所示。
光弹性调制型椭偏仪测试时,向光弹性调制器施加的电压必须根据探测光的波长来改变,以便光通过时获得恒定的相移。所以入射光的偏振态由调制器调制,调制频率与调制器的频率相同。其优点有:首先测量时所有的光学元件都保持静止状态,并不需要机械转动,所以相较旋转偏振器件型椭偏仪测量更加快速。PME测试的最短周期取决于其中压电传感器的频率(50 kHz)[34],所以PME的最短测试周期为20 μs[52];其次,PME已经广泛应用于远红外波段的实时测试。PME的实时光谱测试通过采用光电二极管阵列[53-54]或多个光电倍增管[55]实现。PME的缺点是调制器对环境温度很敏感,因而仪器的稳定性较差。PME实时测量在有些波段是受限的(可见/紫外区域),并且PME误差在(ψ,Δ)特定区域增加[34]。
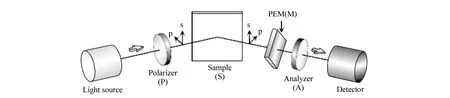
图8 PME光度式椭偏仪示意图[34] Fig.8 Optical configuration of PME[34]
4.4 椭偏光谱仪和红外椭偏光谱仪
椭偏光谱仪可用于测试多层薄膜的光学性质。因为对于多层薄膜中各层光学参数无法直接从一组椭偏参数中求解,考虑到材料的色散性质,即其光学常数随入射光波长的变化而变化,所以需要得到该多层膜结构的多组椭偏参数,这促使椭偏光谱仪得以发展。D.E.Aspnes等在1975年首次基于RAE结构设计出了光谱椭偏仪。该仪器结构如图9所示。
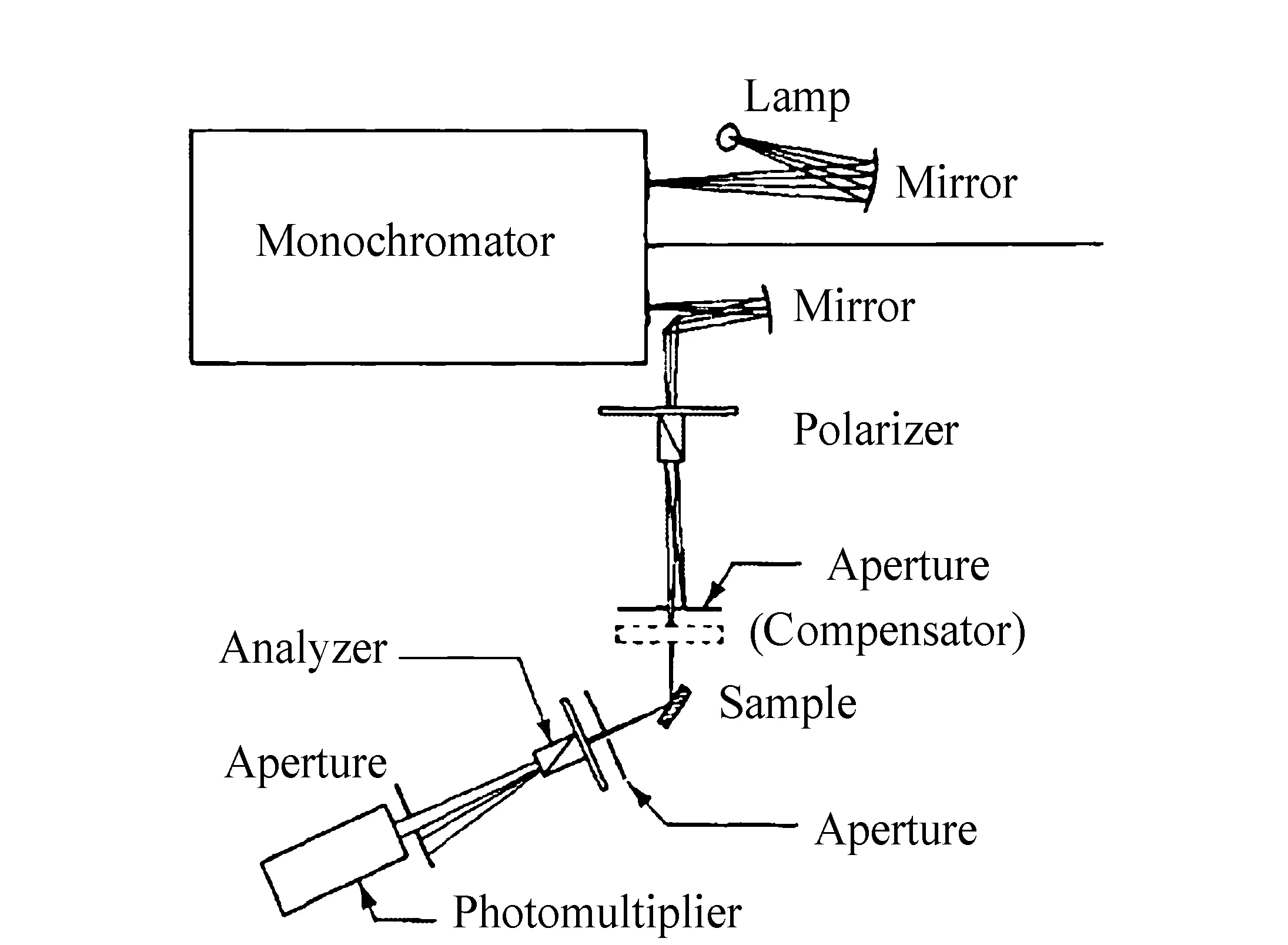
图9 D.E.Aspnes等人设计的椭偏光谱仪结构示意图[56] Fig.9 Schematic diagram of the optical system of the instrument designed by D. E. Aspnes et al.[56]
其中,利用光栅单色仪进行分光,然后通过波长扫描的方法拓宽了椭偏测量的光谱范围(近红外到近紫外),与此同时可以测量高达1 000组的椭偏参量,膜厚的测量精度达到0.001 nm,数据采集周期仅为7 ms[37,56]。在此基础上,红外椭偏光谱仪被广泛运用于半导体行业中异质结构多层膜相关参量的测量。
4.5 成像椭偏仪
椭偏仪在集成电路领域也得到了广泛的应用。但是由于集成电路的特征尺寸小,这对椭偏仪光斑的面积也提出了更高的要求。而传统椭偏仪的光斑面积较大(光斑直径在通常情况下约为1 mm),在集成电路领域中的应用受到了限制。1988年,D.Beaglehole在传统椭偏仪的基础上加入了成像系统,研制出了成像椭偏仪[57]。两者相结合,有效地提高了椭偏仪的空间分辨率。成像椭偏仪利用CCD采集椭偏图像,可以进一步得到样品表面的三维形貌及薄膜厚度分布,从而提供样品的细节信息。而传统椭偏仪只能测量到光斑内薄膜的平均厚度[37-38]。但是成像椭偏仪中样品反射光的偏振态会受到CCD器件的干扰,同时CCD器件有很强的本底信号,使得成像椭偏仪的系统误差因素增多,使用前必须仔细校准[58]。图10展示的是1996年由G.Jin等人设计的成像椭偏仪结构。
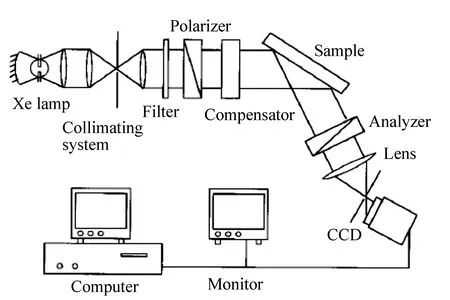
图10 G.Jin等人设计的成像椭偏仪示意图[59] Fig.10 Schematic diagram of an imaging ellipsometer designed by G.Jin et al.[59]
4.6 广义椭偏仪
入射光照射在各向同性介质上时,其s分量和p分量在介质表面的反射和折射都是相互独立的,可以使用传统椭偏仪进行测试。若材料是各向异性的,入射光在反射和折射时其s分量和p分量之间会相互耦合,此时需要使用广义椭偏仪完成测试[38]。
广义椭偏仪的实现途径主要有以下3种[37]:①将旋转偏振器件型椭偏仪拓展到广义椭偏仪,其原理是在偏振器件不同方位角下进行多次测量。M.Schubert和J.A.Woollam等人将RAE拓展到广义椭偏仪,成功地测量了单轴TiO2晶体的复介电函数[60]。②分别在起偏器后和检偏器前放置两块补偿器,并以不同的频率旋转。C.Chen和I.An等人基于此原理设计出了广义椭偏仪,并用于实时测量[61]。③使用具有不同调制频率的两块光弹调制器作为偏振调制器件。此类广义椭偏仪的基础理论是由G.E.Jellison等人提出的[62],他们还研制出了大入射角广义椭偏仪[18]、垂直入射角广义椭偏仪[63]和透射广义椭偏仪[64]。
5 椭偏测试数据的处理
椭偏技术是分析薄膜材料光学性质的一个非常有效的工具。通过对测得的椭偏参数ψ和Δ进行反演计算可以获得包括薄膜厚度、光学常数(包括复介电函数)、表面粗糙度和薄膜内部过渡层性质在内的综合性信息。椭偏技术相比其他表征方法,其准确度更高,尤其对于分析半导体或绝缘体体材料光学性质,当入射光子能量大于材料禁带宽度时,椭偏技术可靠性最高[40]。
但是对于多层膜构成的复杂结构,求解过程就比较复杂,需要为多层膜结构建立相应的光学模型,再结合每层膜的色散性质进行数据拟合,通过调整模型参数使拟合结果和实验数据的误差最小,同时需要考虑所研究膜层的物理性质,最终得到多层膜结构的光学性质。
5.1 体材料椭偏测试数据的处理
体材料的椭偏分析步骤较为简单。可以建立理想的双层介质模型(如图3所示),即两介质均为半无限厚的均匀介质。该情况下,直接将式(3)代入式(7),可得:

(15)
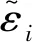
以上就是利用椭偏技术测量表面平整体材料光学常数的原理以及相应复介电函数的计算公式,这是椭偏分析中最简单的情况。1890年,Drude继提出椭偏分析的理论基础之后,使用该方法测得了18种金属的光学性质[6]。除了传统意义上的块材可以使用此种体材料的椭偏参数分析方法,2014年,复旦大学的张冬旭等人在研究锡(Sn)薄膜的光学性质从固相到液相转变时也直接使用式(15)计算了Sn薄膜的光学常数[65]。这是因为Sn材料的吸收系数较高,几十纳米的Sn薄膜即可认为不再透光,所以进行椭圆偏振光谱测量时,光只在薄膜表面反射,相当于半无限厚的体材料,因此直接通过Snell公式和Fresnel公式即可求得Sn薄膜的光学常数,其测量得到的椭偏参数及计算的光学常数如图11所示。
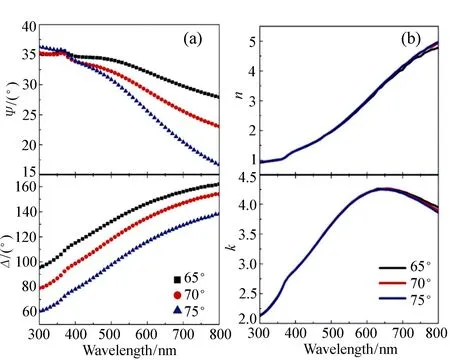
图11 椭圆偏振光谱分析Sn薄膜的光学性质。(a)65°,70°,75°入射时测得的Sn薄膜椭偏参数,(b)Sn薄膜的折射率n和消光系数k与波长的关系[65] Fig.11 Optical properties of Sn thin films studied by spectroscopic ellipsometry. (a)Spectral ellipsometry parameters of Sn films measured at 65°, 70°, and 75° at room temperature, (b)refractive index n and extinction coefficient k of the Sn film vary with wavelength[65]
这种分析方法也可以用来分析各向异性材料。2010年,曼彻斯特大学的V.G.Kravets和A.N.Grigorenko等人使用此Fresnel模型拟合出了制备在具有自然氧化层的硅衬底上石墨材料和石墨烯薄片的复折射率[66]。特别的是,他们将两者视为各向异性材料分别从x向和z向(x轴方向在石墨面内,而与石墨面垂直的方向称为z向)拟合出了对应的光学常数。如图12所示,用此方法拟合x向和z向的光学常数存在一定的耦合现象,并且曲线也不太平滑。因此研究者又使用后文中将介绍的色散模型拟合方法重新拟合,拟合结果将在后文中详细介绍。
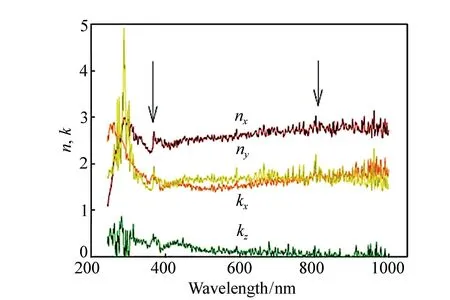
图12 椭圆偏振光谱分析得到的~1 μm厚石墨x向和z向的复折射率(此时z向被认为是普通材料)[66] Fig.12 Complex refractive indexes in the x- and z-directions of ~1 μm thick graphite obtained by ellipsometry(optical constants of graphite with z-component being treated as a general material)[66]
此外,这种体材料的椭偏分析方法在生物材料中也有应用。2004年,德国汉堡大学的B.Schulz和D.Chan等人在使用椭偏技术分析肝组织的光学性质时[67],将肝组织视为均匀的有机生物样品,并且忽略了硅衬底对上层样品光学常数的影响,直接使用体材料的椭偏分析步骤,粗略估计了肝组织的光学常数:n=1.45,k=0.03。由于分析时同时忽略了表面粗糙层的影响,所以测得的k值略高于组织本身的实际值。
5.2 薄膜材料椭偏测试数据的处理
虽然体材料的椭偏分析步骤比较简单,但是在现代椭偏的实际应用中,测量的薄膜材料往往是有限厚度的,材料表面通常也具有一定粗糙度,因此简单地使用体材料的椭偏分析步骤往往不能得到正确的结果。
5.2.1 光学色散模型拟合
对于吸收材料薄膜,需要求解的未知参数包括薄膜厚度,复折射率的实部和虚部,而椭偏参数只有两个:ψ和Δ,则式(8)变成一个无法求解的超越方程。因此,在绝大多数情况下,利用椭圆偏振光谱法分析薄膜材料的光学性质时,需要建立薄膜的结构模型(通常为多层膜结构)并结合各层材料的色散关系进行数据拟合,从而获得材料的光学常数。图13是目前典型的椭偏分析流程,包括了测量、建模与拟合过程[68]。

图13 椭偏分析材料光学性质的基本流程[68] Fig.13 Basic flow chart of the optical properties of materials analyzed by ellipsometric analysis method[68]
椭偏测量是一种间接的测量技术,在分析椭偏参数时,要根据所测薄膜样品的实际结构和材料的光学色散关系建立合理的模型,并利用该模型对椭偏参数进行拟合。由此可见,建立的模型与薄膜实际结构的匹配程度决定了数据拟合的准确性。通常模型的选择并不是唯一的,为了判定拟合数据的准确度,常用的方法是利用模型中的各项参数计算出ψ和Δ的理论值,再通过比较计算理论值与测量结果间的误差进行修正,即进行回归分析,这就是上图所示的椭偏拟合步骤。最后得到的最优分析结果即为该模型下椭偏拟合的结果。计算量很大,通常需要借助计算机辅助计算才能顺利完成。
在椭偏拟合的过程中,采用均方误差(Mean Squared Error,MSE)来描述拟合值相对测量值的偏离程度,其表达式如下[69]:
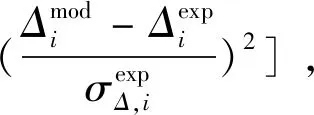
(16)
其中,σ为测量误差,N为测量中得到的椭偏参数ψ(或Δ)个数,M为拟合模型中的变量个数。上角标“mod”和“exp”分别表示利用拟合模型求出的理论值与利用椭偏仪测得的测量值。MSE的值越小,椭偏拟合与测量结果越接近。当MSE值达到全局最小时,则认为拟合得到了材料的实际厚度与光学常数。
实际应用中,在最后获得薄膜厚度及光学常数后,常常还需要判断数据是否符合基本物理规律。对于光学常数正确性的判定方法是判断数据是否符合Kramers-Kronig关系(简称K-K关系),K-K关系表达式如下[69]:
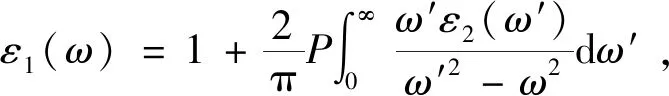
(17)

(18)
上式中,
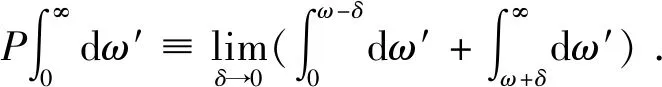
(19)
复折射率的实部n和虚部k也满足式(17)~(19)的关系。
5.2.2 逐点(point-by-point)椭偏参数反演
椭偏分析常常需要对待测材料建立模型并选用合适的光学色散模型进行拟合,但有些时候待测材料的光学色散模型并不容易建立,可能因为对于材料的光学性质未知,所以无法选择合适的色散模型;也可能是由于该材料的色散模型参数拟合过于复杂而无法完成。此时常常采用数学反演(mathematical inversion)的方法,就可以获取椭偏测量的光谱范围内待测材料的光学常数,其流程如图14所示。
从流程图可以看出,使用逐点椭偏参数反演方法进行拟合时与传统椭偏分析开始时步骤相同,首先都要为待测材料建立一个合理的光学模型。根据式(8)知道椭偏参数是入射角θi、入射光波长λ、每层膜厚di和复折射率i的函数,假定所关心的是第一层膜的光学常数1,所以在已知其他层厚度和光学常数时,椭偏参数(ψ,Δ)就是入射角θi、入射光波长λ和第一层膜的光学常数1的函数。所以首先使用色散模型拟合出第一层膜厚的数值d1,然后使用点对点数据反演和第一步拟合出的膜厚数据就可以求解出第一层膜的复折射率的实部n1和虚部k1。

图14 逐点椭偏参数反演方法分析椭偏参数的基本流程[70] Fig.14Basic flow chart of ellipsometric parameters analyzed by point-by-point ellipsometric parameter inversion method[70]
由此可见,逐点椭偏参数反演方法实际上是在每一个椭偏参数测量点处使用数学反演求解出该点波长对应的光学常数,于是也被称为点对点拟合方法(Point-by-point method)。此方法与使用色散模型进行椭偏分析的基本不同点在于,点对点拟合在不同波长求解光学常数时是相互独立的。值得注意的是:点对点拟合第一步使用色散模型拟合的膜厚结果,决定了第二步数学反演结果的准确性。换句话说,第一步光学模型和膜厚的偏差都会导致最后求解的光学常数出现错误[71]。通常为了检验光学常数正确性有两种方法:一方面看吸收边和特征结果是否符合实际;另一方面判断该结果是否符合K-K关系。
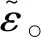
2016年,复旦大学的J.P.Xu(许骥平)等人使用逐点椭偏参数反演的方法研究了ZrO2超薄膜光学带隙及电子缺陷的厚度依赖特性[72]。他首先使用透射电子显微镜(Transmission Electron Microscope,TEM)和原子力显微镜(Atomic Force Microscope,AFM)对原子层沉积(Atomic Layer Deposition,ALD)方法制备的ZrO2超薄膜进行了表征,发现ZrO2超薄膜表面存在粗糙层,并且和衬底之间存在界面层。考虑到界面层的光学常数较难获取,故建立了Si衬底/等效ZrO2/大气的三相光学模型(如图15(a)、15(b)所示)来分析样品的椭偏响应。其中,等效ZrO2层代表了来自界面层和ZrO2膜的共有贡献。建立光学模型后,使用柯西色散模型对透明区内的椭偏光谱进行拟合,获取了各样品的厚度。此时三相光学模型下的椭偏参数(ψ,Δ)仅是等效层光学常数(ε1和ε2)的函数,使用点对点方法从中解出每个波长下的ε1和ε2,其中ε2结果如图15(c)所示。
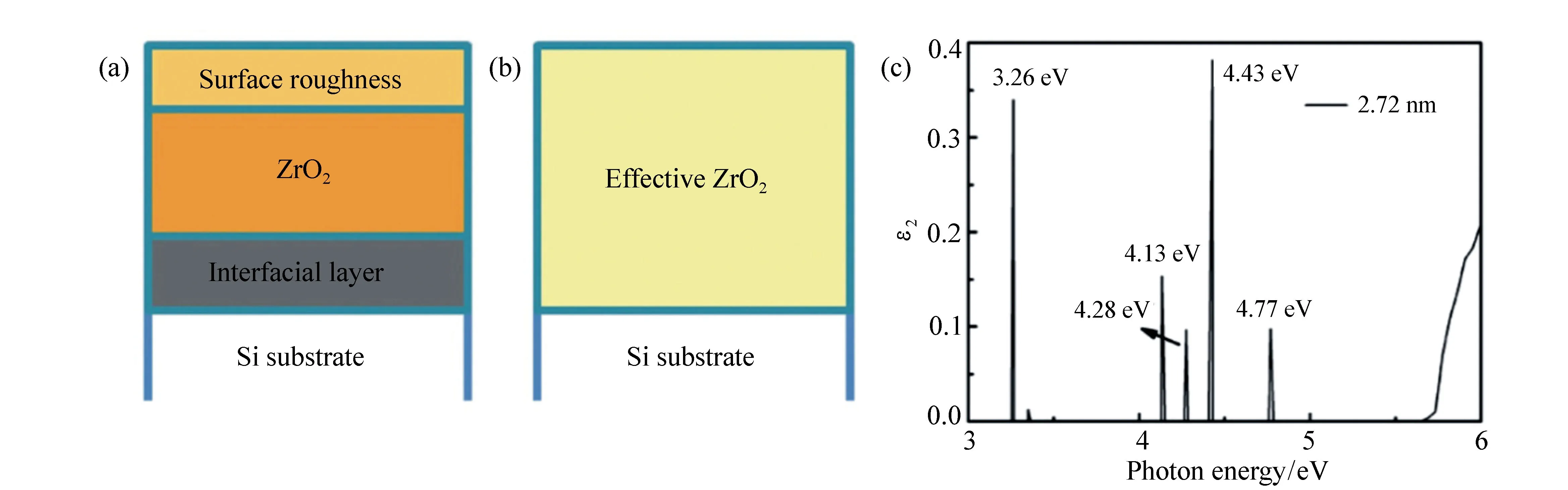
图15 逐点椭偏参数反演方法分析ZrO2超薄膜。(a)ZrO2超薄膜的光学模型,(b)点对点分析中使用的简化光学模型,(c)厚度为2.72 nm的ZrO2超薄膜在入射光子能量为3~6 eV内的ε2[72] Fig.15 Analysis results of ultrathin ZrO2 films by point-by-point method. (a)Optical model of ZrO2 samples, (b)simplified one for point-by-point analysis in this work, (c)imaginary model of dielectric constants of the effective ZrO2 film with a thickness of 2.72 nm when incident photon energy is 3~6 eV range[72]
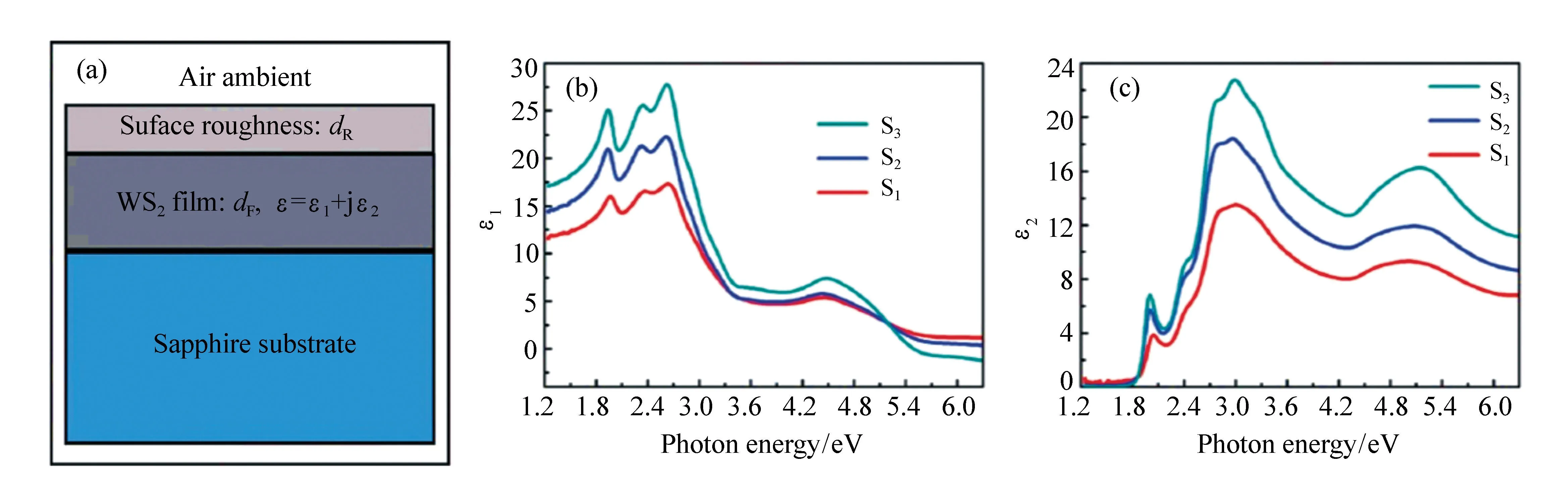
图16 逐点椭偏参数反演方法分析WS2超薄膜。(a)WS2超薄膜的光学模型,(b)和(c)分别是点对点拟合得到的WS2超薄膜复介电函数实部ε1和虚部ε2(入射光子能量范围为1.2~6.3 eV,S1、S2和S3分别代表溅射时间为20、50和70 s的3种样品)[73] Fig.16 Analysis results of ultrathin WS2 films by point-by-point method. (a)Optical model of WS2 samples, (b) and (c) are real part ε1 and imaginary part ε2 for dielectric function extracted from point-by-point fitting respectively. (the photon energy range is 1.2~6.3 eV,S1,S2 and S3 are represeroted the sample for the sputtering times, 20 s, 50 s, and 70 s, respectively)[73]
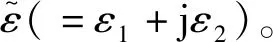
6 椭偏光谱分析模型及其应用
椭偏分析是一种基于模型的拟合方法,而在模型中的各种材料需要用其对应的色散关系来描述。材料的色散关系是指材料的光学常数是光波长或频率的函数,当光的波长改变时,其复介电函数通常也会发生变化。因此,在建立椭偏分析模型时,根据待测材料的性质为其选择合适的色散模型是十分重要的一步。材料的色散关系可以由物理模型推导而得到。本文接下来将简要介绍一些常用的光学色散模型。
6.1 光学色散模型及其应用
在20世纪初期,P.Drude[74]和H.A.Lorentz[75]等人分别对金属和电介质的光学经典理论作出了贡献,这些经典模型说明了金属和电介质的光学性质和光谱的一些基本特点[75]。其他许多光学色散模型都是基于这两个经典模型的理论演变得到的。
6.1.1 洛伦兹(Lorentz)色散模型
Lorentz模型是描述介质材料最重要的经典模型之一[34,75]。一些常见的色散模型,如Tauc-lorentz模型[76]、Sellmeier模型[34]、Cody-lorentz模型[77],都是由Lorentz模型变化而来的。
Lorentz模型将物质视为许多振子的线性组合,这些振子在光场的电磁辐射作用之下在其平衡位置附近做受迫振动。实际上,振子概念要更普遍,可以是电子、原子或原子团等[34]。物理上,此模型可以看作核外电子受原子核的束缚,在其平衡位置做受迫振动,由于原子核的质量远大于电子,因此原子核的位置即为平衡位置。图17为束缚电子的受力分析示意图,从图中可以看到,束缚电子受到回复力、阻尼力和电磁辐射电场的作用力3种力的作用。

图17 束缚电子的受力分析示意图[34] Fig.17 Force analysis diagram of bound electron[34]
根据牛顿第二定律可写出束缚电子的运动方程如下:
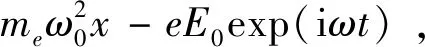
(20)
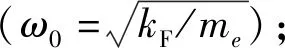
x(t)=aexp(iωt) ,
(21)
将式(21)代入式(20)可得:
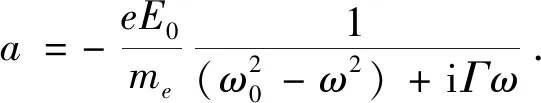
(22)
设电子密度为Ne,则电介质极化率χ=-eNex(t)/E0exp(iωt),可以得到复介电函数ε=ε0s+χ为:

(23)
其中,ε0s为频率远大于测试频率范围的复介电函数实部对复介电函数的贡献,常取ε0s=1。并且在实际数据处理中,通常采用光子能量En来描述洛伦兹模型,即:
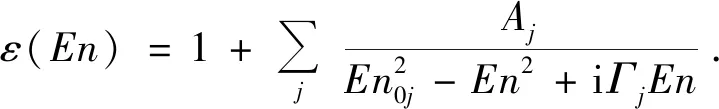
(24)
由于材料中振子对应的共振能量(带隙)往往有多个,因此要用如式(24)所示的振子叠加形式表示。Aj表示第j个振子的振动强度,单位是eV2;Γj为第j个振子的阻尼系数,单位是eV;En0j为第j个振子对应的带隙能量,单位是eV。
Lorentz模型常用于描述半导体、绝缘体和晶体材料等受限电子系统。也可用于纳米尺度金属颗粒组成的薄膜;金属粒子嵌入绝缘体矩阵的综合体材料[34]。
首先介绍几例Lorentz模型最简单的应用:2016年,复旦大学的D.D.Zhao和Q.Y.Cai等人分析了电子束蒸发退火制备的不同厚度五氧化二铌(Nb2O5)薄膜的光学常数[78]。椭偏参数拟合时,首先根据制备样品的结构建立了对应的三相光学模型:硅衬底/Nb2O5/Air,再利用Lorentz单振子色散模型拟合得到Nb2O5薄膜的光学常数。同样在2015年,Lancaster University的M.Esro和G.Vourlias等人在分析氧化铪(HfO2)薄膜的光学常数时也选用的是Lorentz单振子色散模型[79]。由此可以看出,Lorentz单振子模型符合材料的电子结构,并且主要对应于材料中高能态带到带跃迁的贡献。
由于材料中振子对应的共振能量(带隙)往往有多个,Lorentz模型在应用时常常使用如式(24)所示的多振子叠加形式。例如:2000年,瑞典Linköping University的R.Jansson和S.Zangooie等人在使用椭偏光谱法分析3C-SiC的光学性质时,首先建立了四相光学模型:Si(100)衬底/3C-SiC(100)层/SiO2层/环境,描述3C-SiC(100)层光学性质时使用了多振子叠加形式的Lorentz模型[80]。
多层膜结构中的界面层有时也可以使用Lorentz模型描述。2012年,复旦大学的D.X.Zhang(张冬旭)等人在研究Ta2O5超薄膜光学性质与膜厚的关系时,使用椭偏光谱分析技术测试了沉积在硅衬底上的Ta2O5超薄膜[81]。椭偏拟合时,考虑了氧化物薄膜与硅衬底之间可能存在的硅诱导间隙态(silicon-induced gap states,SIGS),于是建立了四相光学模型:硅衬底/SIGS界面层/Ta2O5超薄膜/环境,随后使用Lorentz单振子模型描述了SIGS界面层的光学性质。2014年,D.X.Zhang(张冬旭)等人在使用椭偏技术研究锡薄膜从固态变化到液态过程中光学性质的改变时,考虑在加热过程中,通过X射线衍射光谱(X-ray diffraction spectroscopy,XRD)表征结果可知锡薄膜加热至熔点及更高温度后会发生氧化,并且产生了含有液体锡、氧化锡和氧化硅的混合物夹层[82]。据此建立五相光学模型:硅衬底/Sn薄膜/混合物夹层/SiO2封层/大气环境,其中混合物夹层的光学性质使用Lorentz多振子模型描述。
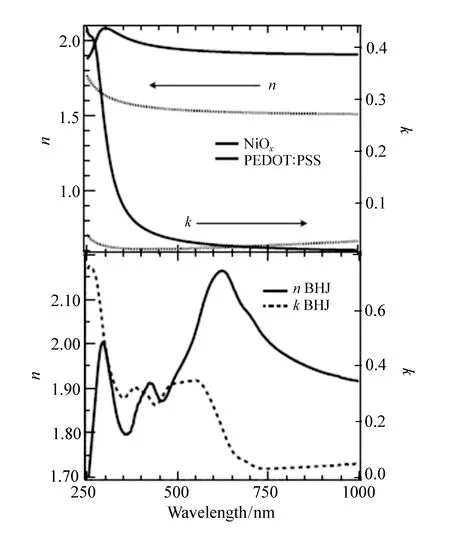
图18 NiOx, PEDOT∶PSS和体异质结(BHJ)太阳能电池的复折射率[83] Fig.18 Index of refraction, n and extinction coefficient, k for NiOx , PEDOT∶PSS and BHJ solar cells[83]
Lorentz模型在太阳能材料的分析中也有应用。2011年,University of Arizona的K.X.Steirer和P.F.Ndione等人在分析NiOx,PEDOT∶PSS和体异质结(BHJ)太阳能电池的复折射率时也使用的是Lorentz模型[83],拟合出的复折射率如图18所示。
2015年,Indian Institute of Technology Madras的M.Ghosh和L.Pradipkanti等人使用椭偏技术分析了层间束缚了水层的氧化石墨烯[84]。为了分析水层对氧化石墨烯(graphene oxide,GO)光学性质的影响,他们将样品在不同温度下进行退火处理。结合XRD测试结果,研究人员分析得到退火温度在180 ℃以上时GO中束缚的水层可以被完全除去,此时GO薄膜可以认为是由均匀的分层GO薄片组成的,再结合GO在可见光区域具有显著吸收的性质,于是使用Lorentz三振子模型对GO薄膜进行椭偏拟合。而退火温度低于180 ℃时,由于束缚水层的存在,GO薄膜和束缚水层此混合体系的椭偏拟合将使用后文中介绍的有效介质近似模型(EMA)描述。其中GO介质的光学性质仍使用Lorentz三振子模型进行拟合,但是由于退火温度的不同,此时模型中振子的中心能量将由较高退火温度下测得的中心能量再结合振子的振幅和能量扩展趋势线性外推获得。振子中心能量线性拓展和λ=600 nm不同退火温度本征GO薄膜和束缚水的GO综合体系的光学常数曲线如图19所示[84]。
图19 GO薄膜的椭偏光谱分析。(a)Lorentz模型3个振子中心能量按退火温度线性拓展(C1(方块),C2(圆圈),C3(三角));(b)λ=600 nm时不同退火温度下本征GO薄膜和束缚水的GO综合体系的光学常数曲线(本征GO薄膜的nGO(1),kGO(3),混合体系n(2),k(4),阴影部分为除去束缚水层的温度区间)[84] Fig.19 Ellipsometric spectral analysis of GO thin films. (a)Three vibrator center energies of Lorentz model linearly expand according to annealing temperature (C1(squares), C2(circles), and C3(triangles)), (b)optical constant curve of GO synthesis system of intrinsic GO film and bound water nGO(1), kGO(3), and total n(2), k(4) vs. Tann for λ=600 nm. Dashed region denotes temperature interval where water is expelled[84]
6.1.2 塞米尔(Sellmeier)模型
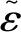
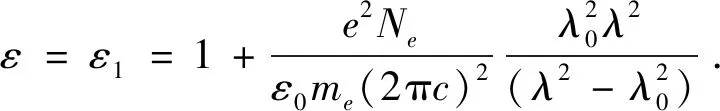
(25)
注意到,当Γ=0时,有ε2=k=0,因此通过重写上式Sellmeier模型可以表示为:
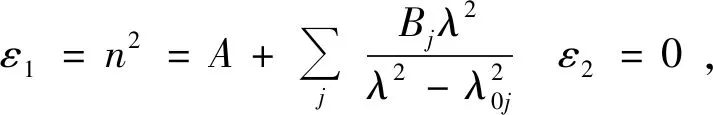
(26)
其中,λ0与ω0相对应,A和Bj为椭偏拟合中的可变量。
Sellmeier模型适用于描述透明材料(无吸收ε2=k=0),如:SiO2、MgF2、TiO2和BK7玻璃等;或者用于描述透明介质材料,如在红外光谱区描述Ge、Si和GaAs(砷化镓)等。
2014年,复旦大学的D.X.Zhang(张冬旭)等人使用椭偏技术研究锡薄膜从固态变化到液态过程中光学性质的改变[82],椭偏测试光子能量范围
为:1.5~4.5 eV。椭偏参数拟合时,首先建立五相光学模型:硅衬底/Sn薄膜/混合物夹层/SiO2封层/大气环境,紧接着考虑到SiO2封层在测试波段透明,于是用Sellmeier模型描述其光学性质。2016年,复旦大学的L.Yang(杨辽)等人使用椭偏分析拓扑铋薄膜光学性质随温度的变化[85]。椭偏参数拟合时,根据样品的结构建立了四层光学模型:硅衬底/Bi薄膜/SiO2层/大气,同样因为SiO2层的吸收很小基本可以忽略为透明介质材料,所以使用Sellmeier模型描述。
2012年,D.X.Zhang(张冬旭)等人为研究Ta2O5超薄膜光学性质与膜厚的关系,使用椭偏光谱分析技术测试了沉积在硅衬底上的Ta2O5超薄膜[81]。考虑界面层,建立的光学模型为:硅衬底/SIGS(silicon-induced gap states)界面层/Ta2O5超薄膜/环境。其中,椭偏测试的波段为300~820 nm,由于Ta2O5在此光谱范围内是透明介电材料,所以使用Sellmeier模型描述拟合的结果如图20所示。
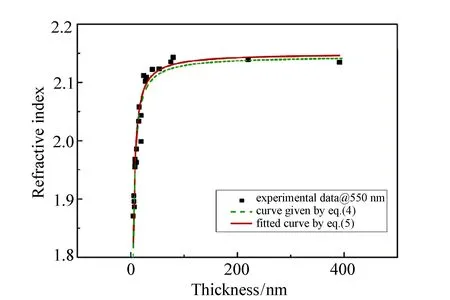
图20 550 nm处沉积在Si衬底的Ta2O5薄膜折射率实验值和理论值随薄膜厚度的变化[81] Fig.20 Experimental and theoretical refractive indices at 550 nm for the Ta2O5 films deposited on Si vary with thickness[81]
6.1.3 柯西(Cauchy)模型
Cauchy模型是一个由A.L.Cauchy提出的经验模型[34],通常用于描述材料在透明波段的色散关系。对式(25)进行级数展开,可以得到Cauchy模型的数学形式:

(27)
因此,Cauchy模型也可以看作是Sellmeier模型的数学近似,是一个经验模型。但是Cauchy模型也可应用于材料消光系数k不为零的情况,材料消光系数k表达式为:
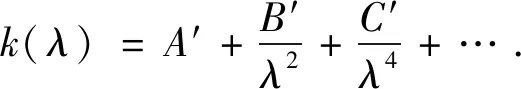
(28)
由Cauchy模型衍生出的柯西指数(Cauchy exponential)模型,其复折射率实部n(λ)部分保持不变,但是复折射率虚部消光系数k(λ)与波长呈指数关系,更符合材料的实际色散关系,并且使得柯西指数模型可以模拟的范围扩大。该模型中材料的光学常数表示为:
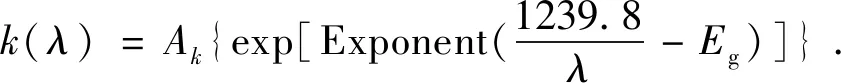
(29)
Cauchy模型适用于拟合透明或吸收较小的材料,如:Al2O3、SiO2、MgF2、TiO2和BK7玻璃等。2015年,复旦大学的Z.Y.Wang(王子仪)等人使用椭偏技术研究氧化铝(Al2O3)薄膜光学性质随退火温度和膜厚的变化时[86],建立了五相光学模型:Si衬底/ SiO2层/ Al2O3薄膜/表面粗糙层/大气,考虑到Al2O3薄膜在可见光区是透明的,所以使用Cauchy模型描述其光学性质。2017年,深圳大学的李彤等人将椭偏技术应用于键合型掺铒纳米晶-聚合物波导放大器的制备过程中[87]。他们使用椭偏技术测量分析了键合型掺铒氟钇钠纳米晶-聚合物(OA-NaYF4∶Er-PMMA)薄膜的光学性质,采用Cauchy色散模型拟合出该薄膜折射率随波长的变化。
除了一般的薄膜材料,Cauchy模型还可以应用于某些生物材料。例如,2011年浙江大学的J.Jiang和L.Zhu等人在研究沉积在疏水性聚合物膜上的自聚合多巴胺(pDA)涂层的表面特征时[88],使用椭偏技术分别测量了悬涂在硅衬底上的PVDF膜、沉积在PVDF上的pDA层和直接沉积在硅衬底上的pDA层厚度。为了使用椭偏参数拟合出pDA层厚度,使用Cauchy色散模型描述其光学性质。其中使用的Cauchy色散模型拟合参数为An=1.45,Bn=0.01。
Cauchy模型在二维材料中也有应用。2010年,曼彻斯特大学的V.G.Kravets和A.N.Grigorenko等人在使用椭偏技术分析石墨材料和石墨烯薄片时[66],首先直接使用Fresnel模型拟合了~1 μm厚的石墨复折射率,但是发现此方法拟合x向和z向的光学常数曲线存在一定的耦合,并且曲线也不太平滑(详细见图12)。为了减小曲线之间的耦合,研究人员重新使用Cauchy模型拟合了石墨材料z向的椭偏参数,结果如图21所示。与图12直接使用Fresnel公式拟合结果相比,使用Cauchy色散模型拟合得到的曲线更加平滑,并且有效地削弱了x向和z向光学常数曲线的耦合。第二部分研究内容是分析石墨烯薄片的光学性质,研究人员在椭偏拟合时建立了四相的光学模型:硅衬底/氧化硅层/Cauchy亚层(Cauchy sublayer)/石墨烯层,接着使用Cauchy色散模型拟合Cauchy亚层和石墨烯材料z方向的椭偏参数。其中Cauchy亚层代表石墨烯层与衬底之间的间隙层,一般认为是水和空气,其典型的Cauchy参数值为:膜厚d为2~4 nm,A≈1.03,B≈ 0.08,C≈-4×10-4。石墨烯层的厚度为0.335 nm,最终获得的光学常数x向分量拟合结果如图22所示(z向拟合结果类似于石墨)。
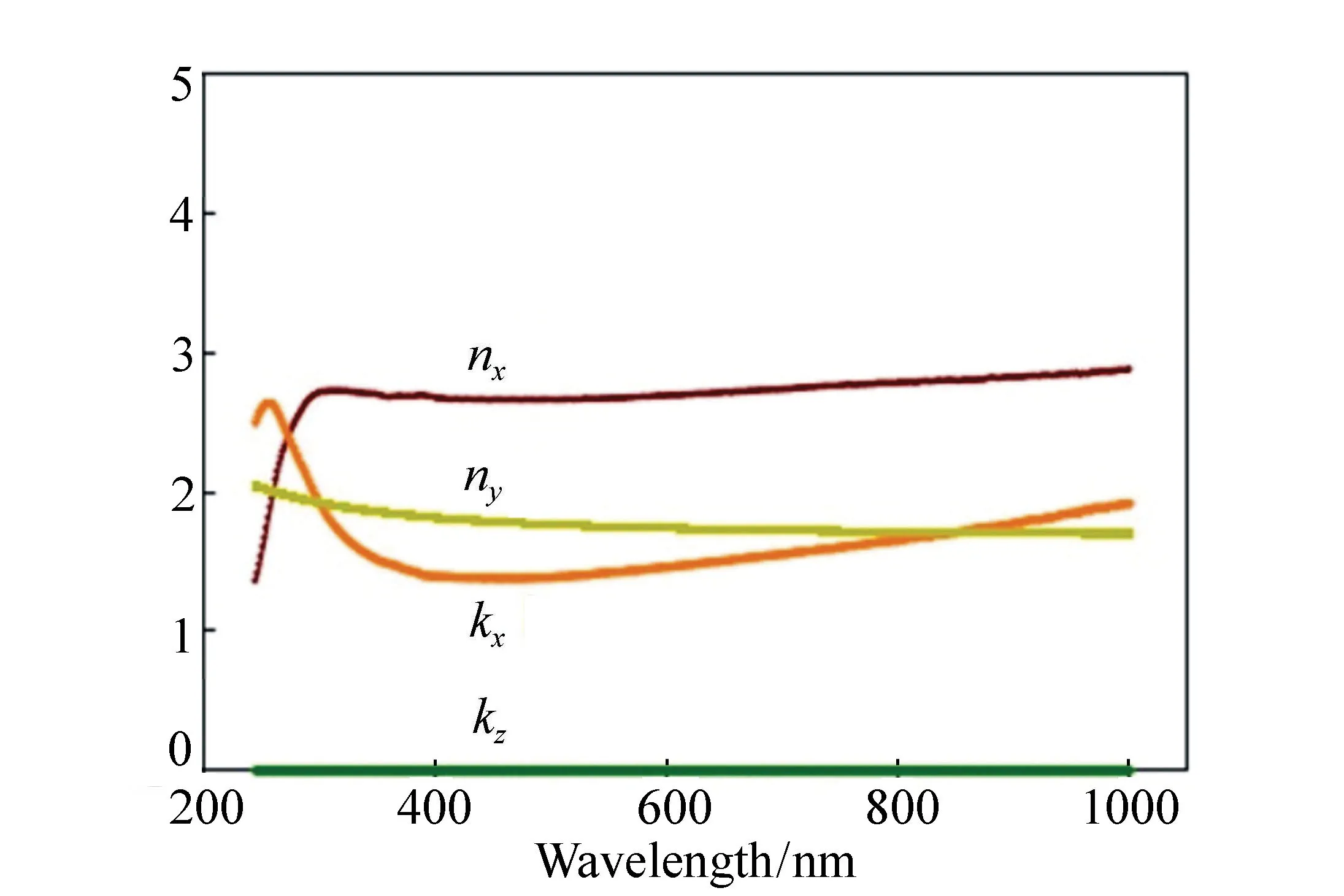
图21 椭偏光谱分析得到的~1μm厚石墨x向和z向的复折射率(此时z向被认为是Cauchy材料)[66] Fig.21 Complex refractive indexes in the x- and z-directions of ~1 μm thick graphite obtained by ellipsometry(optical constants of graphite with z-component being treated as a Cauchy material)[66]
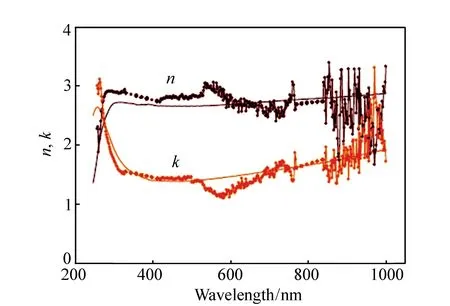
图22 采用多角度椭圆偏振光谱法分析制备在硅衬底上的石墨烯薄片的光学常数(x向)[66] Fig.22 Reconstructed x-component optical constants of graphene prepared on silicon substrate using multi-angle spectroscopic ellipsometry[66]
6.1.4 F-B(Forouhi-Bloomer)模型
F-B模型是由A.R.Forouhi和I.I.Bloomer在1986年提出的适用于半导体和介质的光学色散模型[89-90]。该模型从激发态且寿命有限的单电子推导出消光系数k的表达式,再利用Kramers-Kronig关系得到复折射率的表达式[91]。F-B模型的n、k表达式为:
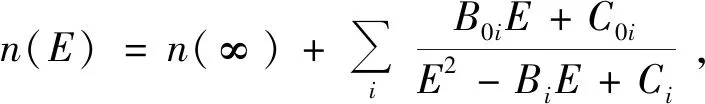
(30)
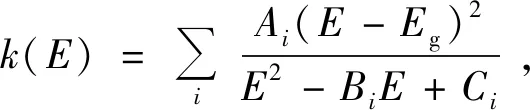
(31)
其中:
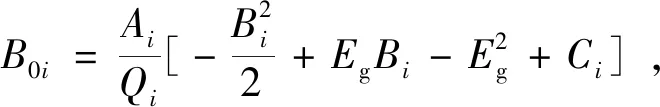
(32)
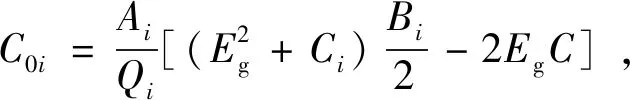
(33)
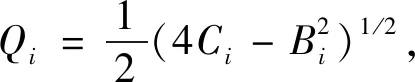
(34)
n(∞)为入射光能量E趋于无穷大时材料的折射率,与经典色散模型不同,在E→∞,k(E)→0时,F-B模型认为n(∞)=1+ca,c为光速,a为正常数,则可以得到n(∞)>1。式中,i代表多项式的项数;Eg为材料的光学带隙;A为权重因子,代表跃迁几率,与激发态寿命成反比;B/2决定了k(E)谱的横坐标位置;C略大于(B/2)2,与B共同决定峰值高度。同时,B0i、C0i和Qi并不是相互独立的系数,而是由Ai、Bi、Ci、n(∞)和Eg共同决定的。
F-B模型常被用来描述半导体(禁带宽度附近)和介质材料的光学性质。并且F-B模型中常常需要价带和导带态密度与能量的关系往往是抛物线型[92]。对于无定形半导体材料,k谱较为平缓,常为单峰结构,i=1即可较好地描述其色散关系[93]。对于晶体材料,k峰较为尖锐且常为多峰或带有若干肩的单峰结构,需要用多项拟合[94]。在描述非晶态材料的光学性质时,要求该材料在光谱区的光学性质主要有价带和导带的带间跃迁决定。
2017年,复旦大学的Y.J.Shi(石跃杰)等人使用椭圆偏振光谱分析技术研究了使用ALD制备的厚度小于20 nm TiO2超薄膜的光学性质和带隙性质随材料相变的演变[95]。厚度小于20 nm TiO2超薄膜通过ALD技术生长在Si(100)衬底上。椭偏测试的波段为200~1 000 nm。根据AFM和TEM的表征结果可知,制备薄膜表面粗糙层的厚度较小,所以在之后数据分析时建立的光学模型(四相模型:Si衬底/Tix-SiyO2界面层/TiO2/air)中不含该层。椭偏参数拟合时,考虑到F-B模型可以较为准确地对无序介质中吸收阈值附近的激励作出适当的描述,所以使用F-B模型拟合TiO2超薄膜的光学性质。拟合得到的结果如图23所示。
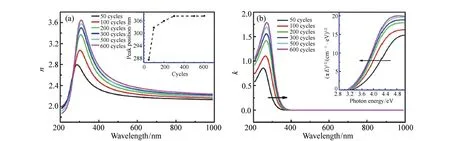
图23 400 ℃退火后不同厚度的TiO2超薄膜复折射率谱。(a)折射率n,(b)消光系数k。(图(a)的插图显示了峰位置与ALD循环数的关系,图(b)的插图显示了在400 ℃下退火后不同厚度的TiO2超薄膜的(αE)1/2vs.E图)[95] Fig.23 Complex refractive index spectra for TiO2 ultrathin films with different thicknesses after annealing at 400 ℃. (a)Refractive index n spectra, (b)extinction coefficient k spectra.(The insert of (a) shows plot of peak position versus ALD cycles. The insert of (b) shows plots of (αE)1/2vs. E for TiO2 ultrathin films with different thicknesses after annealing at 400 ℃)[95]
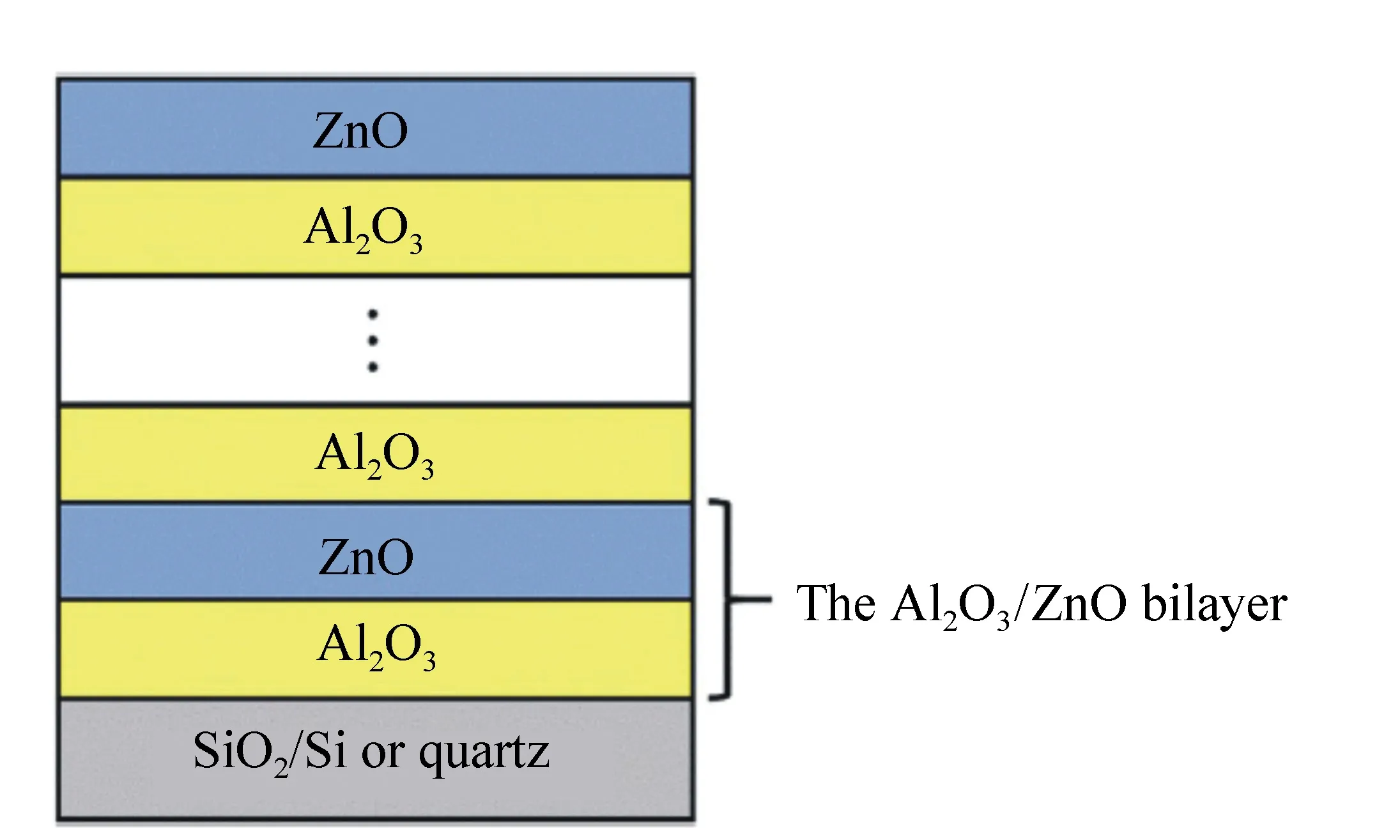
图24 Al2O3/ZnO纳米层状结构示意图[96] Fig.24 Structure diagram of the Al2O3/ZnO nanolaminates[96]
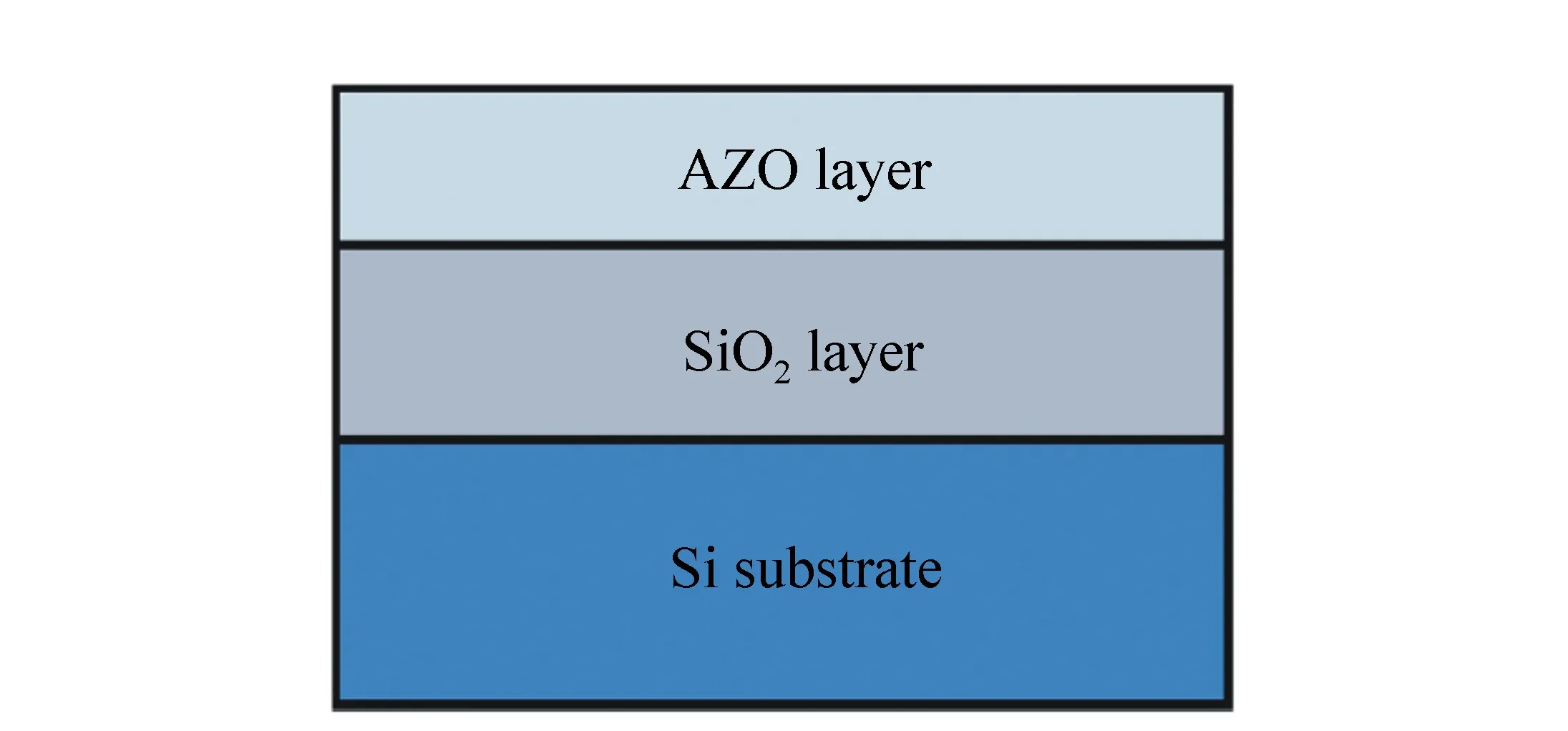
图25 用于椭偏分析多层膜样品的光学模型[96] Fig.25 Optical model of samples for SE analysis[96]
F-B模型还可用于拟合多层纳米复合膜的光学性质。2017年,复旦大学的D.H.Li(李大海)等使用椭偏技术研究了Al2O3/ZnO多层膜系统[96]。将Al2O3/ZnO双层膜结构作为一个单元,循环多个周期堆叠成如图24所示的多层膜系统,并且单元中单层Al2O3和单层ZnO薄膜厚度总是相等的,研究的目的是分析不同Al2O3/ZnO单元层厚度对纳米层状结构多层膜系统的形貌,光学和电学性质的影响。椭偏参数拟合时,第一步是建立光学模型,根据研究样品的性质,李大海等人建立了如图25所示的三层膜结构,分别为:硅衬底/SiO2层/AZO(Al2O3/ZnO多层膜系统)。第二步使用色散模型拟合椭偏参数时,使用F-B模型拟合AZO层的光学常数和厚度。拟合得到的膜厚与TEM测试的结果相符,说明光学模型和色散模型选择都比较恰当。拟合的AZO层复折射率如图26所示。
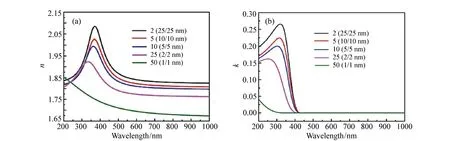
图26 生长在SiO2/Si衬底上的纳米层状结构多层膜系统的光学常数。(a)折射率n;(b)消光系数k[96] Fig.26 Optical constants of nanolaminates grown on SiO2/Si substrate. (a)Refractive index n; (b)extinction coefficient k[96]
近几年来,对于太阳能材料的研究开展地如火如荼。其中最典型的一种材料就是钙钛矿薄膜(CH3NH3PbI3,Perovskite Thin Films)。考虑到其纳米晶体的性质,常常使用F-B模型和Jobin Yvon参数化后的F-B模型拟合其光学性质[97]。2014年,瑞士University of Ljubljana的P.Löper和M.Stuckelberger等人使用椭偏技术分析了CH3NH3PbI3钙钛矿薄膜的复折射率光谱[98],首先建立四相光学模型:玻璃衬底/CH3NH3PbI3钙钛矿薄膜/表面粗糙层/大气环境,如图27(a)所示。之后使用Jobin Yvon参数化后的F-B模型拟合了CH3NH3PbI3钙钛矿薄膜的复折射率光谱,拟合结果如图27(b)所示。
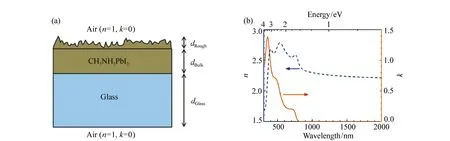
图27 CH3NH3PbI3钙钛矿薄膜椭偏分析。(a)作为光学模型的样品结构,(b)复折射率光谱[98] Fig.27 SE analysis of CH3NH3PbI3 perovskite thin films. (a)Sample structure used for the optical model, (b)refractive index[98]
同年,北京大学的Z.Xie等人同样使用椭偏技术分析了CH3NH3PbI3钙钛矿薄膜的复折射率光谱[99]。不同的是,结合AFM表征结果,他们发现钙钛矿薄膜中常常存在不定量的孔隙,且越靠近表面薄膜越疏松,表面粗糙度很大。于是建立了如图28所示的光学模型。

图28 在石英衬底上CH3NH3PbI3膜的表面粗糙层三层膜结构光学模型的示意图[99] Fig.28 Schematic of the three-layer surface roughness model of the CH3NH3PbI3 film on a quartz substrate[99]
图28中,底层充满了CH3NH3PbI3材料,而中间层和最上层是具有不同百分比空隙的CH3NH3PbI3材料。各层结构的厚度和空隙占有率都是待拟合的参数(上图中标注的数据为拟合结果)。而CH3NH3PbI3钙钛矿薄膜材料光学常数的拟合同样使用的是Jobin Yvon参数化后的F-B模型,拟合结果如图29所示。

图29 计算得到CH3NH3PbI3材料的复折射率谱[99] Fig.29 n(λ) and k(λ) results of CH3NH3PbI3 material[99]
比较两研究团队对钙钛矿材料的复折射率拟合结果,可以发现两者建立的用于拟合的光学模型不同,最终拟合的结果在对应波段也略有不同。
引起这些差异的因素除了拟合时选用了不同的光学模型,也与制备样品的差异和选用了不同的衬底等因素有关。但是因为测试波段内钙钛矿材料的光学特性相同,所以两团队都使用了相同的色散模型进行拟合,说明拟合步骤中光学色散模型的选取需要依据材料在相应椭偏测试波段的性质。
6.1.5 Tauc-Lorentz模型
Tauc-Lorentz模型基于J.Tauc等人提出的半导体带边理论[76,100]。适用于描述非晶态材料或透明导电氧化物。使用Lorentz模型计算出材料复介电函数的虚部ε2是完全对称的,由于非晶态材料的ε2峰表现出不对称的形状,所以在Tauc-Lorentz模型中,ε2的建模是通过创造一个特殊的带隙(称Tauc带隙),同时结合Lorentz模型进行计算的[34]。
非晶态材料的Tauc带隙能量Eg使用下式计算:
ε2=ATauc(En-Eg)2/En2.
(35)
再将上式ε2表达式代回Lorentz经典表达式(式(24)),得到非晶态半导体材料复介电函数虚部的表达式如下:

(36)
式中A、C为拟合参数,分别表示Tauc-Lorentz振子的振幅和阻尼因子(C=Γ),En0为Tauc-Lorentz振子的中心能量,Eg为带隙能量,复介电函数的实部由Kramers-Kronig关系积分得到。相对于Lorentz振子模型,Tauc-Lorentz模型能够更好地描述半导体材料在带边附近的光学常数,并且可以解决F-B模型中能量在带隙下消光系数k不为零的问题,提出后获得了广泛的使用。
Tauc-Lorentz模型适用于拟合非晶态材料和透明导电氧化物类型的材料。上节中钙钛矿材料拟合使用的色散模型都是Jobin Yvon参数化后的F-B模型。但是根据发表的文献,钙钛矿材料在其他波段的椭偏拟合也可以使用Tauc-Lorentz模型。例如:2016年,复旦大学的Z.Y.Wang(王子仪)等人在使用椭偏技术研究水合物含量对一步法制备的CH3NH3PbI3钙钛矿薄膜性质的影响时[101],按照使用光学色散模型拟合椭偏参数的步骤,首先建立了光学模型:石英衬底/PEDOT∶PSS缓冲层/CH3NH3PbI3钙钛矿薄膜/表面粗糙层/大气环境。为了准确拟合PEDOT∶PSS缓冲层的光学常数,接下来使用椭偏技术单独测试了只覆盖缓冲层的石英衬底(石英衬底/PEDOT∶PSS缓冲层),拟合得到缓冲层光学常数。最后使用Tauc-Lorentz模型拟合了不同水合物含量的CH3NH3PbI3钙钛矿薄膜光学常数,如图30所示。

图30 不同水合物含量的CH3NH3PbI3薄膜复折射率谱。(a)复折射率实部n,(b)复折射率虚部k[101] Fig.30 Complex refractive index of CH3NH3PbI3 film with different levels of hydration water. (a)The refractive index n, (b)the extinction coefficient k[101]
之所以与之前介绍的研究小组使用了不同的色散模型,是因为两次使用的椭偏测试波段不同,更深层次的原因在于同种材料在不同波段的性质不同。Jobin Yvon参数化后的F-B模型适用于在可见或远紫外(FUV)区有吸收的非晶态材料(包括吸收电介质、半导体材料和聚合物等)。与Tauc-Lorentz模型相比,后者在实验材料的吸收区拟合的更好,前者适用于更宽波段的拟合[97]。瑞士卢布尔雅那大学和北京大学的研究团队椭偏测试的波段为300~2 000 nm,此波段是包含吸收波段在内的更宽范围,而复旦大学王子仪测试的波段为300~900 nm,更专注于吸收波段的椭偏参数拟合。2015年,日本岐阜大学(Gifu University)的Masaki Shirayama和Hideyuki Kadowaki等人在研究混合钙钛矿太阳能电池中的光学跃迁时使用了椭偏技术[102]。其中在测试混合钙钛矿太阳能电池中CH3NH3PbI3钙钛矿薄膜的光学性质时同样使用的是Tauc-Lorentz模型(入射光子能量范围为0.7~5.2 eV)。
Tauc-Lorentz色散模型还可应用于具有铁电性和反铁磁性材料光学性质的研究。2008年,J.F.Ihlefeld和N.J.Podraza等人使用椭偏技术分析了分子束外延生长(Molecular-beam epitaxy, MBE)的BiFeO3的光学带隙[103]。按照样品结构,研究人员建立了四相光学模型拟合椭偏参数,从下而上分别为:半无限厚SrTiO3衬底/ BiFeO3膜/表面粗糙层/大气环境。其中,BiFeO3膜的光学常数就使用Tauc-Lorentz四振子模型拟合得到。
Tauc-Lorentz色散模型在纳米晶体中也有应用。2017年,突尼斯Université de Gabès的F. Chaibi和R. Jemai等人在进行等离子体增强化学气相沉积法制备nc-Si∶H薄膜过程中氩和氦的稀释效应研究时[104],借助了椭偏技术测试了制备出薄膜的厚度。他们选用Tauc-Lorentz色散模型拟合了沉积在n型硅单晶衬底上的Si∶H薄膜的光学常数。
6.1.6 Drude模型[40]
Drude模型又称为自由电子气模型,适用于描述金属自由电子和半导体中自由载流子吸收使复介电函数发生变化的情况。当半导体中的自由电子以波矢K运动时,受到点缺陷的散射,散射后波矢变为K′,则自由载流子吸收就发生了。自由载流子吸收与点缺陷对自由载流子的散射如图31所示。
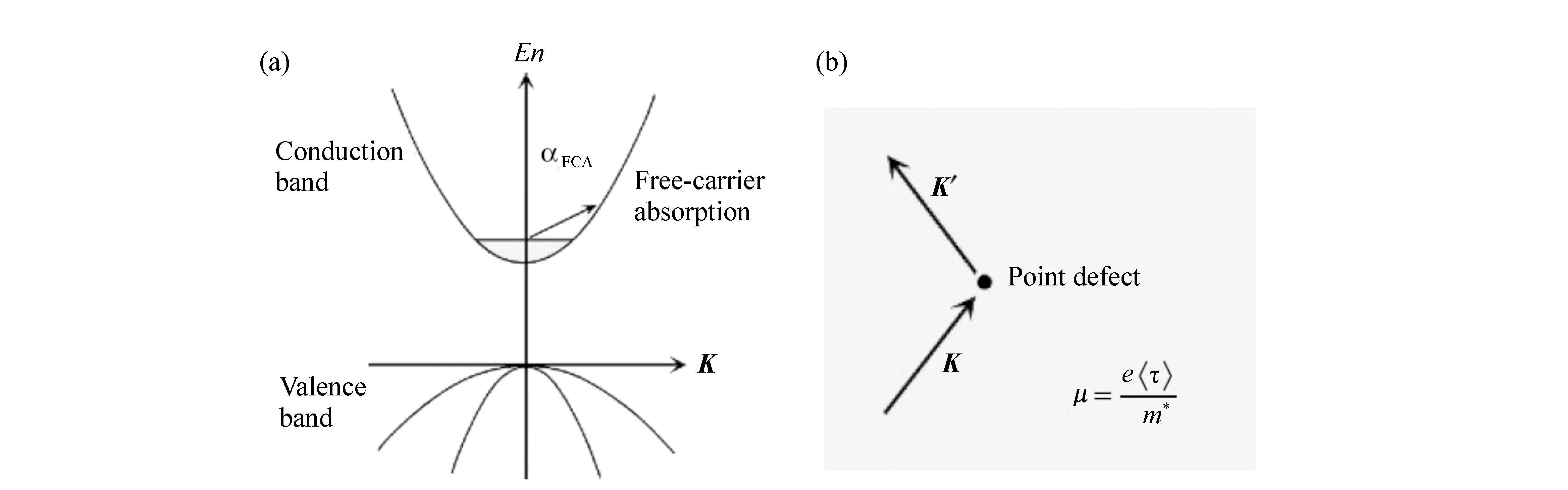
图31 半导体中自由载流子吸收示意图。(a)自由载流子吸收,(b)点缺陷对自由载流子的散射[34] Fig.31 Representation of free-carrier absorption in a semiconductor. (a)Free-carrier absorption,(b)scatter between free-carrier and point defect[34]
历史上,Drude模型先于Lorentz模型被提出[74-75],但Drude模型很容易由Lorentz模型推导出来。在Drude模型中,金属或者说导体中的电子被看作自由电子气,将带正电的原子核背景作为电荷补偿。自由电子不断地运动并从不同的速度方向受到散射,仍遵循牛顿定律。Drude认为这种运动与电流流过金属产生焦耳热的现象相同,他将散射归因于带电粒子之间的碰撞(例如,电子与带正电原子核)。实际上,这是因为固体偏离完全周期性,例如室温下的晶格振动[40]。按照这样的理论,自由电子不进行受迫振动,但仍受到正比于电子速度的阻尼力,此时式(20)等号右边第二项的回复力等于0,得到Drude模型的表达式[34]为:
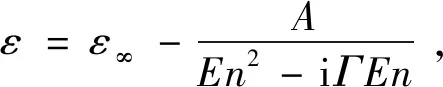
(37)
其中,
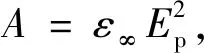
(38)
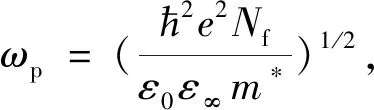
(39)
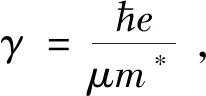
(40)
式中,Ep和γ表示等离子体能量和角频率的拓宽参数,ε∞为高频复介电函数,ωp为等离子频率,En为入射光子能量,ν为电子散射频率。
Drude模型是用于描述金属材料(如:Au、Ag和Cu等)或自由载流子浓度大的半导体。1983年,University of Missouri的M.A.Ordal和L.L.Long等人使用Drude模型拟合得到了包括铝、钴、铜、金、铁、铅在内的一共12种金属在红外和远红外波段的光学性质[105]。
使用Drude模型描述金属的光学性质时常常结合Lorentz模型,称作Drude-Lorentz(DL)模型。DL模型常用来描述红外频率区域的自由电子带内跃迁和可见/近紫外区域的束缚电子带间跃迁。该模型的表达式为[85,106]:
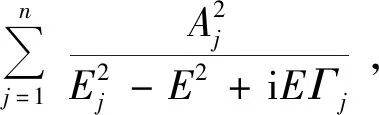
(41)
式中,ε、ε∞、Ep和Γp分别代表复介电函数、高频介电函数、等离子频率和Drude拓展。Aj、Ej和Γj分别表示第j个振子的强度、第j个振子的能量和第j个振子的阻尼。
2016年,南京邮电大学的E.T Hu(胡二涛)等人使用椭偏技术研究纳米金属薄膜厚度依赖的复介电函数[106]。由于所研究的金(Au)在可见/近紫外波段带间跃迁中具有非对称的跃迁线型,使用DL模型描述时会引入“人为”的(即不具有物理意义的)参数,所以胡二涛等使用Drude和临界点(Drude and critical points,即DCP)模型拟合可见/近紫外波段Au的带间跃迁[106-107]。DCP模型表达式如下[106]:

(42)
其中两个临界点分别对应于Au可见/近紫外波段的两个带间跃迁。与式(41)相比式(42)DCP模型引入φ参数表示带边效应。DCP模型满足K-K关系,但不满足“等离子总和规则”,所以只适用于有限的频率区间[107]。利用DCP模型拟合300~1 100 nm波段的纳米金薄膜的复介电函数,拟合时建立的四相光学模型包含:K9玻璃/Au层/表面粗糙层/空气,拟合的结果如图32所示。
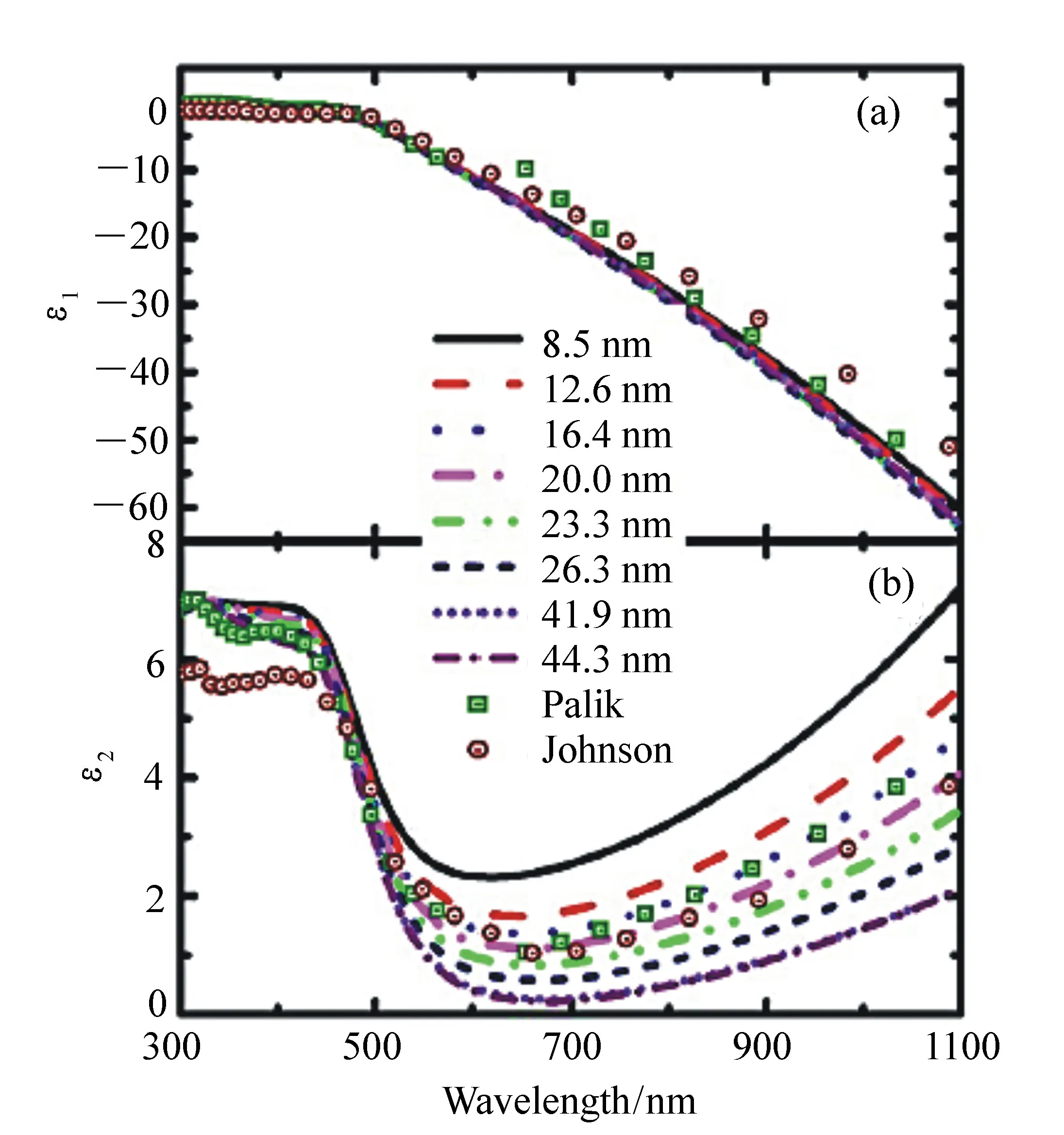
图32 不同厚度纳米金薄膜的复介电函数。(a)实部,(b)虚部[106] Fig.32 Dielectric functions of the nano-thin Au film with different thicknesses. (a)Real parts, (b)imaginary parts[106]
6.2 有效介质近似模型及其应用
前面介绍的几种色散关系都是针对单一均匀材料,但实际制备的材料往往是不均匀的。如薄膜材料,表面通常会有粗糙层;或者两种材料界面处产生的过渡层;或者某些情况下需要研究掺杂对于材料性质的影响等;也或者材料并不致密,中间存在孔隙等情况。而椭偏分析对于研究对象的表面和界面结构十分敏感,所以此时就需要考虑这些结构对材料光学性质的影响,就需要建立一种模型来正确描述多种材料复合后的介质所呈现的等效复介电函数。
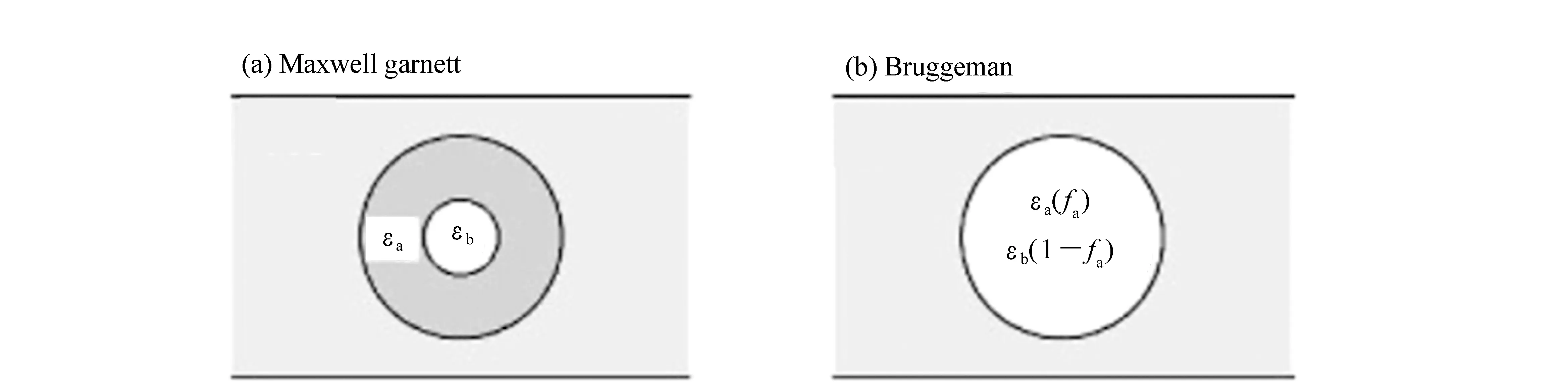
有效介质近似(Effective Medium Approximation,EMA)模型就是在这一背景下由D.Bruggeman首先提出的[108],该模型多用于描述多种复合介质的有效复介电函数,利用复合材料中各组分材料的含量及其原始复介电函数,就可以计算出复合材料的等效复介电函数,与此同时也可以获得复合材料中各组分的体积分数。EMA模型的一般表达式如下[108-109]:

(43)
其中,m为复合材料中包含的不同组分的数量,εj为第j种组分的复介电函数,fj为第j种组分的体积含量,〈ε〉为复合材料的等效复介电函数,εh为基质介质的复介电函数,γ是与退极化因子L有关的常数,随掺入材料的形状而改变:
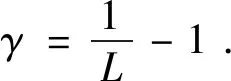
(44)
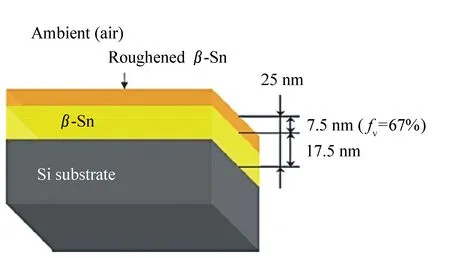
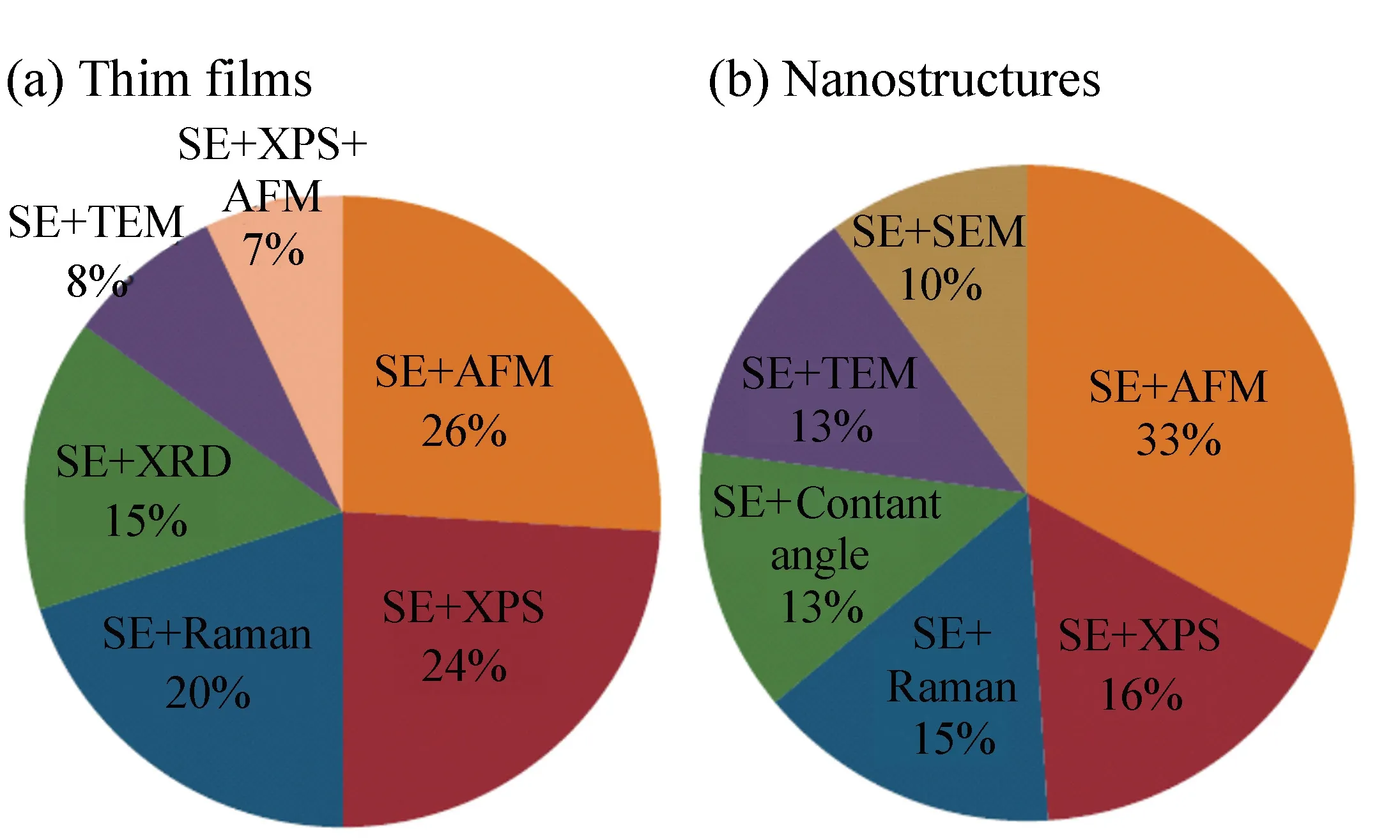
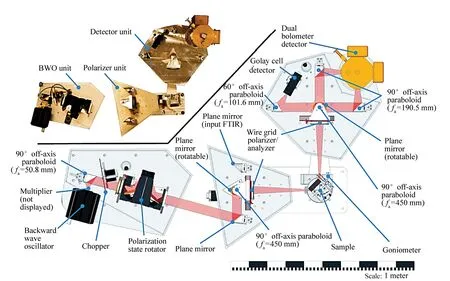
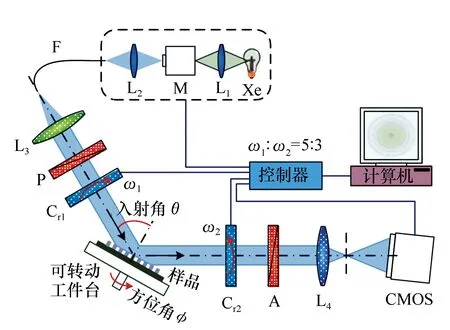
若复合材料中掺杂材料的形状是颗粒,则不同的L值代表不同的形状:当0 有效介质近似模型多用于描述含有多种组分的复杂材料,例如:不同介质分界面处的过渡层、材料表面的粗糙层、多孔材料(包括金属材料和空洞构成的金属薄膜)、掺杂材料、合金和多晶硅等。2017年,复旦大学的S.D.Yang(杨尚东)等人使用椭偏技术研究铋硒合金(Bi2Se3)的结构对其光学性质的影响(结构由纳米晶体变化到纳米薄片)[110]。为了拟合得到样品的光学常数,研究人员根据所制备样品的结构特征建立了四层光学模型:衬底/Bi2Se3薄膜/表面粗糙层/大气环境。其中,表面粗糙层视为Bi2Se3介质和大气的混合,其光学性质就使用EMA模型描述,并且没有对介质的体积分数进行人为规定,由拟合结果的RMSE(root-mean-square error)来确定拟合结果的准确性。 EMA模型不仅仅适用于拟合传统意义上由多种介质混合构成的复杂材料。同种材料由于处于不同的状态导致其光学性质存在差异,所以处于不同状态的同种材料构成的复合介质在光学研究中仍不能作为单一均匀材料处理,此时也可以使用EMA模型进行拟合。2004年,德国汉堡大学B.Schulz和D.Chan等人使用椭偏技术对指甲中角蛋白组织的水合和脱水过程进行研究[67]。研究人员将角蛋白组织中的水分为3种状态:自由水(复折射率为free)、结合水(复折射率为bound)、环境水。3种状态水之间的转化使用速率方程来表示,并且通过指甲光学常数的变化来描述水合和脱水的过程。较为新颖的是指甲光学常数的拟合过程中两次使用EMA模型。研究人员使用3种组分构成拟合时使用的光学模型:①基本基质材料;②结合了自由水的指甲组织;③结合水-角蛋白复合物。首先将③嵌入②的复杂材料作为中间介质,使用一次EMA模型,其中③的体积分数为:q=bound/(free+bound);第二步,再次使用EMA模型拟合由中间介质嵌入①构成的复杂体系的光学常数,其中中间介质的体积分数为:q=(free+bound)/(free+bound+1),最终的拟合结果如图33所示。 图33 指甲的光学常数和实验值(垂直虚线表示从水合作用到脱水作用的变化)[67] Fig.33 Optical constants and experimental values of finger nail.(The vertical dashed line marks the change from hydration to dehydration)[67] 根据基质材料的选择不同,EMA模型又分为3种:Lorentz-Lorentz模型、Maxwell-Garnett模型和Bruggeman模型。3种模型分别适用于不同种类的复合材料,其中含有两种组分的Maxwell-Garnett模型和Bruggeman模型的物理模型如图34所示。 图34 有效介质近似理论的物理模型。(a)Maxwell-Garnett模型;(b)Bruggeman模型[34] Fig.34 Physical models for effective medium theories. (a)Maxwell Garnett, (b)Bruggeman[34] 6.2.1 Lorentz-Lorentz模型 对于Lorentz-Lorentz模型,令εh=1,表示选择大气(空洞)为基质材料。Lorentz-Lorentz模型基于Clausius-Mossotti方程,是最早出现的EMA模型[40]。它假定各个组分是在原子尺度上的混合,因此在描述真实材料方面的应用存在限制,因为复合材料往往是在更大的尺度上的混合。Lorentz-Lorentz模型的表达式如下: (45) Lorentz-Lorentz模型通常用于描述孔隙型材料。 6.2.2 Maxwell-Garnett模型 Maxwell-Garnett模型中εh=εl,将最大占比的组分作为基质材料(其复介电函数为εl)。当掺杂物的比例显著小于主体材料的比例时,Maxwell-Garnett模型最实用。Maxwell-Garnett模型的表达式如下: (46) Maxwell-Garnett模型适用于具有非对称结构的复合材料,或者复合材料中只有少量组分掺杂的情况,并且掺杂组分镶嵌在基质材料中,被基质材料完全包围(如图34(a)所示)。最典型的是用于拟合远低于渗透阈值时,金属颗粒掺杂介质基体或纳米晶体嵌入其他基体形成的复合材料。 2009年,复旦大学的R.J.Zhang(张荣君)等人使用椭偏技术研究了嵌入在SiO2基体中Si纳米晶的尺寸对其复介电函数的影响[111]。使用超晶格方法制备了该样品,通过改变SiOx层的厚度实现了Si纳米晶尺寸的调控。此复杂体系采用三介质模型描述,依次为:c-Si衬底/nc-Si∶SiO2超晶格层/SiO2层。其中nc-Si∶SiO2超晶格层的复介电函数使用Maxwell-Garnett模型进行拟合。 6.2.3 Bruggeman模型 Bruggeman模型εh=〈ε〉,这是一种自洽的假设,有效介质即为基质材料。用于拟合组成复合材料各组分含量相近,无法分辨掺杂物和环境介质的情况。其物理模型如图34(b)所示,表达式为: (47) Bruggeman模型最常用来描述复合材料各组分随机组合的情况,材料表面粗糙层就可用Bruggeman模型进行建模(50%真空和50%底层材料)。文献[86]、[98]、[101-103]、[106]和[112]中的表面粗糙层的光学性质均采用了Bruggeman模型建模(50%真空和50%底层材料)进行描述。不同介质界面处的过渡层也常用此模型建模。例如:文献[102]中两种介质之间的过渡层就采用Bruggeman模型拟合,拟合时选取的比例为:50%上层介质和50%下层介质。 通常使用Bruggeman模型拟合表面粗糙层时均采用50%真空和50%底层材料的比例形式。但在某些情况下拟合时选取的比例也可能不是1∶1。例如:2009年K.Takeuchi和S.Adachi在研究β-Sn薄膜的光学性质时[113],建立了四层膜的光学模型:Si衬底/β-Sn薄膜/表面粗糙层/大气环境(如图35所示),拟合表面粗糙层时使用的是Bruggeman色散模型,该层包含两种组分:β-Sn介质和大气,其中β-Sn介质所占比例为67%。 图35 β-Sn薄膜样品的光学模型示意图[113] Fig.35 Schematic of the layer structure for the β-Sn film sample[113] 椭偏技术由于具有非接触、灵敏度高、无破坏性和测量速度快等优势,所以常常作为薄膜测量工具广泛应用于现代半导体工业中。随着半导体薄膜生长工艺的日新月异,薄膜的厚度越来越薄;所使用的薄膜材料也更加多种多样;薄膜结构也能变得更加复杂;与此同时,很多加工工艺已经进入纳米级别,故而对于椭偏技术的要求也越来越高。下面对椭偏技术未来发展方向做简要的展望与分析: 椭偏技术从Drude提出其测量原理以来对测量的准确度一直有着很高的要求。椭偏测量的准确度已经从1%提高到了0.1%[7],但仍不能完全满足现代工业生产的需求,需要得到进一步的提高。 除了从椭偏原理的研究与发展之外,根据前文对椭偏技术原理及参数分析的介绍可知,椭偏技术是间接测量手段,其准确度依赖于椭偏参数分析阶段对样品建立光学模型的符合程度,尤其需要考虑当前研究条件下是否需要加入界面层和表面粗糙层对椭偏参数拟合结果的影响。同时,为当前测试波段和环境条件下的材料选择合适的光学色散模型也是对拟合结果准确性的保证。 必要时可以结合其他薄膜测量技术,同时评估多平台的测试结果以保证测量结果的准确性。例如:多数时候使用椭偏技术拟合薄膜的光学常数时,可以根据同步拟合获取的膜厚数据和TEM测试的膜厚数据进行比较,判断建立的光学模型和选取的光学色散模型是否准确。2015年和2017年,复旦大学的Z.Y.Wang(王子仪)和D.H.Li(李大海)等人就先后利用此方法检验了拟合结果的准确性[86,96]。除了TEM测试,椭偏技术还经常与XRD[84]、AFM[73,86,96]、Raman[73]等测试手段联合使用。图36是近年来椭偏技术和其他表征技术“合作情况”的统计图。 图36 用于分析(a)薄膜和(b)纳米结构的椭偏技术和其他表征技术“合作情况”的分布统计图(AFM:原子力显微镜;SEM:扫描电子显微镜;TEM:透射电子显微镜;XPS:X射线光电子能谱;XRD:X射线衍射光谱)[114] Fig.36 Distribution of techniques corroborating spectroscopic ellipsometry(SE) for analysis of (a)thin films and (b)nanostructures(AFM:atomic force microscopy; SEM:scanning electron microscopy; TEM:transmission electron microscopy; XPS:X-ray photoelectron spectroscopy; XRD:X-ray diffraction)[114] 在实际应用中,其他测试手段的测试结果除了可以对椭偏拟合结果的准确性进行验证,还常常可以辅助椭偏参数拟合阶段光学模型的建立。例如:利用AFM表征可以获得薄膜表面粗糙层的厚度。获得的粗糙层厚度数据一方面可以进一步用于拟合;另一方面,研究人员还可以根据膜厚大小判断该厚度的表面粗糙层是否会对薄膜性质产生影响,而进一步决定是否在光学模型中加入该层[96]。利用XRD测试可知材料的结晶情况,2015年,Indian Institute of Technology Madras的M.Ghosh和L.Pradipkanti等利用XRD测试获取了氧化石墨烯层间结合水全部除去所需的退火温度,高于该温度的椭偏参数拟合模型中就没有考虑水层[84]。 除了图36中所列举的薄膜表征手段,还有一些可用于薄膜性质检测的技术。例如:超快光谱技术[115-116](Ultrafast Spectroscopy)和光致发光技术(Photoluminescence Spectroscopy)[117-118]。利用椭偏技术可以分析得到材料的能隙,但无法直接获得其能级上载流子的动态信息,例如:电子的转移和耦合,激子的分离等。而超快光谱技术已成功实现对于载流子动态信息的测量,例如:用于低维材料如超晶格、量子阱、量子线等结构对载流子的限制作用所带来的新现象的研究;用于二维材料异质结中载流子的跃迁和弛豫过程,激子分离过程的研究[119-121]。PL技术可测定半导体材料的带隙或杂质能级及其缺陷位点[122],通过将PL技术与激光或时间分辨光谱结合,也可用于研究表面的分子迁移和电子转移过程,光生电子和空穴的复合过程[117]。与此同时,超快光谱技术和PL技术广泛应用于二维材料中激子特性的研究[119],所以在未来对二维材料及其构建的异质结结构带隙性质,载流子输运,激子分离等性质的研究中,有望将椭偏技术与二者相结合,比较椭偏技术与PL技术对材料带隙参数的测试结果,并使用超快光谱技术和PL技术进一步对异质结结构中材料载流子和激子的动态过程进行研究,使研究内容更加完整及丰富。 在椭偏测量数据的处理方面,P.H.Mao(毛鹏辉)等人[123]提出了一种旋转起偏器及检偏器椭圆偏振仪的误差分析与算法,有助于提高测量准确度。以Au块状样品为例,对该方法进行了验证。结果表明,通过提高偏振态的采样率,可以单调地减小离散傅立叶变换(DFT)引起的系统误差。为了进一步提高仪器在相同采样频率下的测量精度,提出了一种自洽椭偏参数差分布的线性拟合逼近方法,可以有效提高测量参量的准确度,并进行了理论模拟和实验测量,两者结果相吻合。 通过建立椭偏技术与其他测试手段的“合作”,无论是辅助建模还是比较多平台的测试结果,最终都可以有效地提高椭偏参数拟合的准确度,并互相补充研究内容,使研究更加完整及丰富,为材料之后的应用奠定坚实的理论基础。 随着材料科学的不断发展,不少新材料的性质(如能隙等)出现在红外或紫外波长区域[124-125]。并且随着薄膜加工工艺的发展,薄膜的结构越来越复杂,出现了多层膜结构和纳米结构的应用[34]。这些都要求寻找较高强度的红外光源,拓宽椭偏仪的测试光谱范围[37]。 而随着技术和理论的发展,椭偏技术今天已经能够完成从远红外到真空紫外的广泛波段的测量[124-125]。如:IRSE(远红外椭偏仪)测量波长可达1 850 nm甚至更高[124],而VUVSE(真空紫外椭偏仪)测量波长可达135 nm[125]。例如:2014年中国科学院长春光学精密机械与物理研究所的王珣等在总结并讨论极紫外光刻技术中有关极紫外光学器件受辐照污染的一些常用的“在线”检测方法时[126],就介绍了一种将椭偏仪与保偏光纤结合起来的保偏光纤椭偏仪。该椭偏仪的结构如图37所示。 图37 基于光纤的椭偏仪结构图[126] Fig.37 Structural diagram of fiber-based ellipsometry[126] 保偏光纤偏振光谱仪将椭偏仪与保偏光纤结合起来,既利用了椭偏仪的优点,同时引入保偏光纤很好地将光传递到样品上,是目前最适合用于EUV光刻系统中使用的“在线”污染检测技术。 此外,太赫兹(THz)射线由于普遍存在,脉宽短(皮秒量级),所以方便时间分辨方面的研究。同时,许多生物大分子的振动和转动能级、许多材料的声子振动能级位于太赫兹波段的范围(包括:电介质材料、半导体材料、超导材料和薄膜材料等),且THz光子能量低对样品伤害较小,因此利用THz时域光谱技术探测材料在THz波段的吸收光谱,进一步应用于对物质结构与物性进行分析和鉴别。基于THz的种种潜力,研究人员也一直致力于将椭偏仪的测试波段进一步延伸到THz,基于THz椭偏仪可以测试介电材料的“Soft Modes”[127]、复杂生物组织[128](如:DNA[129]、人类疤痕[130]等)、自旋振动[131]、反铁磁共振[132]、铁电领域[133]等。但是将椭偏仪在THz波段的设计面临了严峻的挑战:首先,精确控制和操纵偏振器件比较困难;其次THz的发射源一般使用Hofmann T等人[134]设计的一次反向波振荡器(Backward Wave Oscillator,BWO),但是BWO需要抑制驻波,从而避免斑点的形成;再者基于自由空间偏振光谱仪的入射角难以灵活的控制。就以上存在的问题,香港中文大学的X.Q.Chen和E.P.J.Parrott等人于2018年设计了一个全光纤时域THz椭偏仪(Time-Domain Spectroscopic,TDS)[135]。该设计对椭偏仪的入射角控制具有良好的鲁棒性和精确性,并提出算法来精确补偿相位偏差并限制偏振片的消光比(Extinction Ratio,ER)。但是THz TDS的数据常常需要调整以去除来自衬底厚度干涉的回波脉冲,这种调整限制了光谱分辨率。同年同期瑞典Linköping University的Philipp K.和Nerijus A.等利用傅立叶变换将THz TDS转换到频率域[136],该椭偏仪称为频域THz椭偏仪(Frequency-Domain Spectroscopy,FDS)。该设计基于传统RAE的原理并加入其他元件(如图38所示)。该THz FDS可以完成标准和广义的多角度椭偏测试,并且给出了BWO驻波抑制和频率校对的方法,并利用该THz FDS完成了各向异性材料介电常数的测试。由此看来THz波段椭偏仪的性能提升和应用研究还有待研究人员进一步探索。 图38 (左上)THz FDS椭偏仪的俯视图;(右下)THz FDS椭偏仪的技术制图的俯视图与主要组件(不包括吸波泡沫板和外壳)[136] Fig.38 (Top left) Photograph(top view) of the THz FDS ellipsometer.(Bottom right) technical drawing(top view) of the THz FDS ellipsometer with major components indicated and without absorbing foam sheets and housing[136] 椭偏仪测量波段的扩展也是椭偏技术未来的必然发展趋势之一。 椭偏技术在物理、化学、材料科学、微电子技术、薄膜技术、表面和界面技术等方面的应用已经成熟。椭偏技术发展至今,在工业、生物学、医学以及航天技术方面也得到了越来越多的应用。同时,椭偏技术研究的对象也从固体样品扩展到液态样品,促进了生物科学以及医学方面的应用[137],如:与CCD技术相结合实现对生物芯片的研究[137],对蛋白质膜层吸收的研究[138-139],对微生物的研究与辨别等[140]。 近几年,随着纳米加工技术日渐成熟,用户对于器件性能的要求也越来越高,即追求器件的柔性和微型化并进一步向可穿戴式演变,这使得研究人员对二维材料和光子晶体的关注度也随之攀升。而实现该材料应用的前提是了解其性质,椭偏技术因其高精度和非接触等优势被广泛应用于二维材料和光子晶体光学性质的研究。早在2006年,来自台湾的C.H.Lin和H.L.Chen等人就使用椭偏技术结合严格耦合波分析(Rigorous Coupled-Wave Analysis,RCWA)对电子束光刻法制作的硅棒二维平方晶格光子晶体试验样品的光学性质进行了研究[141],模拟出了该样品的反射光谱,直接反映了其光子带隙。而二维材料的种类十分丰富,关于光学和电学相关应用研究的热门材料主要为石墨烯[66,142]及过渡金属二硫化物(Transition Metal Dichalcogenide,TMDs)[73]。使用椭偏参数可以判断所研究二维材料的原子层数信息,进一步分析可得其光学常数[143]。 但是,由于二维材料厚度极薄(原子级别)并且具有吸收性质,所以使用光学色散模型拟合椭偏参数(ψ,Δ)期望同时获取该薄膜的厚度和光学常数(n,k等)比较困难会出现数据的耦合而降低椭偏测试的灵敏度,在椭偏参数测试时可以使用干涉增强法改善[142]。此外,在椭偏参数拟合时使用点对点方法也可以较准确获得薄膜光学常数,但是使用此方法拟合之前需要较准确地获取薄膜的厚度,可借助TEM等薄膜表征手段[73]。 另外需要注意的是光子晶体具有各向异性,其光学常数与方向有关。此时,对于这种复杂结构薄膜的测试可以使用穆勒矩阵椭偏仪。穆勒矩阵椭偏仪与传统椭偏仪相比,前者测量了样品的全部穆勒矩阵参数(传统椭偏仪只测量部分穆勒矩阵元素),因此可以测量获得样品更加丰富的信息(如:各向异性),该类型椭偏仪被广泛运用于微纳结构的测量,包括:光子晶体和光栅等[31-32]。并且由于其非接触、非破坏和高精度等优点,在复杂结构分析上比传统SEM、AFM和激光衍射(Laser Diffraction,LD)等技术更有优势[144]。2017年,挪威NTNU Norwegian University of Science and Technology的J.P.Banon和I.Simonsen等人[145]使用穆勒矩阵椭偏仪、减瑞利方程(Reduced Rayleigh Equation,即RRE)并结合一个优化方案完成了等离子体光子晶体临界尺寸测量(研究样品为:熔融二氧化硅作衬底表面排列半球状金粒子构成的二维光子晶体)。 图39 双旋转补偿器型穆勒矩阵成像椭偏仪测量原理示意图[146] Fig.39 Scheme of the dual rotating compensator Mueller matrix imaging ellipsometer[146] 在此基础上,2016年华中科技大学数字制造装备与技术国家重大实验室,又进一步将穆勒矩阵椭偏仪与显微成像技术相结合发展穆勒矩阵成像椭偏测量技术(Mueller matrix imaging ellipsometry,即MMIE)并将其用于纳米结构几何参数的大面积测量[146],其结构如图39所示。 MMIE突破了椭偏光谱测量技术和穆勒矩阵椭偏测量技术横向分辨率由测试时照射至样品表面的光斑直径和样品台移动精度决定的瓶颈。具有对整个视场内的各个像素点进行大面积独立测椭偏参数的能力,由此可以实现对样品状态的实时观测并重构其三维显微形貌,同时准确地确认被测区域。这样一来,首先在保证纵向分辨率(通常指膜厚测量精度为埃级)的情况下,优化仪器的横向分辨率(可达几个微米量级甚至光学衍射极限水平);其次,提高了对大面积样品的分析测试效率。 磁光椭偏技术是近几年发展起来的新技术,它可以实现在一台仪器中对磁性材料磁光性质与光学性质的同时测量(同时测得材料的磁光耦合系数和复折射率)[147]。磁光椭偏技术结合了磁光克尔效应(Magneto-Optical Kerr Effect,MOKE)与椭偏技术,通过探测克尔效应引起的反射光偏振状态的改变,从而给出体材料和纳米磁性膜的磁光特性(如:材料的磁化方向),对研究磁性材料的磁各向异性、磁耦合等具有重要的意义,具有良好的发展前景。例如:和磁控溅射设备结合,实现在薄膜生长过程中进行原位测量,是检测和指导薄膜生长的重要工具;还为现有磁光薄膜材料的升级和寻找新型磁光材料提供可靠的理论与实验支持。但是由于纳米薄膜材料太薄,使用磁光椭偏仪测试时,得到反射光偏振态的变化很小,其携带的磁致反射信号也就很小,信号信噪比较低。因此纳米薄膜的磁光椭偏技术面临着微弱信号检测以及提高信噪比两大问题[148]。磁光椭偏仪也是未来椭偏仪的一个重要分支,期待该技术的进一步完善和提升。 椭偏技术应用领域的拓宽是未来椭偏技术应用的一个最重要方向。同时,应用领域的拓宽也催化了科研人员们对椭偏仪性能提升的探究。 从椭偏测量方法诞生至今,研究人员们对于椭偏技术测量速度的提高、测量时间的缩短的努力未曾停止过。就应用最广的光度式和消光式椭偏仪来说,两者都可以采用如图4所示PCSA的结构,测量时都需要转动P、C或A的方位角,这一过程可以手动完成;也可以借助计算机程序操纵机械转动;还可以应用电光调制或光弹技术进行无机械转动的相位调制椭偏测量,对比之下,运用非机械转动的偏振态变化原理完成测量的速度显然是最快的。所以,真正决定椭偏测量速度的是测量的自动化程度[45]。除了上述的方案之外,研究人员还提出了很多提升椭偏仪测试速度的设计,例如:引入能够同步进行数据获取和处理的控制系统有效缩短测量时间,或者利用优化算法较快求出参量等等,都有利于增强椭偏仪的在线检测和控制功能[37]。加快椭偏仪器的测量速度一直是研究人员努力的方向之一。 除了常用的使用空间分辨椭偏仪分析薄膜样品不同位置处的光学性质,时间分辨椭偏技术也是近几年热门的研究方向。时间分辨光谱分析可以记录一段时间光谱随时间的变化,进一步分析了解在各个瞬时状态薄膜材料的性质,从而记录材料性质变化的过程。可用在工艺生产中薄膜制备过程的监测,实时掌握薄膜状态。 椭偏技术因其具有非接触、高精度、非破坏性的特性,并且能够获得包括样品的光学、电学、结构(多层结构)、化学组分等信息的综合测量特点受到了广泛应用。 椭偏原理首先由Drude教授在19世纪末提出。初期阶段,科学家们主要使用手动消光式椭偏仪进行测试,但是测试的精度和速度等并没有明显的优势,所以应用和推广受到了限制。直到1973年计算机技术与椭偏技术相结合,光度式椭偏仪进入人们的视野,测试的准确度、数据处理及运算速度都有重大飞跃,从此椭偏技术得到了国内外学者的广泛关注和应用。与国外的椭偏研究相比,国内的发展虽然起步有点晚,但是发展相当迅速。 椭偏仪(反射式)是测量线偏振光经材料表面反射后,光的相对振幅与相位改变量的仪器。根据测试原理的不同,主要分为消光式和光度式两类。光度式椭偏仪测量速度明显快于消光式椭偏仪,特别适用于在线检测和实时测量等工业领域。椭偏仪种类繁多,例如:旋转偏振器件型椭偏仪、相位调制型椭偏仪、成像椭偏仪和广义椭偏仪等。其中,旋转偏振器件型椭偏仪包含:RAE、RPE、RAP、RPAE和RCE等不同形式。相位调制型椭偏仪使用光弹性元件,不需要机械转动即可进行测试,进一步提高了测试速度。椭偏光谱仪可以实现多波长的椭偏测试;红外椭偏光谱仪将椭偏测试波段扩展至红外波段,多用于多层膜和复杂结构的测试;成像椭偏仪有效地提高了椭偏仪的空间分辨率;广义椭偏仪可用于各向异性材料的测试。并且各种椭偏仪优缺点各有不同,可根据实际测试需要进行选择。 椭偏测量是间接测量手段,通过椭偏测试可以获得样品的椭偏参数(ψ,Δ),而样品的光学常数(包含复介电函数)和吸收率等相关光学性质的获取需要进一步对椭偏参数进行拟合。椭偏参数的拟合步骤根据样品的不同也不尽相同。体材料椭偏参数可以直接使用Snell和Fresnel公式进行拟合,相对简单。而薄膜材料椭偏参数的拟合较为复杂,基本步骤为:测量、建模和拟合。首先依据样品结构建立对应的光学模型(常为多层膜结构),然后根据每层材料的光学性质选择恰当的光学色散模型进行拟合。最后为了检验拟合结果是否正确,计算均方误差(MSE)来判断拟合值相对测量值的偏离程度,全局最小的MSE对应的拟合数据即为最佳结果。通常还需要验证拟合数据是否满足K-K关系。特别地,例如薄膜结构较为复杂,难以选择合适的光学色散模型进行拟合等情况时,常常采用数学反演的方法来获取椭偏测量的光谱范围内待测材料的光学常数。 椭偏参数拟合步骤常用的色散模型有:Lorentz模型、Sellmeier模型、Cauchy模型、F-B模型、Tauc-Lorentz模型、Drude模型和有效介质近似模型(EMA)。前6种光学色散模型适用于不同性质的单一均匀介质,而EMA模型适用于多种介质混合构成的复杂材料光学性质的描述。EMA模型根据基质材料选择的不同又可以分为3种:Lorentz- Lorentz模型、Maxwell-Garnett模型和Bruggeman模型,分别适用于不同种类的复合材料。 随着加工工艺、生产及测试标准和需求的提高,对椭偏技术提出了许多新的要求。椭偏技术未来的发展趋势主要有:测量准确度进一步提高、测量波长范围进一步扩大以及椭偏技术应用领域进一步拓展等。 椭偏技术内涵丰富,可以和其他技术相结合,进一步提升椭偏仪的性能和应用范围。椭偏技术是薄膜材料重要的测试手段之一,利用该技术可以获得材料的基本性质,如:厚度、光学常数、介电常数、带隙等。利用这些薄膜材料的重要参数,研究人员可以进一步完成功能化薄膜体系的设计,或者分析薄膜体系深层次隐藏的物理机制。相信研究人员们未来对于椭偏技术的更新和应用的探索将促进椭偏技术进一步的创新及发展,并且利用椭偏技术研究获得更多有利于人类社会发展进步的新成果。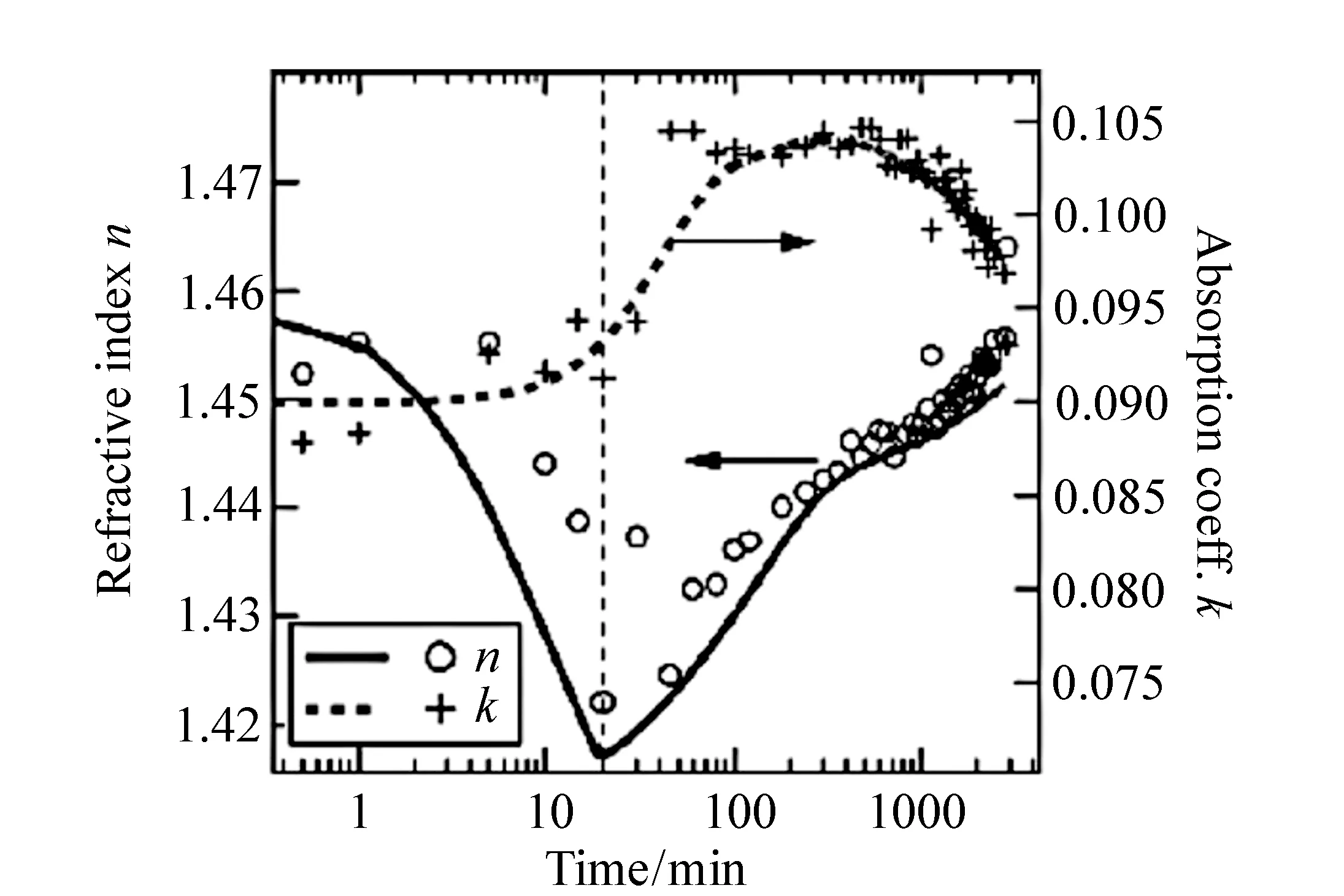
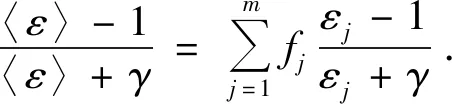


7 椭偏技术的发展方向
7.1 提高测量准确度
7.2 扩大测量波长范围

7.3 拓宽椭偏技术应用领域
7.4 其他发展方向
8 结束语
