“设线”还是“设点”，这是一个问题——对近三年浙江卷解析几何的几点思考

浙江省安吉县高级中学 (313300) 魏侹路

今年高考结束后，笔者和几个班上程度较好的学生交流了一下对今年数学试卷的感受．大家普遍感觉最后两题难度很大，特别是解析几何，虽然问题看上去也很常规，可就是怎么算都算不出来．在笔者询问了他们的方法之后，发现多数人是选择了从设直线AB入手，只有少数人是像参考答案给出的一样设点A的坐标．那么，设直线AB入手到底是否可行呢？笔者尝试后给出了下面解法．

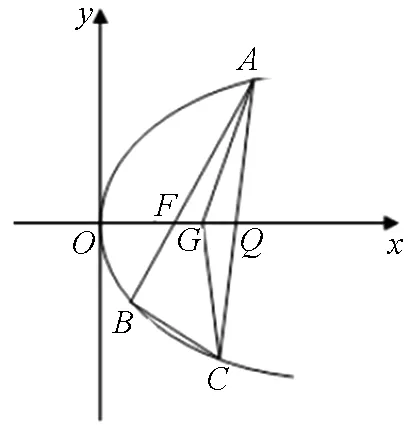
图1

一、考题再现

(2019浙江第21题)如图1，已知点F(1，0)为抛物线y2=2px(p>0)的焦点，过点F的直线交抛物线于A、B两点，点C在抛物线上，使得△ABC的重心G在x轴上，直线AC交x轴于点Q，且Q在点F的右侧．记△AFG,△CQG的面积分别为S1,S2．

(1)求p的值及抛物线的标准方程；

解法一：(1)p=2,y2=4x；

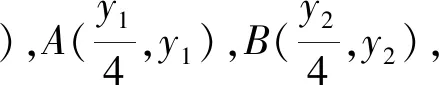
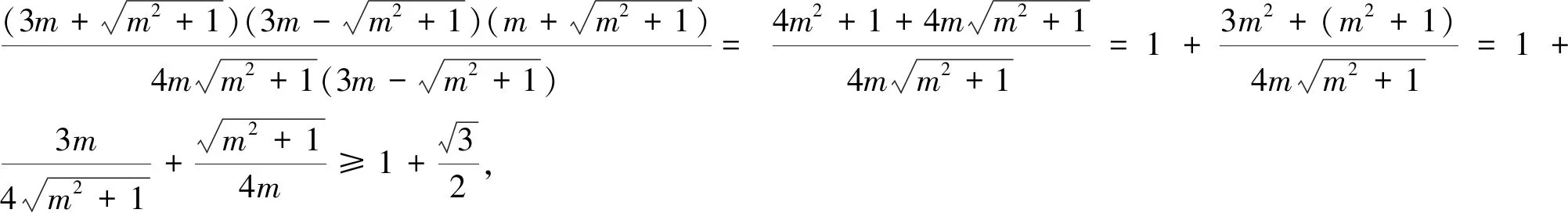
这种解法过程中我们可以发现，由于求面积的过程中涉及到了点A的纵坐标，我们是利用了求根公式将其解出．这不同于我们通常设直线方程后“设而不求”，利用韦达定理整体计算的一般做法，因此整个过程计算量非常大．这对于考生而言，在考场上近乎是不可能完成的任务．那么，如果一开始不是从直线AB的方程出发，而是改从点坐标入手，这就是参考答案给出的思路，下面笔者给出另一种设点坐标的解法．

图2

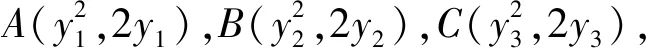
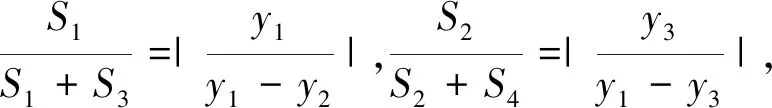
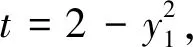
比较两种解法可以发现，解法二的运算量明显会比解法一小一些，所以相对于此题是较优的方法.但是我们也要注意到，设点坐标的过程中，难点在于如何将面积比值转化到点A,B,C的坐标上来，而解法一中面积比值的计算思路是比较直接的.所以解法二运算量减少的“代价”是思维量的提升.

二、回顾真题

可以说今年的高考解析几何是设点坐标的解法较优，那么之前几年的情况又如何呢？我们可以看到，2018年的高考解析几何参考答案给出的做法依然是设点坐标，那设直线入手是否可行呢？

图3

(2018浙江第21题)如图3，已知点P是y轴左侧(不含y轴)一点，抛物线C：y2=4x上存在不同的两点A，B满足PA，PB的中点均在C上．

(1)设AB中点为M，证明：PM垂直于y轴；

通过比较上述设直线求解与参考答案设点的求解方法后可以发现，设点的做法计算量较小.因为在设直线的做法中无法回避还要设出点A,B,P的坐标，导致参数数量增加了两个，这对于学生的运算化简要求更高.所以，此题依然是设点的做法较优.

接下来我们再回顾一下2017年的高考解析几何，当年此题参考答案给出的做法是设直线，那从设点入手又是否可行呢？

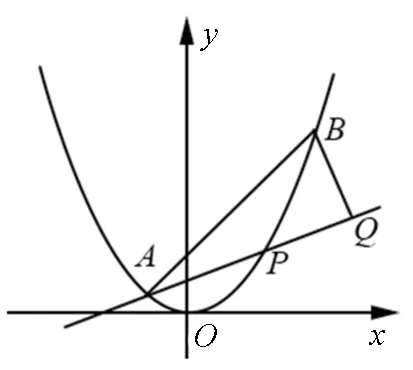
图4

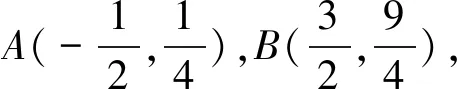
(1)求直线AP斜率的取值范围；

(2)求|PA|·|PQ|的最大值．

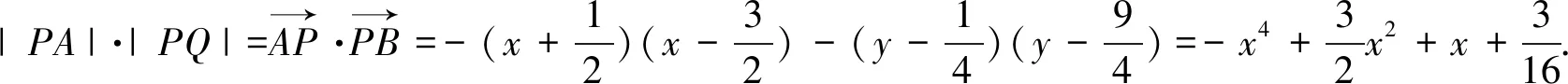
本题设点的做法运算量比设直线大大简化，但是这又是以思维量的提升为“代价”的，因为如何将|PA|·|PQ|转化到点A,B,P的坐标上来是一个难点，这里是借助向量这一工具实现了转化.所以，此题依然是设点的解法较优.

三、几点思考

1.“设线”还是“设点”该如何选择

回顾近三年的高考解析几何我们发现，无论是“设线”还是“设点”，一般都是可以做的.但是这三题的运算量都是“设线”时大一些，那么什么情况下我们选择“设线”时好一些呢？笔者以为，关键要看所设直线能否方便的将“问题所需量”与之联系起来.2019年中的问题是△AFG,△CQG的面积比值，“问题所需量”就是点A,F,G,Q,C的坐标或是相关长度、距离，但是设直线AB却无法直接联系点Q的坐标.而且，问题只需要点A，不需要点B，不利于“设而不求”运算的进行.因此，“设线”不是最佳方案.此题2018年中的问题是△PAB的面积，“问题所需量”就是点P,A,B的坐标或是相关长度、距离，设直线AB无法直接联系点P的坐标.因此，“设线”也不是最佳方案.2017年中的问题是|PA|·|PQ|，“问题所需量”就是点A,P,Q的坐标或是相关长度、距离，设直线AP较容易联系三个点的坐标或是相关长度、距离.因此，参考答案给出的是“设线”的方案.本文中给出的做法虽然运算简洁，但需借助向量，并非所有考生都能想到.在考场时间有限的环境下，“设线”的做法仍不失为首选方案.所以，当所设直线能够方便的表达出“问题所需量”时，“设线”应当是我们采取的常规手段.当所设直线不能够方便的表达出“问题所需量”时，我们考虑“设点”.

2.“设点”在椭圆中是否可行

我们注意到这三题的背景都是抛物线，所以“设点”都比较方便，那么若是椭圆的背景下，“设点”的做法还行得通吗？那么我们来看下面这个问题.

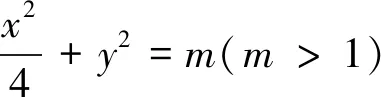
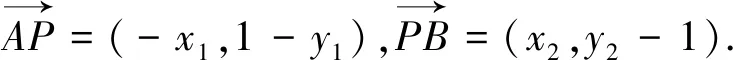
可以看出，“设点”的做法在近三年的浙江高考解析几何中都可以解决问题，即便是椭圆的背景下也不例外.

3.“设线”还是“设点”，运算的核心是什么

点、直线、曲线作为几何中的基本图形，构建起了我们研究的解析几何对象.解析几何的基本方法是坐标法，因此，我们研究解析几何图形中的众多关系，最终都是将其转化成为点的坐标、直线或曲线方程中的有关系数等变量.无论是“设线”或是“设点”的做法，运算的核心都是在建立起众多变量之间的联系.例如，在2019年的21题解法一中，问题最终转化到变量m上去.参考答案及解法二中，问题最终转化为点A的纵坐标这一变量.

一般来说，“设线”时至多只有两个变量，当所设直线能够方便的表达出“问题所需量”时，“设线”具有变量少、运算思路简洁的特点.而“设点”相对而言变量更多，变量间的关系更复杂，对学生的运算能力要求更高，但思维量的提升往往能带来运算量的降低.特别是当直线无法方便的将“问题所需量”与之联系起来时，“设点”往往是较优方案.

4.“设线”还是“设点”，学生的障碍在哪里

数学运算是指在明晰运算对象的基础上，依据运算法则解决数学问题的素养.数学运算主要表现为：理解运算对象，掌握运算法则，探究运算思路，求得运算结果.学生在日常的学习过程中比较关注的是运算法则和运算结果的正确性.但对运算对象的理解，运算思路的探究往往忽视.而“设线”还是“设点”，这个问题的关键恰恰在于学生选取什么量将题目中的信息联系起来，如何才能将已知信息转化到所设变量上去.这恰恰是学生算法思想的体现.因此，在今后的日常教学工作中，笔者应当加强学生对运算对象的理解和对运算方法的优化.通过让学生探究不同的算法，经历不同的运算过程，在比较中养成对运算思考的习惯，从而发展他们的数学运算这一核心素养.