嵌入社区半径的力引导与径向树混合布局算法

任淑霞， 吴 涛， 张书博

(天津工业大学计算机科学与软件学院， 天津 300387)

1 引 言

计算机技术的快速发展，让社会关系网络、生物网络、疾病传播网络等网络分析在现实生活中起到重要的作用.但要正确地解读和理解这些网络中包含的信息却非常困难.因此，如何描绘网络和节点结构，让其便于理解和使用一直是复杂网络布局算法领域研究的热门.

最早对复杂网络进行布局的是1984年Peter Eades提出的弹力模型[1].Eades的算法虽然简单，但是效率非常低.Fruchterman和Reingold提出FR(Fruchterman-Reingold)[2]布局算法.FR算法易于实现、降低了计算复杂度.由于FR算法强调节点均匀、边长一致等美学标准，因此上述改进算法均存在阻碍网络社区结构形成的缺陷.

于是，学者开始关注于将聚类方法应用于布局算法的研究，Linlog模型[3]是一种计算最小能量来呈现社区结构的模型，虽然它已经实现聚类效果，但没办法证明社区划分的有效性.吴渝等[4]提出了社团引力导引的布局算法，该算法不仅为每个节点加入社团引力，还结合K-means算法让节点向社团的中心位置聚拢，该算法无需对节点分类，可以在布局的同时对节点聚类.Zhou等[5]提出了基于度中心性的社团力导引改进算法，从而完成对复杂网络的聚类布局.通过观察发现聚类布局算法均能达成社区划分且社区之间没有重叠的效果.但是，社区内的节点由于太过靠拢，用户很难发现社区内节点之间的关系，不利于用户对社区内部的信息的探索.

基于上述问题，本文提出嵌入社区半径的力引导与径向树混合布局算法ERRTH(community radius embedded in force-directed and radial tree hybid layout algorithm)，针对FR布局算法单纯追求美学标准而不利于发现网络中的社区结构这一问题，本文采用K-means算法快速进行社区划分，再用嵌入[6]社区半径的社区引力和斥力来分离社区，从而完成复杂网络社区结构的展示.为弥补聚类布局算法在社区内部节点结构展示上的缺陷，本文混合径向树来层次化显示社区内节点结构.布局结果不仅符合对称性和美学标准，同时也便于用户观察和分析复杂网络中的信息.

2 嵌入社区半径的力引导布局算法

2.1 FR布局算法

FR布局算法是一种力引导图布局算法.它遵循两个简单的原则：有边连接的节点应该相互靠近；节点之间不能离得太近.

FR算法的每次迭代主要分为两个部分：

1) 计算节点之间的斥力

fr(i,j)=-u2/dist(i,j).

2) 计算有边连接的节点之间的吸引力

fa(i,j)=dist(i,j)2/u

其中，u代表两节点之间的理想距离.

最后，综合吸引力和斥力，通过最大位移来限制节点的移动距离.当两个节点存在覆盖现象时，FR算法会施加斥力来分开节点.FR算法在布局时仅仅改变节点位置，避免重叠，并没有分离节点所属的社区，不利于用户的观察.为达到分离社区的目的，本文提出嵌入社区半径的力引导布局算法.

2.2 嵌入社区半径的力引导布局算法

大量研究显示复杂网络存在社区内连边众多，而社区之间连边较少的特性，因此采用社区划分[7]来构建社区网络.当社区数量较多时易产生社区重叠或超出布局区域范围的现象，为解决该问题，本文提出社区半径并定义社区网络的社区斥力和社区引力，同时用社区半径对社区斥力和引力作用范围进行合理限制.

嵌入社区半径的力引导布局算法步骤如下：

(1) 构建社区网络.

采用K-means算法[8]，选取m个点作为m个社区的初始中心点，然后分配节点到最近的中心点所在的社区，重新计算中心点，如果中心点不变，则停止计算；否则继续直到社区中心不变为止.将复杂网络划G(V,E)分出m个社区{H1,H2,…,Hm}，构建社区网络G′.

(2) 计算社区半径.

定义1社区半径ri.社区半径ri是社区Hi以社区中心为圆心的圆的半径，社区内节点越多，ri越大.社区半径的计算公式为

(1)

式中，x和y表示画布的宽和高；num(v)表示网络中的节点数量；Mi表示社区Hi的布局区域.

(3) 计算社区斥力.

定义2社区斥力E(HA,HB)，设社区斥力E(HA,HB)是社区网络G′中社区HA和社区HB之间存在的一种斥力.E(HA,HB)的计算公式为

(2)

其中，l(eAB)表示A、B社区中心的距离；N(HA)表示社区A所包含的节点数.

社区网络中社区之间存在社区斥力，社区斥力主要由社区半径来限制作用范围和计算.由图1可以看出，社区之间的社区斥力主要由l(eAB)和d来确定的.

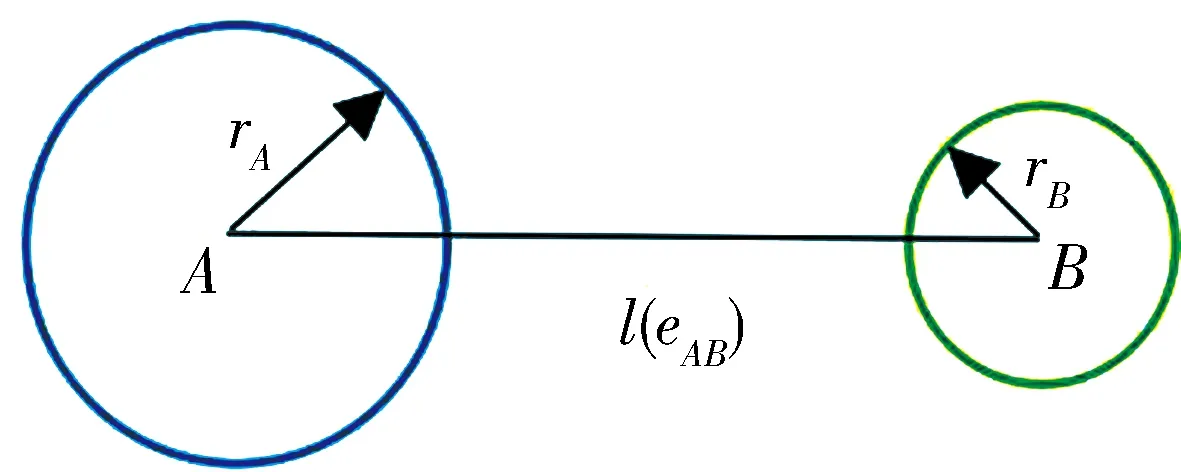
(a) l(eAB)≥2d,d=rA+rB

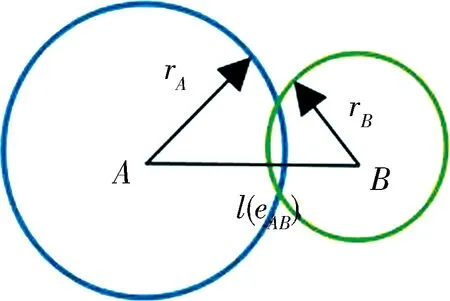
(b) l(eAB)≤d,d=rA+rB

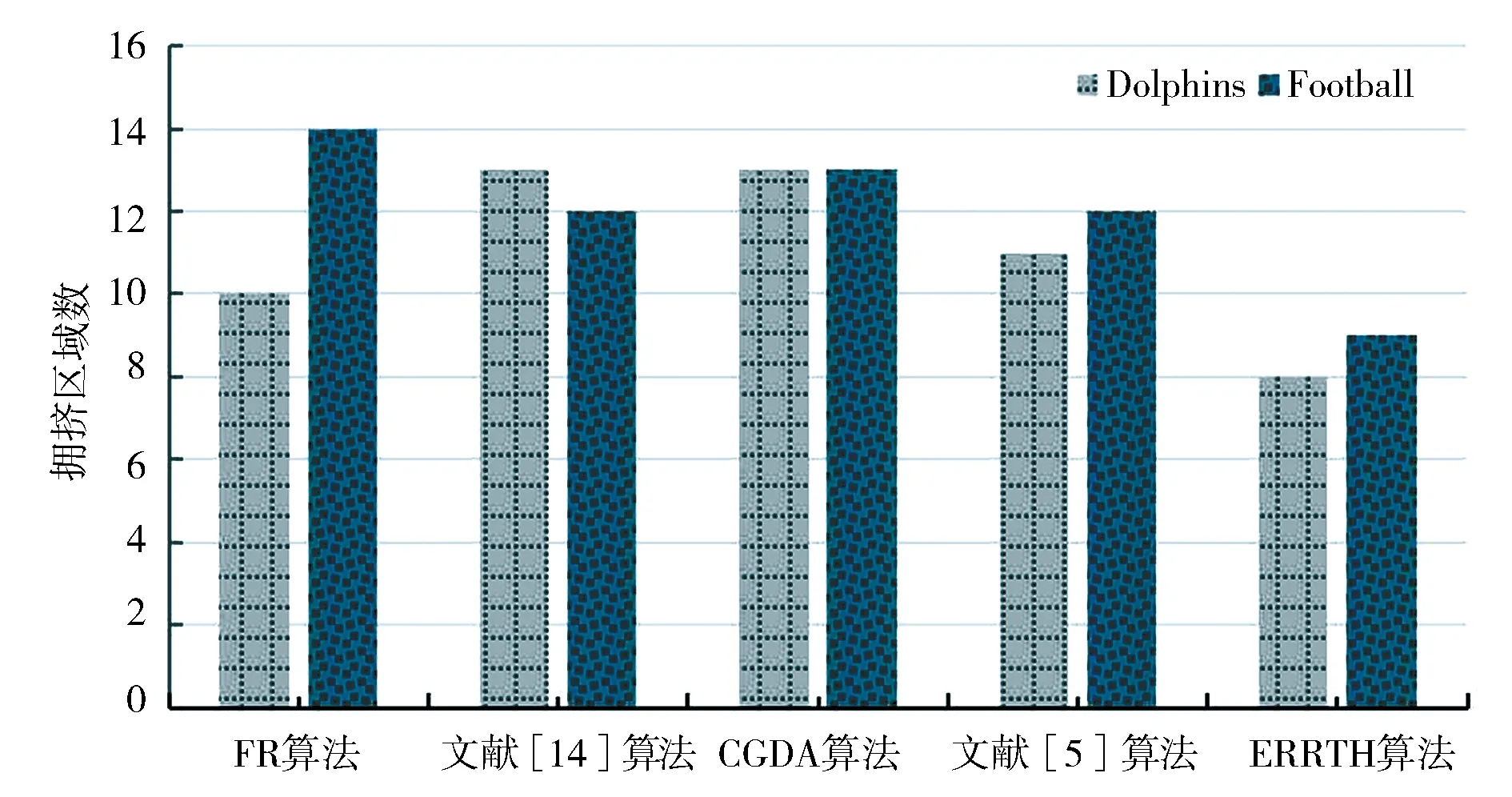
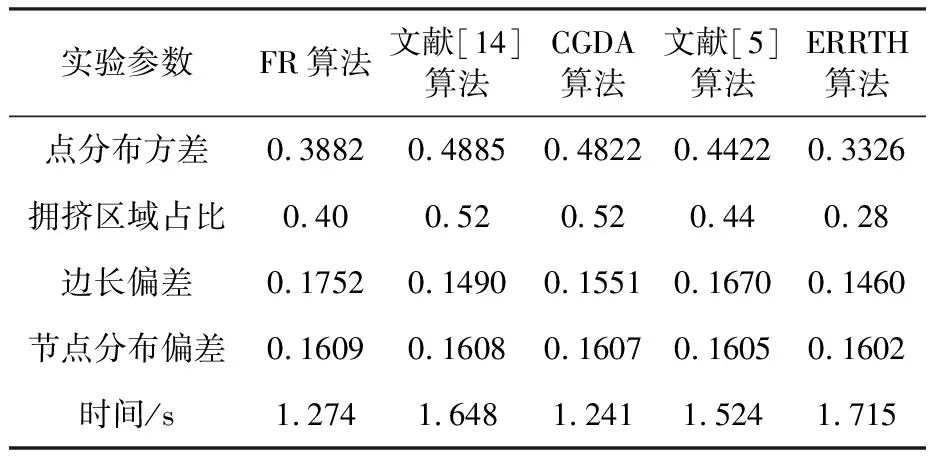
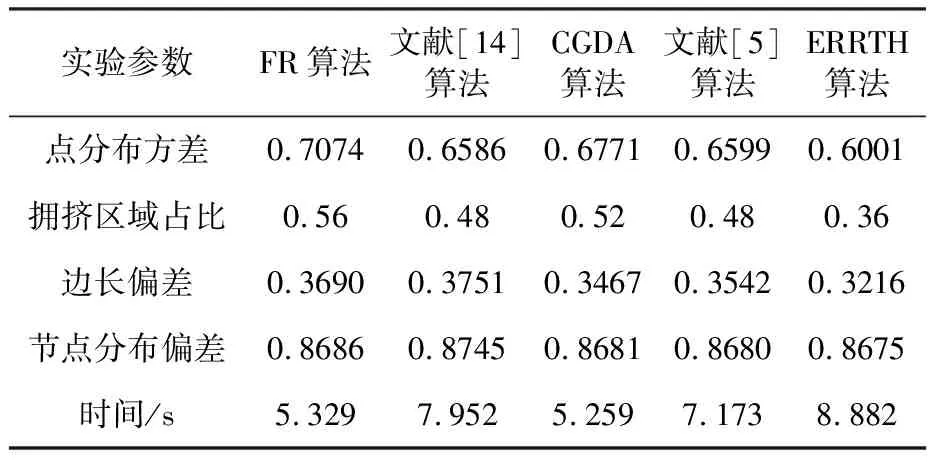
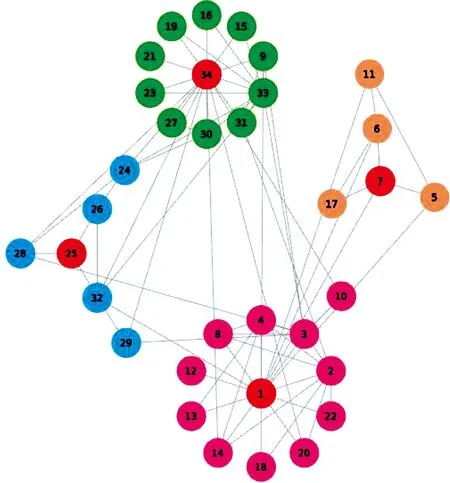
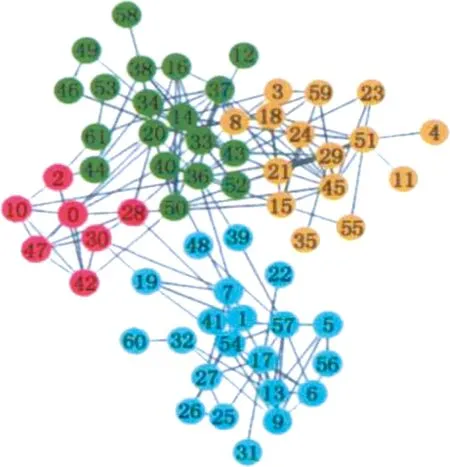
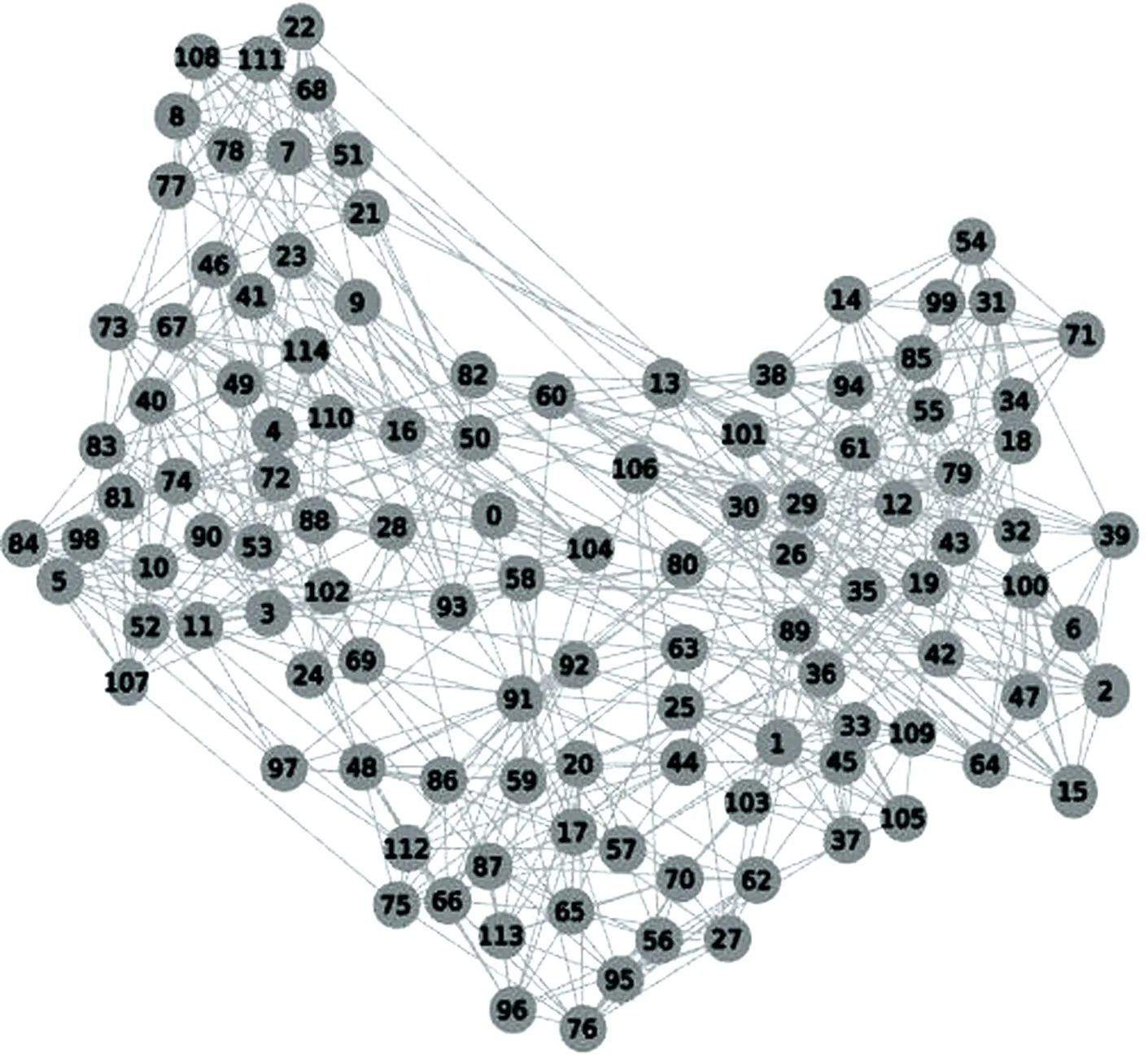
(c) d

1) 如图1(a)所示，当社区中心距离l(eAB)≥2d时，两社区之间应该只有社区引力而没有社区斥力，此时社区斥力E(HA,HB)=0.

2) 如图1(b)所示，当社区中心距离l(eAB)≤d时，两社区会发生社区重叠.因此，需要施加一个固定常量的斥力h来分离两社区，此时社区斥力E(HA,HB)=h.

因此，社区半径能将社区斥力的作用范围限制在[0,2(rA+rB))之间，社区斥力能够分离两社区并阻止它们之间的社区重叠.

4) 计算社区引力.

定义3社区引力G(HA,HB)，社区引力G(HA,HB)是社区网络中社区和社区之间存在的一种引力.G(HA,HB)的计算公式为

G(HA,HB)=

(3)

社区网络中不仅存在社区斥力，还存在社区引力，也由社区半径来限制其作用范围和计算的.如图2所示.

(a) l(eAB)≤d,d=rA+rB

(b)l(eAB)>d,d=rA+rB

1) 如图2(a)所示，当社区中心距离l(eAB)=d时，如果两社区存在社区引力，那么它们将会发生社区重叠，这时只有社区斥力而无社区引力.因此，当l(eAB)≤d时，社区引力G(HA,HB)=0.

2) 如图2(b)所示，当社区中心距离l(eAB)>d时，两社区之间就会存在社区引力.开始时，社区引力与两个社区所包含的节点数之差成正比.随着l(eAB)增大，社区引力将会变大，而社区斥力将变小，社区之间将会吸引来解决超出布局区域的问题.同时，需要存在一个引力系数g，方便用户随时调节社区引力的值来调整布局结果，此时社区引力为

(4)

因此，可得出社区引力的作用范围为(rA+rB,)，社区引力能解决两社区相距太远而超出布局区域的问题.

嵌入社区半径的力引导算法在Karate数据集的布局结果如图3(b)所示.较之FR算法，可以看出复杂网络被划分成不同社区，社区之间相互远离，社区网络的结构明显.但社区内节点相互拥挤在一起，不利于用户观察社区内结构特征与连边关系.因此，本文采用径向树布局排列各社区内节点，让节点满足层次结构布局的需求.

(a) FR算法的布局结果

(b) 嵌入社区半径的力引导算法的布局结果

(b) Layout result of community radius embedded in Force-Directed algorithm

图3 布局结果对比图

Fig.3 Layout result comparison graph

3 混合径向树的社区半径力引导算法

3.1 径向树

树图[9]关注自动生成关系信息的几何表示，通常用于分层可视化.用于对分层信息进行建模的典型数据结构是顶点表示实体并且其连边对应于实体之间关系的树.层次结构布局可以向用户有效的传达信息.径向树[10-11]作为树图的分支，在展示节点结构层次有着独特优势.

3.2 采用径向树排列社区节点

为直观展示社区内节点层次结构，本文采用径向树对社区内的节点进行排列，使所有节点都位于社区中心聚焦的同心圆上.径向树排列节点的步骤如下.

(1) 如要快速搜索出社区内节点的全部层次结构L，则采用DFS(深度搜索算法)来而不采用BFS(广度搜索算法)，并从社区内随机选出节点作为根节点放置在社区中心，设各级之间的距离D是将社区半径除以社区中的级数L来计算的.

(2) 将根节点放置在社区中心，此节点是下一级中其他节点的父节点.由于1级节点具有相同的父节点，可以分布在整个2π上.因此计算角度时，将2π除以1级节点的数量，这会在1级节点之间创建角度空间，然后遍历1级节点，使用式(5)计算1级节点的位置.

(5)

其中，NIwl是层级内的节点索引；As是角度空间.

(3) 计算切线角度.

定义4层级半径.节点所在的层级到根节点的距离叫做层级半径.

节点N0的子节点必须落在其所属层级的一定范围内以防止重叠，切线垂直于N0节点与根节点的连线，切线与子节点所在层级相交的点为切线切点.切线切点与N0节点的父节点(根节点)连线的夹角作为切线角度，使用式(6)来计算切线角度.

TanAn(N0)=2arccos(Rout/Rin)

(6)

式中，Rin是子节点所对应的层级半径；Rout是父节点所对应的层级半径.

(4) 计算等分线角度.节点N0计算等分线角度公式如下.

(7)

其中，N1、N2是N0的相邻节点；Arc(N0,N1)为图4中N0与N1的夹角.子节点所能分配的范围为等分线角度与切线角度的交集所对应的圆弧上，这能避免子节点分配重叠的现象.子节点的分配范围如图4所示.

(5) 在2级或更高级别上，由于父节点限制子节点的位置，首先得到待分配子节点的父节点集合.遍历该集合，得到父节点的子节点列表，明确子节点的分配范围，放置子节点在分配范围对应的圆弧上.

ERRTH算法的最终布局结果如图5所示，较之图3展示的布局结果，可以看出社区内节点层次结构分明，节点之间拥挤程度不高.其中红色节点为根节点，其余节点分布在以根节点为圆心的同心圆上，布局结果明显，且符合对称性和美学标准.

图4 子节点的分配范围示意图Fig.4 Child node allocation range graph

图5 ERRTH算法布局结果

3.3 ERRTH算法步骤

ERRTH算法步骤如算法1所示.

算法1 ERRTH算法

输入：网络G(V,E)，最大迭代次数N，最大位移M.

输出：网络节点位置坐标{D1,D2, …,Dn}.

Begin

1) 初始化节点位置，为节点生成随机的坐标.

2) 用K-means将网络G划分出m个社区，构建社区网络，确定各社区节点数量，依据式(1)计算出社区半径.

3) 依据式(2)和式(3)计算社区网络中社区之间社区引力和斥力，综合社区引力和斥力，用最大位移M限制社区的最大移动距离，社区所属节点随着各社区中心移动.

4) 若迭代次数大于最大迭代次数，执行步骤5)，否则，循环步骤3).

5) 对于社区内节点，用DFS算法明确各社区层级，然后通过社区半径计算出级间距离，放置根节点.

6) 对于社区内1级节点，依据式(5)计算1级节点位置.

7) 对于社区内2级或更高级别的节点，依据式(6)确定切线角度和式(7)确定等分线角度，明确切线角度和等分线角度的交集范围，放置节点到交集范围所对应的圆弧上，循环放社区内节点至最后一层即可.

8) 输出节点位置{D1,D2…,Dn}.

End.

4 实验结果分析

为证明算法的合理性和有效性，本文选用复杂网络中的Dolphins[12]，Karate[13]，Football[5]网络来展示复杂网络社区结构，选取FR算法和朱志良等人算法[14]的布局结果进行对比.为定量分析本文算法的合理性，将ERRTH算法与FR算法、CGDA算法[13]、文献[14]算法和文献[5]算法采用相同数据集进行对比，并用点分布方差[14]、拥挤区域占比、边长偏差[15]、节点分布偏差[16]和时间进行实验分析.实验的运行环境是intenl(R)Core(TM)2 Quad CPU Q8300@2.50 GHz、内存为16 G、64位Win10的PC.

4.1 布局结果分析

(1) Dolphins网络是依据生活在新西兰的62只海豚而创建的社会关系网络，该网络包含62个节点和159条边.

ERRTH算法与朱志良等人的算法在Dolphins数据集上的布局结果如图6所示.图6(a)是文献[14]的可视化布局结果，该算法虽然阻止不同社区节点的交错，但社区位置过于靠近，网络变得非常拥挤，若没有颜色加以区分，用户无法观察出社区结构.而图6(b)可以看出ERRTH算法不仅能够阻止不同社区的覆盖，而且社区之间相互远离且层次结构明显.两者比较，ERRTH算法能清晰地展示网络的社区结构和社区层次结构.

(2) Football网络数据集，该数据集表示美国大学生足球俱乐部比赛的网络，该数据集包含115个节点和616条边.

图7为Football数据集的布局结果，由于数据集节点与边规模比较大，因此选择适当缩小节点来满足布局要求.从图7(a)可以看出FR算法已经不能满足复杂网络展示和美学需求，节点之间层次结构，用户很难明确社区结构和节点层次特征.为了能够在图7(b)中清晰地观察社区结构，本文选择放大蓝色方框内的布局结果如图8所示.

(a) 文献[14]的布局结果 (b) ERRTH算法布局结果

(a) The layout result of document [14] (b) The layout result of ERRTH

图6 Dolphins布局对比图

Fig.6 Comparison graph of Dolphins layout

图8(b)可以清晰显示根节点17与下一层级的20、70等节点相连，而图8(c)节点20与相同层级的62、65、87、70等节点和下一层级的76、75、36等节点相连，用户分析网络时可以优先着眼于社区内部的关键信息，然后再与不同社区的节点联合分析.从而提高用户获得复杂网络关键信息的效率，方便用户的使用.最后，综合图7(a)和(b)可以看出ERRTH算法不仅能够分离不同的社区，还能展示社区内的层次结构和连边关系，便于用户探索复杂网络的信息.

4.2 算法效率分析

4.2.1 时间复杂度分析 ERRTH算法由嵌入社区半径的力引导和径向树布局算法两部分组成.针对嵌入社区半径的力引导布局算法，在每一次迭代过程中，社区网络中的k个社区都要计算各自的社区引力和斥力，社区内的节点v′采用引力的方式随着社区中心移动，所以这部分的时间复杂度为Ο(k2+k|v′|).针对径向树布局，每个社区内的节点都采用DFS算法明确节点层级结构.循环节点层级结构L，依据父节点v′来确定可分配节点的圆弧并放置相应的子节点vn，径向树的时间复杂度为Ο(|v′|2+L|v′||vn|).由此可得，ERRTH算法的时间复杂度为Ο(k2+k|v′|)+Ο(|v′|2+L|v′||vn|).

4.2.2 实验指标分析 拥挤度[17]常被用于衡量集成电路布局设计是否合理的，拥挤度需要统计不同区域边缘的走线数Se和固定边缘走线数De，但在复杂网络中很难统计边缘走线数Se和De，因此不适用对复杂网络的布局结果进行评价.为对复杂网络的布局效果进行衡量，本文以区域内节点的数量来判定区域是否为拥挤区域，并提出拥挤区域占比来评价不同算法下的复杂网络布局效果.

定义5平均节点拥有量(avg_region).每个区域内拥有的平均节点数量，记为avg_region.

(8)

式中，num(v)表示节点总数；region表示区域总数；s和t表示布局图被划分出的行、列数.

定义6拥挤区域(crowd_area).若划分进某区域内的节点数量高于平均节点拥有量，则此区域被认定拥挤区域，记为crowd_area.

定义7拥挤区域占比(crowd_area_rate).拥挤区域的数量占所有区域的比例，记为crowd_area_rate.

(9)

如图9所示，给区域分配节点时，部分节点位于区域的边缘上，为将这部分节点划分至指定区域，本文提出一个“左部优先，上部优先”的节点划分策略. 节点1位于B，C两个区域，按照“左部优先”原则，节点1划分进了B区域.同样，节点3因“上部优先”原则被划分进E区域.但少数特殊节点如节点2，它位于区域A、B、D、E的边缘交叉处，按照划分策略，它会被划分进区域A.循环处理边缘节点至每个节点都被分配到相应区域，并依据式(9)计算出拥挤区域占比.拥挤区域占比越高，说明复杂网络的部分区域相对较拥挤，节点过于密集，不利于用户观察复杂网络.

图9 区域节点划分策略Fig.9 Regional node partitioning strategy

图10 不同算法的拥挤区域统计图Fig.10 Crowed area statistics of different algorithms

实验中的指标数据均采用python语言编程获得，实验结果分别如表1和表2所示.

由表1和表2的实验结果，以及图10分析得出，在相同的数据集下，采用径向树的ERRTH算法产生的拥挤区域明显少于其他布局算法，说明ERRTH算法可以有效减少复杂网络中的拥挤区域.再从点分布方差来看，ERRTH算法布局后的节点分布更为合理，可以降低节点拥挤导致的布局混乱和区域内节点的密集程度.

ERRTH算法的边长偏差和节点分布偏差低于其他布局算法，说明ERRTH算法相较于其他算法社区内的节点布局偏差较少，节点分布结果更均匀，更符合复杂网络布局的美学标.ERRTH算法为达到明确社区内节点层次结构的目的而采用径向树进行二次布局，这部分占用时间过多导致ERRTH算法的时间略高于其他算法，但算法之间差距不大，并且尚在用户可容忍时间范围2～8 s之内.

表1 Dolphins网络的实验结果

表2 Football网络的实验结果

此外，本文还采用ERRTH算法对线虫的神经网络(299个节点，2 359条边，数据集来源于Newman教授的个人网站)进行布局，运行时间稳定在16 s左右，拥挤区域的占比为0.4，远低于其他布局算法.可以推出ERRTH算法尤其适用于500个以下节点的布局，布局后的拥挤区域较少，节点分布较为合理.

最终从布局分析和算法效率分析的结果来看，ERRTH算法可以显著地分离两个社区，且高效地展示各个社区内网络层次结构，提高复杂网络社区结构的辨识度，对于网络布局较之传统布局有着较强可读性和可解释性，具有很强的使用价值.本文基于FR算法，提出嵌入社区半径的社区斥力和引力来分离复杂网络的社区，接着又采用径向树来排列各个社区内节点位置.前者可以避免各社区的聚拢和重叠，后者可以直观展示各个社区内层次结构，便于用户理解社区内节点之间的层次关系.与力引导算法和聚类布局算法相比，ERRTH算法可避免力引导算法不能分离社区以及现有的聚类布局算法不能显示社区内部节点结构关系的缺陷.

在对复杂网络进行社区划分时，网络中可能会存在一些同时与几个社区有联系，但又不属于任何社区的节点，它常位于社区的边缘区域被称为边缘节点.由于本文采用Kmeans算法来划分社区，该方法不能准确识别边缘节点和需要先给出聚类数目m.因此，在下一步工作中，将选用能识别边缘节点的社区划分算法来替代Kmeans算法，同时将本文布局算法运用到时变复杂网络[18]分析上去，使时变网络在布局时能保持网络结构和心智图[19]的稳定.