PTA干燥机搅拌系统有限元分析方法研究
2020-01-10王晓静张照汶王锡尧
王晓静,张照汶,王锡尧,刘 瑞
PTA干燥机搅拌系统有限元分析方法研究
王晓静,张照汶,王锡尧,刘 瑞
(天津大学化工学院,天津 300350)
针对某新型卧式回转PTA(精对苯二甲酸)干燥机的搅拌系统出现的断裂问题,提出一种新的有限元分析方法,即时间节点法,在搅拌系统一个转动周期内均匀地取多个时间点,对每一个时间点下的搅拌系统进行静力学分析模拟,然后将模拟得到的结果进行统计分析,绘制出变化曲线,描绘搅拌系统在转动过程中的变化过程.利用ANASYS workbench软件对时间节点法进行验证并对搅拌系统进行研究.研究结果表明,取8个时间节点来描述搅拌系统在一个周期内的变化过程最为合理,搅拌系统运转过程中在空心轴与实心轴交接部位出现最大应力,其值为118.56MPa,在螺带的最前端出现最大形变,其值为16.035mm,当料柱质量为12t时,疲劳寿命为3.54a,模拟分析得到的疲劳寿命与搅拌系统发生断裂的时间偏差为5.93%,且模拟结果中出现疲劳断裂的位置与搅拌系统发生断裂的位置相同,由此验证了时间节点法的准确性.研究内容为动设备的受力分析提供了新的方法和思路.
PTA干燥机;搅拌系统;有限元分析;时间节点法;疲劳寿命
工业生产中,PTA干燥机多为卧式回转干燥机,是一种以传导传热方式使物料加热、水分汽化的加热 器[1-3].与其他类型的干燥机相比,卧式回转干燥机有其显著的优点,在处理物料方面较其他类型的干燥器具有更大的灵活性;物料在筒体内充分混合且具有较长的停留时间;生产出的产品质量一致性较高;适合对干燥要求较高的产品进行干燥[4].卧式回转干燥机的核心部件是搅拌系统,搅拌系统被转动装置带动,对物料起到搅拌和推料的作用.由于搅拌系统多为悬臂结构,在实际运转过程中,经常会发生断裂破损问题.因此对卧式回转干燥机中搅拌系统的强度、刚度以及疲劳寿命的分析研究有着重大的意义[5-7].
搅拌系统在连续运转过程中,受到料液作用的部位不断变化,而静力学分析中无法设置受力位置不断变化的边界条件.因此采用某种方法实现静力学分析搅拌系统动态变化过程是分析搅拌系统断裂问题的关键[8-10].本文针对某新型PTA干燥机搅拌系统出现的断裂问题,提出一种新的有限元分析方法,利用ANASYS workbench软件对该方法进行准确性验证,并对干燥系统的强度、刚度和疲劳寿命进行校核,找到搅拌系统出现断裂的原因.
1 干燥机搅拌系统介绍
本文研究的卧式回转PTA干燥机的搅拌系统由搅拌轴、辐杆和螺带构成,结构模型如图1所示.

图1 搅拌系统结构模型
装有辐杆部分的轴为空心轴,连接电机且未安装辐杆部分的轴为实心轴.搅拌系统运行过程中物料从上方落下,对转轴形成一定的料柱压力,随后料液在搅拌系统的带动下在滚筒的下端向前流动.料液与底部螺带接触,对螺带产生一个反向的推力,随着搅拌轴的连续转动,与料液接触的螺带位置不断变化,致使料液对搅拌系统整体的作用力不断变化,设备参数见表1.
表1 设备参数

Tab.1 Device parameters
搅拌系统具有非对称性,在连续转动过程中一些部件的受力状态发生变化.而静力学分析中无法设置受力位置不断变化的边界条件,因此需要找到一种新的方法利用静态分析来完成动态分析,进而完成对PTA干燥机搅拌系统的有限元分析.本文提出一种新的有限元分析方法,即时间节点法,在一个运动周期内的各个阶段的受力状态都有差异,利用微积分的思想,将设备在一个周期内的连续转动过程看作是多个非连续转动的累积.即在设备的一个运动周期内均匀的取多个时间点,设备在运动到每一个时间点时均对其进行静力学分析.然后将各个时间点下分析得到的结果进行统计,绘制出变化曲线,当所取时间点到达一定数量时,结果则接近设备的真实状况.通过对模型在一个运动周期内多个时间点下的分析模拟,找到时间点合适的选取数量,得到搅拌系统在转动过程中所受的最大应力、变形和疲劳寿命.
2 搅拌系统应力和变形计算分析
2.1 建模与施加载荷

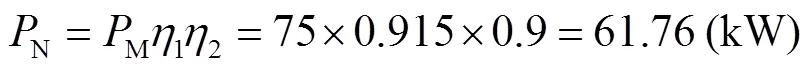
取轴摩擦损失3%,故取搅拌轴功率60kW.搅拌轴所受扭矩为

式中:e为搅拌系统所受扭矩,N·m;为搅拌功率,kW;为搅拌系统转速,r/min.
由于实际工作中只有螺带推料受到物料的反作用力,因此将扭矩等效为面载荷加载在螺带上,经计算加载轴正向力16377N,推料与几部分螺带同 时接触,因此需要将总作用力均匀加载到每个螺带上[13].加载情况如图2所示.
由于搅拌系统是连续转动的,图2仅表示搅拌系统开始转动时初始状态下的受力状态,当搅拌系统随转轴转动到一定角度时,与物料接触的螺带位置发生变化,因此,不改变坐标系方向,将模型转动一定角度,重新对模型进行加载.图3为搅拌系统分别转动90°和180°后的载荷加载,由图3可知,随着搅拌系统的转动,与物料接触的螺带位置发生明显变化,因此,重新加载时料柱压力大小、方向不变,而料液对螺带的反作用力加载在此时刻与料液接触的螺带上,此种加载方式符合生产过程中搅拌系统的真实受力情况.通过转动模型多次加载的方式对搅拌系统转动一周内的多个时间点下不同受力状态分别进行有限元分析,得到搅拌系统转动过程中各个时况下的受力和变形情况,并绘制出变化曲线,而本文所研究的时间节点法也正是以这种特殊的加载方式为基础提出的.

C—轴端固支;D—轴承支撑

图3 搅拌系统在转动不同角度时载荷加载
2.2 搅拌系统应力和变形计算分析
分析过程中发现在实心轴与空心轴交接部位和辐杆的根部均可能出现最大应力,因此分别对两处在一个转动周期内所受应力进行分析.
2.2.1 辐杆根部应力分析
在搅拌系统一个转动周期(即转动360°)内分别取4个时间节点(每转动90°取一个点)、8个时间节点(每转动45°取一个点)和16个时间节点(每转动22.5°取一个点),对每个时间节点下的模型进行重新加载并分析得到该时刻下辐杆根部的应力值,绘制出应力随搅拌系统转动的应力变化曲线,如图4所示.
由图4可知,辐杆根部应力随着搅拌系统的转动发生变化,这是由于整体结构的非对称性导致的.取4个和8个时间节点时得到的应力变化曲线有明显的差异,说明仅取4个时间节点对应力变化去曲线进行描绘是不符合实际的,节点选取越多应力变化曲线更加接近真实的应力变化过程,继续增加时间节点至16个,此时的应力变化曲线与取8个节点时基本相同.从图中可以看出在转动到75°时辐杆根部出现最大应力为118.56MPa,出现最大应力时搅拌系统的受力云图如图5所示.


图5 辐杆根部出现最大应力时搅拌系统的受力云图
2.2.2 空心轴与实心轴交接部位应力分析
分别取4、8、16个时间节点时空心轴与实心轴交接部位应力随搅拌系统转动变化曲线如图6所示.由图6可知,取不同个数时间节点时得到的应力变化曲线基本相同,结合第2.2.1节得到的规律,在取8个时间节点时得到的应力变化曲线基本可以表达出此部位的受力状态变化过程和应力极值,在转动到67.5°时辐杆出现最大应力为114MPa,出现最大应力时搅拌系统的受力云图如图7所示.

2.2.3 搅拌系统总变形分析
分别取4、8、16个时间节点时搅拌系统最大变形随搅拌系统转动变化曲线如图8所示.由图8可知,取4个时间节点无法完整描绘最大形变随转动变化曲线,随着时间节点选取数量增加到8个,最大变形随转动变化曲线逐渐完善,时间节点增加到16个时,得到的变化曲线与取8个时间节点时基本一致,由此说明在时间节点为8个时基本可以表达出分析目标的变化过程和极值.当搅拌系统转动到90°时出现最大变形16.035mm,出现位置为轴端,出现最大变形时搅拌系统的变形云图如图9所示.

图7 空心轴与实心轴交接处出现最大应力时搅拌系统的受力云图

综上所述,通过时间节点法对搅拌系统进行有限元分析,得到搅拌系统在转动到75°时在辐杆处出现最大应力为118.56MPa,搅拌系统转动到90°时在轴端出现最大变形为16.035mm.对于时间节点法,取8个时间节点绘制的受力状态和变形变化曲线对PTA干燥机搅拌系统的描述最合理,节点过少不能反映真实变化情况,节点过多增加工作量.

图9 搅拌系统出现最大变形时的变形云图
3 搅拌系统疲劳分析
由上文可知搅拌系统转动过程中所受最大应力为118.56MPa,搅拌系统所用材料304L不锈钢在小于150℃时的许用应力为137MPa,因此整个搅拌系统满足强度要求.实际生产过程中搅拌系统也并未发生直接的断裂,而是在使用了一段时间后发生断裂,而搅拌系统运转过程中,由于转轴的转动,转轴受到从上而下的物料反复的冲击,进而对转轴造成疲劳破坏,由此考虑断裂的原因为疲劳断裂,因此需要对搅拌系统进行疲劳寿命分析.
利用时间节点法找到物料冲击部位(危险截面)的最大拉压应力,进而计算搅拌系统的疲劳寿命.根据上文所得结论,选取8个时间节点,分别分析搅拌系统转动到不同时间节点时危险截面处的轴向应力,绘制危险截面轴向应力随搅拌系统转动的变化曲线,如图10所示.
从图10中可以看出,当搅拌系统转动90°时,截面下端出现最大压应力66.01MPa,在搅拌系统转动到270°时,截面上端出现最大拉应力32.9MPa,最大拉压应力出现时间相差半个转动周期,即最大拉压应力出现在同一个位置,故该位置在转动过程中所受应力幅值最大为98.91MPa.因此当该位置转动到转轴的上端和下端时,相比转轴其他位置更容易发生疲劳破坏,由此可将动态疲劳问题转换成该时间节点下反复受力的静态疲劳问题,分析此种状态下搅拌系统的疲劳寿命.搅拌系统运转过程中,每转动一个周期,预分析的疲劳点分别受一次拉力和一次压力,修改疲劳参数,得到疲劳寿命云图,如图11所示.

图10 危险截面轴向应力随搅拌系统转动变化曲线

图11 搅拌系统寿命云图
搅拌系统转速为33.8r/min,每日工作24h,全年工作330d,计算得到搅拌系统每年的实际转动次数为1.6×107.从图11可以看出,当转轴受到12t料柱压力时,转轴危险截面的最低转动次数为5.67×107,空心轴边缘处疲劳寿命过低的原因是模型未建立倒角,此处发生应力集中,实际此处并未发生断裂,且有焊缝加强.因此只分析危险界面处的疲劳寿命.根据分析得到的结果,搅拌系统的工作寿命为3.54a,而后发生断裂.改变加料量,得到料柱质量与搅拌系统工作寿命的关系,如表2所示.
表2 搅拌系统工作寿命与料柱质量的关系

Tab.2 Relationship between the working life of the stir-ring system and the mass of the column
由表2可以看出当料柱质量为11.5t时,搅拌系统工作寿命为25.6 a,满足设计要求,而继续增加物料量会使其工作寿命明显降低,不能达到设计要求.因此可以在生产工艺上进行改进,解决搅拌系统出现的断裂问题.
4 实例验证
卧式回转PTA干燥机的搅拌系统,材料为304L不锈钢,工作温度不高于150℃,该搅拌系统设计的工作寿命为20a,而实际运转过程中,在设备运转3.33a后搅拌系统中的转轴出现断裂,位置在空心轴和实心轴交接处,干燥机内部介质为含醋酸的滤饼,不含硫元素,因此不存在酸浸腐蚀问题.通过本文对搅拌系统转动过程的分析表明,转轴上出现最大应力的位置与搅拌系统在转动过程中发生断裂的位置一致,如图12所示.

图12 转轴断裂位置与模拟分析出现最大应力位置对比
由于搅拌系统的非对称性,物料的冲击会导致转轴发生疲劳破损,而转轴出现最大应力位置也是最容易发生疲劳破损的位置.因此,本文对转轴断裂位置进行了疲劳寿命分析,模拟分析得到搅拌系统的工作寿命为3.54a,与转轴出现断裂的时间相比,模拟分析得到的断裂时间与实际发生断裂的时间偏差为5.93%,由此说明模拟分析得到的断裂位置与断裂时间均与实际情况相一致,验证了本文提出的模拟方法的正确性.
5 结 语
通过对PTA干燥机搅拌系统的有限元静力学分析,验证了笔者提出的时间节点法的准确性. 找到此方法下可以描绘出搅拌系统真实受力情况的最低时间节点个数,结果表明,取8个时间节点来描述搅拌系统在一个周期内的变化过程最为合理. 利用时间节点法分析搅拌系统的强度、刚度和疲劳寿命,结果表明,搅拌系统在转动过程中的强度和刚度均满足要求,分析计算得出搅拌系统的疲劳寿命为3.54 a,疲劳断裂的位置与搅拌系统发生断裂的位置相同,由此说明搅拌系统出现断裂的原因为疲劳断裂,并针对搅拌系统出现的疲劳断裂问题给出合理的改进意见.
[1] 王艳艳,王团结,彭 敏. 常用干燥设备的应用及其选用原则研究[J]. 机电信息,2017(2):1-16.
Wang Yanyan,Wang Tuanjie,Peng Min. Application of common drying equipment and its selection principles[J]. Mechanical and Electronic Information,2017(2):1-16(in Chinese).
[2] 万风岭,谢苏江,周昭军. 干燥设备的现状及发展趋势[J]. 化工装备技术,2006(1):10-12.
Wan Fengling,Xie Sujiang,Zhou Zhaojun. The current situation and development trend of drying equipment [J]. Chemical Equipment Technology,2006 (1):10-12(in Chinese).
[3] 倪春林,史元芝,马训强,等. 适合高湿、高黏物料的干燥设备的研究与应用[J]. 山东化工,2009,38(8):32-35.
Ni Chunlin,Shi Yuanzhi,Ma Xunqiang,et al. Study and development of drying system for waterish and sticky material[J]. Shandong Chemical Industry,2009,38(8):32-35(in Chinese).
[4] 张素梅. 回转式圆筒干燥机设计[J]. 科技创新与应用,2015(28):45-45.
Zhang Sumei. Design of rotary cylinder dryer[J]. Science and Technology Innovation and Application,2015(28):45-45(in Chinese).
[5] 杨连红,王 强,赵胜强. 基于ANSYS的PTA干燥机的有限元分析[J]. 石油和化工设备,2016,19(4):5-8.
Yang Lianhong,Wang Qiang,Zhao Shengqiang. Finite element analysis of PTA dryer based on ANSYS[J]. Petro-Chemical Equipment,2016,19(4):5-8(in Chinese).
[6] 祝明威,冯武文,习进朝. 某回转圆筒式干燥机的整体有限元分析[J]. 农机化研究,2007(12):64-67.
Zhu Mingwei,Feng Wuwen,Xi Jinchao. Finite element analysis on one kind of rotary dryer[J]. Journal of Agricultural Mechanization Research,2007(12):64-67(in Chinese).
[7] 刘 旺,郎 勇,李春宝. PTA干燥机进料机螺旋轴断裂原因分析及修复[J]. 化工设备与管道,2018(2):54-55.
Liu Wang,Lang Yong,Li Chunbao. Cause analysis and repair of fracture occurred in rotary shaft in feeding component in PTA dryer[J]. Process Equipment & Piping,2018(2):54-55(in Chinese).
[8] 余伟炜,高炳军. ANSYS在机械与化工装备中的应用[M]. 北京:中国水利水电出版社,2006.
Yu Weiwei,Gao Bingjun. Application of ANSYS in Mechanical and Chemical Equipment[M]. Beijing:China Water & Power Press,2006(in Chinese).
[9] 余联庆,梅顺齐,杜利珍,等. ANSYS在结构优化设计中的应用[J]. 中国水运:理论版,2007,5(3):78-79.
Yu Lianqing,Mei Shunqi,Du Lizhen,et al. Application of ANSYS in structural optimization design[J]. China Water Transport:Theoretical Edition,2007,5(3):78-79(in Chinese).
[10] Elksnin V,Priimak O. Application of mathematical modeling using super components for designing chemical and oil and gas equipment[J]. Chemical & Petroleum Engineering,2011,47(5/6):342-350.
[11] 李冬慧. 多晶硅固渣卧式干燥机搅拌系统力学分析及结构优化[D]. 天津:天津大学,2012.
Li Donghui. The Mechanical Analysis and Optimal Design of the Mixing Sstem in Horizontal Dryer[D]. Tianjin:Tianjin University,2012(in Chinese).
[12] 王晓静,马东云. 异型热管反应器硅烷分解过程流场的数值模拟[J]. 天津大学学报:自然科学与工程技术版,2018,51(3):278-283. Wang Xiaojing,Ma Dongyun. Numerical simulation of flow field in silane decomposition process of reactor with shaped heat pipes[J]. Journal of Tianjin University:Science and Technology,2018,51(3):278-283(in Chinese).
[13] 黄益平,马东云,王晓静,等. 连续式干燥机搅拌系统力学分析及优化[J]. 石油化工设备,2016(6):32-37.
Huang Yiping,Ma Dongyun,Wang Xiaojing,et al. Development and mechanical analysis of continuous dryer for poly silicon slurry disposition[J]. Petro-Chemical Equipment,2016(6):32-37(in Chinese).
Finite Element Analysis Method for PTA Dryer Stirring System
Wang Xiaojing,Zhang Zhaowen,Wang Xiyao,Liu Rui
(School of Chemical Engineering and Technology,Tianjin University,Tianjin 300350,China)
In this paper, we proposed a new finite element analysis method, the time-node method, for analyzing fracture problems in the stirring system of a new type horizontal rotary PTA (fine terephthalic acid) dryer. We systematically obtained a plurality of time points in one rotation cycle and performed a static analysis of the stirring system at each time point. We then drew stress and deformation curves to characterize the rotation cycle of the stirring system. We used the ANASYS workbench environment to verify the performance of the time-node method. The results indicate that it is most reasonable to take eight time points to describe the stress and deformation variations of the stirring system in one rotation cycle. During the operation of the stirring system, a maximum stress of 118.56 MPa occurs at the junction of the hollow and solid shafts and a maximum deformation of 16.035 mm occurs at the forefront of the ribbon. We obtained a simulated fatigue life of the stirring system of 3.54 years when the mass of the column is 12 t, which is a deviation of just 5.93% from the actual project case. The location of the simulated fatigue fracture also matches quite well with the actual case, thus verifying the accuracy of the time-node method. The results presented in this paper provide a new method and references for stress and fatigue analysis of dynamic equipment.
PTA dryer;stirring system;finite element analysis;time node method;fatigue life
TK173
A
0493-2137(2020)02-0214-07
10.11784/tdxbz201901023
2019-01-11;
2019-04-08.
王晓静(1965— ),男,博士,副教授.
王晓静,tdxjwang@126.com.
(责任编辑:田 军)
