空间飞网捕获过程动力学研究
2020-01-10武彦伟高怀亮
沈 剑,武彦伟,高怀亮
(1.中北大学 机电工程学院, 太原 030051; 2.晋西集团山西江阳化工有限公司, 太原 030041;3.重庆长安工业集团有限责任公司, 重庆 401120)
根据美国宇航局(NASA)的数据,超过50万的碎片围绕地球运行,但技术上的限制使得只有大约2万个碎片可以被跟踪。它们以每秒约7 800 m的速度飞行,并对人类太空活动构成严重威胁[1]。有关于太空垃圾清除的分析研究和工程新方法有很多类,例如美国航天局的TSS-1R任务[2]。国外关于空间飞网的研究主要集中在空间飞网捕捉以及绳索动力学两个方面[3]。空间飞网是由多个物理节点连接横纵双向多条绳索(带)组成的,结构轻盈、易折叠、收缩比例大[4]。在绳网动力学研究方面,国内外的研究主要还是采用集中质量法等简化模型,如果要精确地模拟空间飞网的运动过程和构型变化,则需要采用多体系统动力学方法来进行绳网柔性体建模,例如绝对节点坐标法(ANCF)[5]。
不同于集中质量模型,ANCF离散的是柔性体,并且单元的应变模型是影响仿真精度的主要物理因素[6]。M.Berzeri和A.A.Shabana提出的纵向和横向双向弹性力计算模型[7],根据是否假设纵向变形为小变形来选择不同的计算模型。但对于单元尺寸或迭代步长较大时,采用这种模型计算就会发散。Wago T等人对文献[7]中的单元应变模型进行了改进,建立了柔性索单元准确、合适的刚度矩阵,可更真实地描述柔性体的变形过程[8]。张越等针对传统绝对节点坐标方法(ANCF)绳索模型,考虑纤维绳索初始松弛余量,推导了松弛绳索动力学模型,通过仿真验证了松弛模型能够更好地反映绳索在松弛状态下的动力学特性[9]。
本文基于ANCF法建立柔性索单元模型,针对轴向应变模型影响计算精度的问题,采用基于弧长积分的轴向应变模型来进行计算。通过仿真分析研究空间飞网在捕获太空目标过程中的动力学特性。
1 空间飞网动力学模型
1.1 ANCF索单元
Gerstmayr J和Shabana A A于2006年在文献[5]中提出了一种低阶的索单元,该单元是基于连续介质理论,从Euler-Bernoulli梁单元演变而来,通过Green应变描述单元位移、转动、应变等物理特性。对于柔性绳索,可考虑绳索轴向和弯曲应变,忽略剪切应变,适合于空间柔性绳网这种大变形、非线性的动力学模型建模需要。单元的假设为各向同性,只受拉力作用不受压,并且不考虑剪切、扭转变形。
索单元属于一维二节点单元,如图1所示。在三维建模中,每个节点坐标由位置矢量和该点的位置梯度矢量组成,共6个坐标,每个单元含有12个坐标。节点i坐标为:
ei=[e1,e2,e3,e4,e5,e6]=
(1)


图1 一维二节点索单元示意图
单元坐标可以表示为:
e=[ei,ej]T
(2)
索单元被认为各向同性,因此其与纵向拉伸变形相关的应变能可以表示为[10]:
(3)
式(3)中,εl代表纵向拉伸应变,下标l代表纵向Longitudinal的英文首字母;E代表单元弹性模量;A代表单元横截面积。
纵向拉伸应变εl及变形后长度ls表达式为:
(4)
与纵向拉伸变形相关的弹性力表达式为:

(5)
相应刚度矩阵表达式:
(6)
类似地,与弯曲变形相关的应变能可以表示为:

(7)
式(7)中,κ代表当前构型单元圆弧的曲率,下标t代表横向Transverse的英文首字母;E代表单元弹性模量;I代表单元截面惯性矩。
在建模中,假设索单元纵向变形为小变形,则曲率的表达式为:

(8)
式(8)中,双下标xx代表单元上任一点的位置矢量r对物质坐标x的二阶导数。
与弯曲变形相关的弹性力表达式为:
(9)
相应刚度矩阵表达式:
(10)
单元总刚度矩阵:
K=Kl+Kt=
(11)
1.2 动力学方程及数值算法
根据第一类拉格朗日方程,建立空间飞网的运动方程为:

(12)
式(12)中,C(e,t)表示约束方程。
将运动方程表示为矩阵形式,有:

(13)
式(13)中,λ为拉格朗日乘子;Ce为约束方程雅克比矩阵;R为约束方程对自变量的二阶偏导数。
方程式(13)属于微分-代数方程(DAE)。对于求解长时间历程的DAE方程,传统算法不稳定,容易产生数值耗散[11]。对此,Bathe[12-14]提出了一种适用于长时间历程非线性问题的求解方法,后来Tian Q等[15]对Bathe法应用于DAE方程求解的策略。方程式(13)系数矩阵是非对称的稀疏矩阵,属于大型非对称稀疏矩阵问题,可采用 GMRES 方法求解[16]。为减小内存占用,提高调用效率,本文采用Bathe积分策略和Matlab内置函数gmres联合的方法进行方程式(13)的求解。
2 轴向应变模型和捕获碰撞模型
在空间飞网动力学仿真的过程中,计算的收敛能力与迭代步长和单元结构尺寸之间有着密切的关系。当这两方面因素满足要求且计算能够收敛后,单元的应变曲线和节点的速度曲线等仍然存在高频振动,计算精度偏低。带来这种计算低精度的原因主要与单元的轴向应变模型有关[17]。空间飞网的实时构型求解对于目标捕获任务的顺利完成有很大影响。
2.1 基于弧长积分的轴向应变模型
文献[7]中建立了ANCF的索单元轴向应变模型L1。如图2所示,假设单元原长l,变形后纵向长度为ls,模型L1计算得到纵向长度为lL1。对于图2中示例1的情况,发生弯曲变形的单元实际轴向长度ls大于原长l,而利用模型L1计算出来的两节点间直线长度lL1却小于原长,与事实不符;当发生示例2的情况时,实际的轴向长度大于原长,而模型L1计算出来的数值却等于原长。当单元变形后其轴向长度大于原长(即纵向应变大于零)时,L1模型所计算出的轴向应变不能反映真实情况,导致单元弹性力计算为零甚至为负情况出现[8]。文献[8]中提出一种基于绝对节点坐标公式的三维Bernoulli-Euler梁单元轴向弹性力的改进形式。针对柔性梁弯曲变形较大的算例,将传统的轴向弹性力计算公式(例如上述L1模型)与文献[8]中的计算公式进行了比较。对比结果表明,该公式可以用较少单元精确地表达梁单元的大变形。因此,针对空间飞网运动过程中的大变形动力学特性,可以采用该公式计算单元的轴向应变。
假设变形后单元轴向长度为ls,可以沿着索单元中心线对微元弧长进行积分得到:
(14)
微元的弧长可以表示成单元位置梯度矢量的函数,即:
(15)
式(15)中,下标x代表单元上任一点的位置矢量r对物质坐标x的导数,即单元位置梯度矢量:

(16)

(17)

(18)
略去高阶项,只取前两项,并代入式(17)可得:


(19)
将式(19)代入式(4)就可以更精确地计算索单元纵向拉伸应变,进而计算相应弹性力和刚度矩阵。

图2 文献[7]中的L1模型
2.2 捕获碰撞模型
在空间飞网捕获目标时,需要进行飞网与目标的碰撞检测。采用文献[18]的绳网捕获碰撞模型,对飞网上的节点与刚体进行实时碰撞检测,可以模拟出飞网在接触、碰撞目标后的空间构型变化过程。仿真中实时判断绳网节点与目标中心的距离,接触后需考虑绳索与目标的接触力。
2.2.1碰撞检测
将目标构型简化为半径为R的球体。首先通过判断检测点和刚体的空间位置对两者进行检测,如果检测到运动体相互之间存在侵入,则计算目标刚体对绳索的侵入量,进而根据绳索与目标间的接触模型计算接触碰撞力,并更新运动体的状态。 假设球体中心坐标为(x0,y0,z0),绳网节点(xi,yi,zi)是否与目标球体接触的判据为:
(20)
当Δr=R时节点与球面开始接触。
碰撞的法线方向为:

(21)
碰撞侵入量为:
(22)
2.2.2碰撞力计算
假设碰撞接触力为F,转化为广义形式为:
Q=STF
(23)
将绳网与目标之间的碰撞过程可以等效为非线性弹簧阻尼模型。其中,碰撞处的恢复力由Herz接触理论中弹簧接触力描述,能量损失由阻尼器模拟。碰撞体受到的弹簧接触力的方向与它们在碰撞处相互穿透的方向相反,并且承受的都是压力,受到的阻尼力的方向为它们相对运动速度的反方向[18]。根据Hertz理论,法向接触力的大小为:

(24)
式(24)中,K等效接触刚度;C等效接触阻尼。
3 仿真分析
3.1 材料参数
空间飞网大多采用柔性材料编织而成,例如高强度尼龙织带等。仿真中所用到的材料参数如表1所示。

表1 索单元材料参数
3.2 空间飞网自由悬挂下落仿真
以网体一端固定一端自由下落为算例,通过仿真分析,绳网在不同时刻的空间构型差异如图3所示。

图3 不同时刻下空间飞网构型示意图
图4表示绳网末端单元的轴向应变变化情况。在重力作用下悬垂下落,末端单元轴向变形最大,在t=3.852 s时刻轴向应变达到了0.115 7。图5所示为绳网末端单元的节点Y向位移曲线,可知呈周期性变化。随着能量的衰减,最终趋于0附近。

图4 绳网末端单元轴向应变曲线

图5 绳网末端单元节点Y向位移曲线
3.3 空间飞网捕获动力学仿真
为了验证本文建立的空间飞网模型、轴向应变模型和捕获碰撞模型,对空间飞网捕获太空目标的过程进行仿真分析。仿真过程中不考虑重力作用。飞网材料参数如表1所示,其余模型参数如表2所示。
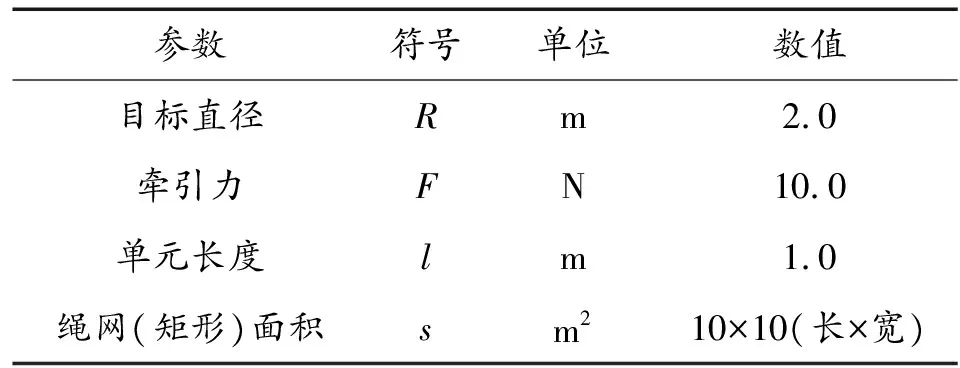
表2 空间飞网捕获模型参数
牵引力施加于网体四个角点,沿Z向正向为正。空间飞网捕获太空目标过程如图6所示。
由图6可以看出,t=0.2 s时网体接触目标后开始变形,并开始包覆目标;t=0.3 s时,目标体一半的表面被网体覆盖;t=0.4 s时,网体覆盖目标面积超过4/5,可认为捕获成功。仿真中网体变形稳定,流线型效果较好,在一定程度上能够反映真实的空间飞网捕获过程中的姿态和构型变化。

图6 空间飞网捕获太空目标过程示意图
4 结论
1) 本文采用ANCF索单元建立空间柔性绳网模型,引入基于弧长积分的轴向应变模型精确计算单元轴向应变,结合绳网捕获碰撞模型,可以较好地模拟空间飞网捕获太空目标的过程。
2) 本文研究成果可用于工程中各类大变形柔性绳网的建模和仿真工作。
3) 计算发现,算法的高效性对于求解大规模网体的动力学方程组十分重要。未来需要对算法的收敛性、海量数据存储等问题进行深入研究。
