结合依存关系与同义词词林的相似度计算
2020-01-10付鹏斌陈帅帅杨惠荣李建君
付鹏斌,陈帅帅,杨惠荣,李建君
(北京工业大学 信息学部,北京 100124)
0 引 言
语义相似度是给定一组文本,评价这一组文本之间内容表达相似程度的量度[1]。语义相似度出自计算语言学领域,目前广泛应用于自然语言处理中的Web信息可信分析、搜索引擎、Web服务发现、文本聚类研究和标识释义等领域[2]。
在语义相似度的研究方法中,主要分为基于词向量的语义距离相似度计算方法和基于语法结构的语义相似度计算方法。其中,基于词向量的语义距离相似度计算,是将文本中的词频转化为词向量的形式,然后在词向量的基础上计算空间距离的长度,以此来表示文本的语义距离相似度。目前,主流的词向量转化方法是TF-IDF(term frequency-inverse document frequency)方法,TF-IDF方法是计算出文本中词的词频集合[3]。而使用TF-IDF方法将中文文本转化成词向量,比较不同词向量在线性空间中的相似度有余弦距离、欧氏距离、概率分布距离(K-L距离)等方法。文献[4]使用向量空间模型计算文本的语义相似度,使用TF-IDF算法将文本转化为词向量,然后将这些词向量映射到文本向量空间,这样就将一组文本之间的匹配问题转化为求向量空间的距离问题。但是,基于向量空间模型的语义相似度只是单纯地计算词向量之间的空间距离,没有考虑句子中词语的词序和句子的结构信息对句子语义的影响。文献[5]使用基于词性信息的改进TF-IDF算法去计算每个词向量之间的权重系数,然后将这些权重系数应用到向量空间和马尔可夫模型中,分别计算它们的语义相似度,最终获得整体的语义相似度。但是,文献[5]没有精确地反映出每个词向量之间的语义关联,如果在词向量中同时考虑到语义结构,那么该方法在文本语义相似度中有更好的表现。
在基于语法结构的语义相似度计算方法中,应用最广泛的语法结构是依存句法结构。依存句法是法国语言学家L. Tesnier[6]提出的,这种句法结构将句子的内部成分之间的依赖关系更加清楚地呈现到开发者的面前。语义依存关系能准确反映句子成分之间的搭配关系,李彬[7]利用句子的关键依存关系来匹配相似度,但是只使用依存关系中的词来计算依赖关系的相似性,不能准确地反映句子的内部语义关系。文献[8]对中文依存句法树进行研究和分析,提出一种细粒度依存关系的相似度计算方法,该方法基于依存句法树中的各节点的词语、词性以及它们之间的依赖关系及其重要性权重等多个特征值,给出了两个依存句法结构的相似度计算方法。但是,文献[8]计算复杂度特别大, 当文本的句长特别大时,消耗的时间较多,影响文本的语义相似度计算的效率。
而目前针对基于依存关系的语义相似度计算方法中,只考虑文本中词语的词序信息和句子的结构信息,而忽略文本中单个词语之间的词义信息。因此,文中在基于依存关系的语义相似度计算方法的基础上,增加了基于同义词词林的词语语义相似度计算方法,较好地解决上述问题,弥补以上不足。
1 相关技术
1.1 依存关系图
定义1:依存关系图Rs=(Vs,Es),Vs为图中所有顶点的集合,Es为图中所有相邻边的集合。且满足条件:∀e∈Es,∃u,v∈Vs(u≠v),使得e=(u,v)。
依存关系图是根据标注关系连接分词的,图中的每个顶点表示的是一个分词,子节点表示文本的依存词,父节点表示文本的中心词,子节点是依赖于父节点,它们直接使用连接弧来反映它们之间的依存关系。其中依存关系的标志类型有15种[9],如表1所示。

表1 依存句法分析标注关系
1.2 同义词词林
《同义词词林》[10]是以树状的形式将所有的词语编织在一起,将所有的词语可以分为大类、中类和小类这三类形式。为了更能细化各个词语之间的语义关系,《同义词词林》将小类又细分为词群和原子词群。词群是将小类中的词语根据词语之间的词义相关性和词义相似性进行划分,而原子词群又在词群的基础上进行划分,每个原子词群之间的词语相关性特别的接近而且词义相似性几乎相同。根据上述分析,可以将《同义词词林》分为5层树状结构,它们以编码的形式进行体现。第一层的编码形式使用英文大写字母表示;第二层的编码形式使用英文小写字母表示;第三层的编码形式使用两位阿拉伯数字表示;第四层使用英文大写字母表示;第五层使用两位阿拉伯数字表示。同时为了体现第五层的词义相关性和词义相似性,单独增加一位编码进行标记,标记有3种,分别是“=”、“#”、“@”,其中“=”代表“相等”、“同义”;“#”代表“不等”、“同类”,属于相关词语;“@”代表“自我封闭”、“独立”,它在词典中既没有同义词,也没有相关词。具体的编码描述如下:
<词义编码>=<大类><中类><小类><词群><原子词群><标记>
例如:编码“Ba01A02=”的词语类别为“物质 质 素”,它的编码描述见图1。

编码位12345678符合Ba01A02=符号类别大类中类小类词群原子词群标记层数第一层第二层第三层第四层第五层
图1 测试用例的编码描述
2 依存关系与同义词词林相结合的语义相似度计算方法
文献[11]提出一种基于句法依存分析的路径相似度计算方法,该方法首先对文本进行句法依存分析,获得依存树,然后在依存树中提取关系路径,最后进行路径间相似度的计算。
文献[12]提出并实现了一种基于同义词词林的词语相似度计算方法,该方法从词语的语义出发,根据词语的义项在同义词词林的位置和编码,计算出词语的相似度。
文献[11]只考虑文本中词语的词序信息和句子的结构信息,而忽略文本中单个词语之间的词义信息。而文献[12]只是从词语的语义出发,没有考虑文本的句子结构。因此文中提出了使用依存关系与同义词词林相结合的语义相似度计算方法,建立了一种结合依存关系与同义词词林的语义相似度模型,如图2所示。该模型以哈工大自然语言处理平台为基础,将文本A和文本B进行中文分词、词性标注、语法分析和语义分析等包装,最终获得依存关系图;在依存关系图的基础上提取关系路径;使用基于《同义词词林》的词汇语义相似度和基于搭配对的关系路径计算文本之间的语义相似度。
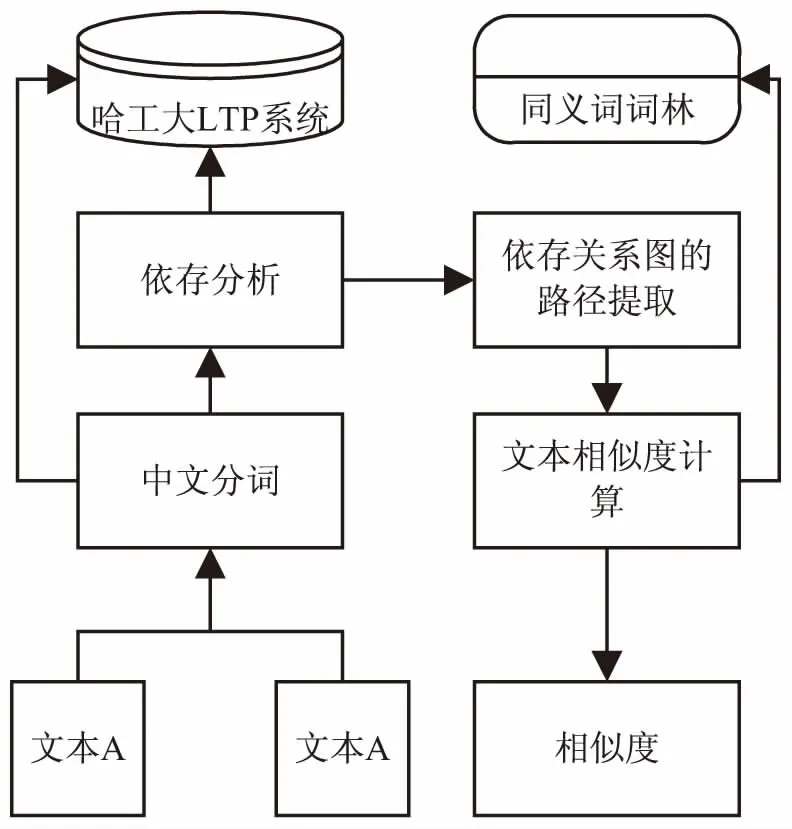
图2 依存关系与同义词词林相结合的语义相似度模型
2.1 依存关系图中的关系路径提取
定义2:关系路径p可以表示为从依存关系图的节点v0开始,到节点vn结束中间所经过的一系列边es⊆Es和顶点vs⊆Vs所构成的集合。且满足以下两个条件:
连接性:∀i:(vi-1,vi)∈Es∨(vi,vi-1)∈Es;
无环性:∀i∀j:i≠j→vi≠vj。
传统的计算文本之间语义相似度的方法是通过对词语之间的语义相似度进行加权求和,而文中在计算语义相似度时加入了依存句法结构,所以可以将计算文本之间的语义相似度转化为求关系路径间词语的加权之和。关系路径即通过遍历依存关系图,获得图中任意两个顶点之间的通路,并根据通路得到两个顶点之间的依存关系,它可以表示文本中词语之间直接或间接的关系。每一个依存关系表示一个直接的语义关系,而一条关系路径表示两个词语之间非直接的语义关系。因为关系路径是整个句子的一部分,所以可以通过不同文本间对应的关系路径的相似度来计算出文本间的相似度[13]。
通过下面的算法流程在依存关系图中提取关系路径[14]。
(1)算法输入:依存关系图Rs=(Vs,Es),Vs为图中所有顶点的集合,Es为图中所有相邻边的集合。且满足条件:∀e∈Es,∃u,v∈Vs(u≠v),使得e=(u,v);
(2)初始化顶点集合S为空集,初始化关系路径集合C为空集;
(3)∀x∈Vs,将x添加到S中;
(4)若(∃u∈S)∧(∃v∈Vs-S)满足(u,v)∈Es∨(v,u)∈Es,则将v添加到集合S中;
(5)寻找S中所有节点之间存在的路径P=
(6)若S≠Vs,转到3。否则,算法结束,返回关系路径集合C。
2.2 基于同义词词林的词语语义相似度计算
根据《同义词词林》的分析可得,若是两个词语的编码形式在第一层上有所区别,则说明两个词语不在同一个大类中,它们之间的词义几乎没有相关性,如果在第一层的编码相同,说明它们之间的词义具有相似性,具体的相似性大小可以根据下方的算法流程进行计算。文中采用的算法定义是:在树形结构中,两个词语的语义相似性与它们所处的层级成反比,对于标记位进行特殊处理[15]。具体的词语语义相似度计算方法如下方的算法流程所示:
(1)算法输入:两个词语S1和S2;
(2)查询同义词词林,分别获得词语S1和S2的编码形式code1和code2;
(3)遍历code1和code2,如果code1和code2的编码形式都相同,则SenseSim(S1,S2)=1,同时返回到第5步,反之,到第3步;
(4)如果code1和code2的编码形式除标记位相同,若标记位等于“=”符号或“@”符号,则SenseSim(S1,S2)=1,否则,SenseSim(S1,S2)=0.5,同时返回到第5步,反之,到第4步;
(5)如果code1和code2的编码形式的前i-1位编码都相同,而第i位编码不同,确定i在同义词词林树状结构中的层数j(其中层数j的获得在1.2小节中有介绍),则SenseSim(S1,S2)=1/(12-(2*j));
(6)返回词语语义相似度SenseSim(S1,S2)。
2.3 关系路径间语义相似度计算
通常情况下,计算文本的语义相似度是通过计算词语之间的语义相似度的加权求和。类似地,计算路径间语义相似度,可以将2.1小节中提取的关系路径转化为计算词语语义相似度计算的方法,但是这种计算方法不能完全体现词语之间的无歧义性的依存关系,以及词语之间的直接或间接依存关系[16]。因此,可以使用式1表示关系路径pi:
pi=<
(1)
其中,wi为关系路径pi上的一个顶点;ri为指向顶点wi的有向边的依存关系。
则两条关系路径Pi和Pj的语义相似度可以用式2计算得到。
S(Pi,Pj)=
(2)
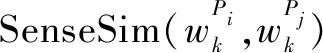

表2 依存关系的权重
2.4 结合依存关系与同义词词林的语义相似度计算

设文本A的关系路径集合中最大的一条关系路径的长度为max_path_count_A,文本B的关系路径集合中最大的一条关系路径的长度为max_path_count_B,设length(p)为关系路径p(p∈ΠA∪p∈ΠB)的长度,且0 其中关系路径集合T1和T2满足下面的规则: 关系路径集合T1和T2中的关系路径一一对应,构建x*y维的相似度矩阵MAB(i),具体的计算方法[18]如下: (3) (2)使用式4计算关系路径集合T1和T2的语义相似度Xwss(i),Xwss(i)具体表示关系路径长度i在关系路径集合T1、T2上的语义相似度,具体计算过程如下: (4) (3)Xwss(AB)表示文本A和文本B之间的加权语义相似度,具体的计算过程如下: (5) (4)计算所得的Xwss(AB),就是文中所求的文本语义相似度。 采用陕西省某重点中学2019届高二年级共1 038名学生的第二学期历史期末考试试题作为实验数据集,一共采集了2 076条文本数据,每条文本数据包括学生答案、教师给分、该试题总分,及该题的标准答案。从实验数据集中选取典型的236条数据作为实验数据,使用文中基于改进的依存关系的文本相似度算法,以及胡宝顺[11]和田久乐[12]提出的相似度方法分别在实验数据上计算相似度,最后比较它们在评价指标上的效果。 文中引入了偏差率和平均偏差率分析它们之间的显著效果。偏差率是表示各种方法计算的相似度和标准相似度(文中使用专家标记的相似度)之间的偏差,局部反映了文本之间语义相似度的稳定程度和正确性。而平均偏差率是从整体上去反映文本之间语义相似度的稳定程度和正确性。偏差率和平均偏差率的具体计算过程分别如式6和式7所示: (6) 平均偏差率= (7) 其中,由于计算的相似度范围在[0,1] 之间,所以相似度的总量度恒等于1。 对文中的相似度方法和胡宝顺的相似度计算方法绘制折线图,具体如图3所示。 图3 方法对比(1) 对文中的相似度方法和田久乐的相似度计算方法绘制折线图,具体如图4所示。 图4 方法对比(2) 通过分析图3和图4可得:在图3中,基于依存关系与同义词词林相结合的语义相似度计算方法相比胡宝顺的相似度方法在偏差率上有了小幅度的降低;在图4中,文中方法相比田久乐的相似度方法在偏差率上有了大幅度的降低,同时文中方法相比田久乐的相似度方法在折线图上的上下幅度波动明显较小,说明文中方法的稳定性相有了明显的提高。通过分析可得,文中的相似度方法和胡宝顺的相似度方法都使用了依存关系计算文本的相似度,在计算相似度的过程中增加了语序结构,计算所得的文本相似度更能反映出语义层面的含义,所以两种相似度方法在偏差率和稳定性上的差别不是很大。但是文中方法在胡宝顺的方法的基础上增加了基于同义词词林的词语语义相似度,在计算文本的相似度过程中不仅考虑了语义结构,而且还考虑了词形之间的词义信息,所以相比较胡宝顺的方法在相似度的偏差率上有了小幅度的降低。但是田久乐的相似度计算方法是基于同义词词林计算文本的相似度,只考虑了词形的词义信息,忽略了语义结构对文本相似度的影响,所以田久乐的相似度计算方法不仅在偏差率上还是在稳定性上都不如文中的相似度计算方法。 使用式7分别计算文中相似度方法、胡宝顺的相似度方法和田久乐的相似度方法的平均偏差率,文中相似度方法的平均偏差率为13.83%,略低于胡宝顺相似度方法的平均偏差率14.36%,明显低于田久乐相似度方法的平均偏差率32.92%。因此,提出的结合依存关系与同义词词林的语义相似度计算方法,不但可以缩小与标准相似度之间的偏差率,同时可以提高该方法的稳定性。 笔者针对语义相似度计算方法的研究,设计了一种基于依存关系与同义词词林相结合的语义相似度计算方法,并在某高中历史科目中进行实验验证。通过实验分析可得,该方法的准确率相比较基于同义词词林的语义相似度和基于依存关系的语义相似度有了一定的提高。但是,笔者发现该方法虽然对于所有学科都能使用,但是由于各学科中的差异性,所以造成计算的精确性不是很高。在今后的研究中,可以根据不同的学科选择不同的相似度方法进行相似度计算,这样可以大大地提高相似度的精度。

3 实验结果与分析
3.1 实验数据
3.2 实验结果与分析



4 结束语
