结合密钥和随机标准正交基的音频伪装方案

邵京津，邵利平，任平安

(陕西师范大学 计算机科学学院，陕西 西安 710119)

1 概 述

针对图像音频信息安全，人们已提出多种安全保护方法，如加密[1-3]、分存[4]、密写[5]和伪装等。相对于其他图像音频保护方法，伪装是将机密图像音频伪装成有意义的非机密图像音频，从而在传输时不易引起攻击者的注意，减少潜在攻击的可能性。

Tangram方法，也称七巧法或中国拼图方法[6-7]，是一种典型的基于变换的图像伪装方法。但传统Tangram方法在匹配过程中需全局搜索，计算复杂度高，等距变换数量少，制约了将密图转变为公开图像的匹配精度。

为降低Tangram方法的搜索时间和加快编码速度，文献[8]添加了块均化操作，在减小计算代价的同时也减少了等距变换数量，导致匹配精度降低。为进一步降低搜索代价，提高编码速度，文献[9]将三角剖分用于对图像三角区域近似重建，尽管免除了全局搜索，但也降低了密图重构精度。文献[10-12]利用2维双尺度矩形映射确定密图子块和公开图像子块间的对应关系，通过直接最小2乘法匹配避免了全局匹配，编码代价远低于传统Tangram方法，但依然仅提供有限的等距变换，导伪装图像视觉质量不高。

Tangram方法也被进一步拓展为音频伪装方法。文献[13-14]分别通过图像子块和音频小段序列构造旋转向量来增加正交等距变换的数量，在提高匹配精度和公开载体伪装质量的同时保证了秘密信息的重构精度，但等距变换所能提供的元素组合十分有限且非全部组合，因此无法找到所有向量元素组合的最优解，同时由于向量旋转所产生的多个等距变换向量都需进行最小2乘匹配，从而提高了计算代价。为减少等距变换数量，文献[15]引入排序线拟合使得排序后公开音频元素和秘密音频划分的小段序列变化趋势保持一致，在避免高昂匹配代价的同时，也提高了拟合匹配精度。

但无论是标准Tangram算法[6-7]，还是Tangram的改进算法[8,10-15]，这些方法所基于的变换模型都是仿射变换模型。对于图像，仿射变换模型只有均值块和差异块，对于音频，只有均值向量和差异向量，且无论是均值块和差异块还是均值向量和差异向量都不满足基本的正交关系，导致变换精度低，不能有效地保证拟合精度，从而无法有效地进行信道欺骗和保证秘密图像音频的重构精度。除此以外，对于恒值块或恒值序列，文献[13-15]需添加扰动来改善匹配性能，由此进一步限制了仿射变换模型的变换精度。对于文献[9]，只能对密图三角剖分区域进行近似重构，其实际应用价值较小。

针对以上问题，文中首先将秘密音频和公开音频划分为同等数量的小段序列，利用密钥来构造随机标准正交基；其次通过求取秘密音频小段序列在随机标准正交基上的投影来对秘密音频小段序列进行充分有效的线性表达，从中选取幅值和能量较大且包含均值的前k个投影系数来表达秘密信息并记录对应的索引位置；再次将选定的投影系数和索引位置序列通过EMD-q嵌入方法嵌入到与之对应的公开音频小段序列中，从而形成信道公开传输音频；最后通过公开传输音频提取的变换参数并结合密钥来对秘密音频重构。同现有方法相比，所提方法可实现秘密音频不同精度的重构并严格依赖于用户密钥，只有掌握正确密钥的用户才能进行高精度的重构。

2 所提方法

文献[6-15]基于的仿射变换模型仅包含均值向量和差异向量，且不满足基本的正交关系，导致拟合精度较低；文献[9]仅能对密图三角剖分区域进行近似重构，导致其实际应用价值较小；文献[13-15]添加扰动来改善恒值块或恒值序列的匹配性能，导致变换精度降低。针对上述问题，文中将秘密音频小段与密钥产生的随机标准正交基进行拟合投影，记录幅值较大系数及其对应的位置索引为变换参数，再通过EMD-q密写方法将变换参数嵌入到公开音频小段中，不仅解决了均值向量和差异向量不满足基本的正交关系所带来的拟合精度较低的问题，还避免了恒值块和恒值序列加噪处理，且所提方法可根据实际需要选取多个正交基对秘密音频进行表达，从而可实现秘密音频不同精度的重构且所提方法严格依赖于密钥，只有特定用户才能对秘密音频进行高精度重构。

2.1 嵌密阶段

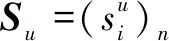
将gu作为密钥，生成n×n维随机矩阵X'，将X'的第0行所有元素置为1，按式1对X'进行行标准施密特正交化，即将X'的每一行转换为标准正交向量：

X=Schimidt(X')

(1)

其中，函数Schimidt()为行标准施密特正交化函数。

(2)

(3)

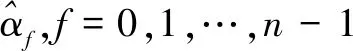
记lr为ri对应的q进制数序列长度，由式4确定：

lr=「logqn⎤

(4)

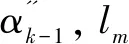
(5)

其中，“[]”为四舍五入取整函数。

lm=「logq2r⎤

(6)

(7)

(8)

(9)

(10)

lpow≤

⎣(N-(lr+lsign+lint)×(k-1)-lm)/(k-1)」

(11)

EMD-q(ri,Pu[lm+ilr,lm+(i+1)lr-1])

lsign)+lm+(i+1)lpow-1]=

(k-1)(lr+lsign)+lm+(i+1)lpow-1])

Pu[lm+(k-1)(lr+lsign+lpow)+ilint,lm+(k-1)(lr+lsign+lpow)+(i+1)lint-1]=

(12)

其中，函数EMD-q()即为EMD-q全方位扩展嵌入函数，其执行的功能是在长度为d的10进制数所构成的元素序列中，通过对每个元素进行±q/2范围内的调整嵌入d位q进制数，其具体定义见文献[15]。

2.2 恢复阶段

(13)

其中，EMD-q-1()为EMD-q()对应的恢复函数，用于从长度为d的10进制数所构成的元素序列中提取出d位q进制数，其具体定义见文献[15]。

(14)

(15)

当得到了α0,α1,…,αk-1和R=(ri)k-1，就可进一步利用密钥Key生成随机序列G=(gu)l生成的标准正交矩阵X来重构秘密音频，其具体方法是：

首先由密钥Key生成随机序列G=(gu)l，将gu作为密钥，生成n×n的随机矩阵X'，将X'的第0行置为1，对X'按式1进行行标准正交化后得到X。

其次利用序列R=(ri)k-1从矩阵X中选取对应的行Xri，得到k-1个1维序列，记为Yi,i=0,1,…,k-2，并将矩阵X中X0记为Yk-1。

最后按式16将Yi,αi,i=0,1,…,k-1转换为秘密音频对应的小段序列Su：

(16)

3 完整的结合密钥和随机标准正交基的音频伪装与恢复算法

结合第2节的工作，以下给出完整的结合密钥和随机标准正交基的音频伪装与恢复算法，记为算法1和算法2。

算法1：结合密钥和随机标准正交基的音频伪装算法。

(1)将长度为l·n的秘密音频S和长度为l·N的公开音频P分别划分为长度为n和N的小段序列Su和Pu，由密钥Key生成随机序列G=(gu)l，初始化u=0；

(2)将gu作为密钥，生成n×n的随机矩阵X'，将X'的第0行所有元素置为1，然后按式1对X'进行行标准施密特正交化后得到X；

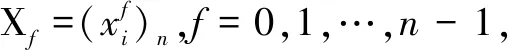
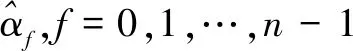
(5)将ri通过lr位q进制数进行表达；

(6)按式7将αi,i=0,1,…,k-1进行q进制数表示；

算法2：结合密钥和随机标准正交基的音频恢复算法。

(2)将gu作为密钥，依次生成n×n的随机矩阵X'，将X'的第0行置为1，对X'按式1进行行标准正交化后记为X；

(3)从Pu中按式13和式15提取出隐藏变换参数R=(ri)k-1和q进制数表示的αi,i=0,1,…,k-1，并进一步将其转换为10进制数αi,i=0,1,…,k-1，然后利用这些恢复出的变换参数按式16重构秘密音频小段序列Su，置u=u+1；

(4)重复第2到3步，直至u=l，然后将所有的小块Su,u=0,1,…,l-1依次拼接作为解密后的秘密音频S输出。

同文献[6-8,10-15]采用的仿射变换模型相比，所提方法的变换精度更高，且随着选取的幅值系数增多，恢复的秘密音频的听觉质量也越来越好；所提方法也避免了文献[13-15]添加扰动导致的变换精度降低，且所提方法严格依赖于密钥，只有特定用户才能对秘密音频进行高精度的重构。

4 实验与结果分析

以下对所提策略进行实验验证，操作系统为Windows 10，CPU为Intel(R) Core(TM) i5-6600 4核CPU，内存为8.00 GB，编码语言为JAVA jdk1.8.0_65。

测试音频由百度随机搜索的WAV音频通过Audacity软件转码得到，为采样频率为44 100 Hz，单声道16位波形音频：告白气球和倾尽天下，并依次编号为A、B。采用信噪比(SNR)和方差(σ)来衡量音频差异和听觉质量。其中SNR按式17计算，σ按式18计算。

(17)

(18)

为验证所提方法的有效性，首先将秘密音频和公开音频(见图1)截取对应长度的采样数据按算法1进行嵌入，并按算法2恢复秘密音频。

图1 实验测试音频

图2给出了实验测试音频波形图，与之对应的实验参数和测试结果衡量如表1所示。

表1 不同划分小段序列长度实验测试参数和实验测试结果

图2 不同划分小段序列长度实验测试音频

从表1和图2可看出，通过文中方法可将音频A嵌入到音频B中，且嵌入参数的伪装频音与原始公开音频波形图只有细微差别，并且从伪装音频中提取参数恢复出的秘密音频与原秘密音频的波形图也极为相似。

从表1可看出，伪装音频的质量相对于原公开音频的值信噪比大于63 dB，方差在1.3左右，说明伪装音频质量极好，且只嵌入了恢复秘密音频的参数，减少了数据嵌入量。而恢复音频相对于原秘密音频，编号1和2的信噪比为20 dB左右，方差在1 000左右，编号3和4的信噪比在27 dB左右，方差在400左右，恢复音频依然具有较好的听觉质量，几乎听不到杂音。原因是文中对秘密音频小段进行拟合的是随机标准正交基，保证向量严格正交，避免了投影存在交叠，从而拟合精度更高，因此提高了秘密音频的重构精度。

图3给出了不同k取值对应的不同精度重构的测试音频波形图，与之对应的实验参数和测试结果如表2所示。

表2 重构精度实验测试参数和实验测试结果

图3 重构精度实验测试音频

从图3和表2可以看出，通过算法1和算法2可正确进行音频伪装和恢复，对于k的不同取值，音频可进行不同精度的重构，且k值越大，恢复的秘密音频精度也越来越高。从表2中编号1、2可看出，对于同等长度划分的小段序列，用以重构的标准正交基越多，即k取值越大，重构精度越高，方差越小，编号4中重构精度有32 dB，远高于文献[15]20 dB左右。对于信道中传输的嵌密公开音频，当k值越大时，嵌密音频的听觉质量下降。原因是文中选取了更多的基用于重构，从而造成了更多参数的嵌入，由此嵌密音频的信噪比随k值增大而降低，但其仍保持在65 dB左右，方差也保持在1.3左右，仍具有良好的听觉质量。因此，文中在提高秘密音频重构精度的同时，还有效平衡了嵌密公开音频的听觉质量。

图4 不同密钥重构精度实验测试音频

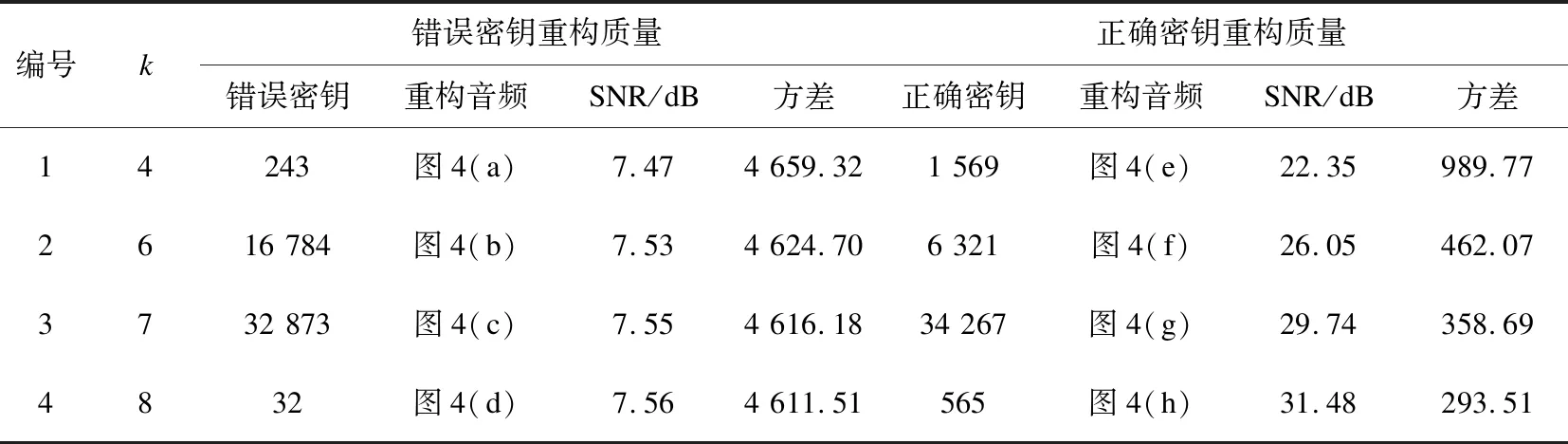
表3 不同密钥测试参数和实验测试结果

图4给出了对于不同密钥对重构精度影响的实验测试音频波形图，与之对应的实验参数和测试结果如表3所示。

从图4和表3可以看出，只有掌握正确密钥才能对秘密音频实现高精度的重构。对于错误密钥，重构的密音频信噪比仅在7.5 dB左右，方差高达4 600，说明恢复音频听觉质量极低，具有大量杂音，且当密钥错误时，不管k取值多少，都无法正确高精度地恢复秘密音频。而对于正确的密钥，信噪比为27 dB左右，说明恢复的秘密音频听觉质量较高，几乎听不到杂音。且在密钥正确的前提下，可根据需求选取不同k值，实现不同精度的秘密音频重构。

5 结束语

传统基于Tangram的音频伪装方法变换精度低且不满足基本的正交关系，从而无法保证秘密音频与公开音频之间的拟合精度，同时当分段变换音频为恒值序列时，需添加扰动以保证变换后音频的恢复质量，由此会降低信道传输音频质量。为避免上述问题，提出一种结合密钥和随机标准正交基的音频伪装方法。首先对秘密音频和公开音频分段，利用密钥构造随机标准正交基；其次通过秘密音频小段在随机标准正交基上的投影来对秘密音频小段进行表达，从中选取包括均值幅值较大的前k个投影系数，并记录对应的索引位置；再次通过EMD-q密写方法嵌入到对应的公开音频小段中形成信道公开传输音频并通过信道公开传输音频提取变换参数和通过密钥重构秘密音频。实验表明，所提方法可充分利用随机标准正交基重构不同精度的秘密音频，且随着选取的幅值系数增多，恢复的秘密音频质量也越来越高，同时所述策略严格依赖于密钥，只有掌握正确密钥的用户才能进行高精度的重构。