The Effects of Wettability on Primary Vortex and Secondary Flow in Three-Dimensional Rotating Fluid∗

Si-Hao Zhou (周思浩),Wen Qiu (邱文),Yong Ye (叶勇),Bing He (何冰), and Bing-Hai Wen (闻炳海)

Guangxi Key Lab of Multi-Source Information Mining ＆ Security,Guangxi Normal University,Guilin 541004,China

Department of Computer Science and Information Engineering,Guangxi Normal University,Guilin 541004,China

Abstract The secondary flow driven by the primary vortex in a cylinder,generating the so called“tea leaf paradox”,is fundamental for understanding many natural phenomena,industrial applications and scientific researches.In this work,the effect of wettability on the primary vortex and secondary flow is investigated by the three-dimensional multiphase lattice Boltzmann method based on a chemical potential.We find that the surface wettability strongly affects the shape of the primary vortex.With the increase of the contact angle of the cylinder,the sectional plane of the primary vortex gradually changes from a steep valley into a saddle with two raised parts.Because the surface friction is reduced correspondingly,the core of the secondary vortex moves to the centerline of the cylinder and the vortex intensity also increases.The stirring force has stronger effects to enhance the secondary flow and push the vortex up than the surface wettability.Interestingly,a small secondary vortex is discovered near the three-phase contact line when the surface has a moderate wettability,owing to the interaction between the secondary flow and the curved gas/liquid interface.

Key words: secondary flow,lattice Boltzmann method,multiphase flow,rotating fluid

1 Introduction

Stirring a cup of tea,the liquid is made to rotate and the leaves will soon collect in the center of the bottom,instead of the brim.The common and interesting phenomenon is called as “tea leaf paradox” and was used by Albert Einstein to explain the formation of meanders in the courses of rivers,in which the secondary flows play a key role.[1]The stirring makes a fluid system mixing or separation evolving from one state to another.The resulting secondary flow,which follows the primary flow or vortex,is fundamental for understanding atmospheric pressure systems and river course erosions,separating red blood cells from plasma or coagulated trub from beer in the brewing technique.[2]Jakubowskiet al.studied the secondary flow in a whirlpool cycling vat,which is employed to remove hot trub in the process of wort boiling.[3]Tayloret al.used the dynamic filter made by the secondary flow principle in the coaxial double cylinder to implement the liquid extraction function.[4]Najjariet al.investigated a steady flow through a curved pipe using perturbation theory and found that there are two counter-rotating vortices in the cross section of the pipe.[5]Kefayatiet al.studied the effects of secondary flow and eddy current on cerebral venous blood bank by utilizing imaging techniques.[6]Westraet al.analyzed the secondary flow in a centrifugal pump impeller by performing the CFD simulations.[7]On the other hand,the secondary flow has become an important technology in inertial microfluidics.[8]Di Carloet al.realized crossstream inertial migration in a micrometer winding tube,in which the secondary flow is used to accelerate the particle focusing.[9]Xianget al.applied spiral microfluidic channels,in which the steady secondary flow promotes the particle focusing all the time.[10]Liuet al.analyzed the role of the secondary flow in tubes with different shapes.[11]Chunget al.created a sheathless and high-throughput microparticle focusing platform through geometry-induced secondary flows.[12]Sunet al.studied the inertial secondary flow in curved channel by the lattice Boltzmann method(LBM).[13]As the central equation in kinetic theory,the Boltzmann equation offers the possibility to simulate complex flows with a wide range of spatiotemporal scales in an effective and accurate way.[14]Over the past three decades,the LBM has been developed and modified with great enhancements in terms of precision and/or efficiency.[15]

2 Model and Method

In this work,the flow in a rotating fluid with free interface is investigated.We focus on the effects of the surface wettability on the primary flow and the secondary vortex and hope to extend its applications in micro scale.The fluid system is modeled by the multiphase LBM driven by a chemical potential.The single-relaxation-time lattice Boltzmann equation can be concisely expressed as[16]

whereτis the relaxation time,Fis the external force term,andis the equilibrium distribution function,fi(x,t) is the particle distribution function at lattice sitexand timet,eiis the discrete speeds withi=0,...,N.

whereωiis the weighting coefficient anduis the fluid velocity.The nonideal force in a van der Waals fluid can be evaluated from the free energy,which determines the general expression of equation of state (EOS)[17]

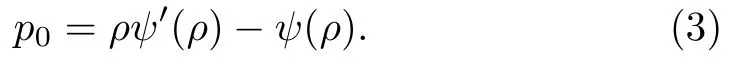
The full pressure tensor can be written as

whereδαβis the Kronecker delta.The chemical potential can also be defined from the free energy as[18−20]

where

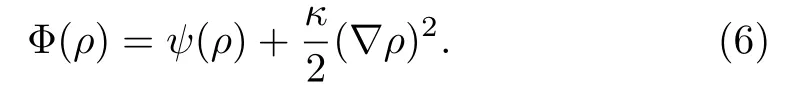
Then,the chemical potential can be calculated by the freeenergy density

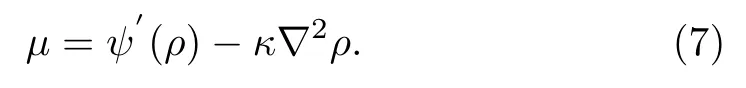
Thus,the nonideal force can be easily evaluated by the chemical potential avoiding the pressure tensor[21]

Correspondingly,the macroscopic fluid velocity is redefined by the averaged momentum before and after the collision

It is verified that the multiphase model satisfies thermodynamics and Galilean invariance.[21]The water/vapor system is constrained by the famous Peng-Robinson (PR)EOS,

where the temperature function isα(T)=[1+(0.37464+1.54226ω −0.26992ω2)·with the acentric factorω= 0.344 for water.The parameters takea= 2/49,b= 2/21 andR= 1.Correspondingly,the chemical potential is written as[21]

Figure 1 illustrates a schematic diagram of threedimensional rotating fluid in a cylinder.We selected the three-dimensional LBM with 19 discrete velocities.A relaxation time is 1.3 and the temperature isTr=0.8.Both the length and width of the computational domain are 60 lattice units and the height is 120 lattice units.The cylinder radius is set asR=30 lattice units,R∗denotes radial position.The fluid is driven to rotate by a stirring force,which is exerted atr=20 lattice units away from the central axis of the cylinder.The chemical-potential boundary condition is used on the surface of the cylinder,and the chemical potential of the cylinder surface is specified to determine the wettability of the cylinder.[20]

Fig.1 (Color online) Three-dimensional rotating fluid in a cylinder.

In the simulation experiment,we set the upper part of the cylinder to the gas phase and the lower part to the liquid phase with higher density.By changing the chemical potential of the wall and the bottom in our model,we can obtain the different contact angle and observe the effects of the wettability on the primary flow and the secondary vortex.The stirring force in the cylinder is set asF=0.0018 and the contact angle of the wall and the bottom is set as 30◦,60◦,90◦,and 150◦,respectively.From Fig.2,we can observe the formation of the secondary flow in the vertical cross section.When the contact angle is 30◦that the wall is hydrophilic,the liquid is easily attracted by the surface and spreads on the wall,the shape of the primary vortex appears as a steep valley as shown in Fig.2(a).As the contact angle increases,the wettability of the wall surface becomes hydrophobic,the liquid leaves the wall of the cylinder and the shape of primary vortex gradually becomes a saddle with two raised parts.Meantime,as the increase of contact angle,the concave liquid level rises gradually.Figure 3 draws a series of shapes of the primary vortexes when the surface wettability of the channel side is changing from hydrophilic into superhydrophobic.Interestingly,a small secondary vortex is discovered near the three-phase contact when the surface has a moderate wettability;it gradually weakens and disappears when the surface becomes strong hydrophilic or hydrophobic.This indicates that the formation of the small vortex is affected by the contact angle of wall and is result of the interaction between the secondary flow and curved gas/liquid interface.

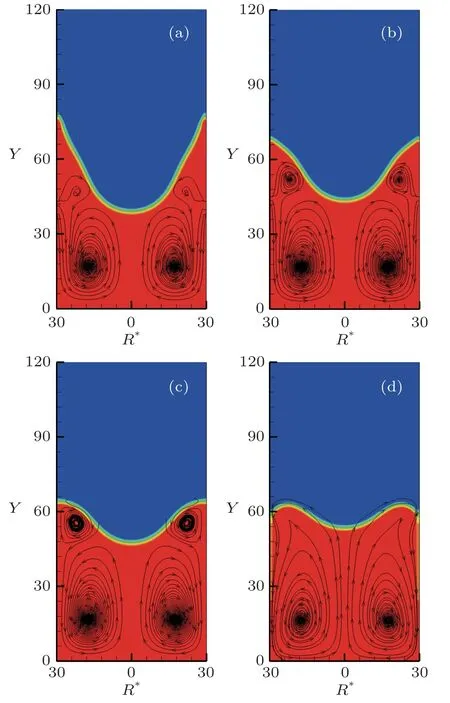
Fig.2 (Color online) The primary vortex and the secondary flow at different contact angles,(a)θ = 30◦,(b)θ =60◦,(c)θ =90◦,(d)θ =150◦.

The big secondary vortex can always exist; its position and vorticity are influenced by the surface wettability of the cylinder.In order to investigate the influence of surface wettability on the vortex position and vorticity,the flows in the cylinders with three different volumes are simulated and analyzed.Namely,the heights of the liquid level in three different volumes are 50,60,and 80 lattice unites,respectively.The effects of different surface wettability of side wall and bottom are investigated separately.Firstly,the surface wettability of the cylinder bottom remains neutral,namely the contact angel 90◦,whereas the contact angle of the side wall changes from 30◦to 160◦with the increment 10◦every time.Figure 4 shows the influence of the surface wettability of side wall on the vortex position and intensity.The trends of the three different liquid heights are consistent,especially the vorticities of them are almost the same.The more hydrophobic the cylinder side is,the stronger the vortex intensity is,and the nearer to the centerline and bottom the vortex core is.When the contact angle increases,the wetting property of the side surface changes from hydrophilic into hydrophobic.These bring down the friction of the side surface,[23]and then enhance the secondary flow.Similarly,the side friction decreases,the rotation speed increases,the secondary flow vortex moves down and the bottom friction increases.

Fig.3 (Color online) The shapes of the primary vortexes are changing with the different wettability of the side surface.

Secondly,the surface wettability of the cylinder side remains 90◦,while the contact angle of the bottom changes from 30◦to 160◦with the increment 10◦every time.As shown in Fig.5,although the more hydrophobic bottom makes the secondary vortex stronger and pulls the vortex core nearer to the centerline and bottom,the heights of the vortex core for different liquid volumes are clearly different.Furthermore,both the decrease of the vortex core and the increase of the vortex intensity caused by the growth of the bottom contact angle are slow than those by the side surface.On the whole,the wetting effect of the cylinder side is more intensive than the bottom.

At last,the influence of the stirring force on the secondary flow is studied.The contact angles of the side and bottom surface remain 90◦,while the stirring force changes from 0.0014 to 0.0024.As shown in Fig.6,the influences of stirring force on the secondary flow are highly consistent for three different liquid level heights.Although the horizontal position of the secondary vortex only moves a little,its height is raised evidently and the vortex intensity has a substantial increased too.With the increase of the stirring force,the angular velocity is larger and larger,and then the bigger centrifugal force pushes the liquid to the cylinder side.The center of the primary vortex drops and the edge rises notably.Consequently,the vortex core of the secondary flow is pushed up and enhanced greatly.

3 Conclusion

Fig.4 (Color online) The impacts of the wettability of side wall on (a) vortex core and (b) the intensity of the vortex.The curve in black,red,and blue represent liquid level at 50,60,80 lattice unites,respectively.

Fig.5 (Color online) (a) The impacts of the bottom wettability on the vortex position of the cylinder and (b) on the strength of the vortex.

Fig.6 (Color online) (a) The influence of stirring force on the position of the vortex core and (b) on the strength of the vortex.

In this work,the multiphase LBM driven by a chemical potential is used to study the flow of rotating fluid in a three-dimensional cylinder.Through a series of numerical simulations,the effects of stirring force and surface wettability on primary vortex and secondary flow are presented clearly.It can be concluded that when the stirring force is constant,the contact angle has a positive correlation with the position of secondary flow and the vortex intensity,and the surface wettability affects the shape of the primary vortex.The increase of the stirring force also enhances the secondary flow and pushes the vortex up.Remarkably,we find there is a small secondary vortex near the three-phase contact line when the surface has a moderate wettability,owing to the interaction between the secondary flow and the curved gas/liquid interface.The research on secondary flow not only helps us to explain the natural phenomena,but also has important significance for the related performance improvement in industrial production and medical research,especially in inertial microfluidics.