Uncertainty Relations for Coherence∗

Shun-Long Luo (骆顺龙) and Yuan Sun (孙源)

Academy of Mathematics and Systems Science,Chinese Academy of Sciences,Beijing 100190,China

School of Mathematical Sciences,University of the Chinese Academy of Sciences,Beijing 100049,China

Abstract Quantum mechanical uncertainty relations are fundamental consequences of the incompatible nature of noncommuting observables.In terms of the coherence measure based on the Wigner-Yanase skew information,we establish several uncertainty relations for coherence with respect to von Neumann measurements,mutually unbiased bases (MUBs),and general symmetric informationally complete positive operator valued measurements (SIC-POVMs),respectively.Since coherence is intimately connected with quantum uncertainties,the obtained uncertainty relations are of intrinsically quantum nature,in contrast to the conventional uncertainty relations expressed in terms of variance,which are of hybrid nature (mixing both classical and quantum uncertainties).From a dual viewpoint,we also derive some uncertainty relations for coherence of quantum states with respect to a fixed measurement.In particular,it is shown that if the density operators representing the quantum states do not commute,then there is no measurement(reference basis) such that the coherence of these states can be simultaneously small.

Key words: uncertainty relations,coherence,Wigner-Yanase skew information,quantum uncertainty,von Neumann measurements

1 Introduction

The Heisenberg uncertainty principle arising from incompatible (noncommuting) observables asserts a fundamental limit to quantum measurements,and is one of the characteristic consequences of quantum mechanics with deep connections to the Bohr complementarity principle.Uncertainty relations,as manifestations of the Heisenberg uncertainty principle,have been extensively and intensively studied with a wide range of applications in many fields.For example,it is closely related to quantum measurement and signal processing,[1−2]preparation of state,[3]complementarity,[4−5]entanglement detections,[6−9]quantum coherence,[10−13]quantum non-locality.[14−16]There are various quantitative characterizations of uncertainty relations such as entropic uncertainty relations,[17−20]uncertainty relations based on variance and the Wigner-Yanase skew information,[21−25]and so on.

Coherence is intrinsically related to superposition which differentiates quantum mechanics from classical mechanics.In recent years,there are increasing interests in quantitative studies of coherence.[26−40]As a kind of quantum resource,coherence plays an important role in a variety of operational applications in asymmetry,[41−45]metrology,[46]quantum key distributions,[47]thermodynamics,[48−50]quantum computation and communication.[51−53]

Since coherence of a quantum state depends on the choice of measurements (reference bases),it is natural to study the relations of coherence between two or more different measurements,or coherence of different states with respect to a fixed measurement.In fact,there are several investigations on uncertainty relations for quantum coherence,[10−13]as well as the complementarity of coherence in different bases.[54−55]Based on the skew information introduced by Wigner and Yanase,[56]an informationtheoretic measure of coherence has been introduced in Refs.[35–37] (see Sec.2),which has an operational interpretation as quantum uncertainty,in sharp contrast to the conventional notion of variance(which usually involves both classical and quantum uncertainties).The aim of this paper is to employ this coherence measure to characterize uncertainty relations for coherence in an intrinsically quantum fashion.

The paper is organized as follows.In Sec.2,we establish several uncertainty relations for coherence with respect to arbitrary von Neumann measurements(orthonormal bases),as well as with respect to mutually unbiased bases (MUBs).In Sec.3,we study coherence with respect to general symmetric informationally complete positive operator valued measurements (SIC-POVMs),and derive the corresponding uncertainty relations.We obtain some uncertainty relations for several quantum states with respect to a common measurement in Sec.4.Finally,we summarize in Sec.5.

2 Uncertainty Relations for Coherence with Respect to von Neumann Measurements

Letρbe a quantum state (density operator) and Π=be a von Neumann measurementconstitutes an orthonormal basis for the system Hilbert space),then one can consider coherence ofρwith respect to Π.In this paper,we employ the coherence measure

introduced in Refs.[35–37]to characterize uncertainty relations.Here

is the skew information introduced by Wigner and Yanase in 1963,[56]His an arbitrary observable (Hermitian operator).It is remarkable that the skew information enjoys many nice properties and has several interpretations as non-commutativity (betweenρandH),quantum Fisher information (ofρwith respect toH),asymmetry (ofρwith respect toH),quantum uncertainty (ofHinρ),[21−24,37−38]etc.More generally,for any POVMwe may define a bona fide measure for coherence ofρwith respect toMas[37]

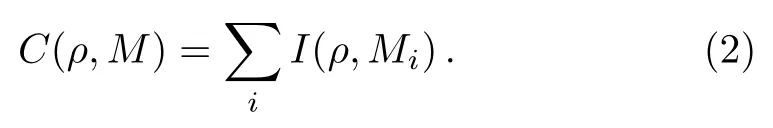
The above measure reduces to that defined by Eq.(1)whenMis a von Neumann measurement.In general,the measurement operators inMmay not be mutually orthogonal projections (e.g.,coherent states in quantum optics and spin systems),and in this caseC(ρ,M) generalizesC(ρ,Π) considerably.

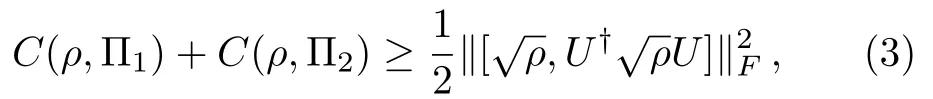
which may be regarded as a kind of uncertainty relations for coherence of the quantum stateρwith respect to the measurements Π1and Π2.Here||A||F= (trA†A)1/2is the Frobenius norm,Uis the unitary operator defined by

To prove inequality (3),we first recall a mathematical result in Ref.[57],Remark 5.1: If one of the matricesAandBis non-negative,then

Similar to the method in Ref.[58],consider the decompositions of the matrices

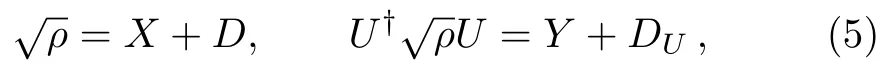
whereDandDUare the diagonal parts ofρandU†ρUrespectively.It is obvious thatX,Yhave zero diagonal elements.Then by inequality (4),the triangle inequality of the norm∥·∥F,and the elementary inequalityx2+y2≥(x+y)2/2 for any real numbersx,y,we have

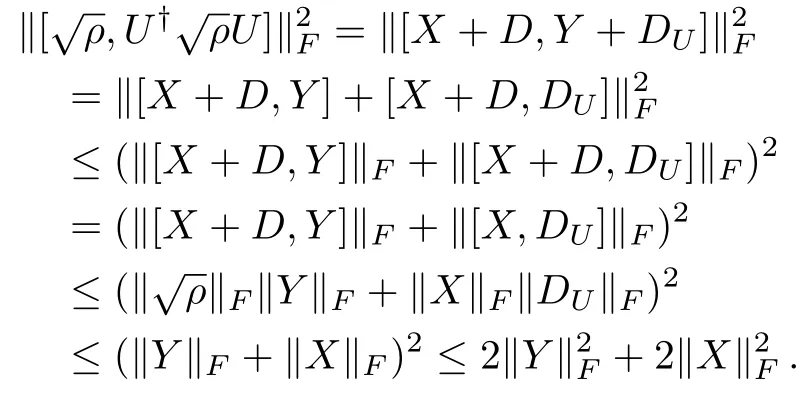
Therefore

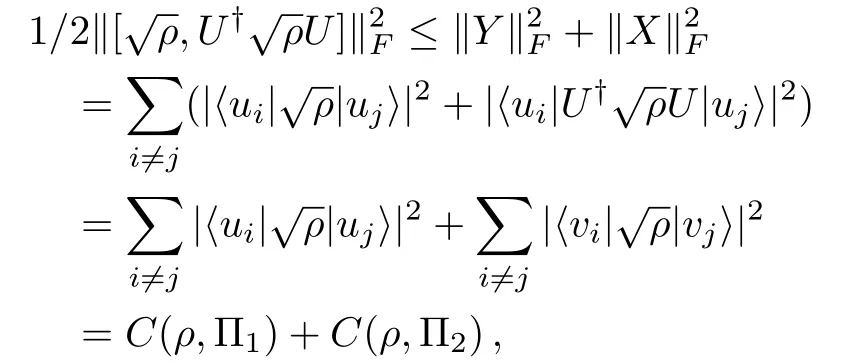
which completes the proof.

From an alternative perspective,we have the following inequality

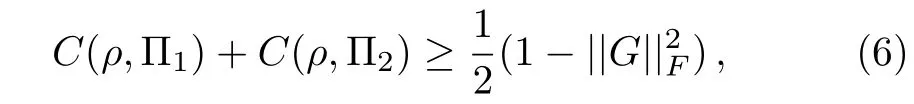
which is also a kind of uncertainty relations for coherence.HereG=D1TD2with

The derivation of inequality (6) is as follows.

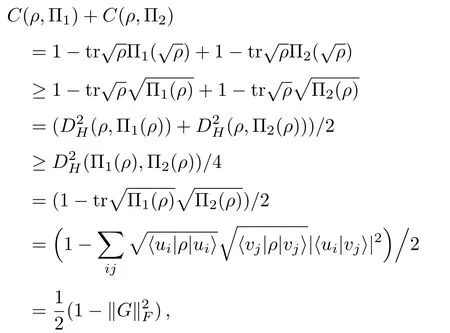
where

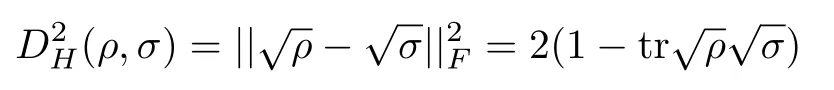
is the square of quantum Hellinger distance betweenρandσ.

The first inequality in the above derivation follows from the Kadison inequality,which states that[59]Φ(A)2≤Φ(A2) for any unital and positive quantum operation Φ and Hermitian operatorA,while the second inequality is obtained by the triangle inequality of quantum Hellinger distance.

Combining the above two uncertainty relations,we have

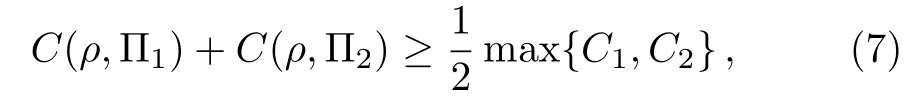
where

Next,we consider coherence with respect to mutually unbiased bases (MUBs).Recall that two orthonormal basesandj= 1,2,...,d}of ad-dimensional system Hilbert space are mutually unbiased if[60−61]

When the dimensiondis a prime power (i.e.,d=pkfor a prime numberpand a positive integerk),there exists a complete set ofd+1 MUBν=1,2,...,d+1.[60−61]

In Ref.[62],we have obtained the following exact uncertainty relation

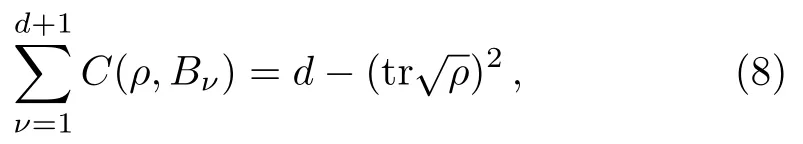
for a complete set of MUBsBν,ν= 1,2,...,d+1.In particular,for any pure stateρ,we have

Here we extend the above exact uncertainty relation to anymMUBsBν,ν=1,2,...,m,as follows

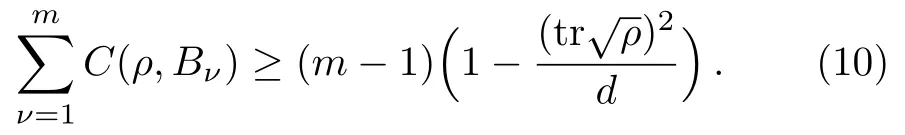
To establish the above result,noting that[63]

Replacingρwithand using the definition ofC(ρ,Bν),we obtain the desired inequality(10).In particular,for any pure stateρ,we have

3 Uncertainty Relations for Coherence with Respect to SIC-POVMs

In this section,we study coherence of a state with respect to a general SIC-POVM,and derive some uncertainty relations for coherence of a state with respect to a family of SIC-POVMs.

Consider ad-dimensional system,letHdbe the set of alld×dHermitian operators andTdbe the set of alld × dtraceless Hermitian operators.A set ofd2nonnegative operatorsP={Pi:i= 1,2,...,d2}(not necessarily of rank 1) is called a general symmetric informationally complete positive operator valued measurement(SIC-POVMs),[64]if

(ii) It is symmetric: trP2i= trP2j1/d3for alli,j= 1,2,...,d2,and tr(PiPj) = tr(PlPm) for alland.

Gour and Kalev have shown that there is a one-toone correspondence between SIC-POVMs and orthonormal bases ofTdin the following sense:[64]Let{Fi:i=1,2,...,d2−1}be an orthonormal base ofTd,that is,trFi= 0 and trFiFj=δij,i,j= 1,2,...,d2−1.Putand

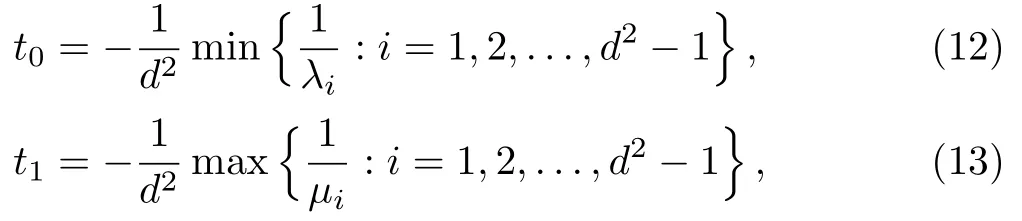
withλiandµithe maximum and minimum eigenvalues ofF −d(d+1)Fi,respectively.For any 0[t0,t1],take

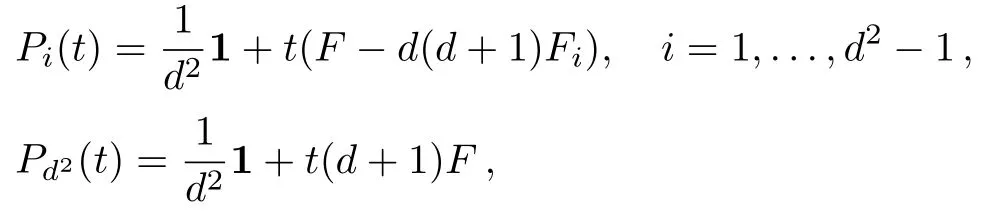
thenP(t)={Pi(t):i=1,2,...,d2}constitutes a general SIC POVM.Conversely,any SIC POVM is of the above form for some orthonormal basis{Fi:i=1,2,...,d2−1}ofTd.TakeF0= 1,then it is obvious that{Fi:i=0,1,2,...,d2−1}is an orthonormal basis for the spaceHdof all Hermitian operators.

With the above preparation,we can state our result for coherence

of the stateρwith respect to the SIC-POVMP(t) ={Pi(t):i=1,2,...,d2}as

wheret ∈[t0,t1].This may be regarded as an exact uncertainty relation for the family of operatorsPi(t) in the stateρ.

To prove Eq.(14),noting that from Ref.[24],we know that

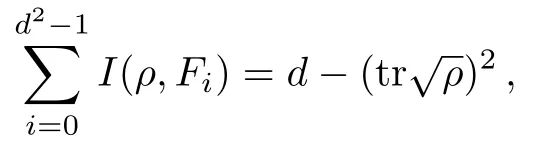
from which we have

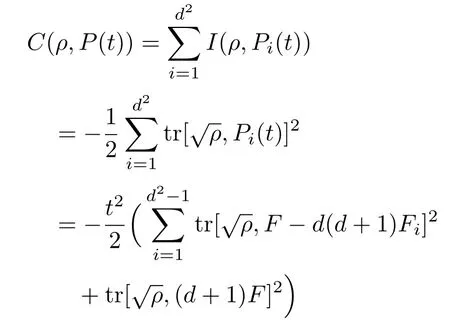
From the above result,we readily obtain that for arbitrarymSIC-POVMsP(ν)(tν),ν=1,2,...,m,wheretνis the correspondingtconstants in their representations in terms of orthonormal bases ofTd,we have

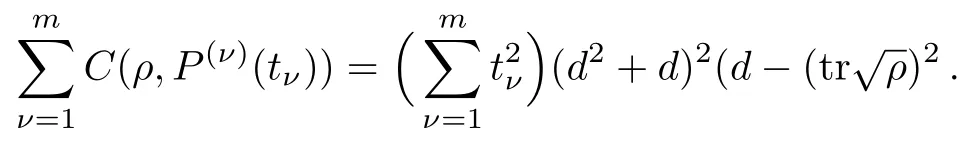
In particular,for any pure stateρ,we have

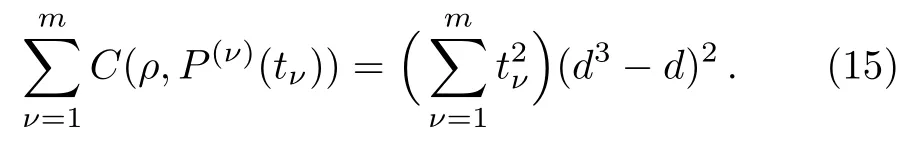
These are uncertainty relations for coherence with respect to several SIC-POVMs.

4 Uncertainty Relations for Coherence of Quantum States with Respect to a Common Measurement

Coherence is a relative concept involving both quantum states and measurements.In the previous sections,we have discussed uncertainty relations with respect to different measurements by fixing a quantum state.From a dual viewpoint,we study uncertainty relations of different quantum states by fixing a measurement in this section,and obtain the following result

which may be regarded as an uncertainty relation for coherence of two quantum states with respect to a common measurement(reference basis).Hereρandσare arbitrary quantum states,and Π ={|i〉〈i|}is any von Neumann measurement.

Equation (16) can be derived by decomposingandas Eq.(5).This shows that,if two states are not commutative,then there is no measurement (reference basis)such that the coherence of these two states can be simultaneously small.

We further reveal a link between uncertainty relations for coherence and quantumness of ensembles.Consider a quantum ensembleE={(pi,ρi):i=1,2,...,n}with

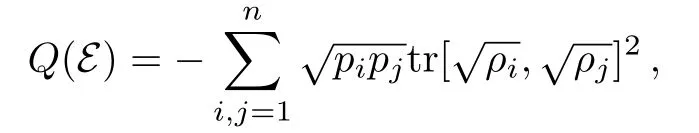
as a measure of quantumness in Ref.[65].Hereρiare density operators andFrom the above discussion,we get that

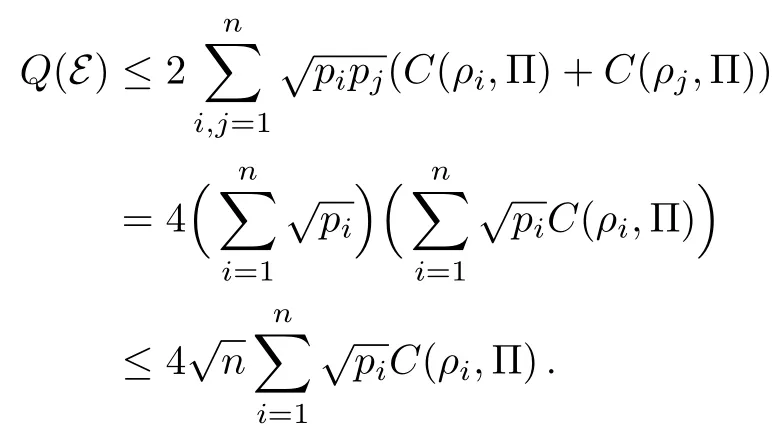
Consequently,the weighted average of coherence

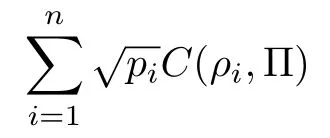
of the quantum ensemble satisfies

This relation sets a lower bound to coherence in terms of quantumness of the quantum ensemble.

5 Summary

By employing the coherence measure based on skew information,we have derived some uncertainty relations with respect to von Neumann measurements as well as with respect to SIC POVMs.In the special cases of a family of von Neumann measurements,we have considered uncertainty relations for coherence with respect to any MUBs (not necessary two MUBs),and have proved that the lower bound is a positive constant for pure states.

From a dual perspective,we have obtained some tradeoff relations for coherence of different quantum states and quantum ensembles with respect to a common measurement.These results imply that if two density operators are not commutative,then there is no reference basis such that their coherence are simultaneously small.

We emphasize that the coherence measure based on the skew information has a natural interpretation as quantum uncertainty,[36−37]consequently the uncertainty relations for coherence obtained here can be regarded as genuinely quantum uncertainty relations.