FEM for Blood-Based SWCNTs Flow Through a Circular Cylinder in a Porous Medium with Electromagnetic Radiation∗
2020-01-09MohamedEidAlHossainyandShZoromba
Mohamed R.Eid, A.F.Al-Hossainy, and M.Sh.Zoromba
1Department of Mathematics,Faculty of Science,Northern Border University,Arar,1321,Saudi Arabia
2Department of Mathematics,Faculty of Science,New Valley University,Al-Kharga,Al-Wadi Al-Gadid,72511,Egypt
3Department of Chemistry,Faculty of Science,New Valley University,Al-Kharga,Al-Wadi Al-Gadid,72511,Egypt
4Department of Chemistry,Faculty of Science,Northern Border University,Arar,1321,Saudi Arabia
5Department of Chemical and Materials Engineering,King Abdulaziz University,Rabigh 21911,Saudi Arabia
6Department of Chemistry,Faculty of Science,Port Said University,42521 Port-Said,Egypt
Abstract This work aims to study magnetohydrodynamic flow through a circular cylinder in a horizontal position of SWCNTs in blood as a base fluid in the existence of non-linear thermal radiation and heat source/sink.Three kinds of nanoparticles shapes are considered.The study is employed the finite element technique to explore and enhance the influences of essential parameters on temperature profiles and is debated the heat transport within blood injects with SWCNTs and exposes to electromagnetic radiation.The treatment with thermal analysis and heat transfer rate being a better substitute more than surgery and chemotherapy for cancer therapy.Utilizing of nanoparticles thermal features is a mounting area of nanomedicine field because of the probable for purposeful demolition of cancer cells.This remedy is relied on many parameters,including nanofluid thermal conductivity,nanoparticles volume fraction,thermal radiation and power and heat source.The numerical solutions for flow and heat transfer features are assessed for diverse governing parameters values.The obtained results are substantiated against the relevant numerical results in the published researches.Results show that both flow velocity and temperature increase for larger values of thermal radiation,heat source and SWCNTs volume fraction with lamina and cylinder shapes.Also,spherical shape of SWCNTs occurs high disturbances in velocity and temperature distribution in the case of cooled cylinder.
Key words: finite element method,heat transfer,blood,SWCNTs,electromagnetic radiation

No menclature

Greek symbols

Subscripts

Abbreviations
1 Introduction
The model of nano-liquid was a new category of liquids with different heat transference features that can be architected by suspended mineral nanoparticles in classic heat transference fluids.The successor fluid acknowledged as nanofluid is potential to demonstrate superscript thermal conductivities versus to those of existing utilized heat transference fluids.The nanoparticles employed in nanofluids are manufactured of metals,like alumina,copper,metal oxides or non-metals (CNTs,graphite) and commonly ethylene glycol,water and blood are employed as basis fluid.CNTs have convened a fundamental role in nanostructures because of their singular mechanical structural and electronical features.CNTs have exceptional conductivity that helps them to constitute a grid of conductive tubes.CNTs have been depreciated as thermal boundary substances for thermal maintain.Highly conductivity CNTs have attracted considerable interest from scientist.CNTs utilized in nanofluids are generally of two kinds,exclusively single-walls CNTs (SWCNTs) and multiple-walls CNTs(MWCNTs).The CNTs width varies from 1 nm to 100 nm and CNTs length is in micrometer.
The research topic of nano-liquids has receipted considerable interest universality.Originally high thermal conductivity is a basic constraint in enhancement energycompetence heat transfer liquids that are desired for ultrahigh-performance heating.A very tiny magnitude of guest nanoparticles,when suspended stably in host liquids,can offer enhancements in the thermal characterizations of the host liquids.Buongiorno[1]suggested a form for nanofluids convective transport integrating the impacts of Brownian motion and thermophoresis diffusion.This form was implemented to the problem of Rayleigh-Benard by Refs.[2–3] and they demonstrated that both Brownian motion and thermophoresis influences perform to transit-diffusion conditions that are in certain methods corresponding to the commonplace Soret and Dufour diffusion that established with a dual liquid.Nanofluids in one and two-phase models in diverse situations with various parameter impacts have been examined by Refs.[4–16].
Heat transference performing of CNT nanofluids flow across a horizontal pipe was achieved by Ref.[17].They existed significant enhancement of heat transference by convection and remarked that the betterment based on Reynolds number and CNTS volume fraction.Meyeret al.[18]provided experimentally the heat transfer improvements of MWCNTs flux via a straight horizontal pipe.The thermal conductivity promotion of engine oil and ethylene glycol with MWCNTs is indicated by Ref.[19].They existed that ethylene glycol-CNTs pendants have the largest thermal conductivities when it compares with ethylene glycol deprived of CNTs.Wanget al.[20]discussed the flow and heat transfer of nanofluids with pressure drop in a horizontal circular tubing including CNTs experimentally.They revealed that nanofluids at lowland concentration reinforce the heat transfer with bit additional sanction in pumping power.The experimental examination of convective heat transfer properties of byproduct refrigerants-depend on CNTs nanofluid in a ducted heat exchanger considered by Ref.[21].
Khanet al.[22]mentioned heat transfer features of CNTs over a flattened plate with boundary conditions of uniformly heat flux and Navier slip numerically,they utilized single and multi-walls CNTs and MWCNTs with three various norm fluids.Al-Haqet al.[23]examined water-based flow with SWCNTs and MWCNTs,they studied a superior heat transfer rate for single and multiple walls CNTs.Kandasamyet al.[24]evidenced numerically the chemical react influence on copper,Al2O3,and SWNTs nanofluid flowing with the conditions of slip by utilizing RKF technique based on shooting approach and the chemical reaction effect on SWCNTs,Al2O3and Cunanoparticles on convective mass transfer in having of water as a base fluid by utilizing numerical regime also deliberated by Ref.[25].Lately,analytical solution of heat transfer improvement in Maxwell nanofluids flow by natural convection with the two types of CNTs past a vertical plate utilizing Laplace transform method provided by Ref.[26].Casson model[27]is determined as the majority favored rheological form for characterizing blood flow of human body.[28−29]Eidet al.[11]elaborated thermal radiation impact on Sisko-model flow of gold nanoparticles in human blood as base fluid.
So far there is no research in the literature on the effect of electromagnetic radiation on SWCNTs-blood nanofluid mixed convection embedded in a porous material with heat source/sink.The presence of electromagnetic radiation on nanofluid usually has the effect of inhibiting the development of destabilization.This paper designed to study the blood flow involving SWCNTs is inspected in the existence of magnetohydrodynamic,thermal radiation,heat source/sink and porosity parameter.The NPs shapes are taken in account in this study.Human blood is adopted as base fluid with SWCNTs insider.
2 Flow Analysis
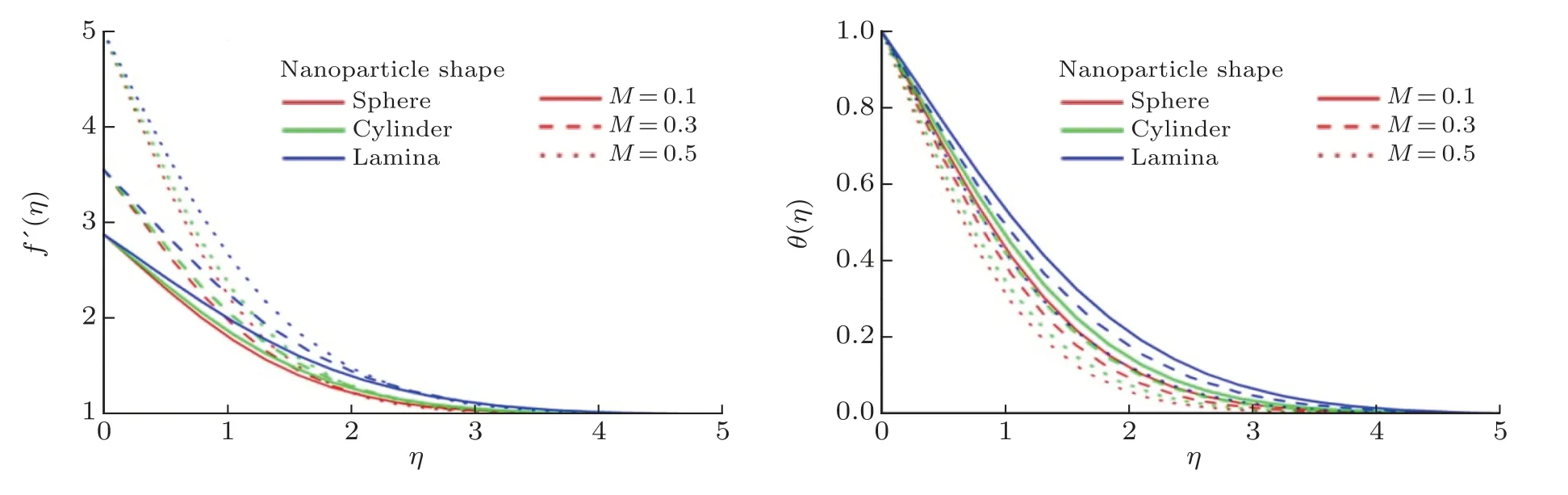
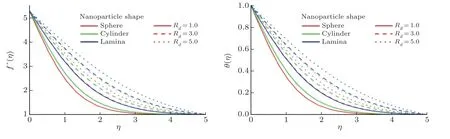
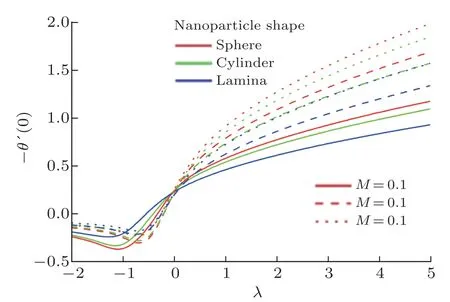
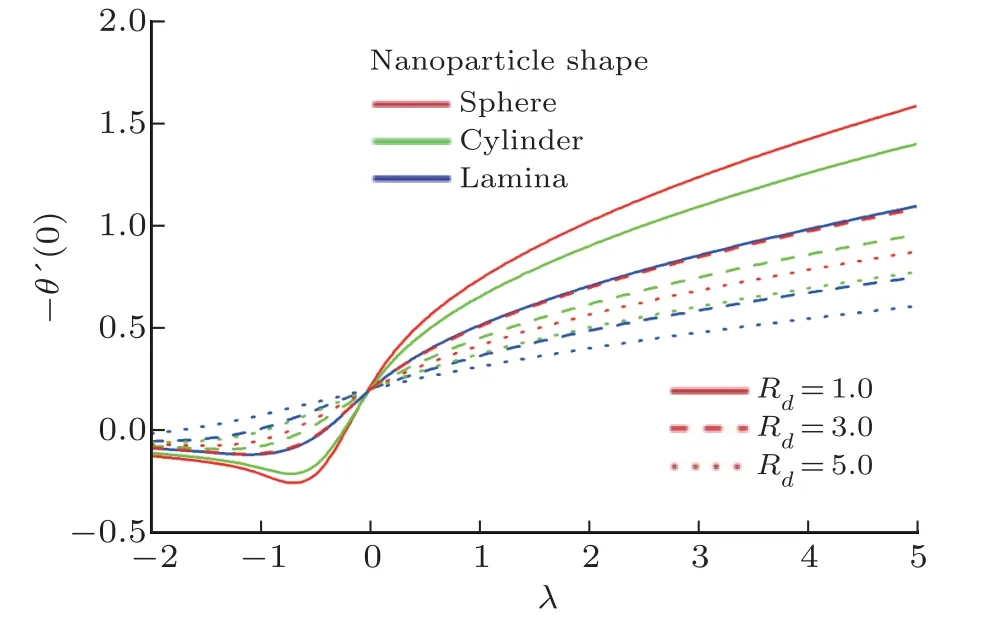
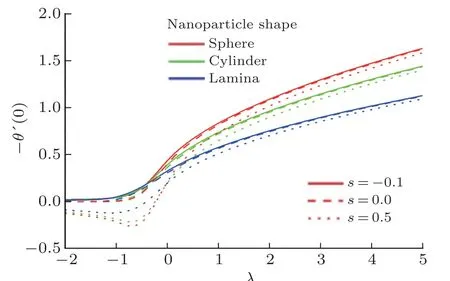
Consider the issue of steady boundary-layer flow of mixed convection over a cooled/heated circular cylinder placed horizontally of radiusrin a porous material saturated with a nanofluid in the existence of applied magnetic field.It is supposed that the external flow velocity is,whereis the coordinate scaled together the cylinder surface starting from the bottom stagnationpoint.Also assumed that the constant temperature of the surface of the cylinder isTw,whereas the value of constant temperature ambient isT∞,whereTw>T∞for the assisting flow(a heated cylinder)andTw Fig.1 (Color online) Flow configuration model. with the associated boundary conditions: whereφis nanoparticles volume fraction,mis nanoparticles shape parameter,µbis the blood dynamic viscosity,ρbandρCNTare the densities of the blood and SWCNTs nanoparticle,σbandσCNTare electric conductivities of blood and SWCNTs,kbandkCNTare thermal conductivities of the blood and SWCNTs,βbandβCNTarethermal expansion coefficients of the blood and nanoparticle,(ρcp)band (ρcp)CNTare the specific heat factors of the blood and SWNTs,respectively. By introducing the following non-dimensional variables: or this equation can be written in the form where M=σbKB20/µbis the magnetic field parameter. λ=Rar/Peis the parameter of mixed convection. Rar=Kgrβb(Tw−T∞)/αbυbis the Rayleigh number for the porous medium. whereqr=−(4σ∗/3k∗)(∂T4/∂y) is the radiative heat flux.σ∗andk∗are the Stefan-Boltzmann factor and the average absorption coefficient,respectively. From the aforementioned equation it is viewed that the radiation effect is to reinforce the thermal diffusivity.whereRd= 4σ∗T3∞/k∗knfis the radiation parameter.It is worth mentioning here that the normal solve for heat equation,Eq.(10) without non-linear radiation impact can be gained from the foregoing equation which diminishes tou(∂θ/∂x)+v(∂θ/∂y) = (αnf/αb)(∂2θ/∂y2) and eliminates heat source. The subject boundary conditions (5) become: Here we assume thatue= sinx(see Refs.[30–31]).Incorporating Eq.(9a) and utilizing boundary-conditions(11),Eq.(9b) can be written as: To solve Eqs.(8)–(10) and (12) with the boundaryconditions (11) introduce the following variables: The equation of continuity is automatically achieved by identifying a stream functionψ(x,y),defines as:u=∂ψ/∂yandv=−(∂ψ/∂x).Replacing the variables (13)into Eqs.(10) and (12),we obtain: where with the boundary conditions: Atx ≈0,i.e.nearby the bottom stagnation-point of circular cylinder surface,Eqs.(14) and (15) diminish to the subsequent ordinary DEs: with the boundary conditions: where primes indicate toη-differentiation.The practical interest quantities,in the current investigation are the coefficient of skin frictionCfxand Nusselt numberNuxwhich are defined as: whereτwandqwdenote the surface shear stress and the local heat transfer coefficient.Substituting from Eqs.(7)and (13) into Eqs.(20) and (21),to gain the skin friction and reduced Nusselt number as: To resolve the problem formulated above by the DEs(17)–(18),with the boundary condition (19),we suppose that: The system of Eqs.(17) and (18) reduce to subject to The variation form coupled with Eqs.(24)–(25)over a standard linear two-nodded (ηe,ηe+1) is specified as: wherew1,w2,andw3are arbitrary functions inf,h,andθ. The model of finite element may be gained from Eqs.(27)–(29)by replacement approximations of finite element in the form: withw1=w2=w3=ψi(i= 1,2),whereψi’s are the functions of shape for a squaredelement(ηe,ηe+1)and are defined as: The finite element system of equations is: where [Kmn] and [bm] (m,n=1,2,3) are defined as: where, The same system after grouping of all the elemental equations is non-linear therefore an iterative technique is used in the solution,which is resolved by utilizing the Gaussian elimination technique with preserving an accuracy of 10−5. CNTs are cylindrical projectiles manufactured,in notion,by rolling graphene plates into a smooth cylinder.CNTs found in two types SWNTs or MWNTs.The SWNT composed of one graphene plate,whichis a flat benzene molecules matrix,including only hexagonal loops with single and double C-C bonding.The axis rolling selection relative to the graphene plate hexagonal grid and the closing cylinder radius provides for diverse kinds of SWNTs,which vary from insulating to conducting.Figure 2 depicts three various types of SWNTs:[32] Fig.2 (Color online) Schematic SWNTs structures. The impacts of NPs shapes in the existence of heat source/sink and radiation on the problem of MHD blood based on SWCNTs flow through a circular cylinder in horizontal position are analyzed and examined.The SWNTs shapes in SWNTs-blood play an important influence on temperature profiles.These three types of NPs shapes are illustrated in Fig.3.The numerical calculations of the thermo-physical characteristics of SWCNTs and blood are utilized from Table 1.In order to admit that our method is acceptable,it is agreed from Table 2 that the numerical result of the heat transfer rate−θ′(0) for diverse parameter of theλare associated with the results have been obtained by of Nazaret al.[30−31]and Cheng.[33]An ideal accord can be remarked among them.Table 3 introduces the calculated values of heat transfer rates−θ′(0) for diverseφ,λ,s,MandRdvalues with various NPs shapes.It is illustrated that the spherical NPs have a considerable effect in heat transfer rate generally,whereas the effects of governing parameters increase or decrease according to each parameter on−θ′(0).This will be discussed in the subsequent section. Fig.3 (Color online) NPs diverse shapes.[34] Table1 The fluid and NPs thermo-physical properties.[35] Table2 Comparison values of−θ′(0)whenφ=0(pure blood) andM =Rd =s=0 withλ. Figure 4 illustrated the NPs volume fraction effects ofφ(0.05≤φ ≤0.2) on the velocityf′(η) and temperatureθ(η) distributions for nanofluid (blood based on SWNTs)whenM= 0.1,λ=Rd= 1.0,ands= 0.1.It is remarkedthat for both cylindrical and lamina NPs shapes,as theφraises,the flow velocity and the nanofluid temperature diminish.The opposite trend takes place in the temperature profile withφin the case of spherical NPs.It is also observed that variations inφpoints to adaptations in nanofluid flow velocity and temperature which plays an important role in the cooling and heating procedures like,therapy of hematology diseases related to high body temperature.The effect of magnetic field parameterMon velocity and temperature distributions is illustrated in Fig.5 whenφ=0.05,λ=Rd=1.0,ands=0.5.It is noticed that for growing theMvalue,the velocity exceeds,on contrary the temperature.The magnetic fieldMhas powerful impacts on the flow velocityf′than on the temperatureθ.This result to a physical internal structure characterization of the nanofluid in motion with NPs shape,which is at the own time conformity with the Lorentz force.WhereasMdepends on porous parameterK,the porous medium resistance is scaled down which hikes the momentum enhancement of the nanofluid flow regime definitively develops the velocity field for both SWNTs shapes.Figure 6 detects the influence of the heat source parameterson flow velocity and profile of temperature whenφ= 0.05,λ=Rd= 1.0,M= 0.3.The nanofluid velocity and temperature profiles exceed(for all types of NPs shapes) with mounting valuessresulting to an increment in the boundary layer thickness of the velocity.Physically,the increasing temperature results to heat source,which is boosted NPs movement and therefore enhances the velocity of the nanofluid.In Fig.7,the distributions of velocity and temperature for diverse amounts of thermal radiation parameterRdare drawn whenφ=0.1,λ=1.0,s=0.5 andM=0.3.It is noted that for considerable values ofRd,flow velocity and temperature increase which interpret the physical status that asRdraises.The velocity and boundary-layer thickness of temperature tend to become more stable with increasing values ofRd. Table3 Values of−θ′(0)for diverseφ,λ,s,M andRd with different nanoparticle shapes Figure 8 exposes the effects of mixed convection parameterλon the fields of velocity and temperature atφ=0.1,Rd= 3.0,s= 1.0,andM= 0.3.The nanofluid velocity raises steadily with rising values ofλfor diverse SWNTs shapes.The opposite direction happens in temperature profile with increasingλ.Fundamentally,this is the result to the causing that a rise inλindicators to an increment in the porosity of the mediumKand other the fluid viscosityυbdiminishes.In cooled cylinder (λ <0),SWNTs spherical shape causes a disturbance in the flow velocity and temperature.This means that the flow is in the opposite trend or there is no flux whenλ <0 and SWNTs with spherical shape. Fig.4 (Color online)f′(η) andθ(η) viaφ for diverse NPs shape. Fig.5 (Color online)f′(η) andθ(η) viaM for diverse NPs shape. Fig.6 (Color online)f′(η) andθ(η) vias for diverse NPs shape. Fig.7 (Color online)f′(η) andθ(η) viaRd for diverse NPs shape. Fig.8 (Color online)f′(η) andθ(η) viaλ for diverse NPs shape. Figure 9 demonstrates the heat transfer rate difference for SWNTs shapes for miscellaneous NPs volume fractionφwithλwithRd=2.0,s=0.5,andM=0.1.It is monitored that with the rising of NPs promote heat transfer rate,except in the case of lamina shape.Depending onknf,the blood has declined heat transfer rate as compared with the blood based SWNTs.Lamina shape has a great impact when applied case of negative flow (i.e.opposing flowλ<0).Other,the growth values ofλincrease the rate of heat transfer.Likewise,Fig.10 describes the heat transfer differ with magnetic fieldMfor diverse shapes of NPs atφ= 0.05,Rd= 1.0,ands= 0.5.It is shown that heat transfer rate hikes result to enforcement of applied transverse magnetic field.This because magnetic field yields electric current in nanofluid which yields heat and hence the magnetic field enhances phenomena.Figure 11 the radiation effectRdon heat transfer rate−θ′(0)whenφ=0.1,M=0.3 ands=0.5.It is found displays that the risingRdraises transfer rate in opposing flow(λ <0) and reduces transfer rate in adding flow (λ >0)case.The impact of heat source or sinkson heat transfer rate is drawn in Fig.12.−θ′(0)diminishes with the rising values ofsatφ=0.1,Rd=1.0,andM=0.5.The lamina shape is the significant affect in the case of opposing flow,but in positive flow case (λ>0) the spherical shape is more efficient than others. Fig.9 (Color online)−θ′(0) viaλ withφ for diverse NPs shape. Fig.10 (Color online)−θ′(0) viaλ withM for diverse NPs shape. Fig.11 (Color online)−θ′(0)viaλ withRd for diverse NPs shape. Fig.12 (Color online)−θ′(0) viaλ withs for diverse NPs shape. The impacts of NPs shapes in the existence of radiation and heat source/sink on the problem of MHD.The SWNTs shapes in SWNTs – blood play an important influence on temperature profiles.The problem of MHD mixed convective nanofluid in the case blood based on SWCNTs flow through a circular cylinder are investigated numerically.Spherical,cylindrical and laminar NPs shapes in the presence of radiation and heat source or sink influences are analyzed.The flow velocity,temperature and rate of heat transfer inside the nanofluid with diverse NPs shapes are pointed in figures and tables terms with various parameters impacts and the computational outcomes are incorporated as follows: •The lamina shape (m=16.1576) of NPs in SWNTs– blood plays an overriding role on flow velocity and temperature profiles with diverse governing parameters in the case of adding flow,but the spherical shape is dominant in opposing flow. •The flow velocity increases with the increase of NPs volume fraction,magnetic field,heat source/sink and radiation. •The spherical shape of SWNTs gives rise to opposite effects on temperature profile with rise of NPs volume fraction,which boosts the temperature for all the other shapes. •The increasing of mixed parameter and magnetic field lead to an increasing in temperature,but the contrary happens with growing values of radiation and heat source. •The NPs spherical shape has dynamic accomplishments in adding flow (heated cylinder) enhancement over a heat transfer rate. •The existence of magnetic field and NPs volume fraction has more advisable enhancement on heat transfer as compared with the heat source and radiation for diverse NPs shapes. •In opposing flow (cooled cylinder),heat transfer declines significantly,especially with the spherical NPs shape and diminishes increasingly with heat source increment,which makes it an important application in the cooling processes. Conflicts of interest The authors announce that there is no conflict of interests about the publication of this article.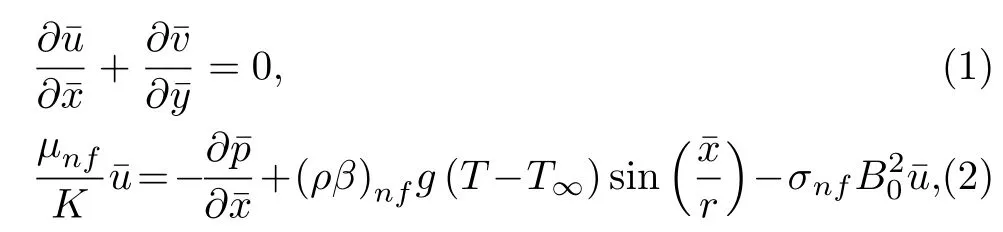


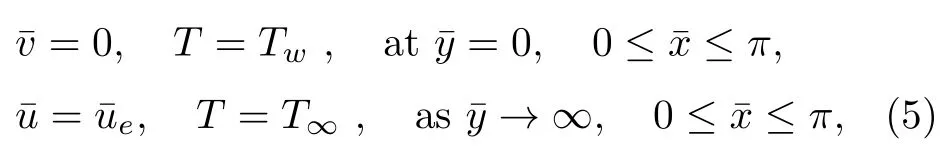
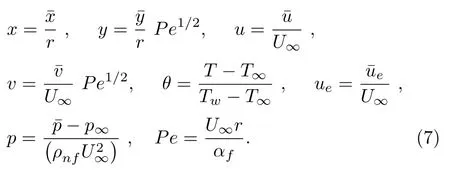

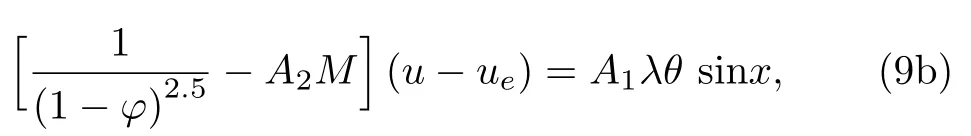
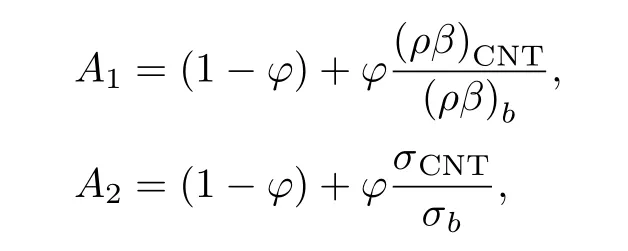
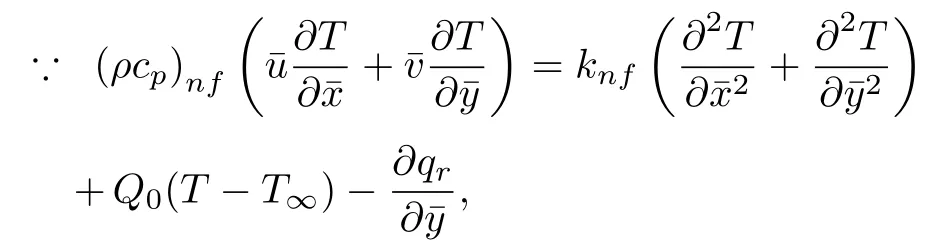

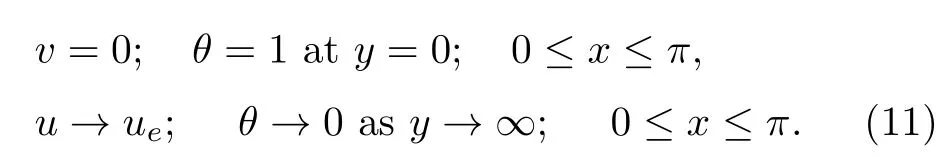


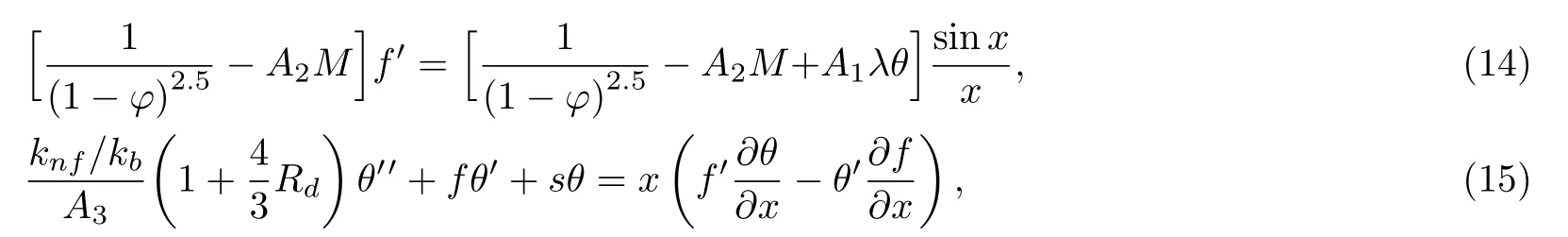
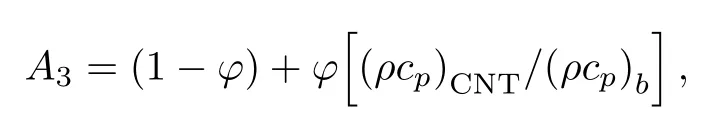
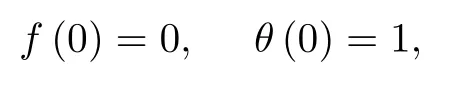
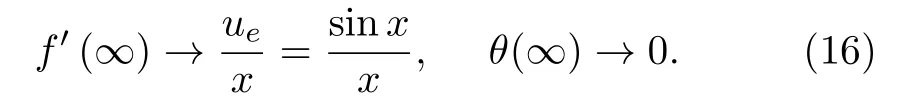
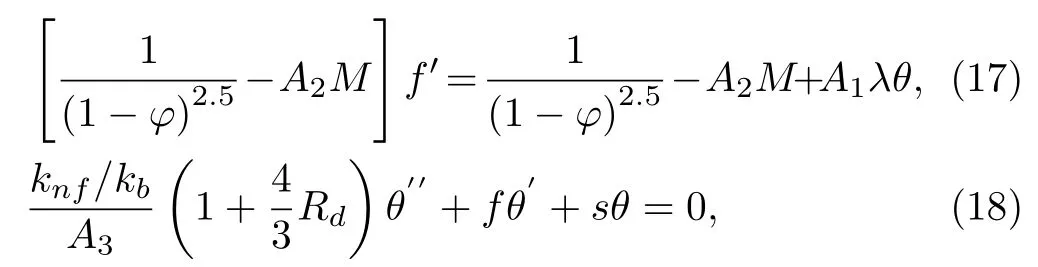
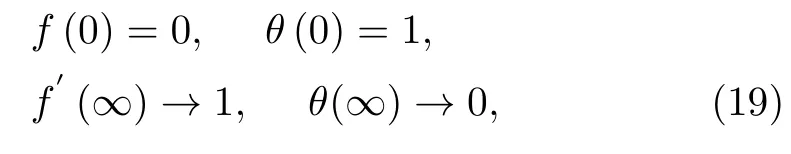
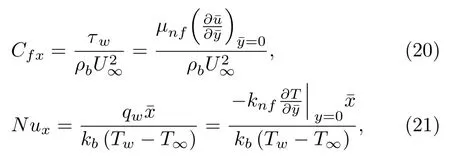

3 Solution Methodology
3.1 Finite Element Technique
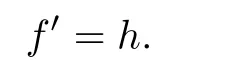


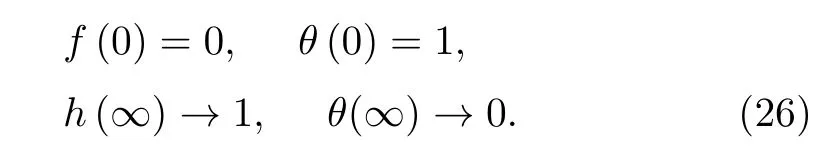
3.2 Formulation of Variation

3.3 Formulas of Finite Element



4 Discussion







5 Closing Remarks
杂志排行
Communications in Theoretical Physics的其它文章
- The Effects of Wettability on Primary Vortex and Secondary Flow in Three-Dimensional Rotating Fluid∗
- Periodic Orbits Around Kerr Sen Black Holes∗
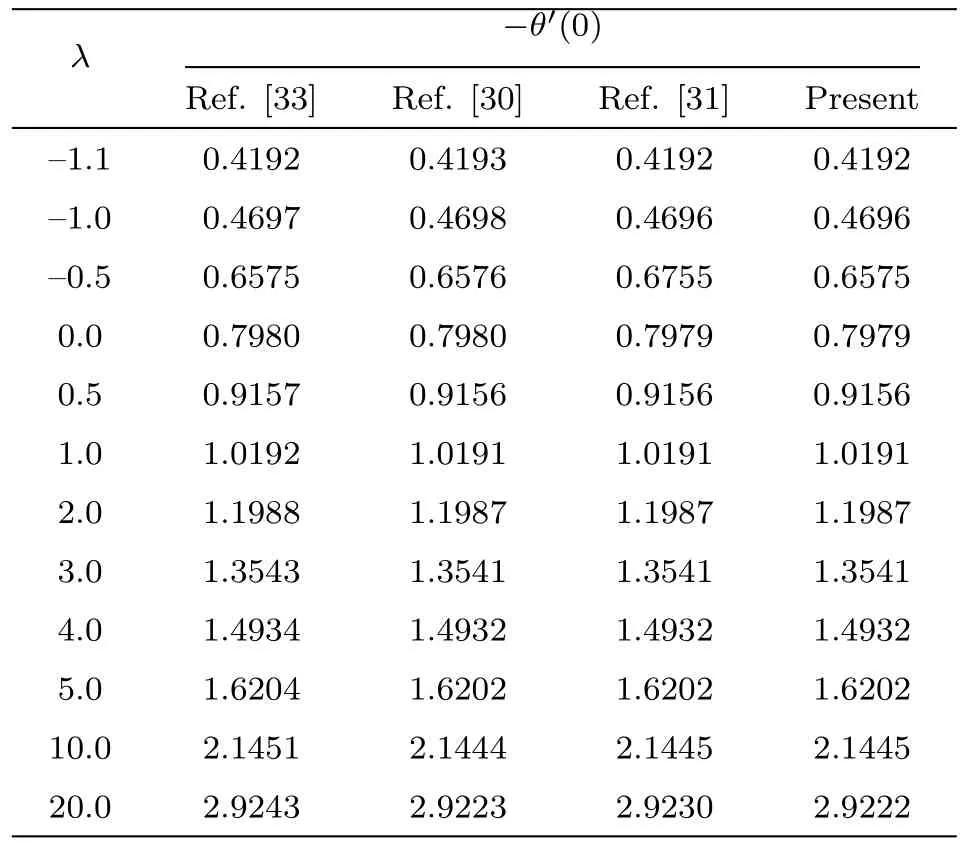
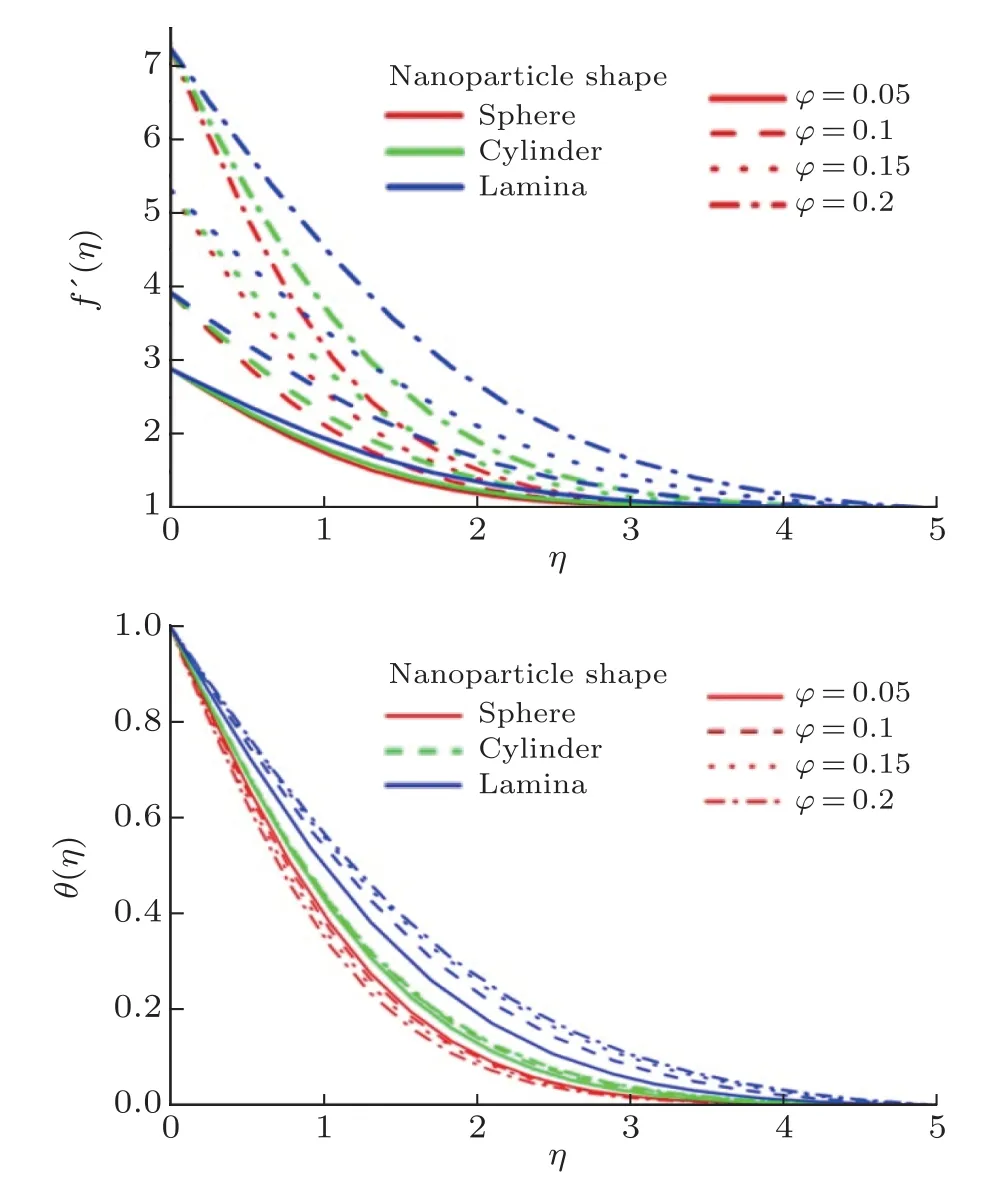
- Relativistic Self-Focusing of Hermite-cosh-Gaussian Laser Beam in Magnetoplasma with Exponential Plasma Density Ramp
- An Improved Heterogeneous Mean-Field Theory for the Ising Model on Complex Networks∗
- Parameterized Post-Post-Newtonian Light Propagation in the Field of One Spherically-Symmetric Body∗
- An Optimal Analysis for 3D Flow of Prandtl Nanofluid with Convectively Heated Surface
