Hydromagnetic Carreau Nanoliquid in Frames of Dissipation and Activation Energy

M.Waqas,Saira Naz, T.Hayat,, M.Ijaz Khan, and A.Alsaedi

1NUTECH School of Applied Sciences and Humanities,National University of Technology,Islamabad 44000,Pakistan

2Department of Mathematics,Quaid-I-Azam University 45320,Islamabad 44000,Pakistan

3Nonlinear Analysis and Applied Mathematics(NAAM)Research Group,Department of Mathematics,Faculty of Science,King Abdulaziz University,Jeddah 21589,Saudi Arabia

Abstract The novel characteristics of magnetic field and entropy generation in mixed convective flow of Carreau fluid towards a stretched surface are investigated.Buongiornio nanoliquid model consists of thermophoresis and Brownian movement aspects is opted for analysis.Energy expression is modeled subject to thermal radiation and viscous dissipation phenomenon.Concentration by zero mass flux condition is implemented.Consideration of chemical reaction and activation energy characterizes the mass transfer mechanism.Total entropy generation rate and Bejan number is formulated.The utilization of transformation variables reduces the PDEs into non-linear ODEs.The obtained nonlinear complex problems are computed numerically through Shooting scheme.The impact of involved variables like local Weissenberg number,magnetic parameter,thermal radiation parameter,Brownian motion parameter,thermophoresis parameter,buoyancy ratio parameter,mixed convection parameter,Prandtl parameter,Eckert number,Schmidt number,non-dimensional activation energy parameter,chemical reaction parameter,Brinkman number,dimensionless concentration ratio variable,diffusive variable and dimensionless temperature ratio variable on velocity,temperature,nanoparticles concentration,entropy generation,Bejan number,surface drag force and heat transfer rate are examined through graphs and tables.

Key words: carreau nanoliquid,entropy generation,viscous dissipation,activation energy,shooting scheme

1 Introduction

Nanoliquids are homogeneous dispersion of a carrier liquid and nanoparticles.The nanoparticles magnitude does not exceed 100 nm and their concentrations are normally small-scale (<10% by volume).The carrier liquids like oils,ethylene glycol and water have poor heat transport competence due to their low thermal conductivity.Choi[1]was the first who established nanoliquids.Such liquids have the capability to enhance thermal conductivity and thermal performance of carrier liquids.The heat transfer improvement can be modified by type of number of submerged nanoparticles,material and shape of particle.Nanoliquids have large-scale utilization in industrial and technological processes like nuclear reactor cooling,power generator,micro-reactors,melt-spinning,drying and cooling of papers,airplanes and glass fiber technology.Nanoliquids mechanism includes numerous factors such as thermophoretic force,thermal diffusion,micro-convection,particle to particle coupling,Brownian movement and conduction were investigated recently by several scientists.These scientists proved that nanoparticles Brownian movement is the leading factor that improves thermal characteristics and energy productivity of liquids.Some literature regarding nanoliquid flow have been studied (see Refs.[2–10]).

Non-Newtonian liquid flows have been widely utilized in the area of petroleum,chemical industries,biorheology and geophysics.Such liquids are highly complicated in nature as well as predicts non-linear relationship between shear stress and shear rate.A quantitative knowledge of flow characteristics of non-Newtonian liquids can not develop single constitutive mathematical relationship.Therefore,several non-Newtonian liquid models have been established to investigate their features.Here we consider the Carreau liquid model which exhibits the Newtonian/power law characteristics at low as well as high shear rates.In fact apparent viscosity increments at high shear rates to show shear thickening or dilatant features e.g.in biological liquids and polymer melts whereas apparent viscosity declines to behave as shear thinning features at high shear rates e.g.in concentrated suspensions of china and titanium dioxide.Boundary layer flow and heat transfer to Carreau liquid model towards a nonlinear stretching sheet is addressed by Khanet al.[11]Hayatet al.[12]reported the impacts of MHD and mixed convective flow in peristalsis of non-Newtonian nanomaterial considering zero mass flux condition.Hashimet al.[13]modeled anti-Fourier theory for Carreau liquid flow subject to slendering sheet.Hayatet al.[14]established numerical solutions of non-Newtonian liquid flows in the presence of chemical aspects.A numerical investigation for radiative MHD flow of Carreau nanoliquid model is delivered by Waqaset al.[15]Moreover magnetohydrodynamic flow of nanoliquids greatly attracted the consideration of numerous researchers due to their involvement in heat transfer performance and thermophysical characteristics.The behavior of fluid and heat transport characteristics are controlled by intensity and orientation of magnetic field.Furthermore valuable applications of magneto nanoliquid flow comprise elimination of tumors with hyperthermia,gastric medications,wound treatment,sterilized devices,asthma treatment and cancer therapy.Recent studies associated with magneto nanoliquid flow can be mentioned in the attempts.[16−21]

To enhance thermal performance and reducing irreversibilities in the system is thought to be an efficient approach.[22]The measured amount of heat transfer irreversibility and viscous dissipation irreversibility in a process is termed as entropy generation.The investigation on entropy generation has acquired the attention of researchers and investigators due to its extensive utilization in numerous systems such as microchannels,gas turbines,solar thermal,air separators,natural convection,curved pipes,reactors,regular and functionally graded materials,chillers,microchannels and so forth.[23−28]Entropy analyses enable us to determine how effective thermal process or system operates.[29−30]

To our knowledge mathematical modeling for Carreau nanoliquid with entropy generation minimization is not yet investigated.With this point of view our concern here is to model influence of nanoparticles in stretchable mixed convective flow of magneto Carreau liquid.The effects of viscous dissipation and thermal radiation are reported.Nanofluid modeling comprises the thermophoretic and Brownian movement aspects.Zero mass flux type boundary condition is imposed.Idea of activation energy along with chemical reaction is also introduced.Total entropy generation rate and Bejan number is discussed for various flow variables.By means of Shooting scheme,numeric solutions for nonlinear systems are constructed.Nature of emerging physical variables on velocity,temperature,concentration,surface drag force,local Nusselt number,entropy generation and Bejan number are analyzed through graphs and tables.

2 Formulation

Entropy generation minimization and magnetohydrodynamic (MHD) mixed convective flow of an incompressible carreau nanoliquid bounded by stretchable surface is considered.Coordinate system is taken in such a way thatx-axis is in the direction of stretchable surface whereasyaxis is perpendicular to it (see Fig.1).Features of Brownian motion and thermophoresis in nanoliquid modeling are examined.Viscous dissipation and thermal radiation aspects in energy expression are acounted.Besides,binary chemical reaction with Arrhenius activation energy are retained.The boundary layer approximation yields the following expressions:

with

Here(u,v)represents the velocity components in(x,y)direction,ρfthe density of fluid,ν(=µ/ρf) the kinematic viscosity of the fluid,µthe dynamic viscosity,Γ the material constant,B0the uniform magnetic field strength,τ(= (ρc)p/(ρc)f) the ratio of heat capacity with (ρc)fthe heat capacity of fluid and (ρc)pthe effective heat capacity of nanoparticles,σ∗∗the Stefan-Boltzmann constant,α(=kf/(ρcp)f)the thermal diffusivity,kfthe thermal conductivity of the fluid,cpthe specific heat capacity,m∗the mean absorption coefficient,σ∗the electrical conductivity,(DB,DT) the (Brownian,thermophoresis)diffusion coefficients,(T,C)the(temperature,concentration),(T∞,C∞) the ambient (temperature,concentration),(Tw,Cw) the surface (temperature,concentration),κ= 8.61×10−5eV/K the Boltzmann constant,k2rthe reaction rate,Eathe activation energy,mthe fitted rate constant,cthe dimensional constant,Uw(x)the stretching velocity.

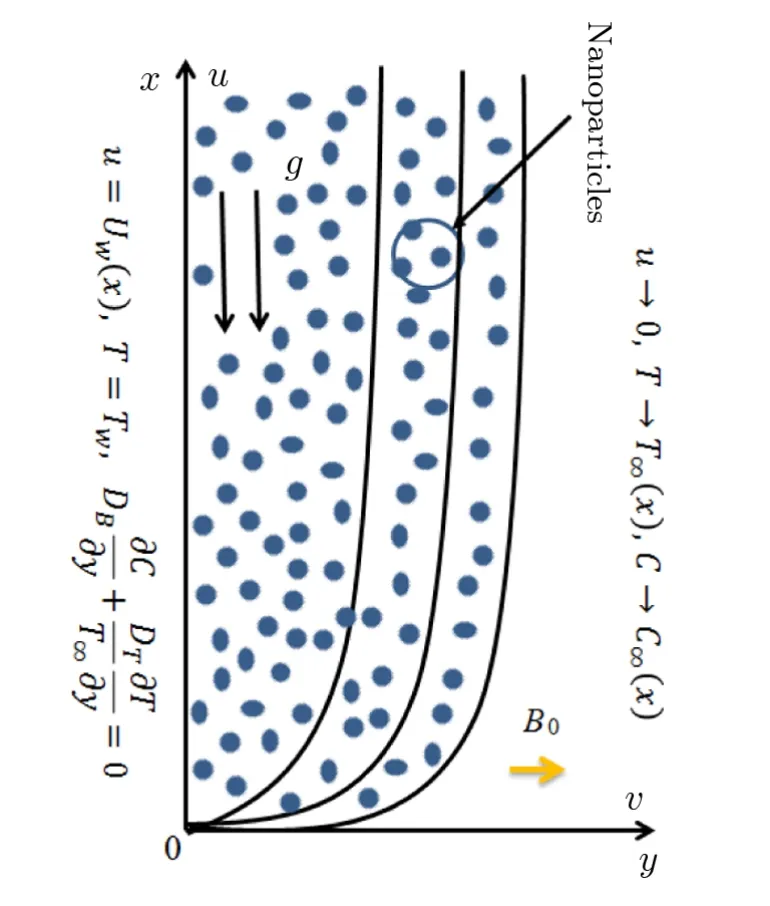
Fig.1 (Color online) Physical configuration.

We utilize the transformations[31−32]

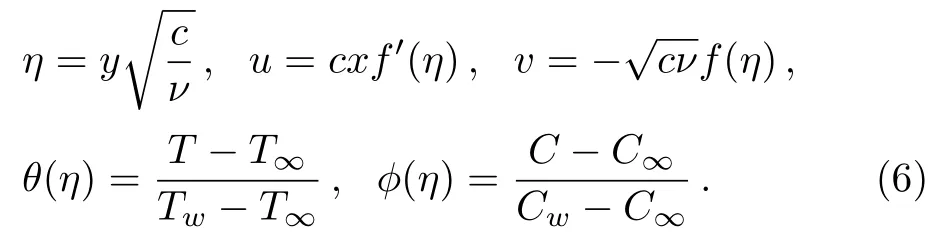
Heref′(η),θ(η),andϕ(η)depict the non-dimensionalized velocity,temperature and concentration.

Equation (1) is satisfied identically foru=cxf′(η),utilizing expression (6) into the expressions (2)–(5),we get the differential systems as follows:

where prime (′) denotes differentiation with respect toη,M(=σ∗B20/ρfc) the magnetic parameter,

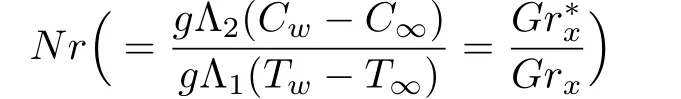
the buoyancy ratio parameter,

the mixed convection parameter,Pr=ν/αthe Prandtl number,R= 4σ∗∗T3∞/kfm∗the thermal radiation parameter,Nb=τDB(Cw−C∞)/νthe Brownian motion parameter,Nt=τDT(Tw−T∞)/νT∞the thermophoresis parameter,Ec=c2x2/cf(Tw−T∞) the Eckert number,We2= Γ2c3x2/νthe local Weissenberg number,Sc=ν/DBthe Schmidt number,σ=kr2/cthe dimensionless reaction rate,E=Ea/κT∞the dimensionless activation energy,δ1= (Tw−T∞)/T∞the temperature difference parameter.

Physial Quantities

We have the following expressions for the drag force(Cfx) and local Nusselt number (Nux):

where the (τw,qw) represents the (wall shear stress,wall heat flux) which are given by:

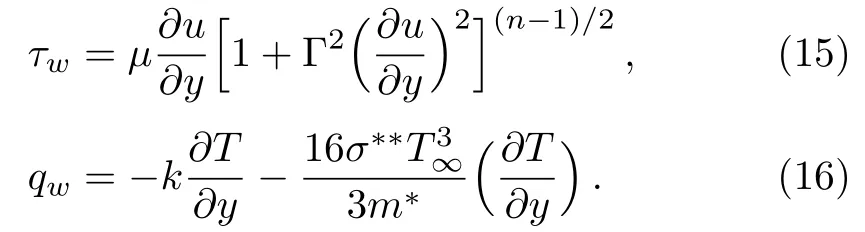
Substituting Eqs.(15)and(16)in Eqs.(13)–(14),we have following dimensionless forms of surface drag force and local Nusselt number:

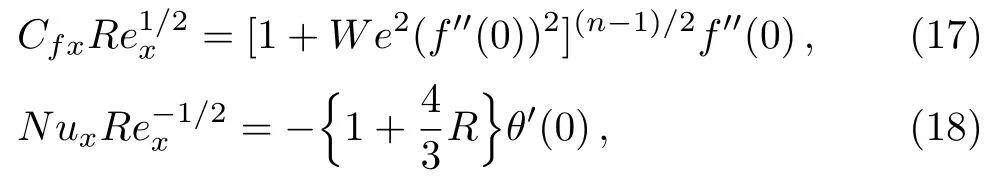
whereRex(=xUw/ν) signifies local Reynolds number.

3 Analysis of Entropy Generation

The chaos in a particular system is computed through entropy.Entropy generation relies on reversibility of the process.In isolated structures,entropy rises subjected to time for irreversible reactions.Owing to an increase in utilization of nanoliquids in medical and engineering applications,it is essential to examine and comprehend the influence of these nanoliquids versus entropy generation in real mechanisms.[33]

For carreau liquid flow the volumetric entropy generation equation in dimensional form is defined as:

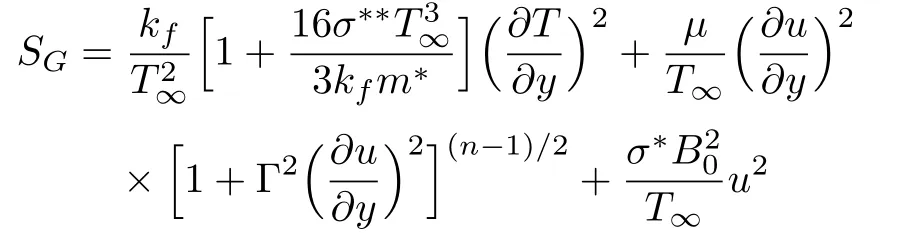
Here the above expression constitutes three factors (i)fluid friction irreversibility,(ii) heat transfer irreversibility,and (iii) diffusive irreversibility.After employing the similarity transformation,Eq.(19) can be reduced into dimensionless form as follows:

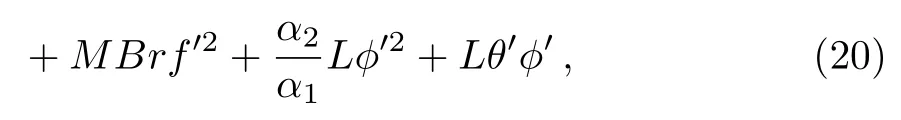
whereNG(=νT∞SG/kfc∆T) depicts the entropy generation rate,Br(=µU2w/kf∆T) the Brinkman number,α2(=∆C/C∞)the dimensionless concentration ratio variable,α1(= ∆T/T∞) the dimensionless temperature ratio variable,L(=RD(Cw−C∞)/kf) the diffusive variable.

The Bejan number (Be) is defined as

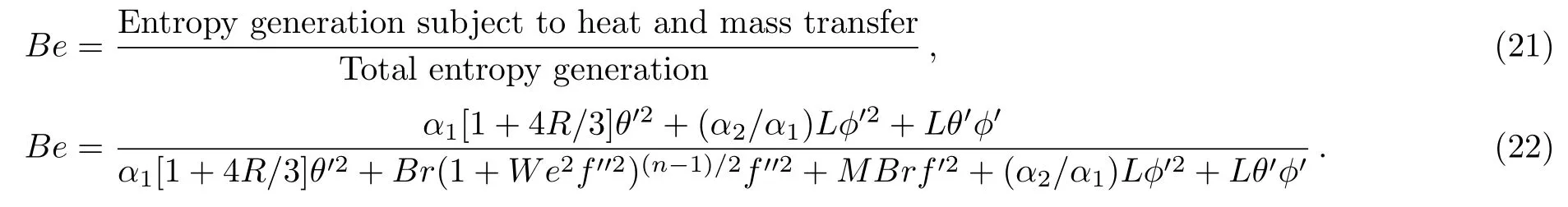
4 Results and Discussion

Here Shooting scheme is implemented to compute the nonlinear systems (7)–(9) subject to Eqs.(10)–(12) and(20)–(22).Salient features of emerging variables such as magnetic parameter (M),local Weissenberg number(We),thermal radiation parameter (R),Buoyancy ratio parameter (Nr),Brownian motion parameter (Nb),thermophoresis parameter (Nt),mixed convection parameter(λ),Prandtl parameter (Pr),Eckert number (Ec),nondimensional activation energy parameter(E),chemical reaction parameter(σ),Schmidt number(Sc),entropy generation rate (NG),Brinkman number (Br),dimensionless concentration ratio variable (α2),dimensionless temperature ratio variable (α1) and diffusive variable (L) on velocityf′(η),temperatureθ(η),concentration of nanomaterialsϕ(η),entropy generation (NG) and Bejan number(Be) are scrutinized through graphs in this section.This objective is achieved through illustration of Figs.2–27.These figures are shown for both shear thickening (n>1)and shear thinning (n <1) cases.The impact ofMonf′is presented in Fig.2.Heref′decays via largerM.The liquid velocity is much smaller in hydromagnetic case when compared with hydrodynamic case.It is due to the fact that Lorentz force becomes stronger when increments inM.Therefore stronger Lorentz force create resistance to transport phenomenon which is accountable for diminishment in the velocityf′.The curve off′for values ofλis investigated in Fig.3.We noticed an improvement inf′subject to largerλ.Physically enhancement in buoyancy forces yields higher liquid velocity.Analysis of features ofNronf′is addressed in Fig.4.Heref′is increasing function of largerNr.Figure 5 reveals the impact ofWeonf′.Heref′enhances via largerWefor shear thickening liquid whereas decays for shear thinning liquid.Figure 6 interpretsθvariation forEc.Hereθaugments whenEcis incremented.The relation between the flow of enthalpy difference and kinetic energy is called Eckert number.It elaborates change of kinetic energy into internal energy by work done versus the viscous liquid stresses.The larger Eckert numberEccauses loss of heat from the plate to the liquid i.e.cooling of the plate.In other words larger energy dissipation produces higher liquid temperature.

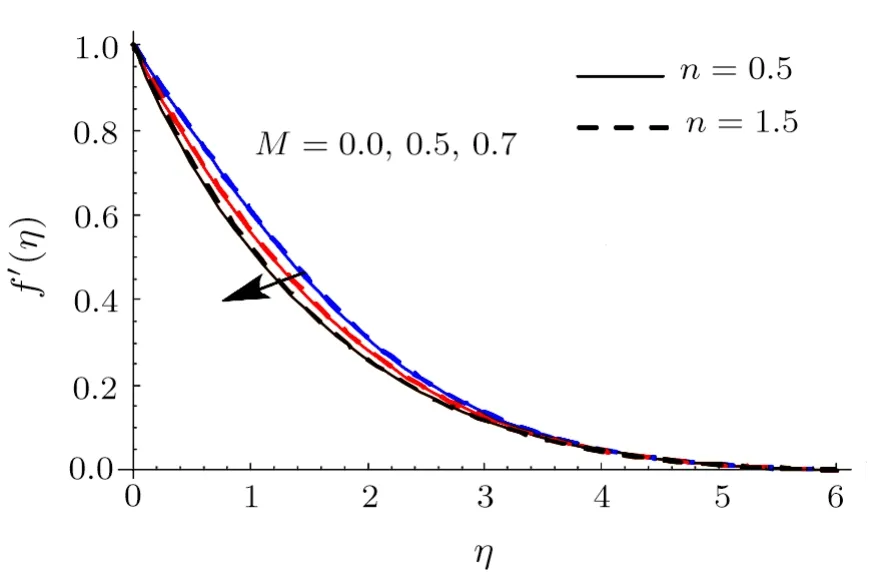
Fig.2 (Color online)f′ impact for differentM.

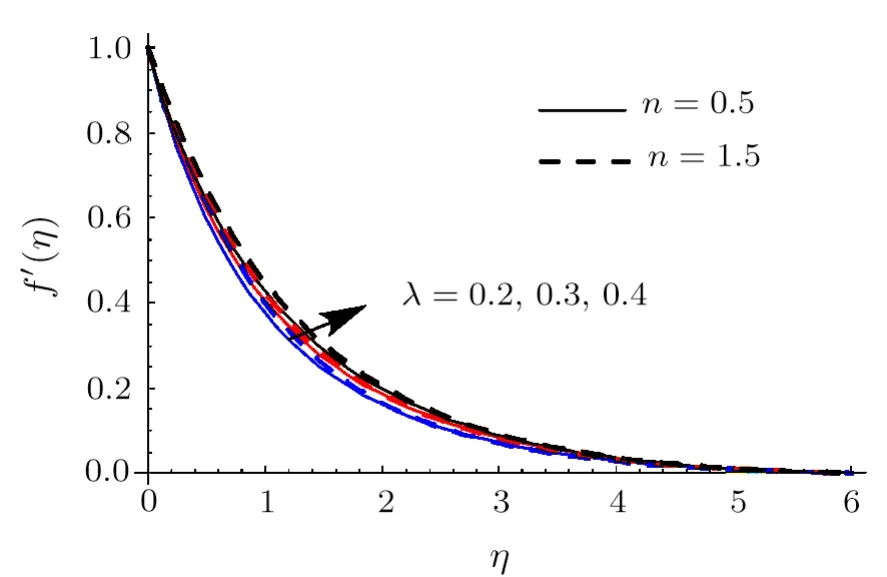
Fig.3 (Color online)f′ impact for differentλ.

Figure 7 portrays the impact ofNtonθ.Clearly largerNtyields higherθ.Physically small number of particles are pulled away from hot region to cold one in thermophoresis phenomenon.Hence large number of nanomaterials are moved away from the heated region which inflates the liquid temperature.Features ofPronθare exhibited in Fig.8.Hereθdecays whenPris incremented.In fact largerPrreduces the thermal diffusivity which accordingly decay liquid temperature.The role ofRonθis explored in Fig.9.

Fig.4 (Color online)f′ impact for differentNr.

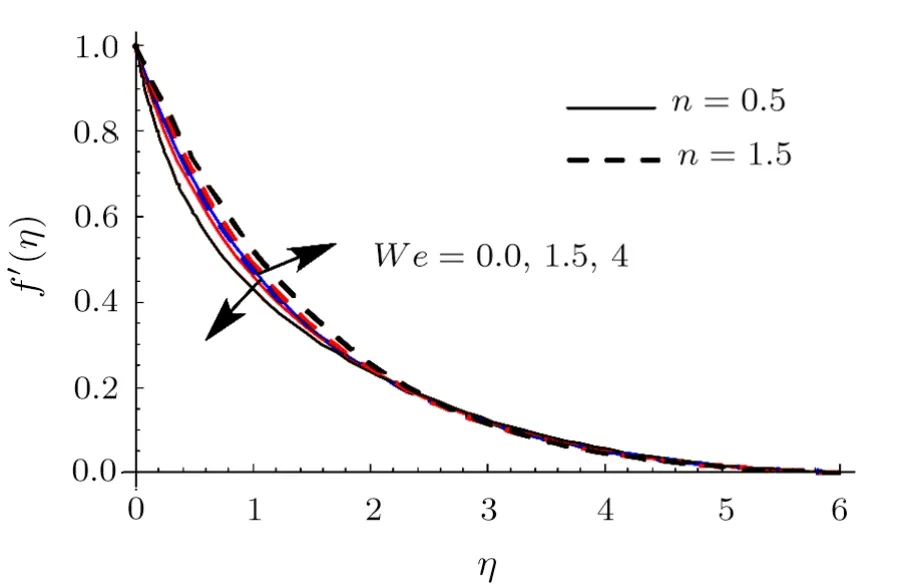
Fig.5 (Color online)f′ impact for differentWe.

Fig.6 (Color online)θ impact for differentEc.

Fig.7 (Color online)θ impact for differentNt.

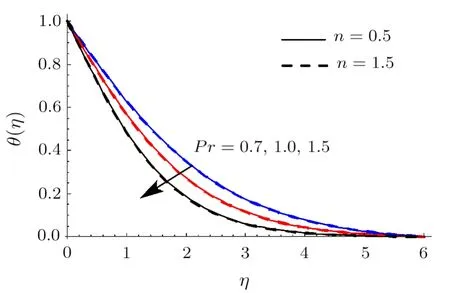
Fig.8 (Color online)θ impact for differentPr.

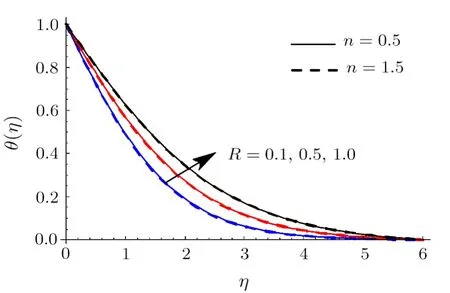
Fig.9 (Color online)θ impact for differentR.

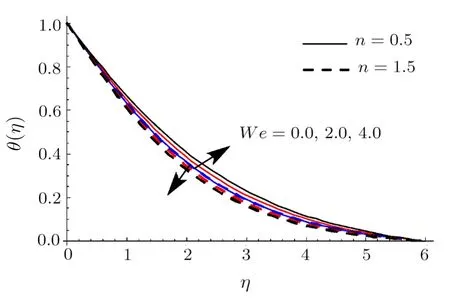
Fig.10 (Color online)θ impact for differentWe.

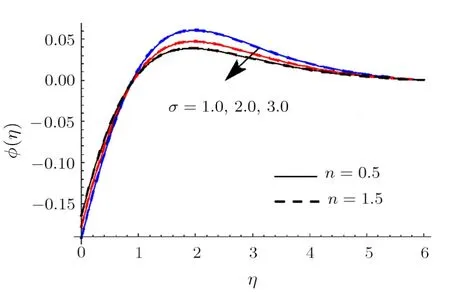
Fig.11 (Color online)ϕ impact for differentσ.

Fig.12 (Color online)ϕ impact for differentSc.

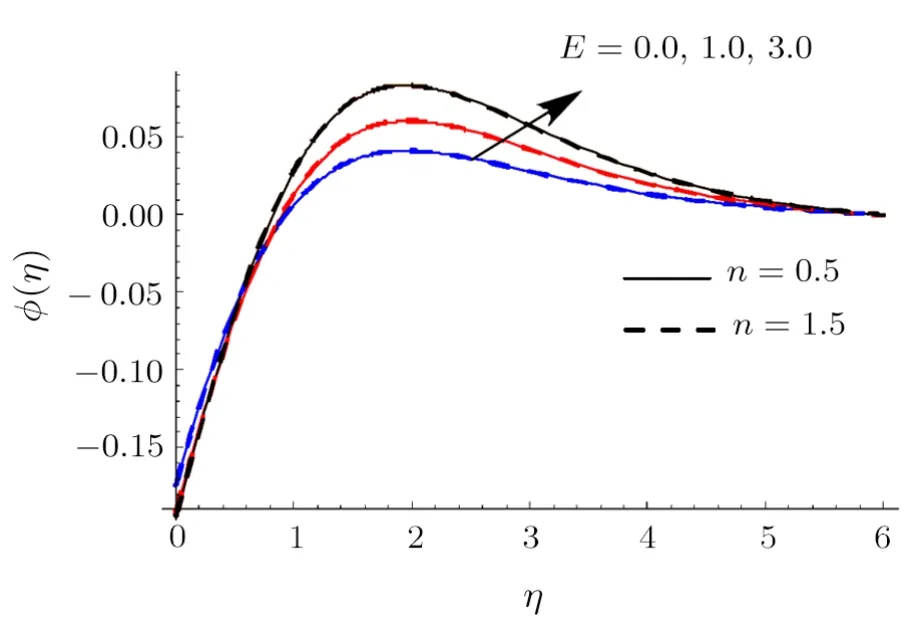
Fig.13 (Color online)ϕ impact for differentE.

Fig.14 (Color online)ϕ impact for differentNb.

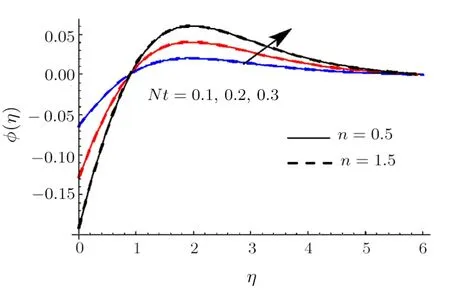
Fig.15 (Color online)ϕ impact for differentNt.

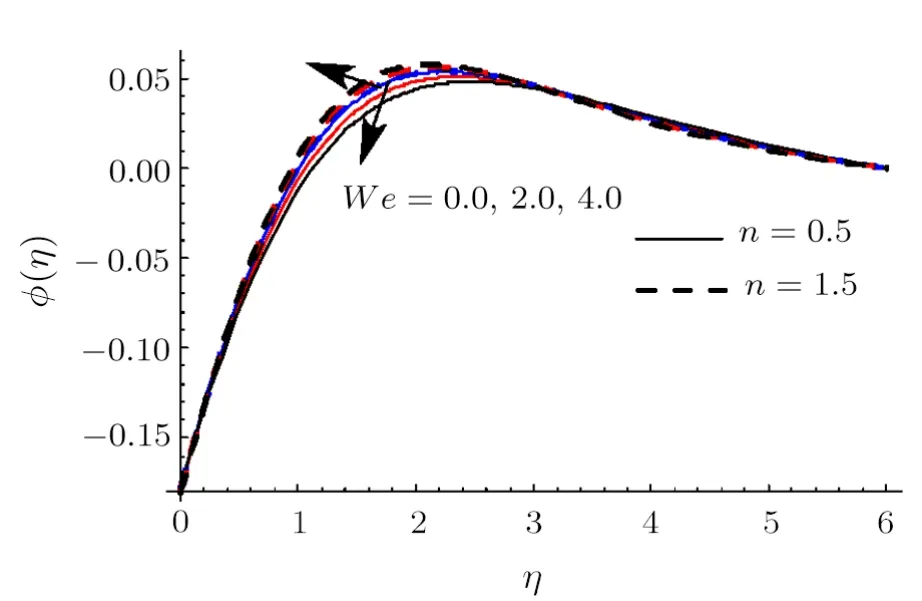
Fig.16 (Color online)ϕ impact for differentWe.

Clearly rise inRaugmentsθ.Physically radiation process produce more heat in the working liquid thereforeθand related thermal layer thickness enhances.Influence ofWeonθis reported in Fig.10.Hereθincrements via larger ofWefor shear thinning liquid (i.e.n <1) and consequently thermal layer thickness escalates.Moreoverθhas opposite characteristic for higher estimationWefor shear thickening liquid (i.e.n >1).Figure 11 is plotted to examine the impact ofσonϕ.we observed thatϕenhances for higher estimation ofσ.Actually consumption of reactive species decays rapidly for largerσ.Thereforeϕreduces.Feature ofSconϕare illustrated in Fig.12.Clearlyϕis reduced via largerSc.AsScis the ratio between momentum diffusivity to Brownian diffusion coefficient.Brownian diffusion coefficient decays via largerScdue to whichϕand its related nanoparticles concentration layer diminishes.Figure 13 depicts the behavior ofEonϕ.It is examined that the term exp(−Ea/κT) decreases for higher estimation ofEa.This eventually generates chemical reaction due to whichϕimproves.The impacts ofNtandNbonϕare interpreted in Figs.14 and 15.For largerNt,ϕand thickness of nanoparticles concentration boundary layer escalates.Actually thermophoretic force increases for higher estimation ofNtdue to which nanoparticles moves from higher to lower temperature andϕboosts up (see Fig.14).Moreoverϕand its associated concentration layer reduce whenNbis incremented (See Fig.15).Figure 16 reportsWeoutcome againstϕ.Hereϕdecays via largerWefor shear thinning liquid (i.e.n<1)and nanoparticles concentration boundary layer thickness enhances.Furthermore opposite characteristic is noticed for shear thickening liquid (i.e.n>1).

4.1 Entropy Generation Rate and Bejan Number

Figures 17 and 18 depict the salient features ofBronNGandBe.In fact Brinkman numberBrhas characteristic to propagate heat by viscous flowing liquid to heat transport through molecular conduction e.g.in polymer processing.Heat transport via molecular conduction is much greater than heat propagation via viscous effects.Consequently movement of liquid particles generates more heat between the adjacent layers.It enhances the entropy and system disorderness (see Fig.17).Figure 18 displays thatBedecays via largerBr.It is due to the fact that largerBrcorresponds to increase in entropy rate which decays theBe.Figure 19 reports the impact ofLonNG.ClearlyNGshows decreasing trend forL.Figures 20 and 21 disclose the characteristics ofMonNGandBe.Here it is noticed thatNGaugments whenMis incremented.Physically rise inMcreates greater Lorentz force due to which resistance in liquid flow increases andNGenhances(see Fig.20).LargerMcorresponds to reduction inBe.It means that liquid friction irreversibility has dominating impacts over heat and mass transport irreversibility and consequentlyBedecays (see Fig.21).

Fig.18 (Color online)Be impact for differentBr.

Fig.19 (Color online)NG impact for differentL.

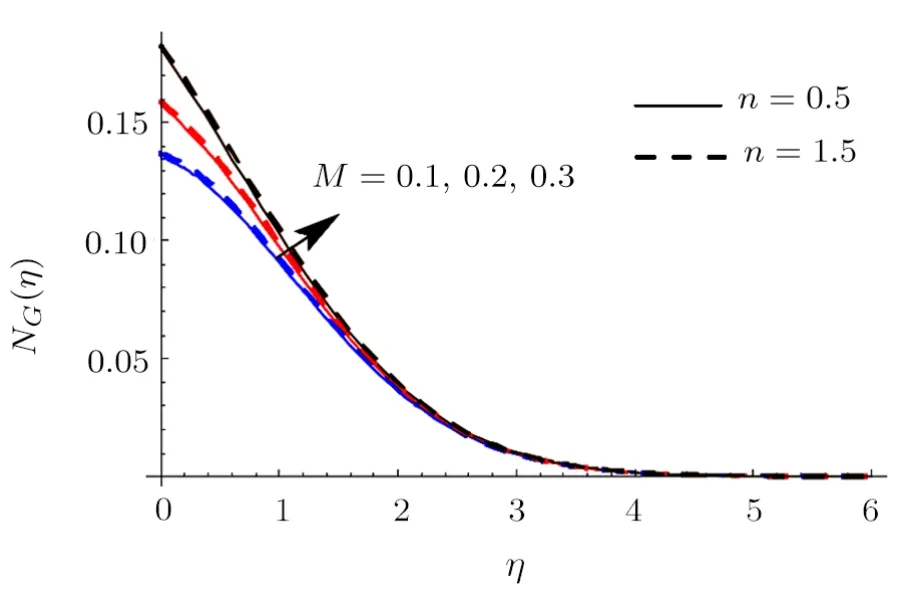
Fig.20 (Color online)NG impact for differentM.

Fig.21 (Color online)Be impact for differentM.

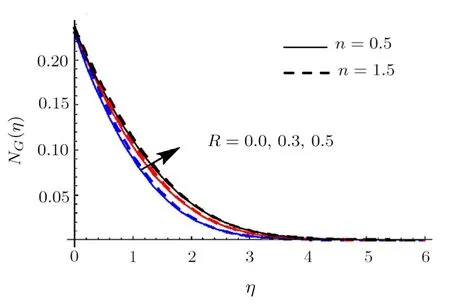
Fig.22 (Color online)NG impact for differentR.

Fig.23 (Color online)Be impact for differentR.

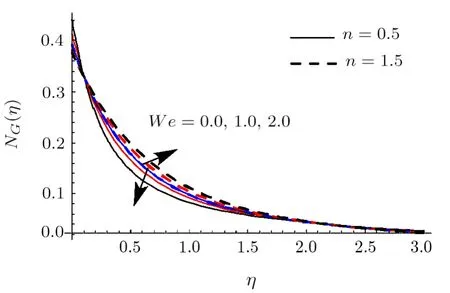
Fig.24 (Color online)NG impact for differentWe.

Fig.25 (Color online)NG impact for differentNb.

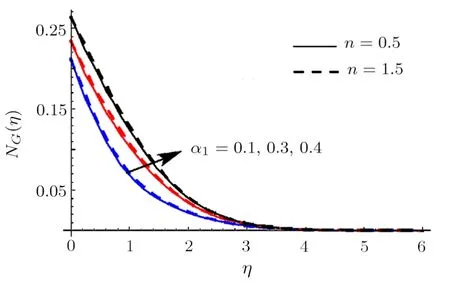
Fig.26 (Color online)NG impact for differentα1.

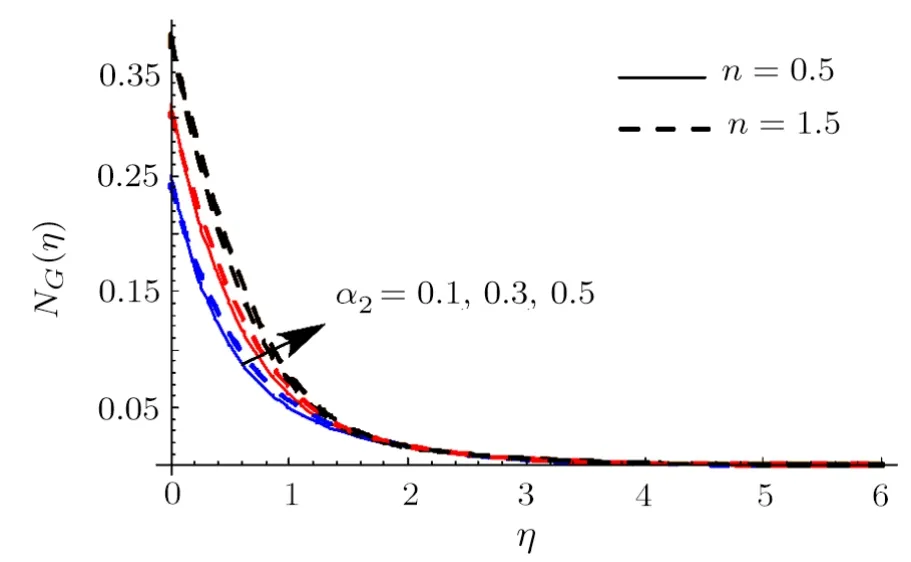
Fig.27 (Color online)NG impact for differentα2.

Figures 22 and 23 reveal the impact ofRonNGandBe.HereNGandBeenhance whenRis incremented.Physically increase in internal energy is responsible for an enhancement inNG.Actually heat and mass transport irreversibility has dominating impacts on liquid friction irreversibility.Salient features ofWeforNGare discussed in Fig.24.HereNGis enhanced for shear thickening case(i.e.n >1) whereas opposite scenario is noted for shear thinning case (i.e.n<1).Impact ofNbonNGis demonstrated in Fig.25.LargerNbcorresponds to decreasing trend in entropy generationNG.Figure 26 illustrates the characteristics ofα1onNG.HereNGenhances via largerα1.Physically liquid temperature increases for largerα1which accordingly enhances entropy generation rate.The curve ofα2onNGis displayed in Fig.27.It is evaluated that liquid concentration increases whenα2is incremented and consequentlyNGenhances.Moreover surface drag force diminishes for higher estimationHa.

4.2 Characteristics of Surface Drag Force and Heat Transfer Rate

Table1 portrays the influences ofHaandWeon surface drag force for both shear thinning and shear thickening cases.Here surface drag force enhances via largerWefor shear thinning liquid while it reduces for shear thickening liquid.

Table1 Surface drag forceCfxRe1/2x via different estimation ofWe andHa whenEc=Nr =0.1,Nt=0.3,Nb =R = 0.5,Pr = 1,Sc = 1,m = 0.3,σ =λ = 1,E =1,δ1 =0.2.

Table2 Heat transfer rateNuxRe−1/2x via different estimation ofEc,Pr,We,Nt,andR whenNr = 0.1,Nb=0.5,Sc=1,m=0.3,σ =λ=1,E =1,δ1 =0.2.

Table 2 points out the features of several embedded physical parameters on heat transfer rate.It is examined that heat transfer rate increases via largerPrandRwhereas it decays for largerEcandNt.

5 Conclusions

Entropy generation in MHD mixed convective flow of Carreau nanoliquid is investigated numerically in the presence of viscous dissipation and thermal radiation.The key points observed from the flow analysis are as follows:

(i) Liquid velocity retards the flow via larger magnetic parameter for both shear thickening/thinning case.

(ii) Velocity is increasing function of larger local Weissenberg number for shear thickening liquid in comparison to shear thinning liquid.

(iii) Increments in thermal radiation parameter increases the liquid temperature.

(iv) Thermal and nanoparticle concentration boundary layers are boosted via larger thermophoretic parameter.

(v) Stronger magnetic variable leads to higher entropy generation rate while decays for Bejan number.

(vi) Opposite scenario is observed for nanoparticles volume fraction through activation energy and chemical reaction rate.

(vii) Larger Brinkman gives rise to entropy generation rate in comparison to Bejan number.

(viii) Surface drag force reduces for larger magnetic parameter.

(ix) Heat transfer rate enhances via larger Prandtl number and radiative parameter when compared with Eckert number and thermophoretic parameter.

(x) Viscous nanoliquid situation can be retrieved by settingWe=n=0.