An Integrable Matrix Camassa-Holm Equation∗
2020-01-09LiFengChan产丽凤BaoQiangXia夏保强andRuGuangZhou周汝光
Li-Feng Chan (产丽凤), Bao-Qiang Xia (夏保强), and Ru-Guang Zhou (周汝光)
1Kewen College,Jiangsu Normal University,Xuzhou 221116,China
2School of Mathematics and Statistics,Jiangsu Normal University,Xuzhou 221116,China
Abstract We present an integrable sl(2)-matrix Camassa-Holm (CH) equation.The integrability means that the equation possesses zero-curvature representation and infinitely many conservation laws.This equation includes two undetermined functions,which satisfy a system of constraint conditions and may be reduced to a lot of known multicomponent peakon equations.We find a method to construct constraint condition and thus obtain many novel matrix CH equations.For the trivial reduction matrix CH equation we construct its N-peakon solutions.
Key words: Camassa-Holm equation,zero-curvature representation,conservation laws,N-Peakon
1 Introduction
In 1993,Camassa and Holm derived the following shallow water wave model[1]
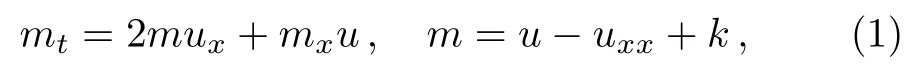
wherekis an arbitrary constant.This equation was referred to as the Camassa-Holm (CH) equation nowadays and it has attracted much attention in recent years.The CH equation was first implicitly included in the work of Fuchssteiner and Fokas[2]as a very special case.Since the work of Camassa and Holm,[1]various studies on this equation have remarkably been developed; see,for example,Refs.[3–6]and references therein.The most attractive feature of the CH equation is that,in the casek= 0,it admits peaked soliton (peakon) solutions.Such solutions are of great research interest and have been extensively studied from different points of view.In addition to the CH equation,other integrable models that admit peakon solutions have been found,such as the Degasperis-Procesi(DP) equation,[7]the modified CH equation,[8−10]the Novikov’s cubic nonlinear equation,[11]and some multicomponent extensions of CH equation.[12−21]
In this paper,we propose the following matrix CH-type equation
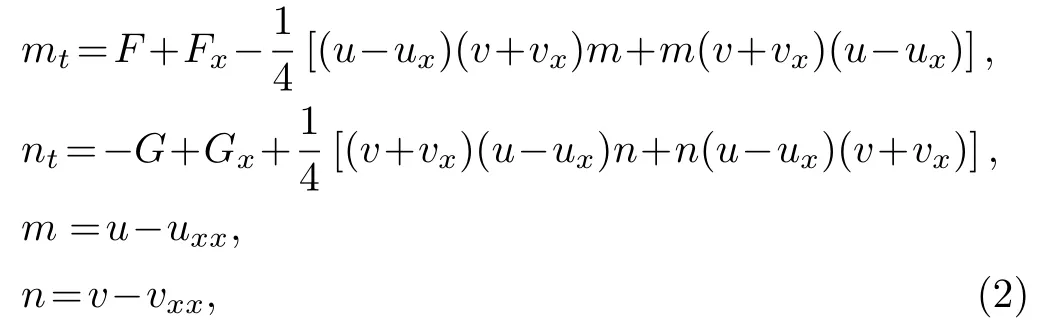
whereu,v,m,andnaresl(2)-valued matrices

FandGaresl(2) matrix valued functions whose entries are smooth functions ofujk,vjk,j,k=1,2 and their dervatives,and they satisfy the following constraints:
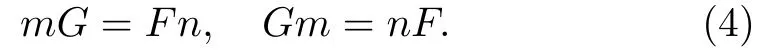
Equation (2) is actually a matrix extension of a family of two-component peakon equations proposed in Ref.[20](see Eq.(7) in Ref.[20]).By choosing appropriateFandGthat satisfy Eq.(4),we can recover several known integrable peakon models as well as some new peakon models as special cases of Eq.(2).For example,if we chooseu11=v11=0,u21=v21=2,u12=v12,and
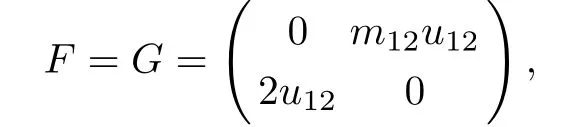
then Eq.(2) is reduced to the celebrated CH Eq.(1).If we chooseu12=v12=u21=v21=0,u11=v11,and
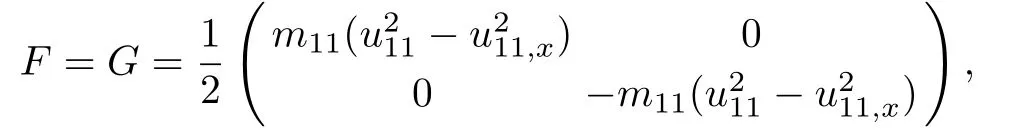
then Eq.(2) is reduced to the modified CH equation presented in Refs.[8–10].If we choose
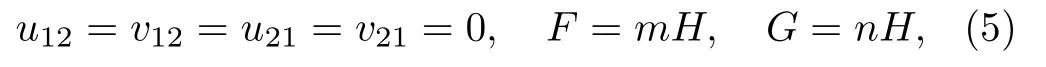
withHbeing an arbitrary function ofu11,v11and their derivatives,then Eq.(2) is reduced to a family of twocomponent peakon equations proposed in Ref.[20] (see Eq.(7) in Ref.[20]).Furthermore,we recover theU(1)-invariant peakon equations presented in Refs.[22–23]from Eq.(2) by imposing the complex conjugate reductionv11=u∗11on the reduction (5) with special choices ofH(see Refs.[19–20] for details).
In this paper,we show that Eq.(2) admits Lax representation and possesses infinitely many conservation laws.We also derive theN-peakon solutions for a new matrix CH-type equation containing in the matrix CH equation(2) as special cases.
The whole paper is organized as follows.In Sec.2,we present the Lax pair and conservation laws for Eq.(2).In Sec.3,we discuss theN-peakon solutions for a new matrix CH-type equations containing in the matrix CH Eq.(2).
2 Zero-Curvature Representation and Conservation Laws
Let thesl(2) valued matricesm,n,u,vbe defined by Eq.(3).LetFandGbe 2×2 matrix valued functions such that their entries are smooth functions ofujk,vjk,j,k= 1,2,and their dervatives,and they subject to the constraints (4).We introduce the matricesUandVas follows:
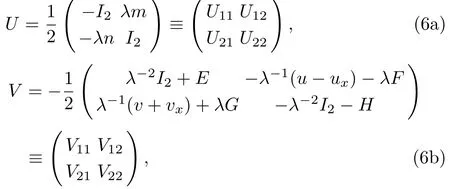
whereλis a spectral parameter,I2is the 2×2 identity matrix,and the matrix functionsE,Hare given by
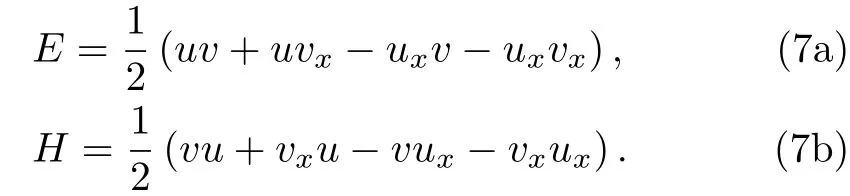
Consider a pair of linear spectral problems
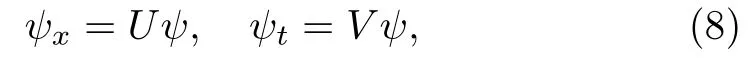
whereUandVare defined by Eqs.(6a) and (6b).The compatibility condition of Eq.(8),namely the zerocurvature representation generates

Substituting the expressions ofUandVinto Eq.(9)and recalling thatFandGsatisfy Eq.(4),we find that(9)is nothing but the matrix equation(2).Hence,Eq.(8)exactly gives the 4×4 matrix Lax pair of Eq.(2).
Next,let us construct conservation laws of Eq.(2).
We write Eq.(8) in the form
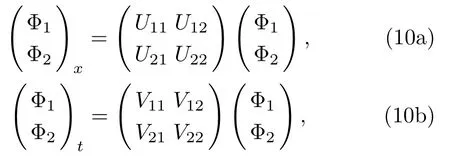
where Φ1,Φ2,UijandVij,1≤i,j ≤2,are 2×2 matrices.Letω= Φ2Φ−11.From Eq.(10a),we findωsatisfies the following matrix Riccati equation
From Eqs.(6a),(6b),and (10),we find
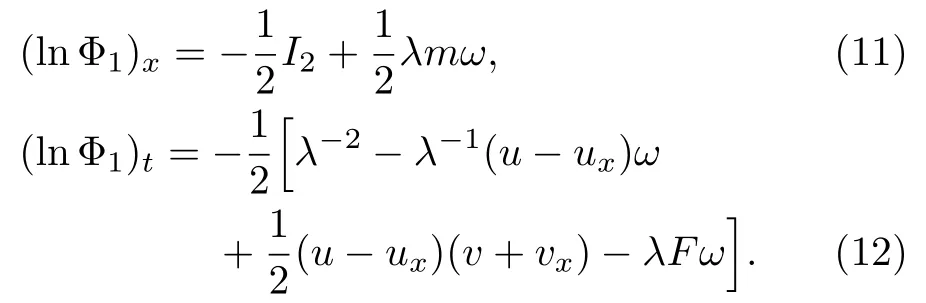
Equations (11) and (12) yield the following conservation law of Eq.(2):

where

Usually,ρandAare called a conserved density and an associated flux,respectively.
Equation(14)implies thatmωis a generating function of the conserved densities.We may derive explicit forms of the conserved densities by expandingωin the positive powers ofλ,

Substituting Eq.(16) into Eq.(11) and comparing powers ofλ,we find
By inserting Eqs.(16) and (17) into Eqs.(14) and (15),we finally obtain the following infinitely many conserved densities and the associated fluxes
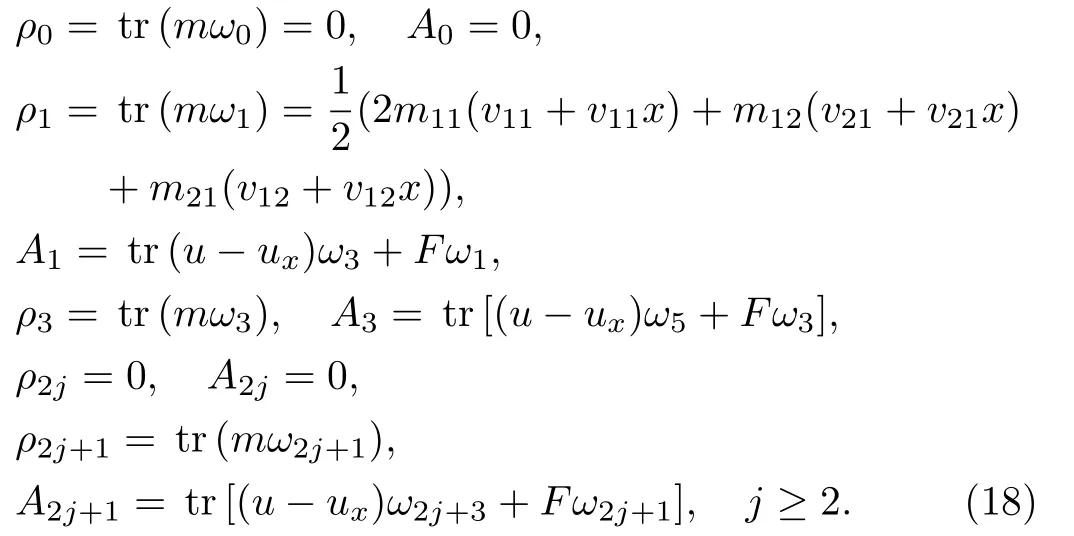
3 N-Peakon Solutions
As shown before,once having selected two undetermined matricesFandGsatisfying Eq.(4),we may obtain a matrix CH-type equation that possesses a zero-curvature representation and infinitely many conservation laws.The following technical lemma is useful for us to select such two matrices.
Lemma 1IfA,B ∈sl(2),thenAB+BAis a scalar matrix.
The lemma can be proved by a direct calculation.
Lemma 1 gives us a method to select functionsFandG.For example,we chooseFandGas follows:
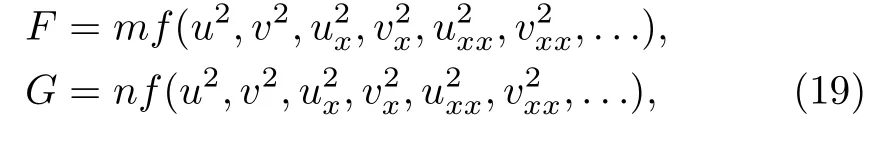
or

wherefis an arbitrary polynomial about the matricesu2,v2,u2x,v2x,...,uv+vu,uxvx+vxux,uvx+vxu,uxv+vux,or their linear combinations.Actually,from Lemma 1,we immediately conclude thatfis a scalar matrix,which in turn implies thatFandGsatisfy Eq.(4).Here we give the following two examples.
Example 1f=O(hereOdenotes zero matrix).In this case,F=G=O,then Eq.(2) is reduced to the following matrix CH-type equation:
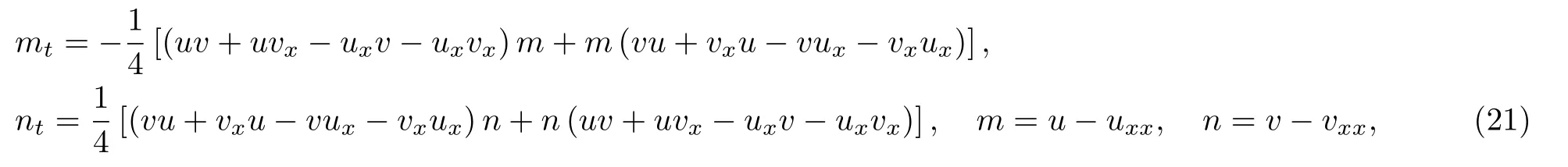
wherem,n,u,varesl(2) valued matrices defined by Eq.(3).
Example 2f=(1/4)(uv+vu −uxvx−vxux).In this case,
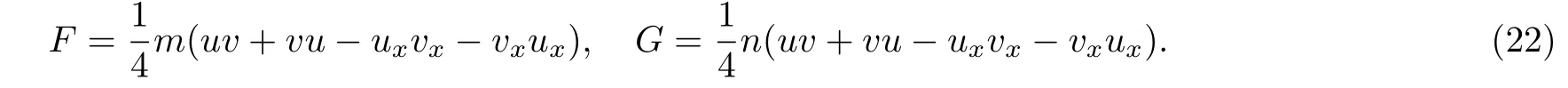
Then equation (2) becomes the following matrix equation:

wherem,n,u,vare defined by Eq.(3).
In the following,we show that Eq.(21) hasN-peakon solutions.To this end,we suppose theN-peakon solution of Eq.(21) in the following form
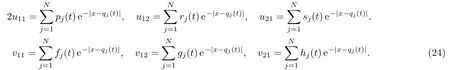
In the distribution sense,we have

where sgn(x) is the sign function.
Substituting these expressions into Eq.(21) and integrating against test functions with compact support,we arrive at theN-peakon dynamical system as follows:

Equationsqj,t=0 imply that the peakons are stationary and the solution is in the form of separation of variables.We now discuss the single peakon solution of Eq.(21).ForN=1,the aboveN-peakon dynamical system becomes
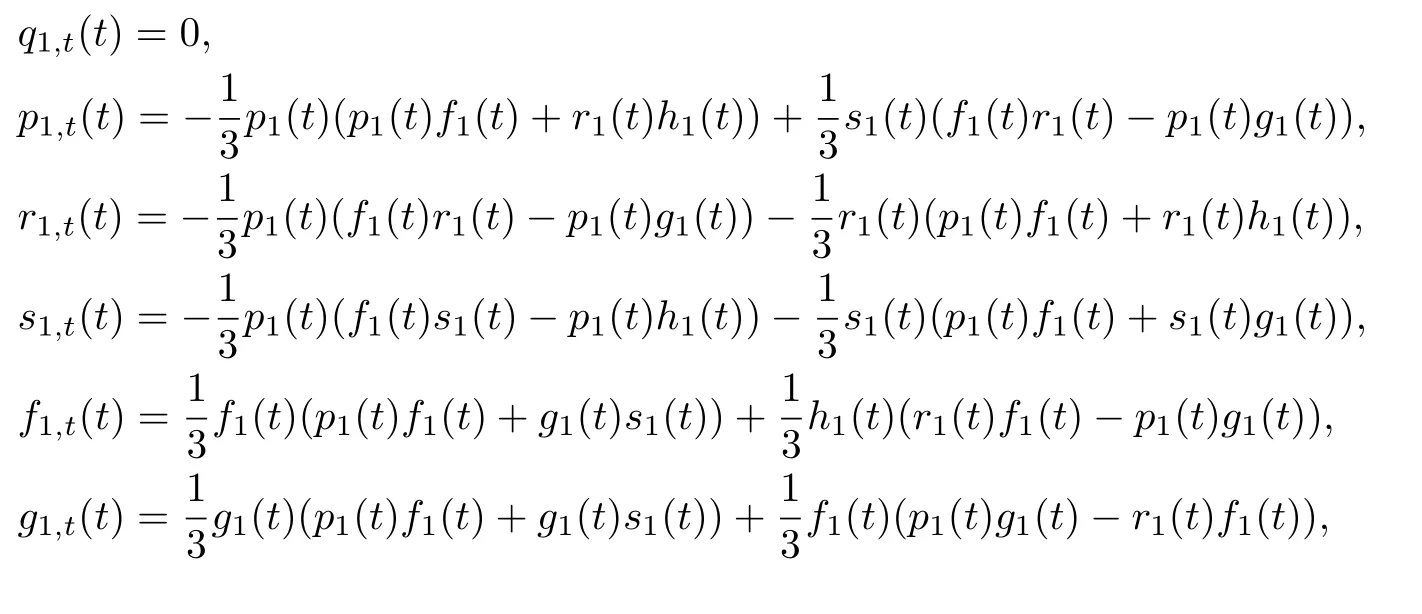

From Eq.(26),we can take
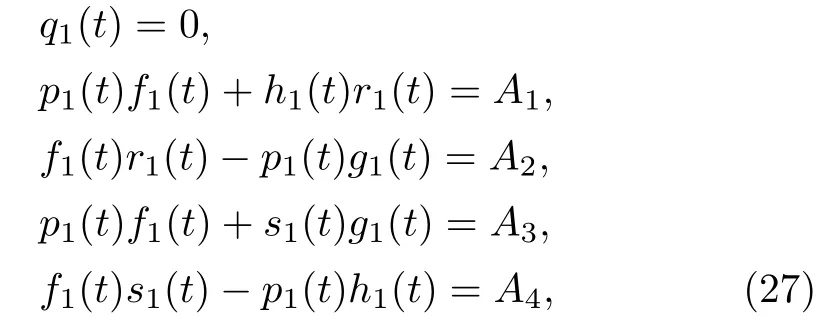
whereA1,A2,A3,A4are arbitrary constants.Let us specify the following cases:
Case 1(A1−A3)2−4A2A4>0.In this case,a solution of Eq.(26) is given by


whereCj,C′j,j=0,1,...,7,are arbitrary constants,and

Case 2(A1−A3)2−4A2A4= 0.In this case,a solution of Eq.(26) is given by
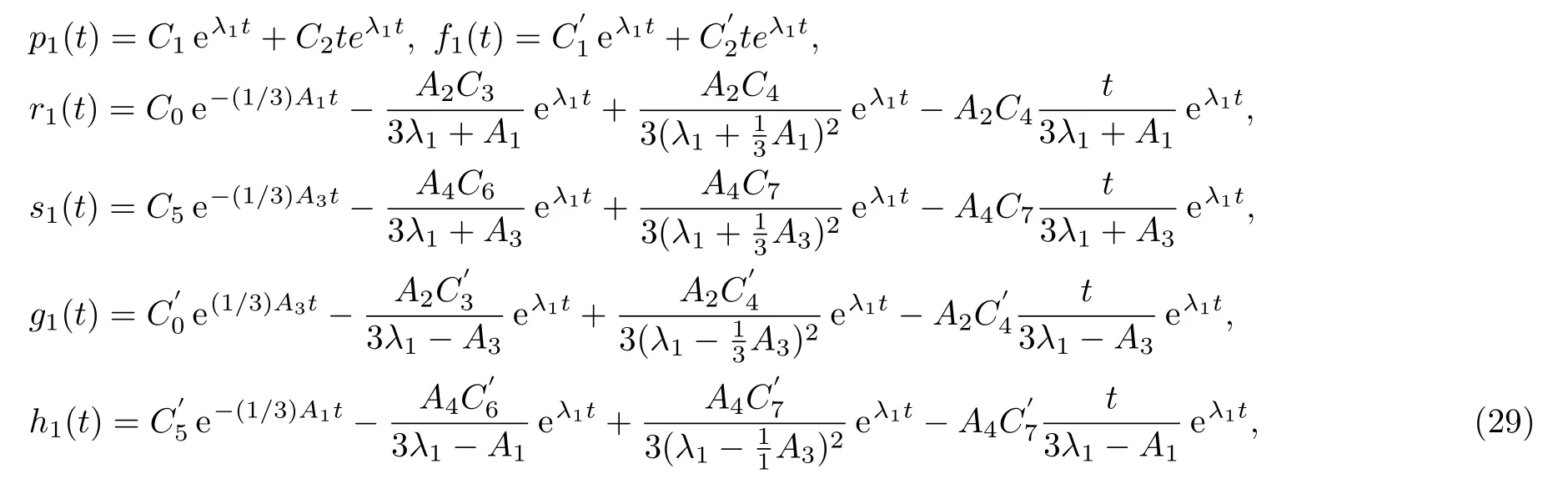
where
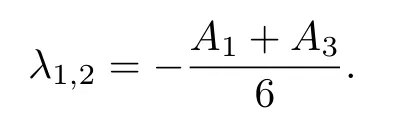
Case 3(A1−A3)2−4A2A4<0.In this case,a solution of Eq.(26) is given by
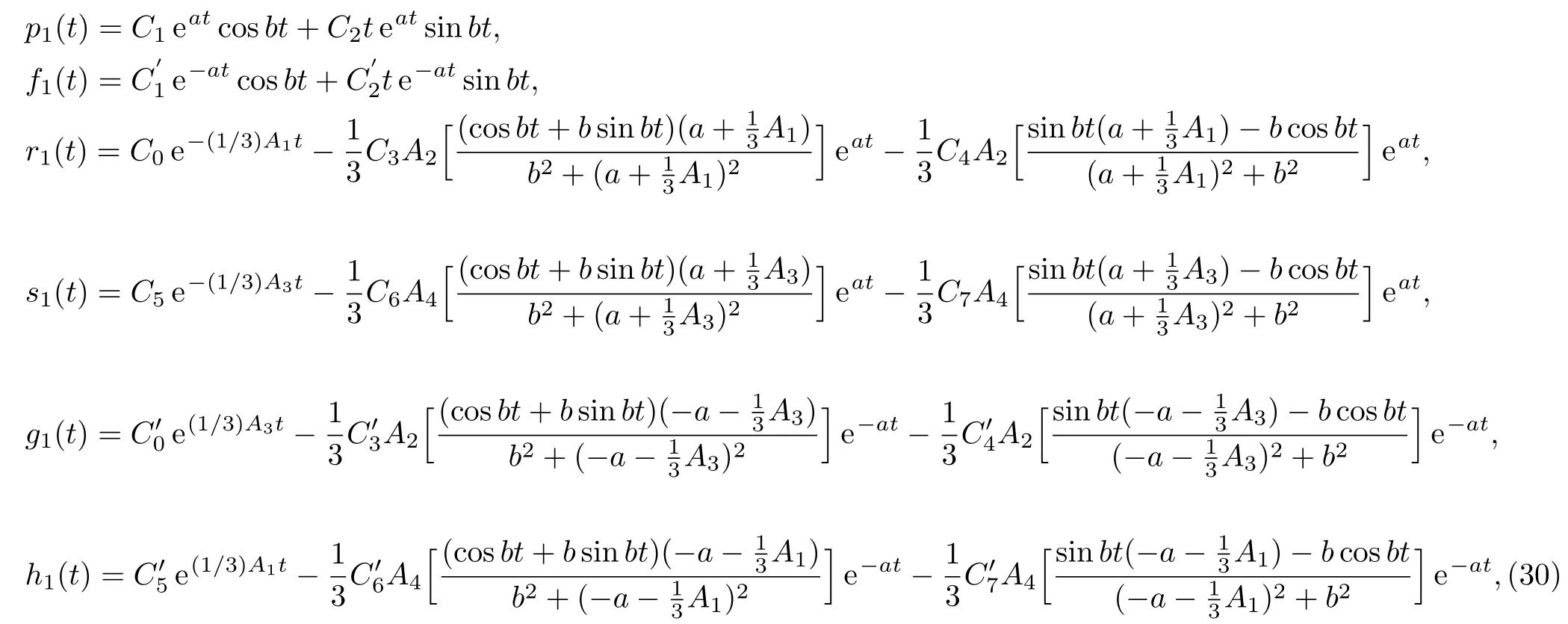
where
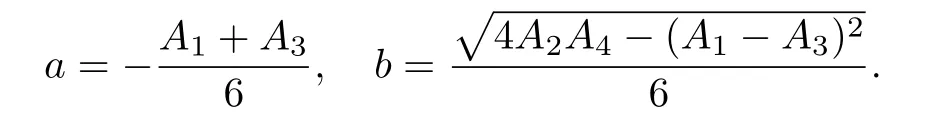
杂志排行
Communications in Theoretical Physics的其它文章
- Magnetohydrodynamic Stagnation Point Flow of a Maxwell Nanofluid with Variable Conductivity
- An Optimal Analysis for 3D Flow of Prandtl Nanofluid with Convectively Heated Surface
- The Effects of Wettability on Primary Vortex and Secondary Flow in Three-Dimensional Rotating Fluid∗
- An Improved Heterogeneous Mean-Field Theory for the Ising Model on Complex Networks∗
- Relativistic Self-Focusing of Hermite-cosh-Gaussian Laser Beam in Magnetoplasma with Exponential Plasma Density Ramp
- Periodic Orbits Around Kerr Sen Black Holes∗
