点云数据下的矿山巷道三维建模
2020-01-09石信肖王健王磊李志远付洪磊
石信肖,王健,王磊,李志远,付洪磊
(1.山东科技大学 测绘学院,山东 青岛 266590;2.兖州煤业股份有限公司兴隆庄煤矿,山东 济宁 272102)
0 引言
数字化矿山是实现矿山综合自动化开采的基石,而在矿山中,巷道是各种人工设施的重要载体,巷道贯穿于整个矿山体系,巷道数据以及巷道模型则是数字化矿山的重要组成部分。传统意义上矿山模型的构建主要有以下三种:第一种是借助巷道顶底板中心线数据与断面数据完成巷道重建建模;第二种是借助巷道中心线以及顶底板边界线完成巷道建模;第三种是利用巷道中心线以及边界线来提取高程的方法完成巷道重建[1]。这几种方法主要依靠断面特征点、导线点、巷道中线等数据进行建模,受到特征数据精度影响导致建模精度较低并且对巷道边界不能准确描述[2]。三维激光扫描技术可以快速获取物体表面三维数据集,所得点云数据精度高、密度大,具有较好的三维信息。因此借助点云数据可以构建更为精细的模型。精细建模一般在文物修复、城市建筑中应用较为广泛,对于巷道精细建模还有待完善。杜志强等[3]采用三维激光技术对巷道建模,研究了借助模型来绘制矿区纵横断面图以及大比例尺成图问题。江记洲等[4]采用圆柱面投影借助分冶算法进行三维巷道模型重建,这种方法仅局限于单站点云数据。赵小平等[5]将巷道实体抽象简化借助Arcsense平台采用组合法则进行三维模型构建。
三维激光技术虽然能快速获取大量巷道内部数据,借助点云数据所建立的巷道建模能够完整表达巷道信息,但对于所建模型的精度分析,以及面对大数据量点云模型的精细化重建,目前尚缺乏成熟的技术方案。现有的曲面建模软件如Geomagic[6]等面对狭长海量的巷道点云数据在构网时三角形边长较小,拟合的模型存在较多的孔洞。针对以上问题,本文基于加入约束条件的Delaunay生长算法,设置合适的边长阈值实现巷道点云整体精细构网,探讨了基于点云数据的矿山巷道建模的关键技术,并进行了实验验证和精度分析。
1 传统Delaunay 生长算法
传统的生长算法是指遍历离散点集中所有的点数据,找寻2个相距最近的2个点,两点连成线完成该点集数据的第一条初始边构建。随后依据Delaunay准则去判断并选取最合适的扩展点,初始三角形的构建到此完成,在寻找扩展点时主要的判断依据Delaunay外接圆准则[7]和夹角余弦值[8];随后对新获取的两边依旧根据Delaunay准则继续寻找合适的扩展点,完成三角形生长。反复遍历所有的点集完成此过程。
主要步骤如下:
步骤1:在集合N={Pi|i=0,1,2,…,n}中遍历N中所有的点,计算两点间的距离
(1)
距离计算需要进行n*(n-1)/2次;在计算距离的同时需要记录距离最近的两点并记为P1,P2,P1P2组成的边就是始边e1。

(2)

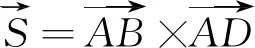
步骤 4:控制边长生长次数即曾经有过最优点的边长需要放弃,依此找寻余弦值最小的点作为最佳扩展点。
步骤 5:重复步骤3至步骤5,直到每个数据点都完成三角形构建。
由于生长算法在处理过程中需要不断遍历点集,前两步需要的时间为O(n),在步骤3、步骤4中,边长的引入耗用的时间更长可达到O(n2)。可以看出传统的生长算法用于二维平面,以外接圆的方式寻找三角化最优扩展点,计算量较大。
2 附加约束的Delaunay 生长算法
在三维空间中引入外接球来进行寻找三角网生长的最优点,借助外接球准则同时引入两三角网间的二面角、边引用、三角网内角和三角形大小等约束条件[9-12]。由此控制三角网的生长方向以及避免狭长三角形,使得拟合的曲面更加精细同时减少孔洞数量。本文为构建精细三角网模型,针对三角网边长选取不同的阈值来获取最佳模型。
2.1 约束条件
1)二面角夹角约束。三角网在生长时,借助初始三角网与待生成三角网之间的二面角来限制曲面的起伏变化。新三角网与原三角网之间的二面角角度越大表明两三角网之间的过度更加小,该连接处的曲面更加光滑。其中二面角夹角接近180°时两三角形处于同一平面。同时结合三角网的生长方向,新旧三角网的二面角以90°为临界值,当二面角小与90°时代表三角网向内生长,该点可能为错误点。因此对新旧三角网间的二面角给定一个阈值条件α,本文将阈值设为60°根据设定的阈值条件来控制三角网的生长方向,同时确保三角网拟合曲面的平滑性。
2)边的引用约束。在三维点集中,拟合形成空间三角网的拓扑关系更为复杂,点云数据量大拟合构网时三角面容易交叉形成重叠面片。对三角形边的引用次数加以约束,尽可能地减少单边多次重叠生长。空间三角网形成时,每个三角形初始引用次数均为1,为防止多个三角网引用同一边生长,以引用次数为2作为约束。当该边的引用次数为2次或2次以上则代表引用次数过多,放弃引用该边长,如果边长引用数为0或1,以此边进行三角形生长,引用次数加1并记录。
3)三角形的内角约束。按照 Delaunay 三角剖分的外接圆准则,等边三角形是生长最优的状态。但是实际处理过程中由于点云或其他问题容易导致狭长三角形的出现,这样导致后续曲面拟合时出现孔洞问题。以三角形内角大小进行约束,即设置当三角形内角为60°时为最优内角,控制最小内角度数设定阈值为15°,在尽可能保证三角形的形态下避免狭长三角形的出现。
4)三角形大小约束。三角形边长的大小对模型细节的体现有着重要影响。当扩大生长的三角形边长虽能节省构网时间但容易造成细节丢失,如果以过小的三角形进行生长,虽能保留细节但耗时以及孔洞问题会出现。因此借助设置边长阈值e来确定待生长的三角形大小。同时结合巷道狭长、点云数据量多的特点,适当扩大三角形边长兼顾模型细节优化构网时间。本文将边长阈值设为6 cm时,拟合的模型既能保留细节,同时耗时和孔洞较少。
2.2 评价函数
为了保证生长三角形能够正确合理的生长,设置多个约束条件,设置角的约束是为了保证三角形生长方向及正三角形的生成,设置边的引用约束主要是控制三角形的单一性和避免狭长三角形的出现。根据以上约束条件能正确快速地将点云三角化,但在实际三角化时,最优点的的选取往往难以同时满足边角附加的约束。引入函数f(PiPjPk)以此平衡各约束准则的权重,其中f(PiPjPk)的值越小代表获取的三角形最优。

(3)

2.3 算法流程
Delaunay 生长算法主要是最优生长点的选取,引入边角约束条件后,选取合适的三角形边长阈值条件,完成巷道点云曲面拟合。本文算法步骤如下:
步骤1:输入点云初始化,选取一点作为初始点记为P1,历点集找到与P1点最近的P2点,两点生成初始边P1P2;
步骤2:由P1P2依据三角形内角约束寻找P3点,根据余弦定理计算cos∠P1P2P3的值,检验是否通过设定的内角阈值,不通过重新寻找生长点。通过后根据设定的边长阈值条件,判断三角形边长e是否通过检验,以此获取最优生长点;
步骤3:获取初始三角形后,采用二面角对待生长的三角网进行生长方向进行控制,并重复步骤2,获取新的三角形。同时在后续三角形生成时需判断基线边的引用次数,即任何一条边最多只能是2个三角形的公共边;
步骤4:使用评价函数,平衡边角阈值条件的权重避免后续构网时局部最优。
遍历点集重复步骤2、3、4完成所有点集的三角构网。
3 实验与分析
3.1 测区概况
测区位于地下300 m处,环境复杂,地下场景较多,测区内潮湿闷热,道路泥泞,光线较暗,总测区面积较大,有可使用的已知控制点数个,测区内高程差7.5 m左右。测区分成两类:一类是采煤机掘进工作面,面积大约1 500 m2;另一类是运煤轨道,长度约为3 km,巷道环境如图1所示。

图1 巷道内部
3.2 数据采集和预处理
井下环境特殊而且有较多的人工设施,采用合理的数据采集方式对以后的数据预处理和建模工作有着重要影响,因此结合巷道区域特点,采用固定站式扫描和移动式扫描仪共同作业的方法,在煤矿工作面区域使用固定站式激光扫描仪,采用“步进式”扫描方法[13],即按照巷道走向进行扫描,同时借助仪器配套的靶球完成前后站数据的配准;巷道其余区域则采用移动式扫描仪进行数据采集。其中结合给定控制点坐标固定站式扫描仪共设站14站,移动式扫描仪由专业人员沿巷道行走一圈,完成巷道的整体数据采集,获取所需要的全部巷道信息。
通过给定的实际控制点坐标结合数据形式选择如下配准方式:在点云处理软件下对工作面部分的点云以基于靶标的方式进行点云配准。移动式扫描仪导出的数据经配套的软件处理后,与工作面点云以基于特征的方式进行配准,从而得到巷道整体点云数据。最后借助给定的控制点坐标将所有的点云数据统一到井下坐标系统中。再对配准后的点云数据进行滤波和去噪,得到预处理完成后的巷道点云,如图2所示。

图2 巷道点云
3.3 巷道三维建模
精细建模是数据处理的重要阶段,精细的模型能够更好地反应点云信息。将预处理好的点云数据采用构建三角网的方式建立初始巷道模型,随后对模型进行后处理,从而得到最终巷道模型。
1)三角网阶段。为证明本文方法的可行性选取巷道中2组点云数据进行拟合。第一组为巷道拐角位置,第二组为巷道平巷位置。其中第一组数据点云长度为22 m,点云个数为12 917个,第二组点云长度为45.74 m,点云个数为27 378个。2组点云分别用不同边长约束条件下的Delaunay生长算法和Geomagic软件分别拟合,结果如图3和图4所示。

图3 第一组点云数据及拟合结果

图4 第二组点云数据及拟合结果
本文选取巷道中2组代表性的数据为例,具体数据结果见表1和表2,通过设置不同标准差倍数的三角网边长阈值对点云构网。对比发现第一组点云数据为巷道拐角处,此处点云曲率变化较大,同时交叉位置曲面点云较为复杂。当边长阈值过小即e=3 cm时,虽然对物体表面细节展现较好,但耗时长,同时在拐角细节处出现了构网孔洞,软件在拟合时出现了同样问题。扩大边长阈值设为6 cm时,既能保留细节特征同时拟合的孔洞也最少。最后增大边长阈值为9 cm时,孔洞会减少,拟合时间也可以缩短,但由于边长过大导致细节特征丢失。第二组点云数据为平巷处,此处点云特征较为简单,本文算法与软件算法结果都较好,在保留细节特征的前提下边长阈值设为6 cm用时较少。最终在考虑细节特征,孔洞数目
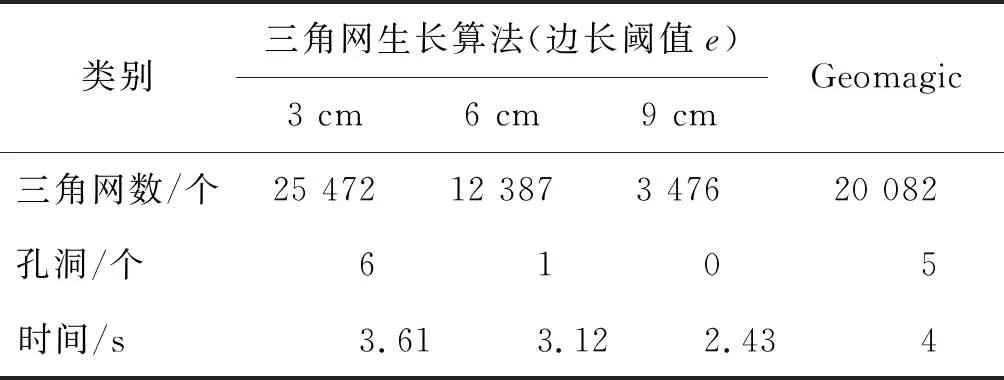
表1 第一组点云数据结果
以及耗时情况,选用边长阈值6 cm对巷道点云整体构网拟合,巷道整体三角网拟合结果如图5所示。

表2 第二组点云数据结果

图5 巷道三角构网效果
2)模型后处理。在实际处理构网过程中由于点云噪声等原因,拟合的曲面总会存在孔洞。将利用本文算法拟合好的巷道模型在Geomagic中进行后处理[14-16]。首先是整理孔洞处三角网以曲率进行空洞修补,然后采用网格医生对修补处模型进行网格细分处理,最后对模型进行调整和打磨使模型更加光顺,具体效果如图6所示。

图6 处理后巷道模型效果
3.4 模型分析
建模精度是评判模型质量的重要指标,本文将构建好的巷道曲面模型与原始点云数据进行对比分析,从三维整体和二维剖面2种方式对模型进行精度分析评定[17]。
1)三维整体对比分析。将点云数据与巷道模型对齐后,点云设为参照,与构建的精细模型进行三维整体对比,对比后的结果以三维色谱图的形式进行展示,结果如图7所示。

图7 巷道模型3D色谱图
其中整体偏差结果如表3所示。

表3 整体对比偏差结果 cm
2)二维剖面对比分析。经整体对比分析发现工作面部分偏差较大,选取工作面部分进行二维剖面分析。对工作面部分分别进行xz、xy2个方向的剖切,从多个方向对模型进行二维剖面的对比分析,各剖面结果如图8所示。
可以看出整体误差较小,模型在整体3D误差分析时标准偏差在5 cm以内。模型误差主要在于工作面部分。其原因是由于扫描时工作面部分存在较多人工设施,数据采集时存在遮挡问题导致巷道点云数据缺失,点云拟合时存在孔洞,后期空洞的修补导致模型产生一定误差。同时以剖切面的方式进行点云与截面曲线进行对比,其标准差稍大在10 cm以内。与Geomagic软件对比,使用该方法建立的巷道模型孔洞较少,降低了孔洞修补造成的误差,精度较高,总体达到了井下巷道精细建模的要求。

图8 巷道模型工作面位置剖面图
剖面分析主要是点云数据与截面曲线进行对比。其中偏差结果如表4所示。

表4 局部对比偏差结果 cm
4 结束语
本文采用高精度的三维激光扫描仪完成了煤矿巷道的三维数据获取,实现了不同仪器数据下的点云配准拼接等预处理工作,借助带约束的Delaunay生长算法选取合适的三角网边长阈值,完成了巷道三维模型重建。同时以三维整体和二维剖面2种方式对巷道模型进行误差分析,对模型精度进行评判,得到符合精度要求的三维巷道模型,最终实现矿山巷道实景化,对提升煤矿信息化,井下可视化有重要意义,为智慧矿山建设奠定基础。
目前,巷道三维建模中仍存在急需解决的问题,如模型数据的组织与管理、提高模型修整的自动化、模型精度的评判指标等,是今后需要改进的方向。
