一种新的遥感影像色彩均衡方法

刘小帆，周国清，岳涛，陆妍玲

(桂林理工大学 广西空间信息与测绘重点实验室，广西 桂林 541006)

0 引言

遥感技术的发展为地物信息研究提供了一种非常直观的方法，如历年遥感影像为地物监测以及水域研究等提供了非常宝贵的历史资料。早期的光学遥感卫星包括了美国侦察卫星系统(CORONA、ARGON、LANYARD)[1]和逐步更新换代的Landsat卫星系统等[2]。这些卫星覆盖范围广，影像分辨率满足一般情况下的地物研究。当研究区域受限时，可以通过镶嵌目标影像来扩大研究区域。

由于光学影像的敏感性，影像镶嵌后可能产生明显的辐射差异。Yu等[3]在直方图均衡法的基础上归纳出全局最优法和局部最优法用于消除镶嵌后影像的亮度差异。全局优化法中，Stark等[4]提出了影像的适应性直方图规定化法，根据影像的特征来进行直方图规定化处理达到色彩均衡的目的；Jun等[5]提出自适应性小波变换用于处理影像重叠区域波段不一致的问题；Celik[6]等提出多维直方图均衡化方法，通过多维度直方图来使影像的直方图更加具有普遍性，实现色彩均衡。然而这些方法并不适用于灰度信息较为丰富的影像或是重叠区域较大的影像。针对上述方法的不足，Zhou等[1]在局部优化法的基础上提出辐射均衡法用于实现亮度均衡。该方法通过分析影像重叠区域的灰度信息并进行权重分配，实现影像平滑渐进。但是受按权分配模型的影响，该方法在影像处理区内会产生灰度阶分块现象，影响亮度一致性[7]，并且在重叠区域小的情况下无法取得较好的效果。

综上所述，如何使灰度影像实现不受限制的实现亮度均衡，是均衡工作的核心研究内容[8]。本文在传统的辐射均衡方法基础上，提出使用亮度因子模型对辐射差异进行消除。该方法避免了传统局部优化法受重叠区域大小的限制用于处理灰度信息丰富的影像，不会产生由固定权重分配模型导致的灰度阶分块现象。本文使用ARGON KH-5卫星影像[1]以及Landsat系列卫星影像进行亮度均衡处理验证，实验结果表明该方法明显优于传统的全局优化法和辐射均衡法。

1 传统辐射均衡方法

目前传统的辐射均衡方法已经广泛用于处理重叠区域较大影像的辐射差异，其主要从两方面对影像辐射差异进行消除：一方面统计重叠区域的灰度信息并建立线性参数模型，使目标影像具有相同的平均灰度级[3]；另一方面根据重叠区域内原始影像的亮度信息以及权重函数模型进行影像亮度均衡化处理[1]。权重函数模型能够改变重叠区域内各级灰度值所占权重，使较亮的部分具有较小的权重、较暗的部分具有较高的权重[1]。

传统的辐射均衡法使用权重函数来进行辐射差异的消除[1]，可按如下方法表示为：

image3=p*image1+(1-p)*image2

(1)

式中：image3代表镶嵌后的影像；image1、image2代表目标影像；p代表权重函数式，且p∈[0，1]。根据目标影像辐射区域的图幅宽度结合权重函数式可以进一步得到权重模型：

(2)

式中：m和n代表目标影像辐射区域的长和宽，[p1，p2，…pn-1，pn]代表权重函数在影像每一列所占的权重。

2 亮度因子辐射均衡法

2.1 亮度因子模型的建立

亮度因子模型首先要实现影像的羽化渐进，其次要消除由斜率变化产生的灰度阶阶分块现象，因此本文使用圆的弧线公式推算亮度因子函数式。与传统方法将作用区间归一化为[0，1]不同，本文将灰度影像处理区域拉伸到[0，2]并建立独立坐标系，以图形的左节点为原点，以1为半径，(0，1)和(2，1)为圆心分别作圆：

(3)

(x2-2)2+(y2-1)2=1

(4)

式中：x1∈(-1，1)，x2∈(1，3)，y1∈(0，2)。根据提取到的弧段可进一步表示为：

(5)

将p=y1，k=y2,则组成的亮度因子为：

(6)

通过上式计算目标影像的图幅宽度，生成相应宽度的亮度因子。其中羽化度随函数斜率的增加而增大，羽化度越高，灰度变化越剧烈；羽化度越低，灰度变化越平滑。根据灰度影像的大小可以进一步得到如下亮度因子组成的渐进函数矩阵：

(7)

式中：m和n代表了影像的长和宽。矩阵中的每一个元素代表相应的亮度因子系数。根据辐射均衡算法的关系式得基于亮度因子辐射均衡方法得到的平衡影像(B_img)为：

(8)

设镶嵌线(M)、目标影像1(t_img1)、目标影像2(t_img2)的表示如下：

(9)

式中：x代表目标影像1的矩阵；y代表目标影像2的矩阵。

2.2 灰度偏差的消除

由于亮度因子辐射均衡法以像素为单位，镶嵌线本身也是由多个像素点组成，所以通过亮度因子以镶嵌线为中心对辐射差异进行处理会产生一定范围的灰度偏差(图1)。

图1 灰度偏差示例

灰度偏差集合可以通过如下公式表示：

Δg={Δg|f(x)-g(x)}

(10)

式中：f(x)、g(x)代表色彩均衡处理后的2幅目标影像间存在的差值。提取地物信息可知这种差值的分布满足高斯分布的特征，即离对接口越近的位置灰度偏差越大，离对接处越远的位置产生的灰度差值越小[9]。解决该问题需要选定灰度偏差区域并设置高斯滤波窗口对产生的灰度偏差进行消除。设定处理区域长度为t，设高斯滤波处理后的区域灰度值为g(x)，设选定区域外的灰度值为h(x)，那么它们的差值为：

g′(x)=g(x)-h(x)

(11)

在处理区内，根据实际情况，通过幂函数方程y=x将灰度差值分布在各缓冲点上，使影像与高斯滤波处理值之间产生平滑的过渡，则有：

(12)

即得到缓冲点的灰度值。将缓冲区域和高斯滤波器组合便得到平滑型一维高斯滤波校正模型：

(13)

式中：在影像坐标系下x∈(0，m)，m代表图幅宽度；δ表示标准差；μ表示均值。该方法有效地消除影像对接处的灰度偏差，同时能够达到平滑灰度值的目的。

3 实验与分析

3.1 实验数据集

为验证亮度因子辐射均衡方法的有效性，本文使用2种卫星在不同条件下镶嵌的影像数据进行实验。第一幅影像数据是由周国清教授提供的来自Declassified Intelligence Photography Project中格陵兰岛部分数据，如图2所示。第二幅影像来自Landsat-5卫星和Landsat-7卫星分别于2011年10月和2003年5月搭载了专题制图仪(TM)以及增强型专题制图仪(ETM+)2种不同传感器在中国黑龙江地区拍摄的遥感影像，2幅影像的中心纬度分别为46.029 8°N和47.433 7°N，127.931 04°E和128.375 1°E(飞行高度705 km，分辨率30 m，波段分别为7、8，扫幅宽度为185 km、170 km)。并使用ENVI5.1软件进行镶嵌，镶嵌后影像如图3所示。

图2 1963年DISP项目中格陵兰岛镶嵌后的部分遥感影像[1]

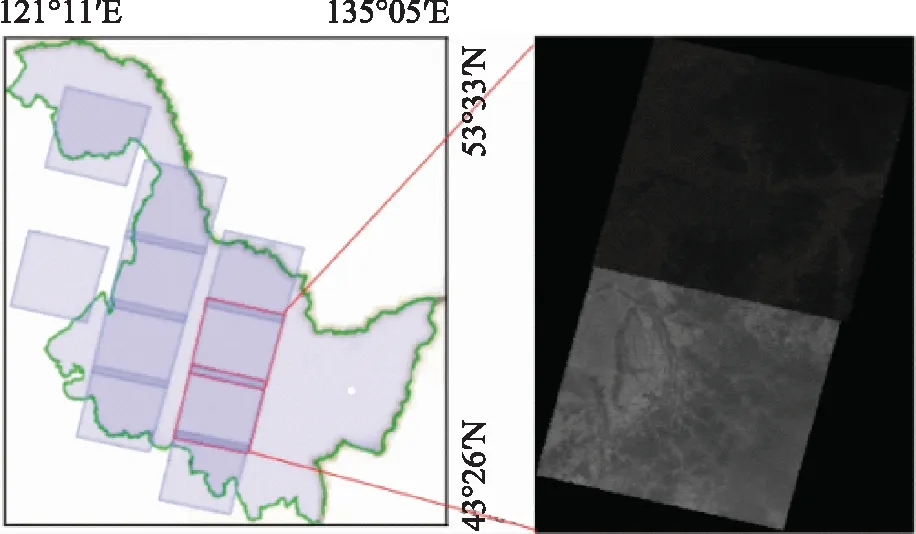
图3 Landsat系列卫星在黑龙江地区的拍摄航带

3.2 实验步骤

亮度因子辐射均衡方法具体实施流程如图4所示。该方法主要从3个方面对影像进行处理。首先对镶嵌后的目标影像进行信息统计，包括灰度值均值与标准差2项指标[10]；然后根据统计所得灰度信息对影像灰度模式进行识别并建立相应的亮度因子模型；最后通过平滑型高斯滤波对灰度偏差带进行消除，实现辐射差异的消除。

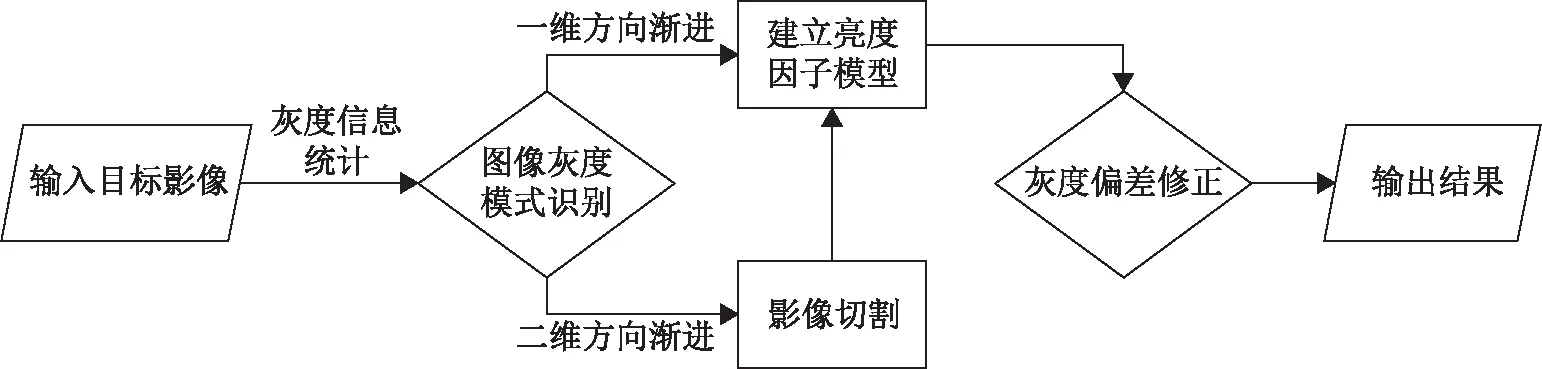
图4 基于亮度因子的辐射均衡方法实现流程

3.3 实验与结果

1)ARGON KH-5卫星影像实验与结果。通过亮度因子辐射均衡方法对格陵兰岛影像进行处理并与传统的辐射均衡方法做出对比，原始影像如图2(b)所示。由于目标影像未知，所以本次实验采用局部取样法进行灰度信息统计并将影像按照无用区域(如图5中白色注明的Ⅰ区域)和灰度变化区域(图5中蓝色和红色注明的区域)划分。

图5 目标影像灰度特征的局部取样

便于统计，以镶嵌线为界，将右上方的影像命名为目标影像1，将左下方的影像命名为目标影像2。根据提取出的目标影像局部特征区域进行灰度信息统计。具体信息如表1、表2所示。

表1 目标影像1各特征区域灰度信息统计

表2 目标影像2各特征区域灰度信息统计

由特征区域灰度信息可知，目标影像1的灰度呈现出递进的特征，而目标影像2跟区域间则具有较大的亮度差异，因此要实现二维方向上的渐进。根据这些灰度信息，通过公式(9)以影像镶嵌线和区域分界线为基准建立亮度因子模型。将该模型作用于影像上，其结果如图6(a)所示。处理后的影像由于亮度因子拼接处产生的灰度偏差导致镶嵌线处形成了线性带拼接缝[11]。根据公式(11)使用二维方向的平滑型高斯滤波校正灰度偏差，实验结果如图6(b)所示。

图6 亮度因子辐射均衡方法的处理与灰度校正

将本文方法(图7(c))与原始影像(图7(a))、Zhou等[1]提出的辐射均衡方法(图7(b))，以及本文提出的亮度因子辐射均衡法进行比较，结果表明本文提出的亮度因子辐射均衡方法有效消除了镶嵌线，实现色彩均衡。

图7 原始影像与2种方法处理影像后对比

2)Landsat系列卫星影像的实验。Landsat卫星拍摄的影像如图3所示。由于传感器不同的原因，导致这组镶嵌后的影像具有较大的灰度差异。本文使用亮度因子辐射均衡方法对影像进行处理并与全局最优法做出比较。首先通过亮度因子辐射均衡方法对该影像进行均衡化处理。在目标影像已知的情况下对目标影像的特征区域进行灰度信息统计。镶嵌后区域示意图如图8(a)所示，其中红色内容代表目标影像1，蓝色内容代表目标影像2，白色内容代表镶嵌线位置。目标影像的灰度统计如表3、表4所示。

图8 使用亮度因子辐射均衡方法处理影像结果

表3 目标影像1的灰度信息统计

表4 目标影像2的灰度信息统计

由表3、表4可知目标影像内不存在明显的差异，因此只需对镶嵌后的影像进行一维方向上的渐进处理。接下来以镶嵌线为基准生成亮度因子模型，并将亮度因子直接作用到整幅遥感影像并使用平滑型高斯滤波校正影像接口处的灰度偏差。最终得到实验结果如图8(b)所示。

原始影像的灰度直方图如图9(a)所示，使用本文提出的亮度因子辐射均衡方法处理后的影像灰度直方图如图9(b)所示。

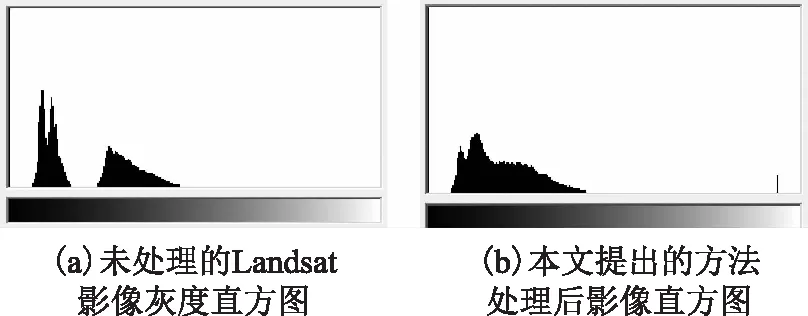
图9 2种方法的影像直方图对比

使用全局最优法对影像进行处理。该影像重叠区域较小，因此理论上使用全局最优法能够达到极好的效果。该方法通过分析目标影像影像重叠区域的灰度信息并建立线性参数模型使镶嵌后的目标影像的灰度值频率得以趋近。其结果如图10(a)所示。结果表明，该方法造成大面积的灰度信息失真，如图中红框内的影像信息。相比较来讲，使用基于亮度因子的辐射均衡方法很好地实现了灰度数据的融合(图10(b))。

图10 2种方法处理影像后结果对比

3.4 实验分析

本文选择了2幅不同原因导致的亮度差异影像进行实验，并对比标准差与灰度直方图2项指标进行分析。首先，本文采用标准差来衡量均衡化质量。标准差能够反映出灰度平均值的离散情况；同时，标准差越小代表影像反差越小，其统计结果如表5所示。

表5 实验影像标准差统计

第一组实验中原始影像由于亮度差异较大因此灰度信息较为丰富，它的标准差为0.152 0；通过辐射均衡方法处理后影像的方差降为0.150 3，相对来说有效实现了色彩均衡；而基于亮度因子的辐射均衡方法在处理影像后使影像的方差降至0.110 9，非常有效地消除了亮度差异。同样，第二组实验中原始影像的方差达到0.133 4；经过全局优化法后产生了明显的噪声并使其方差达到0.163 4；使用本文提出的方法则使方差降到0.126 1，表明该方法有效实现影像的均衡化。

在对照组实验中：第一组实验中亮度因子辐射均衡方法对比辐射均衡法有效地消除了影像的镶嵌线并且未产生灰度阶分块现象，视觉上实现“无痕连接”。第二组实验中本文提出的方法相比全局优化法很好地实现不同传感器下的灰度数据融合。

4 结束语

本文针对传统的全局优化法以及局部优化法法的缺点提出了基于亮度因子的辐射均衡方法。该方法能够满足影像的自特殊性并具有普适性，可以实现灰度数据融合。如何使亮度因子在拼接处有效减少灰度偏差是未来主要的研究方向。

致谢：本文的最终完成感谢广西八桂学者团队。