用轴切法测量圆锥螺纹塞规基面中径

董良海 邵丹 / 无锡市计量测试院

0 引言

圆锥螺纹塞规主要用于综合检验密封管工件内螺纹。其中常见的有英制密封管螺纹量规（55°）和美制密封管螺纹量规（60°）。基准平面上的中径是圆锥螺纹塞规的主要参数，目前常用的测量方法有测球法和螺纹扫描法，但是这两种方法对于设备的要求比较高，不太适用于一般企业。本文提出了一种利用万能工具显微镜轴切法测量基面中径的方法，经实际验证，效果良好。

1 测量方法

测量前，一般需先将塞规手柄卸除。检查塞规顶尖孔是否完好，如有毛刺则要用高粒度油石打磨光滑，并用溶剂汽油清洗干净。

将被测塞规安装在工具显微镜的顶尖架上，根据被测螺纹的螺距选择并安装好合适的测量刀，螺距为0.5～3 mm，选用刃口与分度线间距为0.3 mm的测量刀；螺距为3～6 mm，选用刃口与分度线间距为0.9 mm的测量刀，所选用的测量刀事先应进行校准，其刃口与分度线间距误差一般不大于±0.5 μm。调整焦距进行对刀，使测量刀刃在螺纹轴线平面上与螺纹牙型轮廓密合，并刀刃口影像清晰。对刀前，应根据被测螺纹的螺旋升角使显微镜的立柱倾斜一个角度，在正式测量时，显微镜的立柱应恢复零位。

测量应在被测螺纹的前、后端进行，如图1所示。选定第一个测量位置后，瞄准测量刀分度线，使测量刀分度线与目镜中相应虚线对准，读取和记录万能工具显微镜纵横向坐标示值（x1，y1)，保持纵向位置不动，横向移动显微镜到螺纹轴线的另一边，瞄准测量刀分度线，读取和记录第二个坐标值（x1，y2)，两次横向测量示值之差即为x1位置处的中径测量示值。为消除螺纹轴线与纵向坐标轴线不平行引起的系统误差，应在螺纹牙型左、右两侧各测量一次，再得到x2位置处的中径测量示值。由于圆锥螺纹塞规存在中径锥度，因此两次测量计算的平均值作为（x2+x1）/2 位置处的中径d2a：

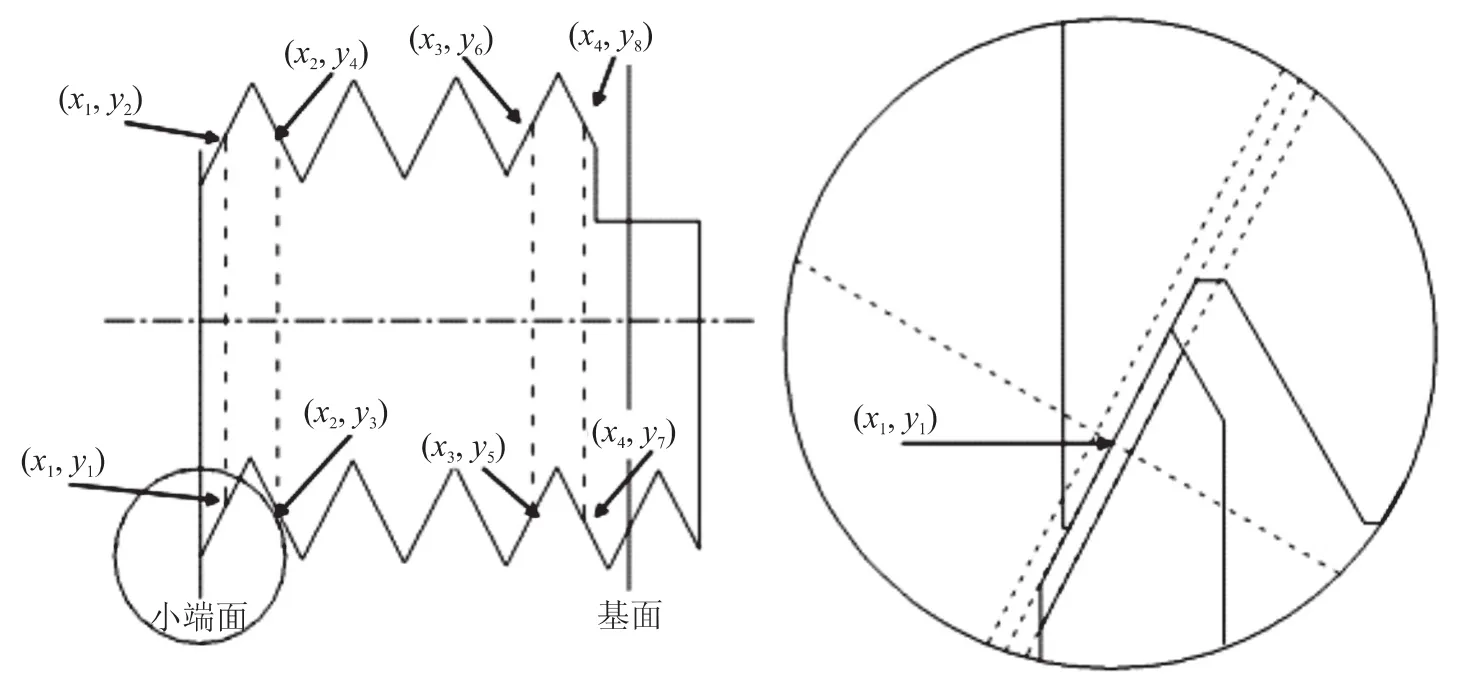
图1 轴切法测量中径示意图

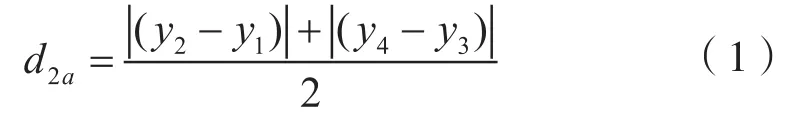
按同样步骤，在被测螺纹的后端进行测量，测量位置应尽可能靠近基面，得到(x4+x3)/2位置处的中径d2b：

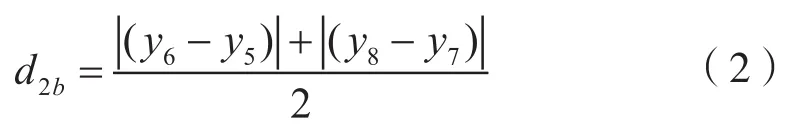
根据基准平面位置xl1计算基面处中径d2：

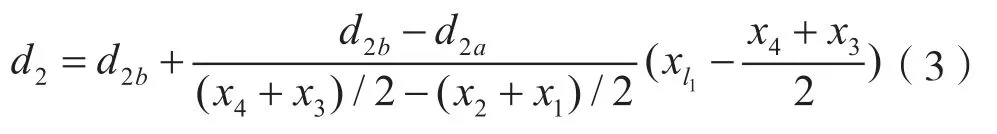
式中：d2——圆锥螺纹塞规基面中径，mm；

d2a——塞规前端（靠近小端面）中径，mm；

d2b——塞规后端（靠近基面）中径，mm

2 测量结果的不确定度评定

2.1 测量模型

将式（3）简化为

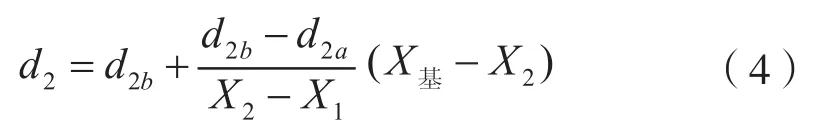
式中：X1——塞规前端中径距小端距离，mm；

X2——塞规后端中径距小端距离，mm；

X基——塞规基面距小端距离，为常数，mm

2.2 灵敏系数

对（4）式中各影响量求偏导数，得：

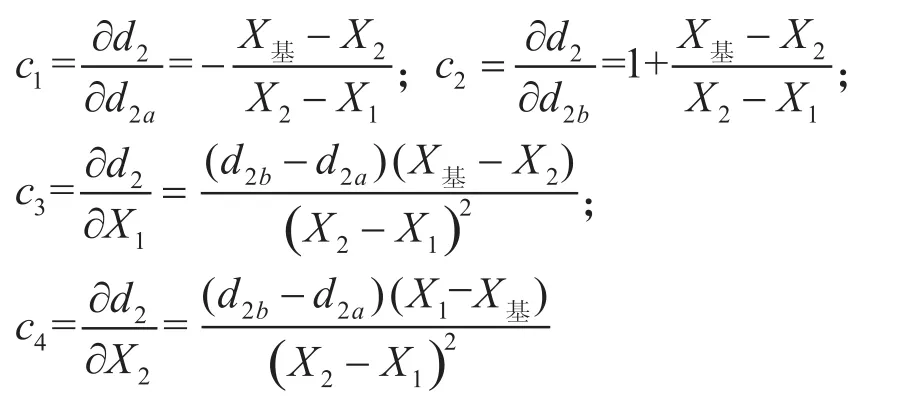
式中：c1，c2，c3，c4分别为前端中径测量值，后端中径测量值，前端中径测量位置，后端中径测量位置对基面中径影响量的灵敏系数

实际测量时，根据实际测量位置，可计算得到各测量值对中径的影响量。

以R3/4塞规为例，实际测量时，根据R3/4塞规的实际牙数确定测量位置，假定前端中径测量位置为距小端面0.5P的位置，后端中径在距基面-0.5P（P= 1.814 mm）的位置处测量(该塞规只有一个台阶面，因此测量时可以通过旋转量规尽量避开台阶面找到靠近基面处的全牙型进行测量)。经过计算可以得到：

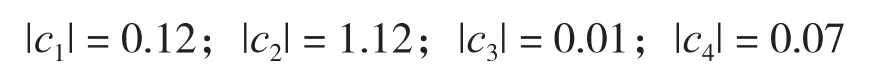
通过计算灵敏系数可以发现，基面中径测量的主要不确定度来源为前后截面的中径测量误差，后测量面的位置测量误差，由前测量面的位置引入的标准不确定度可忽略。

令u(d2a) =u(d2b)，则

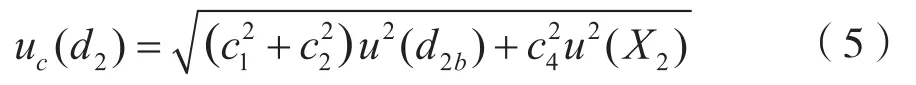
式（5）中，u(d2b)可认为是用轴切法测量圆锥螺纹塞规任一截面中径时引入的标准不确定度，主要由u1，u2，u3，u4四个分量构成，由后测量位置引入的标准不确定度为u(X2)。

2.3 标准不确定度评定

2.3.1 由万能工具显微镜示值误差引入的标准不确定度分量u1

在万能工具显微镜上用轴切法测量锥螺纹中径时，取牙型左右两侧中径值的平均值做为中间位置处的中径值，万能工具显微镜的最大允许误差为MPEV：（1 +L/100）μm，按均匀分布计算：

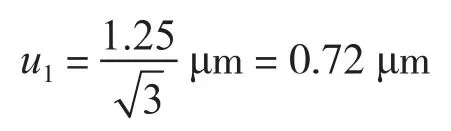
2.3.2 由测量刀分度线与刃口距离误差引入的标准不确定度分量u2

应选择未磨损的测量刀进行测量，测量刀的分度线与刃口间的距离误差为±0.5 μm，每一个截面需要用两把测量刀，按均匀分布计算，考虑到螺纹牙侧角的影响，测量刀分度线至刃口距离的误差对螺纹中径的影响应乘以系数则

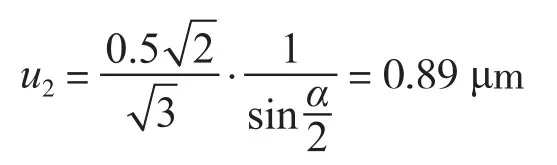
2.3.3 由测量重复性引入的标准不确定度分量

在重复性条件下，连续测量某一截面中径10次，计算其实验标准偏差：

即：u3=s=0.8 μm

重复性测量时已经包含了对刀误差、对线误差及分辨力误差，因此在评定时不予考虑该三项误差带来的标准不确定度分量。

2.3.4 由被测螺纹及相关测量程序等未明确因素引入的标准不确定度u4

在用轴切法测量过程中，被测量规的形状误差，测量刀的密合度以及测量程序中未明确因素等都可能对测量结果造成影响，其约为

u4= 0.5 μm

由此可计算得到用轴切法测量圆锥螺纹塞规任意截面中径产生的合成标准不确定度为

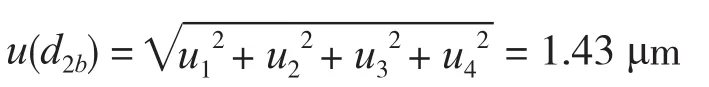
2.3.5 由后测量位置引入的标准不确定度u(X2)

u(X2)的分量组成与u(d2b)类似，其中测量刀分度线至刃口距离的误差对轴向距离的影响系数变为通过实际计算后得到：

u(X2) = 1.0 μm

2.4 扩展不确定度

由式（5）可以基面中径的合成标准不确定度为

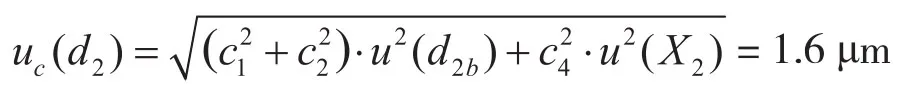
取包含因子k= 2，则扩展不确定度U= 3.2 μm。

3 测量误差分析

实际测量时，根据塞规规格不同以及台阶面形式的不同，测量时距离基面的位置可能也会不同。表1列出了后端测量位置距基面不同位置处时的灵敏系数变化。

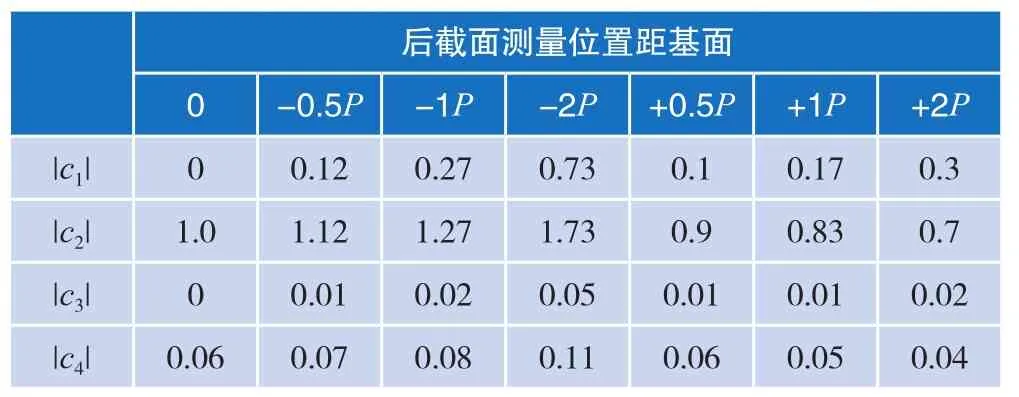
表1 后端测量位置距基面不同位置处时的灵敏系数

通过表1可以发现，当后截面测量位置在基面上时，该位置处的中径测量误差即为基面中径测量误差。当测量位置小于基面时，随着距离的增加测量误差有一个明显的放大作用。当测量位置大于基面时，影响塞规基面中径测量准确度的主要因素为前后端两位置的中径测量误差，无明显放大。因此测量时，测量位置应尽可能地靠近基面。

除仪器本身的准确度外，用轴切法测量塞规基面中径的另一个主要误差来源为测量者的熟练程度，包括对刀误差、对线误差、示值误差等，需要操作者加强测量熟练度。

4 结语

通过实际测量与不确定度分析，可以看出用万能工具显微镜轴切法可以准确测量圆锥螺纹塞规的基面中径。对于一些小型螺纹加工或使用企业来说，不可能配置昂贵的螺纹测量专用设备，因此通过轴切法测量圆锥螺纹塞规的方法可以有效地帮助企业解决难题，使其提高产品质量。