基于正负序分离的锁相环

2020-01-09李静静赵健上海市计量测试技术研究院

上海计量测试 2019年6期

李静静赵健 / 上海市计量测试技术研究院

0 引言

随着分布式发电系统的广泛应用，大功率发电设备为社会提供的能量是可观的，因此，大功率发电设备的可靠性也是非常重要的。电网扰动器作为考核大功率分布式发电设备检测系统，将会由小功率转变到大功率。现在大功率电网扰动器大多采用并联方式来扩展自己的容量。而对各个并联单元要确保与电网的同步性，必须能够快速、准确地实现对电网基波相位、频率等信号的锁定跟踪。

锁相环可以获取电网电压的相位角，它的基本作用是获取三相电网电压正序分量的相位信号，必要时还可以提供频率、幅值信号，锁定的这些信号都会参与电力变换装置的控制过程。正因如此，锁相环的性能好坏直接影响整个电力变换装置的输出效果的优劣。

SPLL中最常用的是单步坐标系的软件锁相环（SSRF SPLL），对于三相平衡电压条件下的电网电压有比较好的锁定效果[1]。但是当电网扰动器模拟电网三相不平衡电压故障时，此时该种锁相环带宽很低，降低了系统的动态性能，在实际工程应用中不合适。文献[2]采用延时的方法去除电网电压的直流偏移量和负序分量的作用，但是延时时间是定值，当电网频率不恒定时，这种锁相效果会大打折扣。

针对大功率电网扰动器各个并联单元的同步性问题，本文研究基于双同步坐标变换的锁相环方法。当三相电压不平衡时，能够快速地使三相电压的正序和负序分离，这样正序负序的幅值、频率和相位就能分开来进行分析，通过仿真验证了该种方法的正确性。

1 SSRF SPLL在三相电压不平衡条件下的分析

图1为此锁相环的系统框图。工作原理为：把三相电压分解到旋转dq轴坐标系中，Uq的正负反映了d轴与电压U的相位关系，Uq＞ 0，则d轴滞后U；Uq＜ 0，则 d 轴超前U；Uq= 0，则 d 轴与U同相。其中，Uq表示在q轴上电网电压分量，Ud表示电网电压在d轴的分量。该系统采用闭环控制，可以调节PI参数，通过控制Uq= 0来实现输出相位与电网电压相位同步。

图1 SSRF SPLL控制模型示意

假如三相电压不平衡，根据对称分量法，对三相电网电压进行正序、负序、零序分解，则三相电压可以表示为

ω——基波电压的角频率；

根据三相静止坐标系到两相静止坐标系的变换原则，得到两相静止坐标系下电压为

零序分量经过上述两种坐标系的变换后抵消为零，这样抑制了零序分量的作用，则电网矢量在两相静止坐标系下可以描述为

式（4）表明，在αβ坐标系中，电网电压矢量us分解为以ω角速度旋转的正序分量和以-ω角速度旋转的负序分量。对αβ坐标系上的正负序分量进行dq旋转坐标系变换，其中d+1q+1坐标系旋转角度为，d-1q-1坐标系的旋转角度为-。得到电网电压矢量在两种对称旋转坐标系的表达为

式中：

由式（9）（10）可见，在正序dq坐标系下，输出的正序分量变成了直流量，负序分量变成了2ω频率的交流量；在负序dq坐标系下，输出的负序分量变成了直流量，正序分量变成了2ω的交流量。可以看出，若采用SSRF SPLL，在三相不平衡条件下，由于负序分量的作用，系统不能很好地追踪正序分量，这就对该种锁相环起了限制作用。

2 三相不平衡条件下，正负序分离闭环控制分析

在d+1q+1坐标系中，其中的振荡部分的幅值由d-1q-1坐标系中的平均值决定，而在d-1q-1坐标系中，其中的振荡部分的幅值由d+1q+1坐标系中的平均值决定。为了抑制两种坐标系中的振荡分量，这里采用了两种坐标系下的解耦结构。

根据式（11）（12），设解耦计算的变换公式为

图2是d+1q+1坐标系下的解耦部分，d-1q-1坐标系下的解耦原理与前者一致。

为了获取相应的平均值，这里采用低通滤波器（LPF）（一阶）对2ω信号进行滤除，相应表达为LPF（s）=ωf/(s+ωf)。

图2 d+1q+1坐标系下的解耦网络

整理得出整个锁相环反馈控制系统原理如图3所示，从整个原理图可以看出，为了抑制由负序分量带来的中的二次谐波分量，并且使尽可能靠近0值，信号必须通过解耦网络与PI控制器的联合控制，从而消除三相电压不平衡的作用。

图3 正负序分离的锁相环控制模型

3 MATLAB仿真分析

为验证该锁相环的性能与可行性，利用MATLAB Simulink平台搭建该锁相环模型进行仿真验证。

设置参数如下：三相输入电压幅值分别为UA=1 pV，UB= 1.3 pV，UC= 1.3 pV，其中，A 相电压相位初始相位为0°，频率50 Hz，PI控制器参数，比例系数：kp= 180，积分系数：ki= 22 500，滤波器截止频率ωf= 157 rad/s。

对三相不平衡下的锁相环进行仿真，仿真结果如图4所示，A相电压幅值低于B、C两相电压幅值，锁相环输出信号的波形与A相电压波形相位保持一致，说明三相不平衡条件下，锁相环通过正负序解耦消除了负序分量的影响。可以验证在三相电压平衡条件下，该锁相环能完成三相电压正序分量相位的追踪。

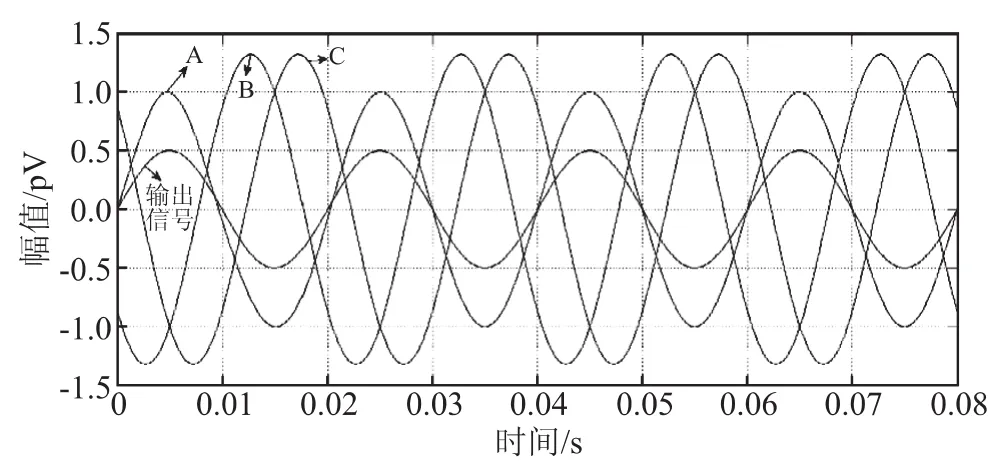
图4 三相不平衡下三相输入电压与输出信号波形

图5为鉴相器输出的正序电压Uq值的波形变化，它的动态响应可以用来判断该锁相环系统的动态响应性能。从仿真结果可以看出，Uq在PI调节器的控制下，最大浮动值为0.32左右。经过大约两个周期的调整即可变为0值并且一直保持下去，由此可以判断动态响应性能良好。

图5 正序分量值的波形

当给三相电压A相注入谐波时，此时A相电压会发生畸变。对模型进行仿真分析，仿真波形如图6所示。结果表明，虽然A相电压畸变，但是输出信号的相位能够实现对A相正序电压的完全锁相。

图6 电压畸变下输入电压与输出信号波形

图7是锁相环输出的相位波形图，可以看出第一个周期，锁相环要经过一个调整过程，相位的变化不是线性变化，在0.02 s时相位并未达到最大值，但是相差不大。在第二个周期结束时相位已经比较准确地进行锁相了，说明在第一周期的系统内部的调整过程中，系统的动态响应并非严重振荡，调节时间大约只有两个周期的时间，可见在电压畸变的情况下，锁相环的稳态性能与动态性能也是非常好的。