高边坡防护中BFRP锚固结构的振动台试验
2020-01-09武志信吴红刚谢显龙
武志信,吴红刚,谢显龙,王 飞
(1.兰州交通大学土木工程学院,甘肃 兰州 730070;2.中铁西北科学研究院有限公司,甘肃兰州 730070;3.中国中铁滑坡工程实验室,甘肃 兰州 730070;4.西部环境岩土及场地修复技术工程实验室,甘肃 兰州 730070;5.西南交通大学地球科学与工程学院,四川 成都 611756)
0 引言
在实际锚固工程中,地震烈度较小的情形下常规预应力锚(索)杆能够表现出良好地抗震效果,可以很好地限制岩体变形,提高边坡的稳定性[1-2]。但是在强震条件下,锚固岩体变形较大,常规预应力锚杆(索)一般难以继续限制其变形,此时锚杆(索)极易因其变形能力不足或瞬时冲击荷载作用下过载而被拉断,引发边坡失稳破坏[3-4],而应用玄武岩纤维塑料增强筋(BFRP)这一新材料代替传统钢筋锚杆(索),可以充分利用其相对钢筋较高地抗拉强度和较低地弹性模量以及较好地应力传递特性和抗震、耐腐蚀、强度高、质量轻、与注浆体黏结性能良好等优点[5-8],能够更好地适应坡体变形的能力,具有明显地边坡抗震效果。
在关于FRP锚杆的直径及灌浆体性能研究方面:BAENA M等[6]、贾新等[9]、刘颖浩[10]等通过研究发现,在一定的锚固长度下,FRP锚杆的黏结强度随锚杆直径的增大而减小,存在着明显的尺寸效应;BENMOKRANE B等[11]通过对AFRP锚杆和CFRP锚杆与不同的灌浆材料之间黏结性能的研究,发现在灌浆料中添加硅粉和砂对提高黏结强度效果最佳,减水剂效果最差;CHENG Y M等[12]通过GFRP锚杆和CFRP锚杆的现场拉拔试验表明,在水泥砂浆中添加膨胀剂可以增大锚杆的锚固性能。在BFRP锚杆与混凝土之间的黏结性能研究方面:赵文等[13]对BFRP锚杆与水泥基质的黏结性能进行了试验研究,并发现水泥基强度越高,黏结强度也越高,且与混凝土的黏结强度大于与砂浆的黏结强度;吴芳[14]通过拉拔试验研究了BFRP锚杆与混凝土之间的黏结锚固性能及黏结滑移本构关系,并与GFRP锚杆、变形钢筋的黏结性能进行了对比分析,并在试验以及己有试验研究的基础上,提出了BFRP锚杆黏结强度理论公式和锚固长度设计建议;沈新等[15]运用18个中心拉拔试件研究了不同螺纹表面玄武岩纤维锚杆与混凝土之间的黏结性能;谢晶晶[16]、黄志怀等[17]、刘纪峰等[18]通过FRP锚杆的强度试验,建议了FRP锚杆与水泥浆之间黏结强度值。在BFRP锚杆支护设计方法研究方面:郭成鹏等[19]对玄武岩纤维杆体BFRP材料和灌浆料的力学性能(抗拉强度)进行了测试,并在此基础上,基于FLAC3D进行了玄武岩纤维锚杆与灌浆料黏结性能的数值模拟分析,并探讨了BFRP锚杆设计方法。
通过上述研究发现,国内外专家对于BFRP锚杆(索)的研究主要集中在其物理力学性能方面,而关于BFRP锚杆(索)应用在边坡支护中的研究还很滞后。鉴于此,为更加细致地研究BFRP锚杆(索)在高烈度地震区高边坡防护中地震响应及其频谱特征,本文以云南省功东高速公路的响水河(K5-K6)全风化玄武岩边坡为典型工点,并采用小波包变换这一同时能够表征地震波在时频两域局部特征能力的数学工具[20],利用其可以对高频信息的信号能够进行更好的时频局部化分析的优点[21],分别对BFRP锚杆(索)及钢锚杆(索)在不同频带下的应变响应情况进行了分析,旨在为BFRP锚杆(索)加固高边坡的动力合理性设计提供科学依据。
1 试验工点概况
试验工点响水河(K5-K6)全风化玄武岩边坡在云南省功东高速公路,项目沿线地形地貌复杂、地质条件变化大、沿线地层破碎,滑塌、崩塌、泥石流等地质灾害频发,水土流失严重,生态环境十分脆弱。同时,该地区受小江断裂带影响,全线地震基本烈度高达Ⅸ度,功东高速沿线地质灾害点及响水河边坡所在位置(图1)。
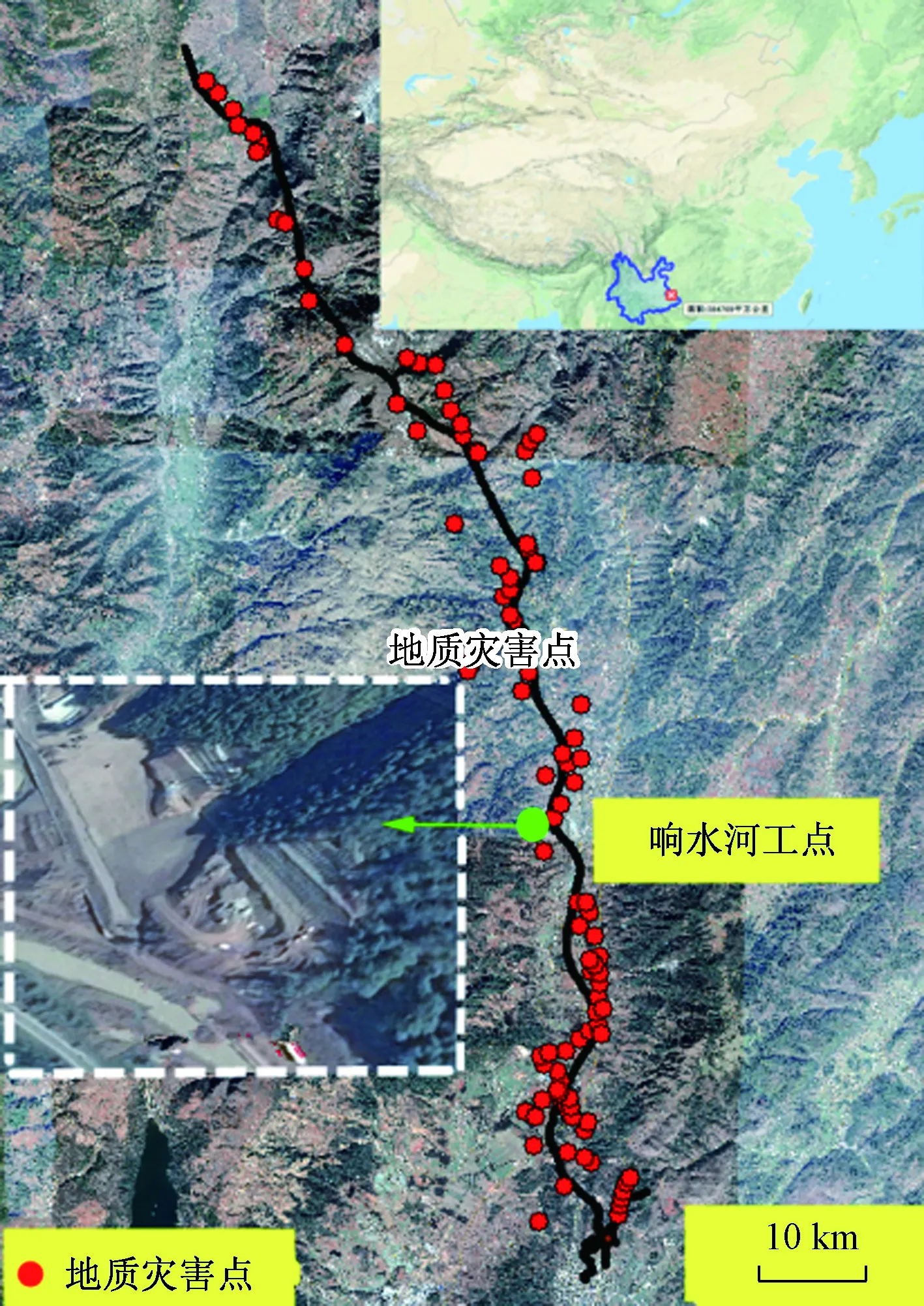
图1 功东高速沿线地质灾害点Fig.1 Geological disaster point along Gong-Dong Expressway
响水河边坡所在坡体地势起伏较大,坡体两端冲沟发育,坡体及冲沟内树木遍布,植被较密,地层岩性为全风化玄武岩。坡体沿基岩有滑动痕迹,滑动方向与线路方向呈30°,可判断此处历史上发生过滑动。左侧冲沟紧挨坡体,右侧冲沟距坡体200 m左右,且右侧距坡体5 m处地形极易发育新的冲沟,对坡体稳定性威胁较大。
该坡坡高36 m,开挖边坡为三级边坡,一级坡高为8 m,二、三级边坡高度均为10 m,设计坡率二级边坡为1∶0.75,三级边坡为1∶1,一级坡设置锚索桩板墙,抗滑桩截面尺寸1.2 m×1.6 m×16 m,二级坡面采用锚索框架防护、三级坡面采用锚杆框架防护。响水河边坡开挖后及支护完成的效果分别如图2(a)、(b)所示。

图2 响水河边坡全貌图Fig.2 Overall view of Xiangshui River slope
2 振动台模型试验设计
本次振动台试验在甘肃省地震局黄土地震工程实验室进行,实验室振动台为VPS~600ES~2型垂直水平双向振动台,振动台尺寸为4 m×6 m。最大负荷质量25 t;最大位移:X向为250 mm,Z向为100 mm;工作频率为0.5~50.0 Hz。
2.1 相似关系设计
根据此次振动台试验条件和目的,相似关系借助因次分析法进行推导,选取几何尺寸l(CL=20)和容重γ(Cγ=1)为基本控制量,其余物理量利用相似“π定理”导出,相似关系如表1所示。
经计算,基于容重相似,弹性模量和黏聚力相似比尺产生的“奇异”较大,在本次试验中模型材料并未完全满足相似比尺的计算要求。但是考虑到本次试验主要研究锚杆(索)的应变,故这些相似材料的次要参数可以忽略[22]。试验工点全风化玄武岩与振动台试验模拟土层的主要物理参数如表2所示。

表1 振动台试验模型相似参数
注:表中p和m分别表示原形量和模型量。

表2 全风化玄武岩与振动台试验模拟土层的主要物理参数
2.2 相似材料与模型制作
根据模型设计参数及多组材料配比试验结果,坡体选择以河砂为主要材料,石膏粉、黏性土为辅助材料,水为粘结材料。为使模型坡体滑动过程连续,本次试验选择用特氟纶薄膜模拟滑带。滑床及滑体部分均以黏性土、河沙、石膏及水为材料制作而成,其质量配合比为5∶10∶1∶1,其中,滑床部分土体压实度较高。抗滑桩采用松木桩模拟,桩长80 cm,悬臂段和嵌固端桩长均为40 cm。试验锚杆(索)分为钢锚杆(索)和BFRP锚杆(索)两种,其直径均为5 mm。
模型箱框架为20 mm厚钢板焊接等边角钢而成,箱体内槽尺寸为2 900 mm(长)×1 400 mm(宽)×1 850 mm(高)。水平振动方向前边为30 mm厚钢板,高为900 mm,后边为50 mm厚聚苯乙烯防震泡沫,长边为20 mm厚透明有机玻璃,可便于观察试验过程中的模型变化情况,振动边界上的减震层采用50 mm厚的聚苯乙烯泡沫。在该试验模型中左幅为抗滑桩+钢锚杆(索)+框架结构对边坡进行支护,右幅为抗滑桩+BFRP锚杆(索)+框架结构对边坡进行支护。制作完成的试验模型如图3所示。
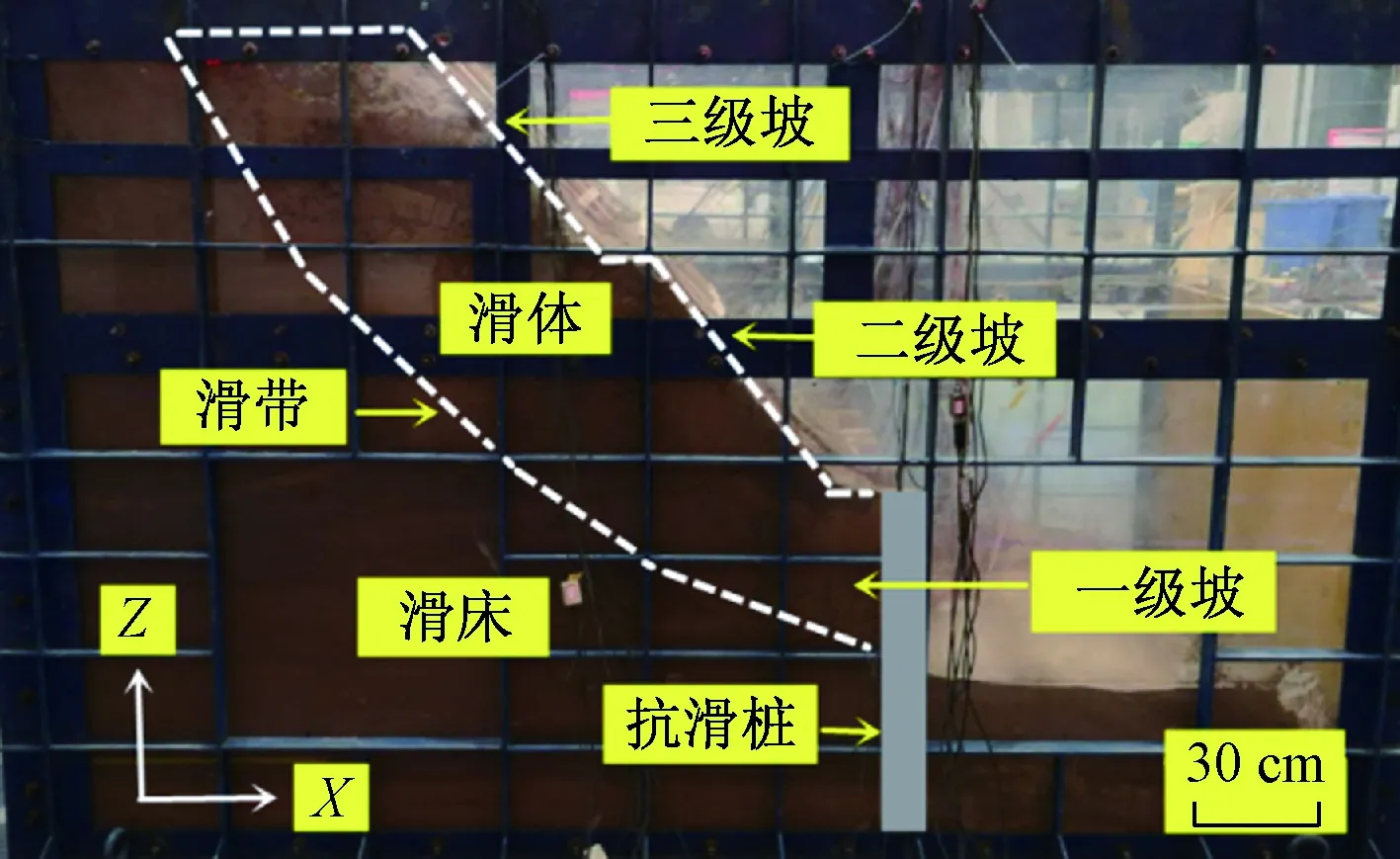
图3 制作完成的试验模型箱Fig.3 The completed test model box
2.3 测试断面及原件布置
考虑到模型箱边界效应的影响,将本次试验所用到的型号为BE120-10A-P100的应变片布置在左右两幅边坡中间一列锚杆(索)上,左幅边坡布置应变片的位置如图4中断面1所示,右幅边坡布置应变片的位置如图4中断面2所示。其中,左右两幅抗滑桩上各布置2列共6根长度为135 cm的锚索,二级坡上各布置3列9根长度为135 cm的锚索,三级坡上各布置3列9根长度为60 cm的全长锚固锚杆,左右两幅坡体中抗滑桩及锚杆(索)的布置形式如图5所示。
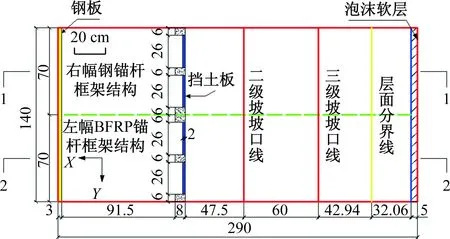
图4 左右两幅边坡中应变片布置示意图(单位:cm)Fig.4 Schematic diagram of strain gauge layout in the left and right slopes (unit: cm)
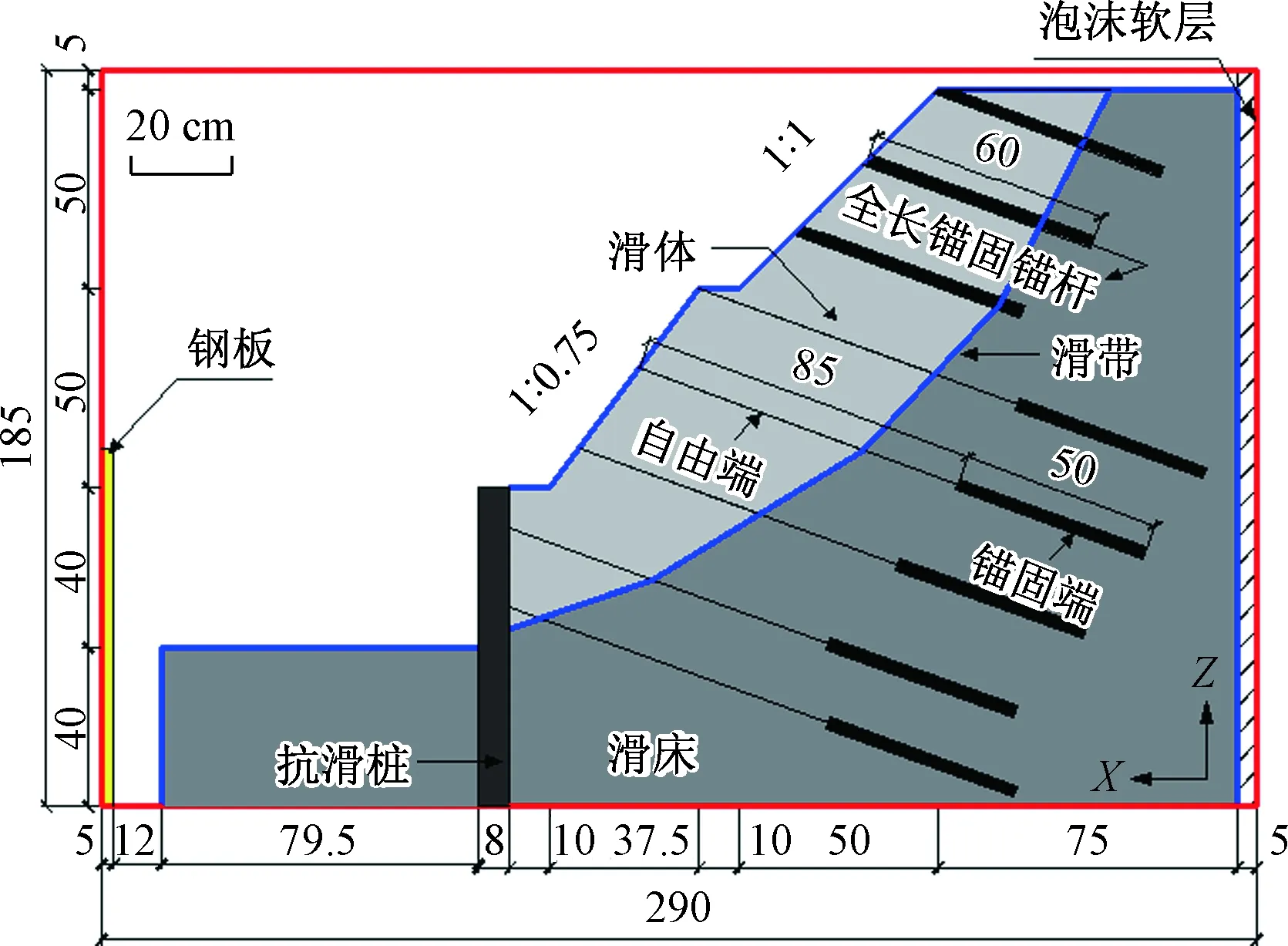
图5 模型结构示意图(单位:cm)Fig.5 Schematic diagram of model structure (unit: cm)
2.4 加载制度设计
由于水平地震是诱发滑坡、导致支挡结构破坏的主要原因[23],因此在该振动台试验中采用EI-Centro波进行X方向的加载方式,加载制度如表3所示。本文主要研究EI-Centro波在X向加载方式下,钢锚杆(索)及BFRP锚杆(索)的响应情况。锚杆(索)应变时程曲线如图6所示。考虑到波长的时间压缩太大会造成地震波的频谱成分更为复杂的原因,故本文地震波并未按照相似体系进行压缩[24]。
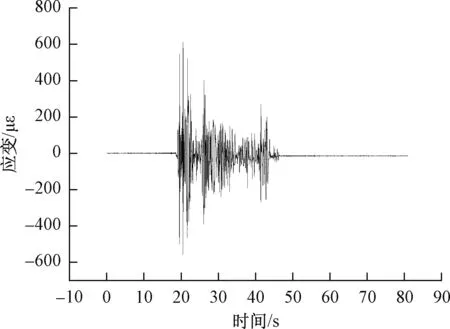
图6 EI-Centro波应变时程曲线Fig.6 EI-Centro wave strain time history curve
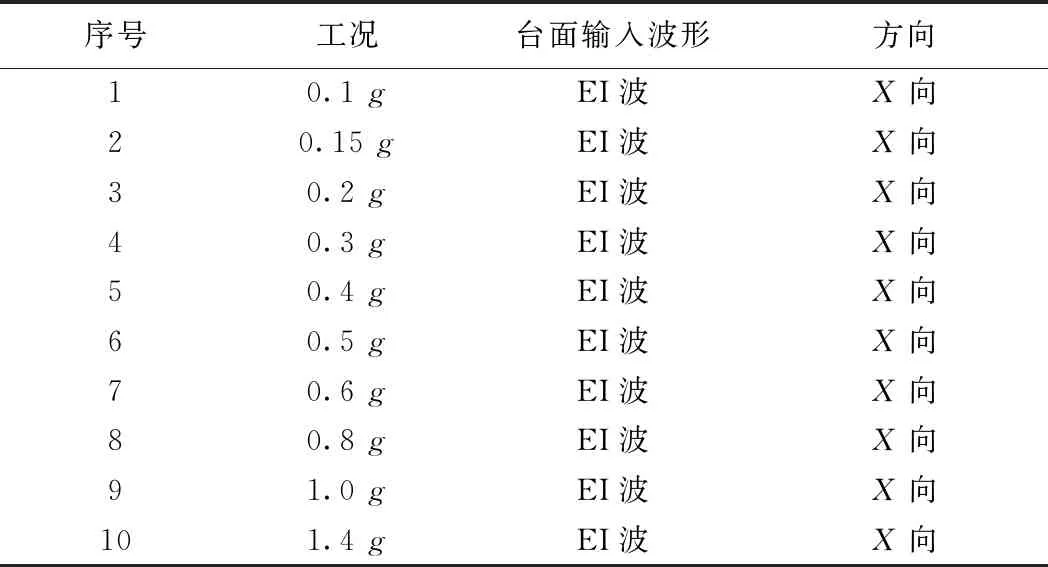
序号工况台面输入波形方向10.1 gEI波X向20.15 gEI波X向30.2 gEI波X向40.3 gEI波X向50.4 gEI波X向60.5 gEI波X向70.6 gEI波X向80.8 gEI波X向91.0 gEI波X向101.4 gEI波X向
3 试验现象分析
按照表3中的加载制度对试验模型进行逐级加载,在加载工况1后,试验模型未发生明显变化,随着试验加载制度的升级,加载到工况2时,左幅钢锚杆(索)侧边坡坡肩位置发生了土体震陷现象,较粗的土体颗粒从碎石的空隙中掉落下来,形成了明显的粗颗粒堆积现象,如图7所示。

图7 工况2作用下土体震陷现象Fig.7 Seismic subsidence of soil under working condition 2
加载到工况5之后,右幅BFRP锚杆(索)侧坡顶滑带埋设位置出现了两条粗细不一的横向裂缝,经测量发现该横向裂缝距离模型箱后壁的位置大约为28 cm,如图8(a)所示。其中较细的横向裂缝长度约为30 cm,较粗的横向裂缝长度为20 cm左右,且这两条横向裂缝有贯通趋势,如图8(b)所示。分析其产生的原因是由于在水平向地震波的张拉作用下,使得坡体在顶部滑带埋设位置出现了裂缝。

图8 工况5作用下坡顶横向裂缝图Fig.8 Transverse crack diagram of slope top under the action of working condition 5
在工况6的地震波作用下,右幅BFRP锚杆(索)侧坡顶位置之前出现的两条横向裂缝贯通为了一条长度约为70 cm的横向裂缝,且裂缝宽度也有所增加,如图9(a)所示。同时,在左幅钢锚杆(索)侧滑带位置处出现了斜向裂缝,分析其原因是地震波的剪切作用所造成的,如图9(b)所示。

图9 工况6作用下坡体变形图Fig.9 Deformation of slope under action of working condition 6
在工况7水平地震波的张拉作用下,使得左幅坡顶滑带位置处出现了一条长度约为50 cm的横向裂缝,如图10(a)所示。同时,在右幅BFRP锚杆(索)侧二级坡坡面位置出现了一条斜向裂缝,其现象如图10(b)所示。

图10 工况7作用下坡体变形图Fig.10 Deformation diagram of slope under action of working condition 7
加载工况8后,使得之前左幅坡体在滑带附近位置出现的斜向裂缝继续发育,长度发生了明显地增长,如图11(a)所示,而与该位置相对应的右幅坡体滑带附近位置未见明显裂缝产生,如11(b)所示。分析其原因是由于BFRP锚杆(索)具有较高的抗拉强度和较低的弹性模量,从而使得锚杆(索)与边坡在一定范围内能够协同变形,故右幅坡体滑带附近位置未见裂缝产生。

图11 工况8作用下坡体变形图Fig.11 Deformation of slope under action of working condition 8
加载工况9后,左右两幅边坡在坡肩位置均出现了土体滑落的现象,从图12中可以看出右幅边坡钢锚杆的外露长度明显要大于左幅边坡BFRP锚杆的外露长度,且相较于左幅BFRP锚杆而言右幅坡体中间的钢锚杆出现了显著地弯曲现象,如图12中红色圆圈所示,从而可以说明BFRP作为一种柔性结构,在地震作用下能够对边坡的变形起到有效地抑制作用。

图12 工况9作用下坡肩土体滑落Fig.12 working condition 9 acted on the soil mass sliding down the slope shoulder
4 试验结果分析
本次试验对工况3、工况6、工况9地震波作用下,左幅边坡及右幅边坡中钢锚杆(索)和BFRP锚杆(索)的应变峰值的分布规律进行了对比研究。并通过小波包工具主要对工况6下钢锚杆(索)和BFRP锚杆(索)的应变频谱特性进行了分析,研究了两者的应变值在不同频段内的变化规律。其中,所要研究的锚杆(索)在左右两幅边坡中各选取3根,从模型底部朝顶部方向,选取桩上第二根锚索定义为下锚索、二级坡上第三根锚索定义为中锚索、三级坡上第三根锚杆定义为上锚杆,其示意图如图13所示。且将左幅边坡中选取的三根锚杆(索)靠近尾部处的应变片定义为A’-1,将靠近端部处的应变片定义为A’-2;将右幅边坡中选取的三根锚杆(索)靠近尾部处的应变片定义为A-1,将靠近端部处的应变片定义为A-2,选取右幅边坡中锚杆(索)为例来说明测点布置情况,如图14所示。
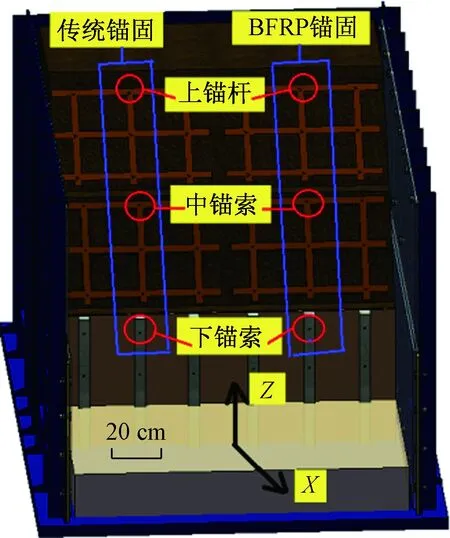
图13 锚杆所对应的位置Fig.13 The position corresponding to the bolt
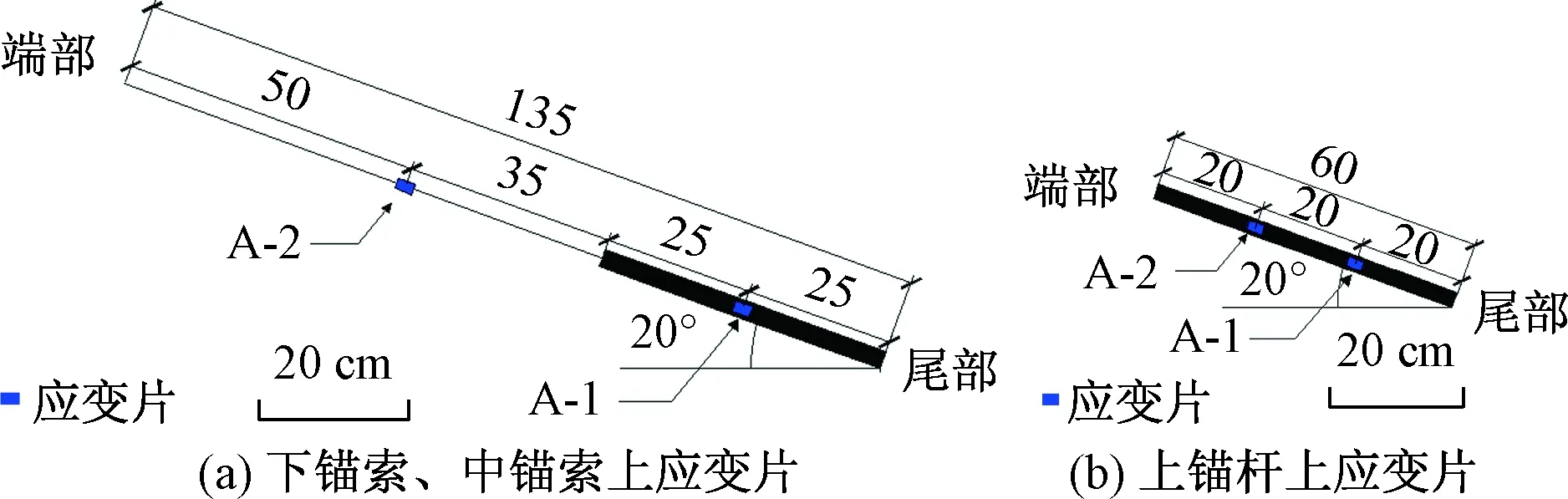
图14 右幅边坡中应变片布置位置Fig.14 Strain gauge placement in right slope
4.1 钢锚杆及BFRP锚杆应变峰值的对比分析
工况3、6、9分别为水平向加载的0.2g、0.5g和1.0g的EI地震波,做出三种工况下钢锚杆(索)及BFRP锚杆(索)分别在尾部及端部处的应变峰值分布图(图15~16)。
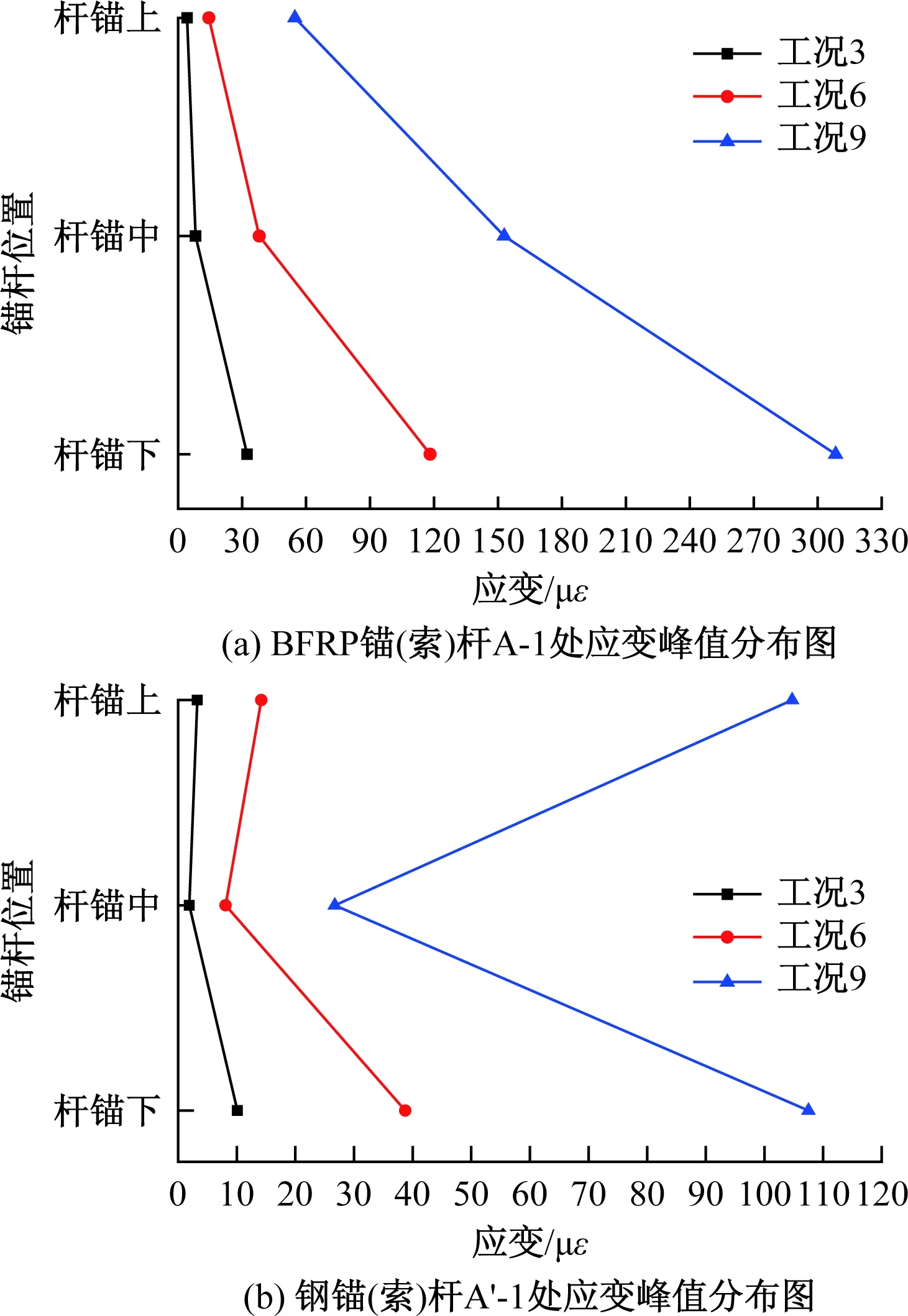
图15 锚杆尾部处应变峰值分布图Fig.15 Strain peak distribution diagram at bolt tail
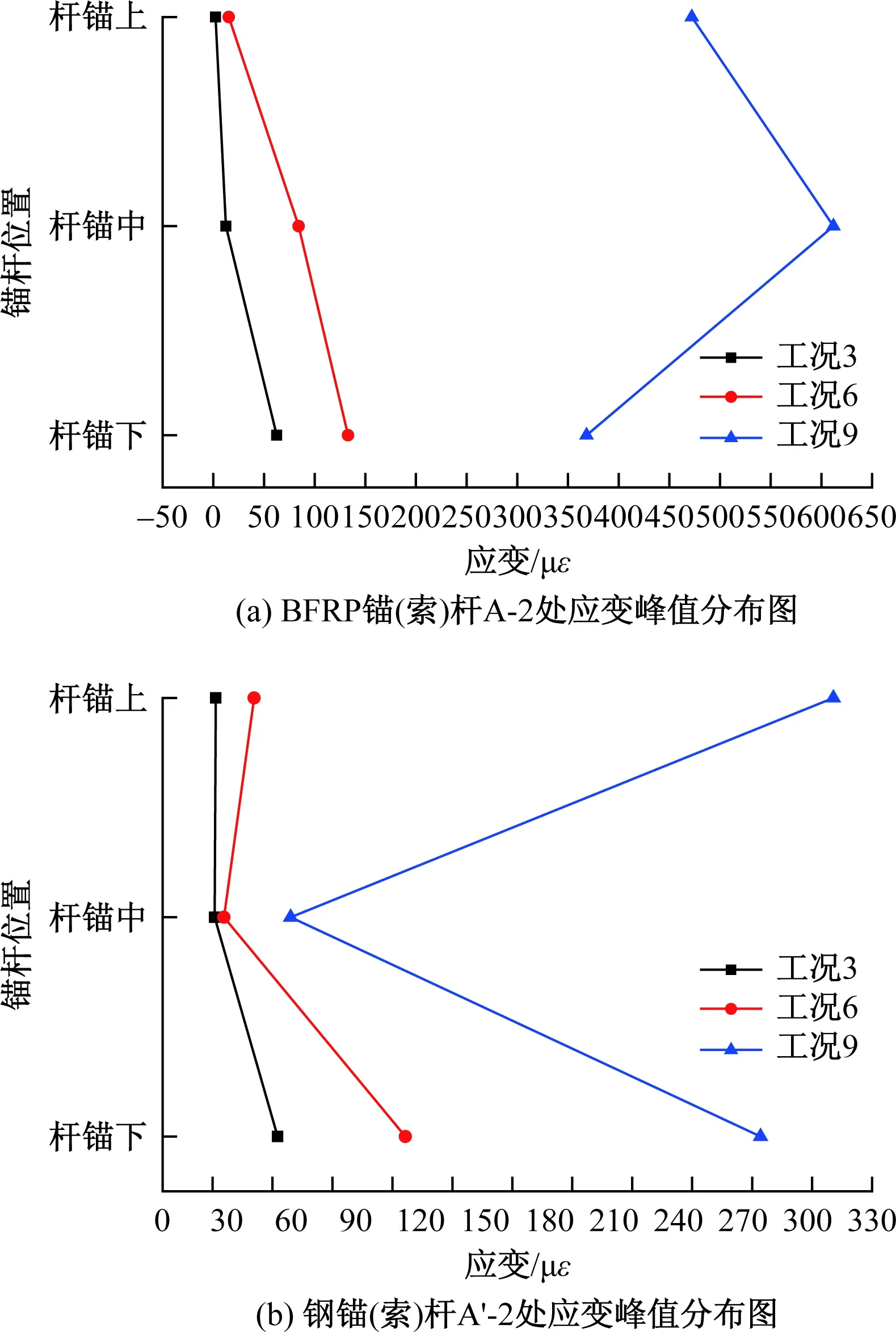
图16 锚杆端部处应变峰值分布图Fig.16 Strain peak distribution diagram at bolt end
从图15(a)可以看出,在三种工况的地震波作用下,对BFRP锚杆(索)而言,A-1处各层的应变随加载量级的增大而增长。下锚索A-1处应变的增长要明显快于中锚索及上锚杆A-1处应变的增长情况,曲线走向近似为斜线。分析其原因是因为BFRP作为一种柔性结构,在振动过程中上锚杆与中锚索能够起到与土体协同变形的效果,所以使得上锚杆与中锚索A-1处受力较小,故其应变也较小。而下锚索由于受到抗滑桩的约束作用,又承受的土体压力较中锚索与上锚杆的大,所以下锚索A-1处应变值最大。
从图15(b)可以看出,钢锚杆(索)A’-1处的应变具有下锚索应变值最大、上锚杆次之、中锚索应变值最小的特点,曲线表现为“K”形,且这种趋势随着加载制度的增大而愈加明显,其主要表现为上锚杆A’-1处应变值增长较快。其应变值分布规律跟BFRP锚杆(索)A-1处应变值的分布规律截然不同,分析其原因是在振动的过程中,坡体下部土体及上部土体变形较大,而钢锚杆(索)作为一种刚性结构,不能很好的随同土体一起变形,故才会出现下锚索和上锚杆A’-1处应变较大的情况。
从图16(a)可以看出,对BFRP锚杆(索)A-2而言,当加速度峰值较小时,其应变分布规律同A-1处的应变分布规律相似,即下锚索A-2处的应变值最大、中锚索次之、上锚杆应变值最小。但是当加速度峰值增大到一定程度后,曲线形状发生明显地变化,表现为反“K”形。例如在工况9的地震波作用下,中锚索的应变值最大,且上锚杆的应变值比下锚索的应变值大,分析其原因是由于随着加载工况的增加,BFRP锚杆(索)与土体的协同变形能力受到了限制,右幅BFRP侧坡体的变形主要表现为坡体中部及上部土体的变形。
由图16(b)可得,钢锚杆A’-2处应变的分布规律同A’-1处的分布规律相似,即具有下锚索应变值最大、上锚杆次之、中锚索应变值最小的特点,曲线表现为“K”形,且这种趋势随着加载程度的增大而愈加明显,其变形原因同A’-1处的相同,此处不再复述。
4.2 地震波的小波包变换及锚杆(索)应变的频谱分析
4.2.1地震波的小波包变换
小波变换是一种时间-尺度分析方法,在时间、尺度(频率)两域都具有表征信号局部特征的能力,具有多分辨率分析的特点。小波包变换是基于小波变换的进一步发展,能够提供比小波变换更高的分辨率,解决了分析信号低频部分时间分辨率差而高频部分频率分辨率差的问题[22]。
鉴于此,本文选取小波函数中具有良好地近似对称性、光滑性及紧支撑性[26],在地震等非稳态信号的分析中具有明显优势的db3函数作为本次振动台试验的小波基函数。且依据Shannon采样定理[27],将本次试验中加载的EL-Centro进行3层分解,共得23=8个小波包,则每个频带的宽度为50/8=6.25 Hz,对应的最低频带为0.1~6.26 Hz,其中,各频带对应的频率范围如表4所示。
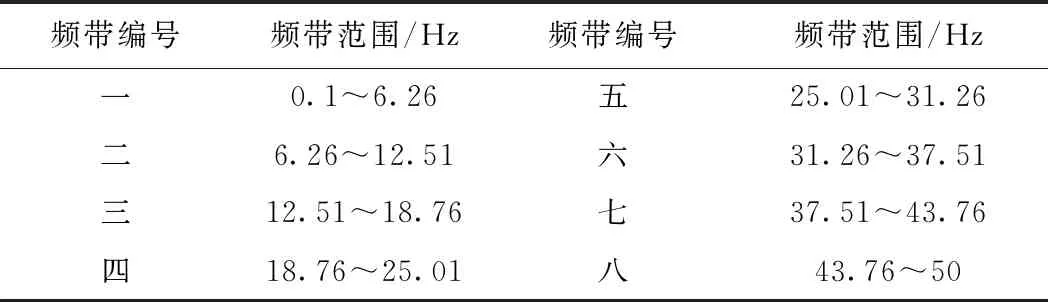
表4 各频带频率范围

图17 钢锚索与BFRP锚索在端部及尾部处的应变小波分量图Fig.17 The strain wavelet component diagram of steel anchor cable and BFRP anchor cable at the end and tail
4.2.2锚杆(索)应变的频谱对比分析
由上述分析可知,钢锚杆(索)及BFRP锚杆(索)的应变值基本上都是下锚索处的最大,故为了分析不同频段地震波的激励下,边坡中钢锚杆(索)及BFRP锚杆(索)应变的响应情况,选取工况6下0.5g的EI波为例,对左右两幅边坡下锚索上应变时域曲线进行小波包分解,作出的小波包分解结果如图17所示。
本文将12.51 Hz以下的地震波均视为低频波,则由图17可得,对左右两幅边坡下锚索上测点A-2、A-1及A’-2、A’-1而言,对应变起影响作用的主要频段为第一频带(0.1~6.26 Hz)和第二频带(6.26~12.51 Hz),土体对于高频(12.51 Hz以上)地震波的吸收比较明显。
同时可以看出,不论是对钢锚索还是对BFRP锚索各频段的应变幅值变化情况而言,锚索端部处的应变值均要大于尾部处的应变值。而且可以得到,在同一测点处,BFRP锚索上的应变值要大于钢锚索上的应变值,这种现象是由于BFRP锚索具有较好的柔性而造成的。综合对比钢锚索及BFRP锚索两个测点处的应变值可以发现,BFRP锚索在端部A-2处的应变值最大,且分别要比BFRP锚索A-1、钢锚索A’-2、钢锚索A’-1处的应变值大1.23、1.41、3.92倍。
由于其他工况的地震波经小波包分解后所得规律跟工况6的相类似,为节省篇幅,此处不再一一列出。
5 结论
通过本次大型振动台试验,对左右两幅边坡中钢锚杆(索)及BFRP锚杆(索)的应变峰值分布规律进行了分析,并利用小波包工具对工况6中加载的EI波进行了分解,且对各频段地震波作用下应变响应及其频谱特性进行了研究,所得结论如下:
(1)从试验现象分析来看,对比钢锚杆(索)及BFRP锚杆(索)分别对边坡的支护效果可以发现,BFRP锚杆(索)与坡体协同变形的效果更加明显。
(2)对钢锚杆(索)及BFRP锚杆(索)对应测点而言,BFRP锚杆(索)上的应变值均要大于钢锚杆(索)上的应变值,且单独对钢锚杆(索)及BFRP锚杆(索)而言,锚杆(索)端部处的应变值均要大于锚杆(索)尾部处的应变值。
(3)对左右两幅边坡下锚索而言,BFRP锚索A-2处的应变值最大,且分别要比BFRP锚索A-1、钢锚索A’-2、钢锚索A’-1处的应变值大1.23、1.41、3.92倍;
(4)对左右两幅边坡下锚索上测点A-2、A-1及A’-2、A’-1而言,对应变起影响作用的主要频段为第一频带(0.1~6.26 Hz)和第二频带(6.26~12.51 Hz),土体对于高频(12.51 Hz以上)地震波的吸收比较明显。
