参数化设计在老年人户外游憩空间规划中的应用研究①

曹 田 李亚军（南京理工大学 设计艺术与传媒学院，江苏 南京 210094）

引 言

户外游憩活动是人们在户外公共空间中进行休闲活动的总称，[1]城市公园、乡间景观、旅游景区等为人们游憩活动提供服务的场所称为户外游憩空间。近年来，我国老年人口数量猛增，这为户外游憩空间增添了不少压力，也使得户外游憩空间的“适老化”问题变得越来越紧迫。

当前，“适老化”已经成为户外游憩空间规划与设计的一个重要趋向。但是，“适老化”的方法大多停留在传统的社会调研和经验积累的层面，主观性和模糊性较强，难以为老年人的多样化、个性化的游憩活动提供“精准”服务。

参数化设计是近年来国内外兴起的一种新的设计潮流。通过计算机程序的模拟，参数化设计可以打破设计师与用户之间的矛盾，以精准的、动态的方式来满足用户的多样需求。有鉴于此，参数化设计可能为解决城乡户外游憩空间的“适老化设计”问题提供一个突破口。

一、参数化设计在老年人户外游憩空间规划中的应用可行性

（一）参数化设计的主要特点

算机算法来模拟老年人的游憩活动，再以此决定设计，形成“自下而上”的设计模式。

2）参数化设计中，对老年人游憩需求的分析和运算是由计算机软件来完成的，提高了设计的效率。

3）通过算法逻辑的建立和参数数据的控制，参数化设计对老年人的游憩需求进行精确描述与量化生形，增强了规划设计的可靠性与可控性，对景观节点的可达性、活动场地的联系性等问题给出较为精准的答案。

4）参数化设计直观、客观地描述规划设计过程的每一个步骤，当老年人的需求发生变化时，可以便捷地修改设计，实现设计的定制化。

（二）算法的适用

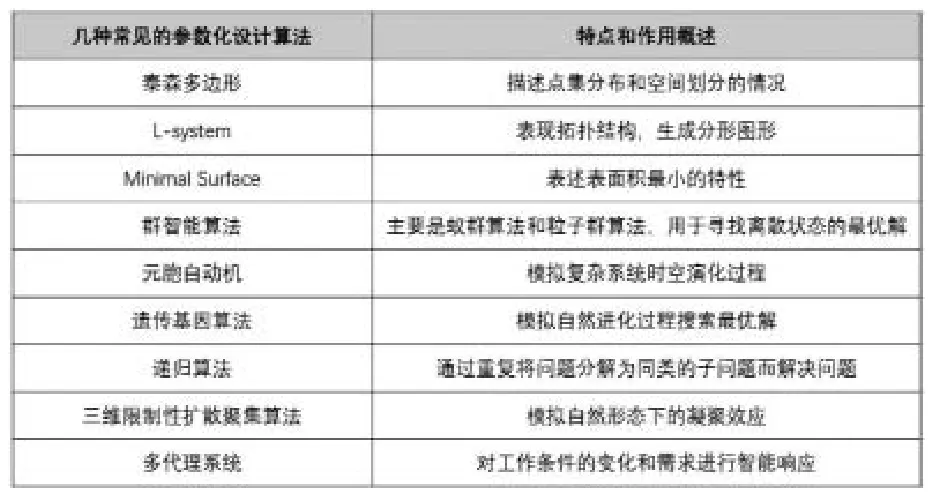
表1 建筑和景观领域常见的算法及特点 图片来源：作者自绘

对于老年人户外游憩空间规划来说，参数化设计方法有以下几个特点：

1）参数化设计以老年人的需求为主导，运用计

算法是参数化设计的核心问题，决定了设计的研究方向、演变途径、设计周期以及成果的生成表达。[2]参数化设计包含多种算法，其特点和作用各有不同（表1）老年人户外游憩空间规划设计有多个方面，可能涉及到空间关系分析、视域分析、路径优化等，因此会用到泰森多边形、元胞自动机、遗传基因等多种算法。

1.参数化设计的技术平台

参数化设计大多是依托建模软件来实现，如Rhinoceros、MAYA、3DMAX等，计算机脚本工具为参数化设计提供了算法运行的平台，有Grasshopper、Rhino script等。[3]本 课 题 运 用Rhinoceros和Grasshopper这两个软件平台进行研究。

2.具体的应用面

参数化设计在老年人户外游憩空间规划中的应用，可以分为两方面。一方面是老年人游憩方案的设计，即通过输入老年人的个性化需求参数，进行算法的模拟，为其定制最为合理的游憩方案。另一方面，是通过算法模拟来检验游憩空间某几个方面的适老性（如游览路径、可视域、植物配置等是否适合老年人游憩），并指导游憩空间设计的优化。这两方面应用的基本流程是一致的，都是通过参数输入和算法模拟，计算出最优解。

二、基于参数化设计的老年人户外游憩空间规划策略

参数化设计往往先从服务对象入手，建立服务对象与设计的联系与规则，进而形成算法逻辑，按照逻辑生成设计形态。有鉴于此，基于参数化设计的老年人户外游憩空间规划的策略如下。

（一）设计需求的量化采集

1.量化描述

以数据的方式来描绘老年人的活动能力和活动偏好。比如，以如厕间隔的平均时间、平均步行速度、单次最大步行距离（指每次休憩间隔的最大步行距离）、步行总距离、平均休憩时间（指多次休憩时长的平均值）等多个数据来描述某位60～70岁男性老年人的游憩活动能力和活动偏好。

2.分情况采集

在不同的情况下，游憩空间内的老年人可能有不同的游憩目的，需求和偏好也有不同。以一日时间的变化为例，早晨和傍晚的游憩空间内以晨练者为主，对锻炼场地的条件较为关注。而白天其他时间，游憩空间内的游客和坐憩者占大多数，他们对游览路线、观景效果和服务设施等方面的需求就要高于晨练者。同样，不同的天气、季节等因素都会对需求数据造成影响。

（二）参数数据的筛分关联

1.筛分与关联

采集得到的数据需要进行筛分，与游憩空间的设计要点进行关联，才能成为参数化设计可用的参数。如，老年人的单次最佳步行距离可能与景观组团的构成、景点分布布局、游览路线的选择等设计要点有密切联系，而老年人的感知范围则与游憩空间的尺度、景观的围合状态、活动场地的关联性等设计要点息息相关。

2.影响因素的综合考虑

游憩空间中的水体、植被、建筑物等，都可能对老年人的游憩活动产生影响。在需求数据与设计要点进行关联时，要充分考虑到这些因素的影响。比如，在某些值得驻足观赏的景观节点，老年人的平均步速可能会变慢，平均休憩时间会变长，单次步行的最大距离也可能变长。

（三）算法逻辑的科学构建

1.算法逻辑符合计算机的运行规律

计算机软件的运算逻辑与人类逻辑有所不同，编写算法时，需要将人类的逻辑转化成计算机逻辑。比如，人类可以在10处景观节点中轻易地选中某个节点，但计算机的逻辑可能是：先将10个景观节点进行编号，再根据编号选中某个节点，或者根据该节点的位置特征来进行选择。

2.算法逻辑涵盖所有情况

选择某种算法进行规则的构建时，要涵盖老年人游憩活动的所有情况。譬如，以老年人的最大感知范围来检验景观组团的可感知性，需要将老年人的视觉、听觉、嗅觉等感知能力都考虑在内。这是因为，在有些空间中老年人的视觉感知较强，而有些空间中则听觉或嗅觉感知较强。

（四）规划形态的动态生成

1.审视与取舍

目前，参数化设计还处于“弱人工智能”阶段，计算机只能根据人工编写的算法程序进行运算，尚不能进行独立思考和自主研判。计算机计算出的规划形态可能有多个解，这些解符合计算机的算法逻辑，却不一定与现实情况相匹配。因此，设计师需要结合各种因素，进行审视、判断和取舍，最终确定规划方案。

2.修改参数以获取不同条件下的最优解

参数化设计的特点之一是可以修改参数，以适应不同的设计条件。参数的修改是有界限的，界限可能是现实条件下的极值，也可能是计算机运算能力的极限，超过界限，则设计方案不成立。在界限内修改参数，可以得出相应情况下的最优解；若是连续地变动参数，相应的规划形态能够进行实时的变化，实现动态的、可变的规划设计。

三、参数化设计在景区游憩空间规划适老性问题上的实证研究

当前，很多旅游景区同时也是老年人的游憩场所。不少景区的游憩空间具有一定的适老性，对老年人有较大的吸引力。但是，其适老性未能得到验证，难以为其他景区的适老化改造或建设提供令人信服的经验借鉴和策略启示。鉴于此，本课题对景区游憩空间的适老性进行实证研究，验证参数化技术在该问题上的应用。

本课题以江苏省扬州市瘦西湖景区（以下简称“瘦西湖”）为例进行分析。瘦西湖的前身是明清时期扬州盐商在城北郊区所建的诸多园林景观，经过数百年的演变和扩充，这里逐渐成为享誉国内外的风景名胜区。瘦西湖是较为典型的历史文化景区，人们的游憩活动以参观游览和情景体验为主。本课题选择最能影响人们游憩质量的游览路径作为适老性研究的切入点。

传统园林景观的营造，十分讲究游览路径的规划与设计，有“一步一景、移步换景”之说。游览者在移动的过程中不断地感受到景观的变换，多重景观的共时性和历时性变化，带给游览者丰富的观景享受，如，时而山楼凭远；时而竹坞寻幽；时而夜雨芭蕉；时而晓风杨柳。换言之，让游人在有限的时间和精力内，尽可能获得丰富而有节奏的景观感知体验，是传统园林游览路径设计的基本原则之一。

根据前期调研，瘦西湖现有的游览路径符合上述基本原则，游客对游览路径中的景观感知体验比较满意。但是，老年游客是特殊的游览人群，老年人的身体条件和感知能力都比青壮年游客要弱，就要考虑现有的游览路径规划是否适合老年人的需求？

（一）老年人景观感知的参数与逻辑单元

老年人对景物的感知主要分为视觉感知、听觉感知和嗅觉感知三方面，且三方面的感知角度都是360度。因此，将老年人的景观感知域设定为一个圆，圆心即老年人，半径是老年人的最大感知半径。将某一个时刻老年人的视觉最大感知半径设定为a，听觉最大感知半径设定为b，嗅觉最大感知半径设定为c，老年人的综合最大感知半径为x，则x为该时刻a、b、c的最大值，即：

x=max{a，b，c}

游览路径中，受到不同因素的影响，如建筑的遮挡、风向的变化、声音的屏蔽等，a、b、c是在不断变化的。考虑到老年人对景观的感知是三方面的综合，景观与老年人的距离只要小于三方面数值的最大值X，即可认为老年人对该景观具有可感知性。如，由于植物的遮挡，老年人看不到某处景观，但能够听到景观传来的悠扬音乐，或闻到景观的香味，仍然可以认为老年人感知到了该处景观。基于此，设定景观与老年人的直线距离为Y，老年人对景观的可感知性为α，则有：

当Y＞X，则α=false

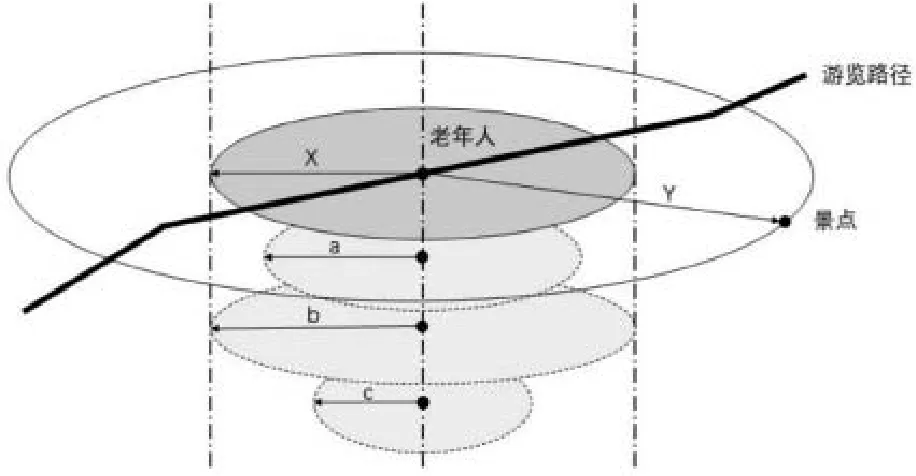
图1 老年人感知域的几何模块 图片来源：作者自绘

当Y≤X，则α=true

上述两个公式共同组合成一个逻辑单元。根据前期对老年人户外感知能力的调查，以100m作为X的参数值，即可绘制出老年人感知域的几何模块（图1）。

（二）景点布局的参数化分析

瘦西湖景区景点众多，游览路径也有多条，对这些景点的分布布局进行参数化分析，可为老年人理想的游览路径提供一个选项集。

将瘦西湖的主要景点标注在地图上，共有62处，组成集合P（图2）。这些景点中，相邻的三个点连接成三角网M（图3）。这些三角形的外接圆圆心O，是到三角形三个顶点等距且最近的点，共有126个，组成集合O（图4）。综上，则有：

P={P1，P2，P3……P62}

O={O1，O2，O3……O126}

图2 景点集合P

图3 三角网M

图4 三角形外接圆圆心集合O

可以认为，当老年人位于这些景点P或位于外接圆圆心O时，最可能感知到这些景点。换言之，将景点P与外接圆圆心O的集合进行合并组成集合PO，则有PO=P∪O。集合PO中的点，即是老年人游览路径的必经点（图5）。

瘦西湖景点的分布是不均匀的，有些景点距离较近，形成组团，有些则较远。这意味着在老年人有限的感知能力、行动精力和时间安排下，不可能将所有的景点都饱览一遍。因此，需要计算出最省时省力，又能在有限感知域内感知最多景点的理想路径。该路径即在集合PO中产生。

图5 景点集合P与外接圆圆心O的并集PO 图片来源：作者自绘

图6 景观到老年人的直线距离集合Y 图片来源：作者自绘

图7 三角网M’ 图片来源：作者自绘

图8 三角网m 图片来源：作者自绘

（三）老年人理想游览路径的生成

根据老年人的感知参数与几何模块计算老年人理想游览路径的关键，在于将老年人的综合感知半径X与景观到老年人的直线距离Y进行比较。将外接圆圆心O分别与三角形的顶点相连，可在每个三角形内获得三条连接线。这些连接线即是景观到老年人的直线距离Y。将这些连接线提取出来，共有359条线，组成集合Y（图6），则有：

Y={L1，L2，L3……L359}

计算Y集合中每个元素的长度值，将X参数值（100m）与Y集合中的各个长度值进行比较，筛除Y集合中长度值大于X的参数值的项，剩下65项，这些项所对应的点即是老年人理想游览路径的必经点，设为集合O’。

将集合P与集合O’再次合并，形成集合PO’，并将该集合中的点相互联系，形成三角网M’，老年人理想游览路径即在该三角网M’中产生（图7）。

虽然从理论上说，三角网M’中任意一条线段都是符合老年人感知能力的游览路线，但现实中有很多线段则是不成立的，比如有些线段过长，有些线段已经超出了瘦西湖景区的边界，有些线段跨越了水面等。因此，对三角网M’需要再进行一次筛除，除去不合理的线段，得到新的三角网m（图8）。

在三角网m中，输入老年人游览路径的起点（南大门）和终点（北大门），进行最短路径的计算，即可得到老年人理想的游览路径（图9）。改变起点和终点，或者修改老年人的综合感知半径数值，都可以计算出不同情况下的最优解。如，将起点和终点设为瘦西湖东大门和西大门时，得到新的理想游览路径（图10）；若起止点不变，减小老年人的综合感知半径数值至60m时，理想游览路径如图所示（图11）。

需要注意的是，这里计算出的最优解仍然需要进行人工修正和调整，才能最终成为可行解。

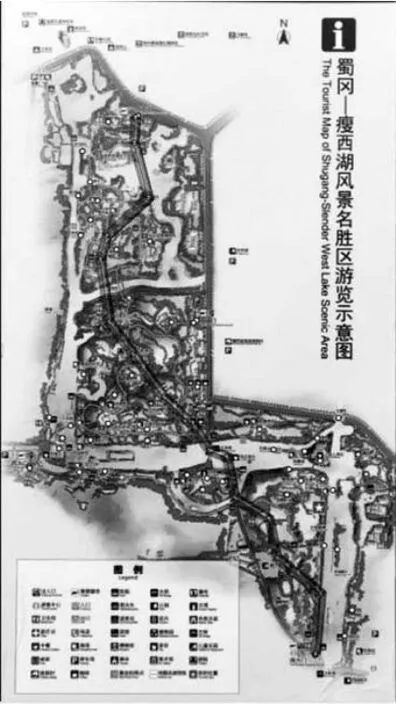
图9 游览路径1

图10 游览路径2

图11 游览路径3图片来源：作者自绘

（四）理想游览路径与现有路径的比较分析

将上述计算所得的可行解与现有的规划设计进行比较，可以得出以下结果：

（1）检验现有游览路径的合理性。经过比较，瘦西湖现有的游览路径与老年人的理想路径总体接近，瘦西湖现有的游览路径具有合理性，值得其他景区借鉴。

（2）分析现有游览路径与理想路径的差异之处。瘦西湖现有的游览路径与老年人的理想路径有部分差异。当起点和终点分别设置在瘦西湖南大门与北大门时，路径的差异主要体现在“小金山”景观片区和“熙春台”景观片区。这两个景观片区集中了瘦西湖的一些主要景点，现有的游览路径穿过了这些景点，而老年人的理想路径没有穿过。原因可能是这两个景观片区的位置相对较偏，在有限的体力和时间内，老年人难以顾及这两个景观片区。这是瘦西湖景区游览路径与景观分布在适老性方面存在的问题。

笔者随后在瘦西湖景区中进行了4个小时的现场观察，发现的确有不少老年人选择放弃游览上述两个景观片区，实地观察验证了本课题研究的有效性。

（3）总结现有游览路径规划的经验，为其他景区的设计提供借鉴。分析发现，瘦西湖现有的游览路径能够一次性地串联大多数主要景点，景点在路径上有序列、有节奏地步步呈现，且景点之间的间隔距离总体上较为均匀。这样的设计符合老年人的游览能力和游览偏好，使得老年人乐于徜徉其中。对于其他景区来说，游览路径的规划设计可以吸收瘦西湖景区的经验，避免景点分布的严重不均或游览路径绕路较多，以增强景区游憩空间的适老性。

（五）未来应用面的展望

本课题的研究具有可推广性。通过算法计算、参数化设计，可以为其他类似的问题提供解决方案。譬如，在倡导全域旅游的新背景下，城市的各方面资源都为旅游而服务。城市旅游需要合理的日程安排、路径规划和餐饮住宿调配，通过算法规则的建立，参数化设计可以计算出最符合游客需求的行程安排、最省时省力的路径方案，以及资源整合率最高的餐饮住宿选择，为城市全域旅游的发展提供精准而科学的规划路线设计。

结 语

参数化设计是近年来国内外兴起的数字化设计方法，广泛地应用于地理学、气象学、建筑学等领域。如今，景观园林设计、产品设计等领域也开始运用参数化设计进行创新和创造。但总的来说，参数化设计主要还是用于“造物”。本课题将参数化设计运用于老年人户外游憩空间的规划与设计，是对这种新型的设计方法在人文社会科学领域的一种拓展。虽然参数化设计的应用尚处于起步阶段，还有很多问题亟待解决，但这种精确的、理性的设计已经与传统的“模糊性、经验性”设计区别开来，展现出了较大的理论和实践价值。未来，相信参数化设计将在人文社会科学领域能发挥更加重要的作用。