京张高铁八达岭长城站超大跨隧道变形控制标准研究

2020-01-09刘建友张民庆

铁道标准设计 2020年1期

吕刚,刘建友,张民庆,岳岭

(1.中铁工程设计咨询集团有限公司,北京 100055；2.中国国家铁路集团有限公司,北京 100844)

引言

京张高铁新八达岭隧道全长12.01 km，为单洞双线隧道，标准段开挖跨度13.52～13.82 m，大跨过渡段开挖跨度达32.7 m，是目前国内开挖跨度最大的暗挖铁路隧道，安全风险高，施工难度大。大跨过渡段一共分为11步开挖，每一步开挖都将引起拱顶变形及整体变形，将变形控制在设计允许的安全范围内则是整个隧道施工的关键与难点。

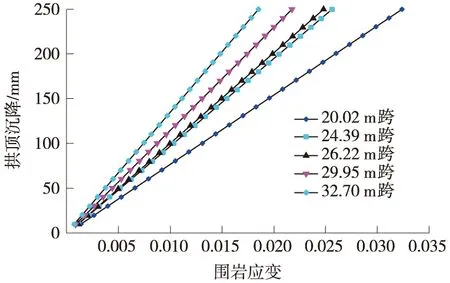
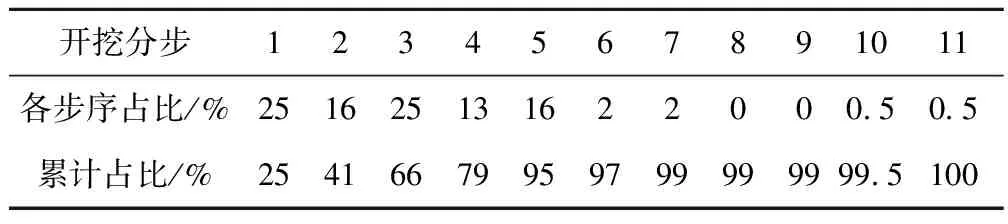
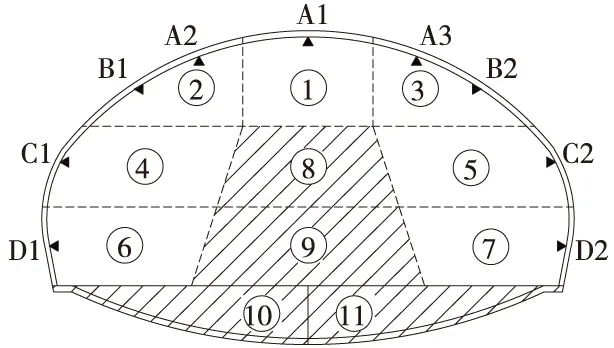
国内外学者对大跨隧道、变形控制进行了相关研究。易小明等[1]通过对厦门市梧村山隧道施工现场全方位的变形监控量测，建立相应的建筑物变形控制标准。刘招伟等[2]对某双连拱隧道施工过程进行现场监测与结果分析，提出了抑制变形的工程措施。瞿万波等[3]根据监测数据，对洞桩法隧道导洞开挖的沉降变形规律进行了分析研究。郑熙熙等[4]以重庆市两江桥渝中连接隧道与解放东路接口工程为依托，分析了隧道施工引起的地表变形规律、影响因素，提出了针对性的设计方案与控制措施。唐晓杰等[5]针对大跨地铁隧道穿越断层的围岩变形与控制问题，采用FLAC3D数值模拟，分析双侧壁导坑工法与CD工法不同组合穿越断层的围岩变形规律与注浆控制效果。郑广顺等[6]基于FLAC3D数值模拟软件，对比分析上下台阶法和CD法施工引起的隧道变形及受力特点，提出了有效的变形控制措施。廖雄[7]以成兰铁路杨家坪隧道分合修过渡段为工程依托，通过理论分析和数值模拟研究该隧道施工变形机理和变形规律，提出了适合该工程的变形控制措施。HOU Fujin等[8]以某城市滨海大跨度隧道为依托，优化分析了岩体的本构计算模型，对隧道施工过程进行了全时空分析，研究表明施工时应控制开挖面前方变形。LI Shuchen等[9]对长城岭大跨超浅埋隧道进行物理模型试验和数值模拟，研究分析了大跨浅埋双连拱隧道的变形规律。毛金龙[10]采用工程类比法和数值模拟分析法，对兰州新区至兰州段大跨新黄土隧道进行研究分析，针对施工过程中出现的隧道沉降变形提出控制措施。何昌国[11]结合现场实测数据并采取数值模拟分析，对成贵铁路四川段大跨隧道的变形特性及变形量进行研究分析，并对隧道预留变形量进行优化。董德智[12]研究了周山隧道的施工工法，提出了软弱围岩大断面隧道的变形控制技术。杜洪新等[13]以全国跨度最大、长度最长的乐疃高速公路隧道为工程背景，采用数值模拟计算，分析了不同初期支护强度下拱顶位移的变化规律。周磊生等[14]采用数值模拟计算，研究分析了CD及CRD开挖工法下超大断面隧道围岩变形控制机制。现行规范QCR9218—2015《铁路隧道监控量测技术规程》制定了隧道断面变形控制的标准，但其针对的是跨度B≤7 m的单向隧道、跨度7 m

以京张高铁八达岭长城站超大跨隧道为研究对象，分析了不同跨度下隧道拱顶沉降与围岩应变的关系，基于开挖过程隧道断面的变形开展了数值模拟与现场监测研究分析，提出了超大跨隧道施工的变形控制标准。本文的研究将对类似超大跨隧道施工变形控制提供参考与借鉴。

1 工程概况

京张高速铁路新八达岭隧道全长12.01 km，八达岭长城站位于新八达岭隧道内，车站中心里程距离隧道进口8.79 km，距离隧道出口3.22 km。车站两端的站隧过渡段，是一个由两线铁路过渡到四线铁路的单跨隧道，最大开挖跨度32.7 m，拱顶埋深62.7～120.0 m。

大跨过渡段洞身主要穿越强-弱风化花岗岩，块状构造，岩体总体上较完整～较破碎，岩质较坚硬，岩块单轴饱和抗压强度为40～60 MPa。大跨段DK68+260～DK68+300出露F2断层，与线路相交角度35°，断层带宽约2 m，带内夹泥，岩体破坏，强风化，为Ⅴ级围岩。大跨段地下水类型为基岩裂隙水，受前期周边辅助洞室开挖的影响，地下水已疏干。

2 超大跨隧道总变形控制标准

制定隧道总变形量控制标准，首先可计算岩体极限应变，其次根据隧道断面和变形关系确定岩体临界变形量，最终提出隧道总变形量控制基准值。

2.1 岩体的极限应变

岩体的极限应变取决于岩石的极限应变和岩体中节理裂隙的分布[15]。当隧道围岩为整体块状结构，岩体中的节理裂隙很少，岩体的极限应变可近似采用岩石的极限应变。根据对大跨段岩石取芯的实验结果，八达岭长城站岩石的极限应变为1.4‰～3.1‰，如图1所示。

八达岭长城站大跨段受F2断层的影响，岩体较破碎，局部岩体夹泥，全～强风化，因此，围岩变形必须考虑节理裂隙的影响。

岩体极限应变计算公式如下

(1)

式中，σmc为岩体的应力，Em为岩体的弹性模量。

岩体强度由E.Hoek提出的广义H-B强度准则计算

图1 八达岭长城站大跨段花岗岩样品应力应变曲线

(2)

式中：mb、s、a为反映岩体特征的经验参数，其中，mb、a为针对不同岩体的量纲为1的经验参数，反映岩体破碎程度，取值范围为0.0～1.0，对于完整的岩体(即岩石)，s=1.0。

岩体弹性模量采用W.S.Gardner提出的经验公式计算岩体的弹性模量

αE=Em/Er=0.023 1RQD-1.32

(3)

式中，折减系数αE为岩体与岩块的弹性模量比Em/Er，为岩体质量指标。根据上式计算得到八达岭长城站岩体的极限应变如表1所示。

表1 八达岭长城站岩体极限应变

2.2 隧道极限变形

为了确定拱顶沉降与隧道开挖跨度的关系，简化隧道计算模型如图2所示。

图2 围岩拱顶临界变形计算模型

(4)

式中，γ为角度∠AHE

(5)

针对八达岭长城站不同断面跨度，选取跨度为20.02，24.39，26.22，29.95，32.7 m的断面开展研究，各断面跨度下的拱顶沉降和围岩应变关系曲线见图3。

图3 不同跨度隧道拱顶沉降与围岩应变关系曲线

由图3所示，当隧道跨度一定时，拱顶沉降和围岩应变呈线性关系，拱顶沉降随着围岩应变的增大而增大；而当围岩应变一定时，随着隧道跨度的增大，拱顶沉降随之增大。

2.3 总变形控制标准

根据岩体的极限应变计算和不同跨度隧道的极限变形，提出针对八达岭长城站大跨隧道的总变形控制标准，如表2所示。

表2 大跨隧道总变形控制标准

3 超大断面隧道分步变形量控制标准

超大断面隧道开挖步序多、周期长[16]，为确保施工安全，必须对每个分步开挖都进行变形量控制。因此，需要对总变形量进行分解，即

S=S1+S2+S3+…+S11

(6)

式中，S为总变形量控制基准值；S1、S2、S3…分别为每分步变形量控制基准值。

八达岭地下车站大跨段隧道共分为11步开挖，如图4所示。因此，将总变形量控制基准值分解为11个步序子变形量控制基准值，从而实现对隧道施工过程的安全控制。

为了确定大跨段隧道各个分步开挖变形量的占比关系，采用数值模拟[17-19]的方法计算大跨段隧道分步开挖引起的变形量，从而得到每个分步开挖引起的变形量与总变形量之比。计算结果如图5所示。

图4 大跨段隧道施工步序

图5 各开挖步序沉降变形占比

根据图5，可将大跨断面11步开挖过程分为成跨阶段、成墙阶段、落底阶段三个阶段，其变形规律如下。

(1)成跨阶段。成跨阶段为大跨段隧道开挖的第1步至第5步，即上层中、左、右洞开挖，中层左、右侧洞开挖。成跨阶段隧道跨度在不断增大，因此开挖引起的沉降变形占比较大，Ⅲ级围岩成跨阶段变形占比达到了总变形量的97%，Ⅳ级围岩达到了95%，Ⅴ级围岩达到了79%。

(2)成墙阶段。成墙阶段为大跨段隧道开挖的第6步和第7步，即下层左、右侧洞开挖。成墙阶段隧道跨度没有增大，但隧道高度逐渐增大。与成跨阶段相比，成墙阶段拱下沉占比明显变小。Ⅲ级围岩成墙阶段变形占比为总变形量的5%，Ⅳ级围岩为7%，Ⅴ级围岩为21%。

(3)落底阶段。落底阶段为大跨段隧道开挖的第8步至第11步，即中、下层核心土，左、右侧仰拱开挖。落底阶段隧道跨度和高度基本不变，因此本阶段沉降变形占比趋近于0，甚至由于开挖卸载作用，隧道会出现向上的隆起变形。

根据以上变形规律，大跨段隧道各分步拱顶下沉占比可采用下列公式计算

(7)

式中，Pi为各分步拱顶下沉变形占比；n1为成跨阶段开挖分步的总步数；n2为成墙阶段开挖分步的总步数。

根据数值模拟计算结果，并充分考虑预应力锚杆、预应力锚索对围岩的加固作用，最终确定八达岭地下车站大跨段隧道拱顶下沉各步序占比控制标准，见表3。

表3 八达岭地下车站大跨段隧道拱顶下沉各步序占比

根据各步序占比，结合总变形控制标准，可制定八达岭地下车站大跨段隧道各步序拱顶下沉控制标准，如表4所示。

表4 大跨段隧道各施工步序变形控制标准

4 变形控制标准的分级管理方法

为了加强过程控制，建立变形控制标准分级管理机制[20-21]。将每一步开挖下的隧道变形分为Ⅱ级预警、Ⅰ级预警与临界值3个阶段。Ⅱ级预警下可正常施工，需加强监测；Ⅰ级预警下需停止开挖，对支护进行补偿张拉；变形达到临界值时应停止开挖，增加支护措施。大跨过渡段拱顶变形控制标准的分级管理方法见表5。

表5 变形控制标准分级管理

5 现场监测与支护优化

大跨过渡段现场监测点的布置如图6所示。大跨过渡段每5 m设置1个监测断面，选取DK68+280～DK68+460段10个断面进行监测，各个监测断面的最大沉降值见图7。

图6 变形监测点的位置

图7 各监测断面最大沉降值

监测结果表明，大跨过渡段监测到的最大变形为19mm，各个施工步序的变形均小于变形控制标准，表明大跨过渡段支护措施有较大承载冗余，可进行支护措施的降载优化。对大跨过渡段的锚索进行优化如下：取消20 m和26 m跨度的Ⅲ级围岩段锚索，Ⅳ级围岩纵向间距由2.4 m调整到3.6m；32m跨度Ⅲ级围岩锚索纵向间距由4.8 m调整到7.2 m，Ⅳ级围岩纵向间距由2.4 m调整到3.6 m。