基于投资衍生产品的缴费型养老金的最优投资策略

黄 婵, 王 伟*, 温利民

基于投资衍生产品的缴费型养老金的最优投资策略

黄 婵1, 王 伟1*, 温利民2

（1.宁波大学 数学与统计学院, 浙江 宁波 315211; 2.江西师范大学 数学与信息科学学院, 江西 南昌 330022）

研究确定缴费(DC)型养老金可投资衍生产品时的最优投资问题. 假设在金融市场中有3种可投资产品, 包含1种无风险资产、1种股票和1种金融衍生产品. 假定养老金管理者以最大化养老金的期末财富效用为目标, 运用动态随机规划原理, 分别得到了指数效用和幂效用2种情况下DC型养老金最优投资策略的显式解, 给出了风险敞口的数值结果, 并分析了模型参数对风险敞口的影响.

缴费型养老金; 动态规划原理; 最优投资; 衍生产品

由于养老金数额巨大, 养老金投资回报的好坏在很大程度上决定着投保人退休时的养老金水平, 所以关于养老金的资产配置是政府和养老金管理机构非常重视的问题. 1952年, Markowitz[1]发表的“投资组合选择”文章, 标志了现代投资组合理论的创立. 在缴费(Defined Contribution, DC)型养老金最优投资方面, Gao[2]以最大化终值财富的幂效用和指数效用为目标, 利用随机控制理论得到DC型养老金的最优投资策略的解析解. 由于养老金属于长期投资, Zhang等[3]进一步考虑了通货膨胀风险下养老金的最优投资问题. 在国内, 殷俊等[4]考虑了随机利率和通货膨胀风险下养老金的投资组合, 并给出常相对风险规避型(Coefficient of Relative Risk Aversion, CRRA)效用函数下的最优投资策略. 考虑到长寿风险对养老金的重要影响, 王力平等[5]假定了死亡率服从指数分布, 以最大化养老金的期末财富效用为目标, 得到最优投资策略, 并发现死亡率直接影响发放阶段的最优投资比例. 何林等[6]给出了积累期最优投资策略的显式解, 并分析了积累期缴费率、目标替代率、人口老龄化程度等对养老金投资中风险资产配置比例的影响. 岳公正等[7]以股票、基金、国债和1年期银行存款为研究对象, 分析了这4种投资工具的风险、收益及其投资组合, 发现与股市投资相比, 基金投资更有利于分散投资风险. 此外,有实证研究表明[8], 风险资产价格的波动并不是一个常数. 因此, 王远野等[9]进一步考虑了波动率风险, 并假定DC型养老金具有保费返还条款, 研究了均值方差准则下的最优投资问题.

目前, 有关考虑DC型养老金可以用来投资金融市场中衍生产品的研究报道较为鲜见. Zeng等[10]假定养老金管理者不但可以投资金融市场中的股票, 还可以投资衍生产品, 得到了CRRA效用下DC型养老金的稳健最优投资策略. 与文献[10]相比, 本研究考虑了指数效用和幂效用情况下DC型养老金的最优投资问题, 设置幂效用的风险厌恶系数为0与1之间的常数. 利用随机控制理论和分离变量法得到了指数效用和幂效用情况下的最优投资策略的显式解, 并通过数值结果对最优投资策略进行了敏感性分析.

1 金融市场模型

股票的动态价格过程满足如下随机微分方程:

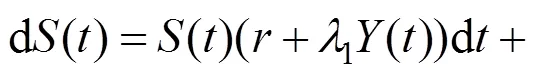
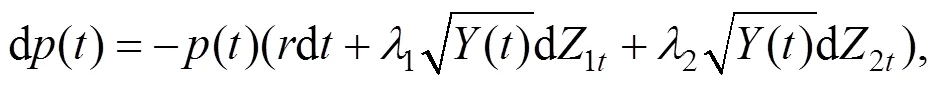
2 财富动态过程

结合式(1)(2)和(5)可得:

其中:

定义上述问题的值函数为:

其中:

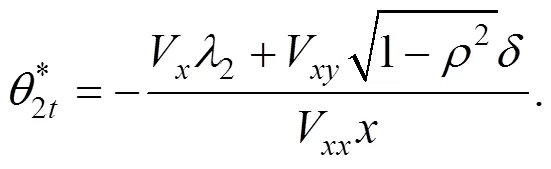
3 最优投资策略

3.1 指数效用函数

对于养老基金管理者, 其目标是使得终端财富的期望效用达到最大, 即

且满足边界条件:

定理1 在指数效用函数下, 最优风险敞口为:

最优值函数为:

(18)

最优投资策略为:

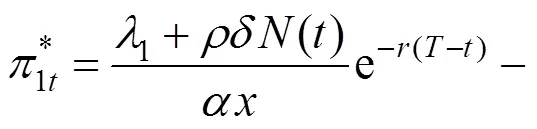
证明 首先猜测方程(14)解的形式为:

将方程(21)~(25)代入HJB方程(14)中, 可得:

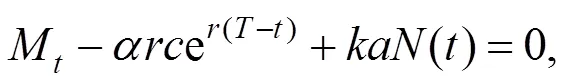
3.2 幂效用函数

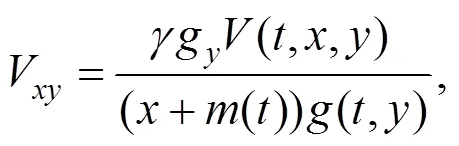
将式(31)~(36)代入方程(14), 则方程(14)可写为:

注意

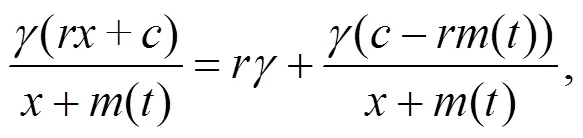
于是有:

则方程(37)满足如下2个方程:

因此, 很容易得到方程(38)的解满足:

电极或者仪表的基本设定参数包括： 温度补偿曲线、电导电池常数，温度偏置等；校准历史包括： 仪表零点校准、斜率校准、验证测量、离线手工取样等操作的执行时间、记录结果等。

其中:

根据Girsanov定理, 可得:

通过Feynman-Kac公式, 方程(42)的解满足:

其中:

此外, 令

其中:

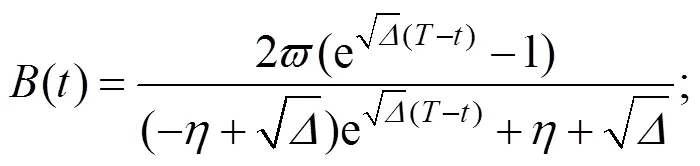
证明 令

则需要满足以下2个方程:

再定义方程(52)的判别式为:

则

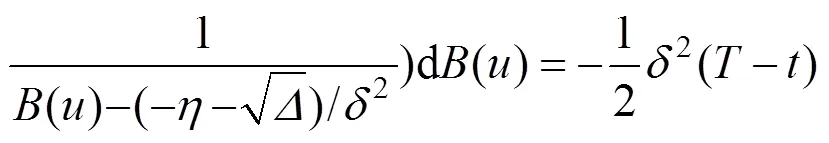
定理2 最优值函数满足:

4 数值算例

图1 指数效用下利率和风险厌恶系数对风险敞口的影响

图2 幂效用下利率和风险厌恶系数对风险敞口的影响

图3 指数和幂效用下缴费率对风险敞口的影响

5 结语

本文主要研究了幂效用和指数效用2种情形下确定缴费型养老金的最优投资问题, 得到了最优投资策略和最优风险敞口的显示解. 研究结果表明: 无论是幂效用还是指数效用, 随着市场利率和风险厌恶系数的增加, 市场风险敞口和波动率风险敞口的绝对值都是减少的; 而随着养老金缴费率的增加, 市场风险敞口和波动率风险敞口的绝对值是增加的. 在后续工作中, 我们将进一步研究含通货膨胀风险和衍生产品情形下确定缴费型养老金的最优投资问题. 此外, 本文中假定利率是常数, 后续将进一步研究当利率满足随机利率的情况.

[1] Markowitz H. Portfolio selection[J]. The Journal of Finance, 1952, 7(1):77-91.

[2] Gao J W. Optimal portfolios for DC pension plans under a CEV model[J]. Insurance: Mathematics and Economics, 2009, 44(3):479-490.

[3] Zhang A H, Ewald C O. Optimal investment for a pension fund under inflation risk[J]. Mathematical Methods of Operations Research, 2010, 71(2):353-369.

[4] 殷俊, 李媛媛. 基于随机利率和通货膨胀的缴费确定型养老金计划最优资产配置策略[J]. 当代经济科学, 2013, 35(2):11-20; 124.

[5] 王力平, 张元萍. 考虑死亡率的DC型养老金资产配置研究的统一框架[J]. 保险研究, 2014(4):121-127.

[6] 何林, 梁宗霞. DC型养老金积累期最优资产配置问题研究[J]. 保险研究, 2016(6):102-111.

[7] 岳公正, 王俊停. 我国社会养老保险基金组合投资风险比较分析[J]. 统计与决策, 2018(8):156-159.

[8] Heston S L. A closed-form solution for options with stochastic volatility with applications to bond and currency options[J]. The Review of Financial Studies, 1993, 6(2):327-343.

[9] 王远野, 樊顺厚, 常浩. 通胀风险与波动风险环境下带有保费返还条款的DC型养老金计划[J]. 系统科学与数学, 2018, 38(4):423-437.

[10] Zeng Y, Li D P, Chen Z, et al. Ambiguity aversion and optimal derivative-based pension investment with stochastic income and volatility[J]. Journal of Economic Dynamics and Control, 2018, 88:70-103.

[11] Liu J, Pan J. Dynamic derivative strategies[J]. Journal of Financial Economics, 2003, 69(3):401-430.

Optimal investment strategies for defined contribution pension with a financial derivative

HUANG Chan1, WANG Wei1*, WEN Limin2

( 1.School of Mathematics and Statistics, Ningbo University, Ningbo 315211, China; 2.School of Mathematics and Information Science, Jiangxi Normal University, Nanchang 330022, China )

The optimal investment problem for DC pension with a financial derivative is studied. We assume that there are three assets in a financial market, including a risk-free asset, a stock and a financial derivative. Assuming that the pension manager aims to maximize the expected utility of the terminal wealth, we use the dynamic stochastic programming principle to obtain the closed-form solutions of the optimal strategies of DC pension fund in both the exponential utility and the power utility. The numerical results of risk exposure and the effect of model parameters on risk exposure are analyzed.

defined contribution fund; dynamic programming principle; optimal investment; derivative

O211.9

A

1001-5132（2020）01-0080-08

2018−11−07.

宁波大学学报（理工版）网址: http://journallg.nbu.edu.cn/

教育部人文社科基金（15YJA910004, 18YJC910012）; 浙江省自然科学基金（LY17G010003）.

黄婵（1994－）, 女, 山西大同人, 在读硕士研究生, 主要研究方向: 金融数学. E-mail: hotop2015@163.com

王伟（1982－）, 男, 安徽安庆人, 博士/副教授, 主要研究方向: 金融数学. E-mail: wangwei2@nbu.edu.cn

（责任编辑 史小丽）