高斯和与有理点的计算

姜 坤,高 伟, 曹 炜

高斯和与有理点的计算

姜 坤,高 伟, 曹 炜*

（宁波大学 数学与统计学院, 浙江 宁波 315211）

有限域; 有理点; 高斯和; 特征

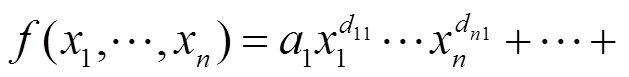
简记为:

其中:

其中:

文献[1]证明了定理1.

定理1[1]设多项式f如式(1)所示, 且

则有:

定理2[2]设多项式f如式(1)所示, 且

并满足:

则

考虑定理2的一般情形, 给出当

1 预备知识

引理1[2]设多项式f如式(1)所示. 令

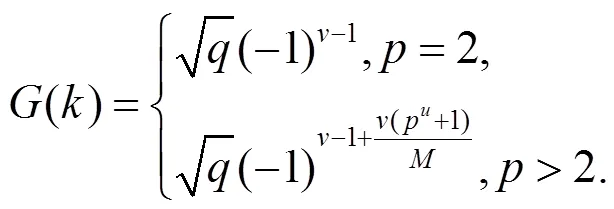
于是由引理2可得引理3.

由二项式定理可得引理4.

2 主要结论

设

定理3 如前所设, 有:

同余方程

同解, 且后者的解均取自

故由引理1和引理3得:

又由引理4可得:

定理得证.

易知:

通过Maple计算, 与该结果一致.

[1] Cao W, Sun Q. On a class of equations with special degrees over finite fields[J]. Acta Arithmetica, 2007, 130(2):195-202.

[2] Wang R Y, Wen B B, Cao W. Degree matrices and enumeration of rational points of some hypersurfaces over finite fields[J]. Journal of Number Theory, 2017, 177:91-99.

[3] Berndt B, Evans R, Williams K. Gauss and Jacobi Sums[M]. New York: Wiley-Interscience, 1998:362-368.

[4] Lidl R, Niederreiter H. Finite Fields[M]. Reading, MA: Addison-Wesley, 1983:186-204.

[5] Cao W, Han S M, Wang R Y. Rational points on Fermat curves over finite fields[EB/OL]. [2019-03-10]. https:// doi.org/10.1142/S0219498817500463.

[6] Zan H X, Cao W. Powers of polynomials and bounds of value sets[J]. Journal of Number Theory, 2014, 143:286- 292.

[7] Zhu M L, Cao W. Invariant factors of degree matrices and L-functions of certain exponential sums[J]. Finite Fields and Their Applications, 2014, 28:188-198.

[8] Pan X L, Zhao X R, Cao W. A problem of Carlitz and its generalizations[J]. Archiv der Mathematik, 2014, 102(4): 337-343.

Gauss sums and computation of rational points

JIANG Kun, GAO Wei, CAO Wei*

( School of Mathematics and Statistics, Ningbo University, Ningbo 315211, China )

finite field; rational point; Gauss sum; character

O156.1

A

1001-5132（2020）01-0065-04

2019−06−22.

宁波大学学报（理工版）网址: http://journallg.nbu.edu.cn/

国家自然科学基金（11871291）;宁波市自然科学基金（2019A610035）.

姜坤（1997－）, 女, 山东梁山人, 在读硕士研究生, 主要研究方向: 数论. E-mail: 718044618@qq.com

曹炜（1974－）, 男, 湖北潜江人, 博士/教授, 主要研究方向: 数论与密码学. E-mail: caowei@nbu.edu.cn

（责任编辑 史小丽）