RNN在降落伞开伞特性研究中的应用

姜添 戈嗣诚,2 李健

RNN在降落伞开伞特性研究中的应用

姜添1戈嗣诚1,2李健1

（1 北京空间机电研究所，北京 100094）（2 中国空间技术研究院航天器无损着陆技术核心专业实验室，北京 100094）

为了对降落伞充气展开过程中的拉力、速度等关键特性进行预测，结合当下机器学习的研究热点，使用循环神经网络对空投试验数据进行学习和训练。文章对原始数据进行了归一化预处理并且采用批量梯度下降的训练方式；试验验证了循环网络方法对充气过程中重要参数进行计算的可行性；并且说明了时间序数索引项在试验中需带入网络参与计算的特点。试验结果表明，使用循环神经网络对训练集数据的开伞速度曲线拟合效果很好；计算结果能够准确反映开伞过程中的拉力变化趋势，峰值误差小于1%，且峰值时刻误差小于2%。

曲线拟合 开伞拉力 循环神经网络 序数索引项 降落伞

0 引言

降落伞作为一种柔性气动减速装置，主要用于飞行器回收、人员救生、空投空降、飞机减速滑跑、武器减速与姿态调整等，在航空航天领域有着广泛的应用。降落伞的典型工作过程一般包括伞系拉直、充气展开、稳定减速三个阶段[1]，其中充气展开过程最为复杂，降落伞在短时间内由拉直状态迅速转变为展开状态，期间经历最恶劣的载荷条件。充气展开过程是降落伞任务期间最重要的工作过程，是可靠性关键环节。充气展开过程的研究内容主要包括降落伞的载荷及应力分布，以及变化历程；伞衣充气形状、阻力面积变化规律等。充气展开过程研究的常用方法主要分为三种：完全试验法[2]、数值模拟法[3]和半理论半试验法[4]。完全试验法通过风动试验、空投试验等物理手段，真实测量给定工况条件下的开伞载荷，成本高、周期长；数值模拟法利用数值计算手段，对开伞充气过程进行流固耦合仿真，受流固耦合技术能力限制，目前不能满足工程设计中对计算简单、快速、准确度相对较高的应用需求；半理论半试验法以同类降落伞的试验数据为基础，以简化的工程计算模型为手段，能够对典型降落伞产品的典型应用工况进行快速、准确的计算分析，是目前工程上最常用的方法，但是该方法具有很大的经验依赖性。

近年来机器学习理论发展迅速，其主要任务是设计和开发可以智能地根据试验数据进行“学习”算法，这些算法可以自动地挖掘隐藏在数据中的模式和规律[5]；人工神经网络[6]则是机器学习领域中最具代表性的一类机器学习方法，是作为一种仿生模型建立起来的计算模型，具有较好的自学习能力和较强的鲁棒性；深度学习则是基于神经网络框架发展出的结构更为复杂、性能更强的神经网络模型[7]，已经在多种学科和不同工程领域中有着广泛的应用。相比传统方法，深度学习具有不依赖高品质特征的优势[8]，所谓高品质特征这里可以简单理解为基于物理方程的研究方法，即深度学习可以通过直接训练试验数据来反映输入与输出之间的关系，以减少由假设与简化带来的对计算结果的影响。

典型的深度学习模型有全连接神经网络[9]（DNN）、深度置信网络[10]（DBN）、卷积神经网络[11]（CNN）、循环神经网络[12]（RNN）等，每种方法均有各自的特点。DNN是起步最早、应用最广的模型，但是训练效率较低且易受到初始参数的影响；DBN则是2006年由Hinton针对上述问题提出的改进模型，可以有效提升模型的建模和推广能力；CNN目前在图像处理与模式识别中的应用极为火热，能够对图像中的高层次信息进行处理；RNN是专门用于处理序列数据的模型，能够储存和传递多个时刻前的序列信息，主要应用于自然语言处理（NLP）、语音识别、机器翻译等方面。

虽然循环网络在NLP等方面表现出了得天独厚的优势与强大的使用效果，目前已经被应用于互联网行业等相关领域当中，但是循环网络甚至整个机器学习领域与绝大部分传统工业的交叉融合使用仍处于初步探索的阶段，如可靠性中故障时间预测[13]、石油勘探中井测曲线生成[14]等。但是在降落伞相关行业中，国内外可参考的文献仅限于部分使用全连接网络对伞稠透气性[15]和伞衣织物强度[16]进行研究，开伞特性方面的相关研究更是少之又少。文献[17]将全连接网络与数值模拟进行混合应用，该方法结合试验数据用于补偿开伞过程中载荷传感器的应力值，可明显减小网络规模与缩短建模周期，但是尚未有可参考的使用循环网络对开伞特性进行研究的相关文献。该网络模型与降落伞的交叉应用仍具有极大的挖掘空间。

本文首先介绍了RNN模型的结构和基于时间的反向传播算法的原理，并在试验结果中说明了RNN在空投数据的应用中需要将时间序数索引项作为输入特征参与神经网络计算的特点，最后给出了RNN模型在三组试验数据中对拉力和三向速度的拟合情况，验证了循环神经网络在开伞特性预测中具有较好的表现能力。

1 原理与方法

人工神经网络是机器学习理论中的一个重要分支，云计算、大数据时代使得神经网络领域逐渐在模式识别、图像处理、语音识别、金融预测等复杂问题方面表现出一定的优势。神经网络中最基本的成分是神经元模型[18]。神经元接收到来自其他神经元传递过来的输入信号，这些输入信号通过带权重的连接进行传递，神经元接受到的总输入值将与神经元的阈值进行比较，然后通过激活函数处理后产生神经元的输出。

神经网络的组成结构一般分为输入层、隐藏层和输出层三部分，反映了一种由输入到输出的映射关系，一般来说，神经网络的模型复杂度越高、参数容量越大，对复杂函数逼近的能力就越强。

1.1 循环神经网络

循环神经网络是一种非常强大的深度学习模型，是一类专门用于处理序列数据的神经网络，近年来在计算机行业中发展十分迅速，也常被用于金融行业的股市、房价预测，同时在水利[19]、地质[20]等大型工程领域中也有一定的研究和应用。

循环网络是在全连接网络的基础上发展而来，同样由输入层、隐藏层和输出层组成，如图1所示。它不仅能够实现信息由输入至输出逐层传递的经典结构，而且RNN的隐藏层神经元之间还存在着信息的互联互通，因此它可以用于处理语言、文字等具有明显前后关系的序列案例。由于RNN具有在神经元间横向传递信息的能力，能够在一定程度上表达数据之间的相关性，这种信息的传递与空投试验中真实的物理过程十分匹配——前一时刻的速度、拉力等物理量会直接对下一时刻的飞行状态产生影响，因此本文选用RNN来预测开伞过程中的开伞拉力、前体运动速度等重要物理特性。

图1 RNN模型计算

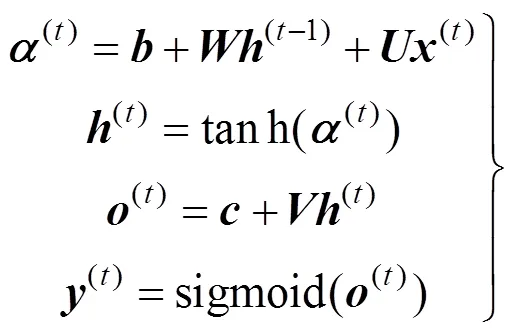
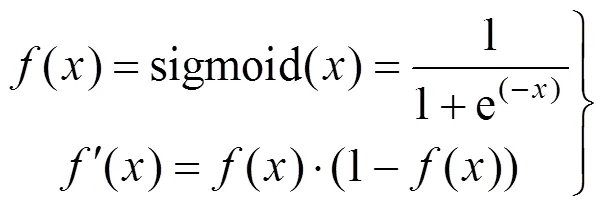
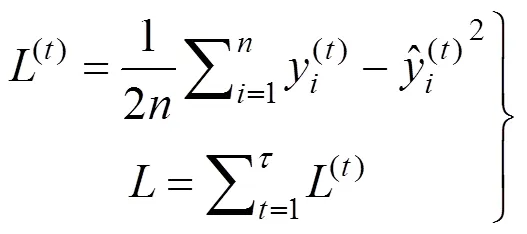
1.2 基于时间的反向传播算法

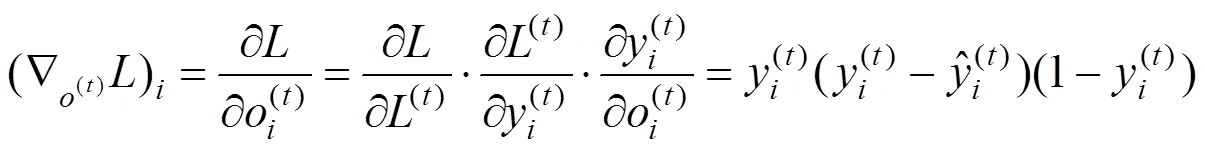
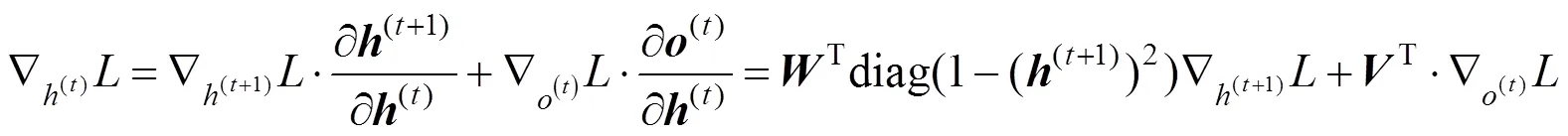
4）根据式（4）、（5）、（6）可获得计算图内部所有节点的梯度，并根据链式法则获得参数，，，，关于时间的梯度变化，其总梯度为各时刻的梯度和

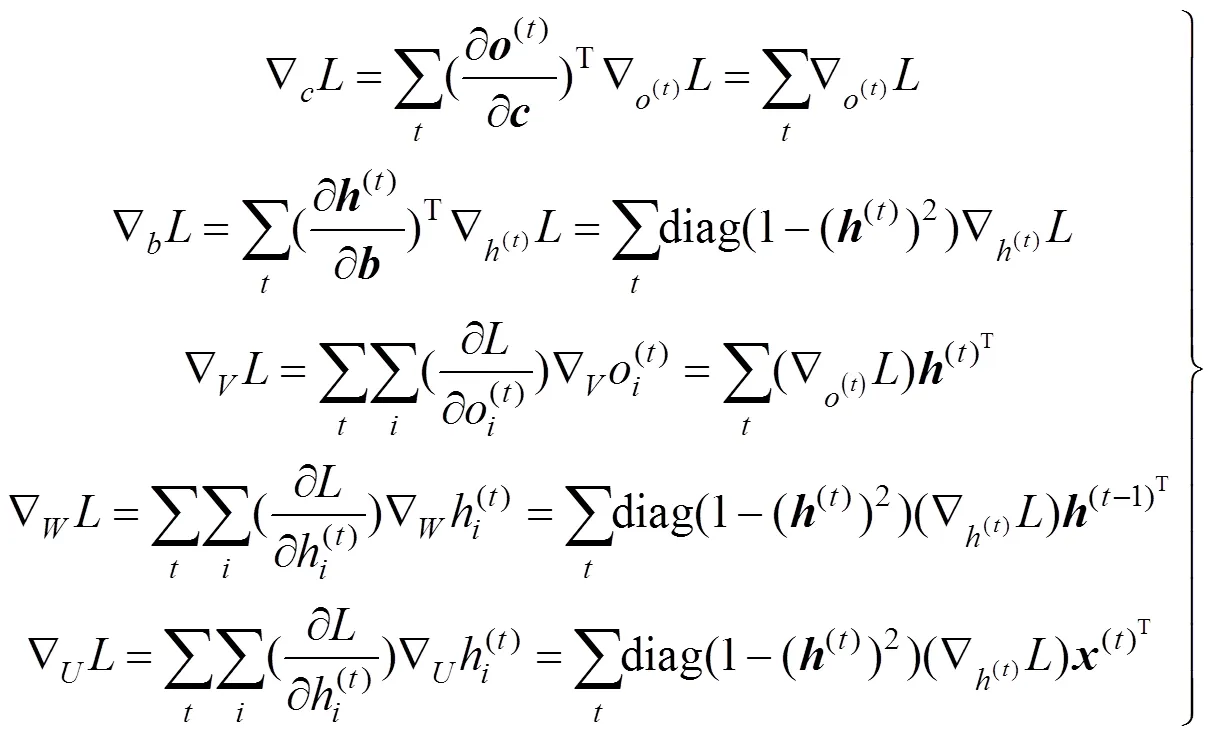
其余权重参数的更新方法与式（8）相同，这里不再赘述。

2 试验验证与结果分析

2.1 指标选取与数据处理

试验数据来自于相同条件下的三次低空开伞空投试验：对配质量为6 040 kg的箭头模型进行盘缝带伞开伞载荷测试试验，伞名义面积为200 m2，开伞方式为无限质量开伞。试验过程中的传感器主要为伞拉力传感器与GPS接收机，拉力传感器包括时间与拉力信号，采样频率为2 kHz，GPS信号包括时间、高度、东向速度、北向速度、天向速度、经纬度信息；气象信息使用当地月平均气象参数统计值或者空投试验前的实测值，包括不同高度的温度、湿度、密度、气压、风速、风向。总结各传感器及其他信息的数据特征如表1所示。

表1 数据特征种类表

Tab.1 Varieties of data characteristic

由于拉力传感器、GPS传感器和探空气球的采样频率不同，首先对数据进行处理，使各数据以时间对齐，获得开伞过程中同一时刻下的拉力、北向速度、东向速度、天向速度、高度、温度、密度和气压，其中拉力与三向速度作为输出，高度、气象数据与时间信息作为输入。

经过归一化的数据可以加快梯度下降的求解速度，并且可以使不同的特征具有相同的尺度，本文的归一化方法采用min-max标准化方法，归一化范围根据空投试验的真实情况决定，既要保留一定的余量也要使经过归一化的数据尽量在（0,1）区间内均匀分布，具体范围如表2所示，以此表所列数据特征作为本文试验的标准输入，其中速度项负值表示速度方向。

表2 归一化范围表

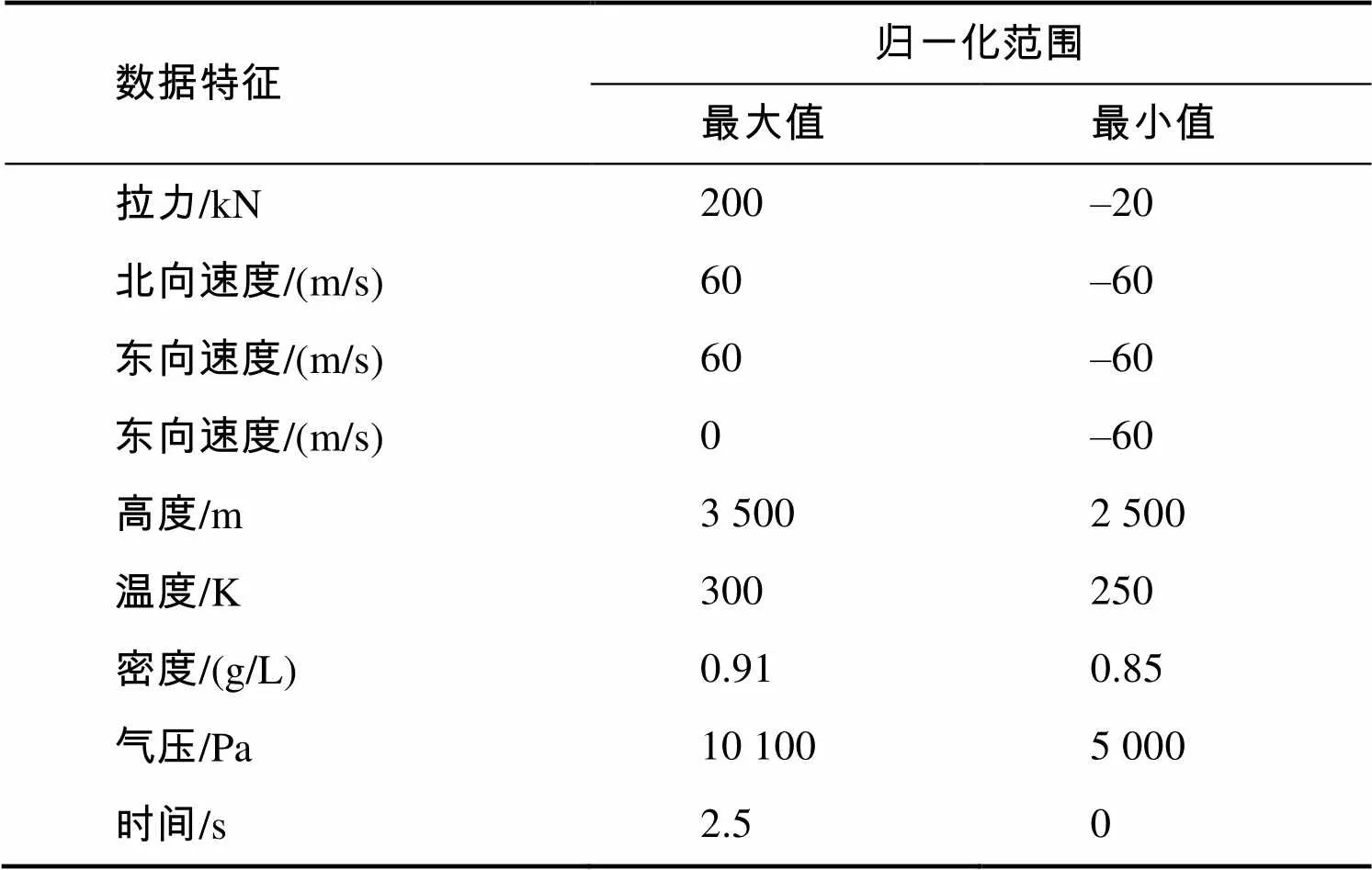
Tab.2 Range of characteristic normalization

图2 样本训练方式示意

2.2 结果分析

在RNN应用最为广泛的领域，如文字、音频、图像等，并没有将索引项作为输入特征参与计算的案例。而在本试验中，时间是样本数据的序数索引，但是从图3不同输入特征对试验结果的影响中可以明显看出，如果输入特征中不包含时间项，通过式（3）计算出的均方误差很难收敛，即使能够收敛，开伞拉力的拟合曲线也不准确；将时间项不仅看作序数索引，而且作为输入特征带入神经网络参与计算后，训练结果产生了质的飞越，均方误差不仅能够较快收敛至极小的数值，而且试验结果能与拉力传感器的真实数据较好匹配。从上述试验可得，RNN的传统使用方法中对序数索引项的应用方式与本试验有所不同，该不同点在研究初期确实对试验过程造成了非常大的困扰，但是经过多次探索、改进和试验验证后，本文采用的网络输入方式能够证明循环神经网络模型在开伞特性拟合中的适用性。

图3 不同输入特征对试验结果的影响

通过上述试验确定RNN在本试验中的应用特点后，对所有试验数据进行训练，经过多次迭代，训练样本的均方误差逐渐收敛，保存稳定后的各参数值，，，，；新的输入利用上述参数使用前向传播公式计算输出结果。由于本试验中暂没有新数据用于验证，所以只能使用训练集的三次空投试验数据测试结果精度。输出特征使用的是拉力和各项速度，并计算了空投试验中较为关注的最大开伞拉力大小与峰值时刻，各试验中的三向速度与拉力曲线如图4所示。

图4 输出特征结果比较

图4（a）、（b）、（c）中三次空投试验不同速度的拟合结果均与各试验的曲线较为匹配，三次空投试验的三速变化曲线不同，试验结果均能较为准确地反映出符合该试验的速度变化情况。从图4（d）的拉力曲线中可以看出，训练结果拉力的增长趋势与真值曲线非常吻合，开伞的峰值拉力与拉力峰值时刻比对表如表3所示。此训练样本中的拉力峰值误差均在1%以内，峰值时刻误差在2%以内；另一方面，从三次空投试验的传感器数据中可以看出，低空开伞下，盘缝带从拉直到拉力峰值的过程中会有出现一个拉力波动点，该波动点出现的原因是盘缝带伞在充气张满的过程中会出现一种“四叶花瓣”的状态，伞衣从“四叶花瓣”状态到展开圆形的过程中，伞衣出现外翻时，反映在拉力曲线上就会出现短暂的卸载区，试验的拟合结果中也准确表现出了该卸载状态和时间，但是在试验一与试验二的峰值点附近也出现了类似的卸载状态，训练结果中未能表现出该拉力特点。

表3 峰值拉力与峰值时刻比对表

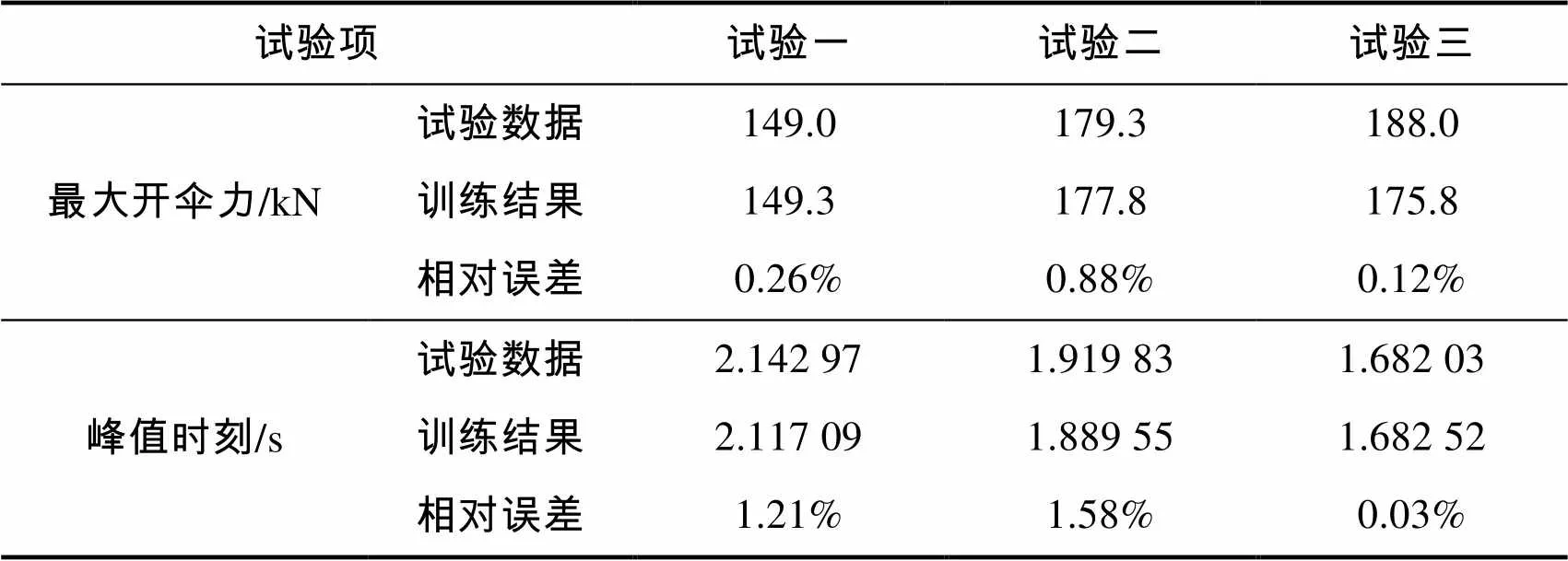
Tab.3 Peak force & time of simulation & experiment data

3 结束语

使用RNN对降落伞开伞过程中部分重要特性进行回归分析后，可以得出以下结论：

1）RNN能够在开伞特性预测中表现出较好的试验结果，验证了利用RNN方法对降落伞充气过程计算的可行性。

2）时间项在本试验中不仅需要最为序数索引项参与样本数据的排列，还必须作为一项输入特征带入神经网络计算。

3）RNN训练的结果在速度和拉力的拟合中表现优秀，能够准确的反映出速度和拉力的变化趋势，对训练集的复现十分准确，多次试验的峰值拉力误差均在1%以内，峰值时刻误差在2%以内。

References)

[1] 黄伟. 降落伞最小弹射分离速度的计算方法[J]. 航天返回与遥感, 2018, 39(2): 26-33.HUANG Wei. The Calculation Method of Minimum Ejection Velocity of the First Stage Parachute[J]. Spacecraft Recovery & Remote Sensing, 2018, 39(2): 26-33. (in Chinese)

[2] WIDDEL H, ROSE G, BORCHERS R. Results of Conductivity, Ion Mobility and Ion Concentration Measurements Taken with a Parachute Gerdien Condenser Experiment During the Winter Anomaly Campaign[J]. Space Research, 1978, 11(8): 125-127.

[3] ZHU Y, LIU L, WANG Z P. Flow Field Characteristics for Parachute-projectile System[J]. Chinese Journal of Mechanical Engineering, 2011, 24(5): 813-819.

[4] 王海涛, 秦子增. 基于遗传算法的大型降落伞气动力参数辨识[J]. 国防科技大学学报, 2010, 32(1): 28-33 WANG Haitao, QIN Zizeng. Aerodynamic Parameter Estimation of Large Parachute Based on Genetic Algorithm[J]. Journal of National University of Defense Technology, 2010, 32(1): 28-33. (in Chinese)

[5] 孙志远, 鲁成祥, 史忠植, 等. 深度学习研究与进展[J]. 计算机科学, 2016, 43(2): 1-8. SUN Zhiyuan, LU Chengxiang, SHI Zhizhong, et al. Research and Advances on Deep Learning[J]. Computer Science, 2016, 43(2): 1-8. (in Chinese)

[6] HALBERT W. Learning in Artificial Neural Networks: A Statistical Perspective[J]. Neural Computation, 2014, 1(4): 425-464.

[7] BENGIO Y, LAMBLIN P, POPOVICI D, et al. Greedy Layer-wise Training of Deep Networks [C]// Advances in Neural Information Processing Systems 19. Cambridge: MIT Press, 2007: 153-160.

[8] LECUN Y, BENGIO Y, HINTON C. Deep Learning[J]. Nature, 2015, 521(7553): 436-444.

[9] HINTON G, LI D, DONG Y, et al. Deep Neural Networks for Acoustic Modeling in Speech Recognition: The Shared Views of Four Research Groups[J]. IEEE Signal Processing Magazine, 2012, 29(6): 82-97.

[10] HINTON G, OSINDERO S, TEH Y. A Fast Learning Algorithm for Deep Belief Nets[J]. Neural Computation, 2006, 18(7): 1527-1554.

[11] BOUVRIE J. Notes on Convolutional Neural Networks[D]. Cambridge: MIT, 2006.

[12] SAON G, PICHENY M. Recent Advances in Conversational Speech Recognition Using Convolutional and Recurrent Neural Networks[J]. IBM Journal of Research and Development, 2017, 61(4): 1: 1-1: 10.

[13] 王鑫, 吴际, 刘超, 等. 基于LSTM循环神经网络的故障时间序列预测[J]. 北京航空航天大学学报, 2018(4): 772-784.WANG Xin, WU Ji, LIU Chao, et al. Exploring LSTM Based Recurrent Neural Network for Failure Time Series Prediction[J]. Journal of Beijing University of Aeronautics and Astronautics, 2018(4): 772-784. (in Chinese)

[14] URSULA I, JORGE O. Artificial Neural Networks Applied to Estimate Permeability, Porosity and Intrinsic Attenuation Using Seismic Attributes and Well-log Data[J]. Journal of Applied Geophysics, 2014(104): 45-54.

[15] 赵敏, 许家骅, 肖冲. BP神经网络预测降落伞绸透气性的研究[J]. 产业用纺织品, 2008, 26(8): 22-25. ZHAO Min, XU Jiahua, XIAO Chong. A Study of Prediction of Air Permeability of the Parachute Fabric by BP Neural Network[J]. Technical Textiles, 2008, 26(8): 22-25. (in Chinese)

[16] LEVENT O, MITHAT Z, MAHMUT K, et al. Predicting the Seam Strength of Notched Webbings for Parachute Assemblies Using the Taguchi’s Design of Experiment and Artificial Neural Networks [J]. Textile Research Journal, 2009, 79(5): 468-478.

[17] 罗韬, 庄毅. 基于神经网络杂交模型的降落伞动态应力补偿方法[J]. 航天返回与遥感, 2015, 36(5): 20-28. LUO Tao, ZHUANG Yi. Research of Dynamic Stress-compensation Method for Parachute Based on Neural Network Hybrid Model[J]. Spacecraft Recovery & Remote Sensing，2015, 36(5): 20-28. (in Chinese)

[18] HUBEL D, WIESEL T. Receptive Fields Binocular Interaction and Functional Architecture in the Cat’s Visual Cortex[J]. The Journal of Physiology, 1962, 160(1): 106-154.

[19] 梁肖, 李端超, 黄少雄, 等. 基于递归神经网络的火电机组污染物排放研究[J]. 自动化与仪表, 2017, 32(10): 72-75. LIANG Xiao, LI Ruichao, HUANG Shaoxiong, et al. Research on Quantity of Power Unit Pollutant Emission Based on Recurrent Neural Networks[J]. Automation & Instrumentation, 2017, 32(10): 72-75. (in Chinese)

[20] 张东晓, 陈云天, 孟晋. 基于循环神经网络的测井曲线生成方法[J]. 石油勘探与开发, 2018, 45(4): 629-639. ZHANG Dongxiao, CHEN Yuntian, MENG Jin. Synthetic Well Logs Generation Via Recurrent Neural Networks[J]. Petroleum Exploration and Development, 2018, 45(4): 629-639. (in Chinese)

[21] RUMELHART D, HINTON G, WILLIAMS R. Learning Representations by Back Propagating Errors[J]. Nature, 1986, 323(6088): 533-536.

[22] PINEDA F. Generalization of Back-propagation to Recurrent Neural Networks[J]. Physical Review Letters, 1987, 59(19): 2229-2232.

Application of RNN in the Study of Parachute Opening Characteristics

JIANG Tian1GE Sicheng1,2LI Jian1

（1 Beijing Institute of Space Mechanics & Electricity, Beijing 100094, China）（2 Key Laboratory for Nondestructive Spacecraft Landing Technology of CAST, Beijing 100094, China）

To predict the essential characteristics such as strain of suspension-line and velocity of descent in the parachute deployment process, this paper uses recurrent neural networks to train the airdrop experiment data through the combination of machine learning and parachute research method. The normalization of original data and batch gradient descent is applied to verify the feasibility of RNN to calculate the important parameters in the inflation process. The research result gives the explanation of the input characteristic about the time series index items that need to participate in the calculation of the networks. Meanwhile, the conclusion shows that the method of using the RNN is appropriate to the curve fitting of the velocity of descent. The calculation results can accurately reflect the trend of the suspension-line strain in the parachute deployment process, the peak error is less than 1% and the peak time error is below 2%.

curve fitting; deployment tension; recurrent neural networks; series index; parachute

TP753

A

1009-8518(2019)06-0035-09

10.3969/j.issn.1009-8518.2019.06.005

姜添，男，1994年生，2017年获北京航空航天大学工程力学专业学士学位，现在中国空间技术研究院飞行器设计专业攻读硕士学位，研究方向为回收着陆技术。E-mail：jetinjiang@foxmail.com。

2019-08-10

姜添, 戈嗣诚, 李健. RNN在降落伞开伞特性研究中的应用[J]. 航天返回与遥感, 2019, 40(6): 35-43.

JIANG Tian, GE Sicheng, LI Jian. Application of RNN in the Study of Parachute Opening Characteristics[J]. Spacecraft Recovery & Remote Sensing, 2019, 40(6): 35-43. (in Chinese)

（编辑：王丽霞）