3-呋喃甲酸红外光谱及分子间相互作用的理论研究

李会学，王家朋

甘肃省新型分子材料设计与功能重点实验室，天水师范学院化学工程与技术学院，甘肃 天水 741001

引 言

作为重要原料的呋喃甲酸，在制药工业及化学工业中可用来合成糠酰胺、甲基呋喃、糠酸酯及其盐等产品[1]。由于该有机酸用途广泛，其各种物理、化学及生物性能得到了深入研究，最新研究发现2-呋喃甲酸分子中的C—H单键经羧基化再质子化可制备2,5-呋喃二甲酸，该方法可利用大量生物质作为原料，进一步合成生物基塑料—聚乙烯呋喃二甲酸乙二醇酯[2]。另外呋喃甲酸经Diels-Alder环加成芳构化反应，可合成多种高效、广谱杂环抗菌剂及稀土类呋喃羧酸配合物，该类配合物具有优异的发光性能，可拓宽呋喃甲酸在药物、材料领域的用途[3-5]。Özcan等发现当在纳米管Ti/TiO2上负载Pt作催化剂，在水溶液中经光催化可选择性地将糠醛氧化为5-甲酰-2-呋喃甲酸[6]。Nadykto等采用密度泛函理论计算了呋喃甲酸衍生物(2-Methyl-5-[(1S,2S,3R)-1,2,3,4-tetrahydroxybutyl]-3-furoic acid)与大气中硝酸根、硫酸根等阴离子的相互作用，发现这些物种能强烈键连形成团簇，并具有很高的稳定性，人工降雨中成核效果明显[7]。然而关于呋喃甲酸的分子间作用力理论研究，特别是其对分子振动及红外光谱的影响研究未见报道，分子的振动模与化学反应机理、分子的电子振动耦合光谱以及红外、拉曼光谱等具有直接或间接的关系，当分子的振动模式受到干扰时振动频率及强度将会改变，还可能产生各种泛频。本工作根据密度泛函理论(density functional theory, DFT)和二级微扰理论(secondorder møller-plesset，MP2)，对3-呋喃甲酸分子的单体和二聚体进行理论计算，通过与实验数据对比，探讨分子间作用力对分子振动频率的影响，为呋喃甲酸的应用提供理论支撑。

DFT与MP2方法都考虑了电子相关作用，能较好地预测分子的物理、化学性质，是广泛使用的电子结构理论[8-9]，对3-呋喃甲酸进行模拟计算时，为体现羧基的强极性，选用了三重分裂、包含极化项及弥散项的6-311+G(d, p)基组。基于优化的分子构型，计算了3-呋喃甲酸的红外光谱，结合Gaussian View程序对振动频率进行了指认。另外，为考察分子间相互作用对分子振动频率的影响，从单晶晶胞中选取了距离最近的二聚体分子进行优化，考察分子间相互作用能时考虑了基组叠加误差(BSSE)和零点能(ZPE)校正，并运用自然键轨道分析(NBO)探究了分子间作用力的本质。所有操作均由Gaussian 09软件包完成，计算的收敛精度由程序默认设置提供。

1 单分子构型及其红外光谱

1.1 单分子几何构型

3-呋喃甲酸的晶胞中包含4个分子，该晶胞属于单斜晶系的P21/c空间群[10]，三条晶轴a，b，c的长度分别为5.189，8.886和16.223 nm，晶轴夹角α，β，γ分别为90°，91.06°以及90°，沿着a轴(附图1中的OA方向)两个相邻晶胞结合在一起，从附图1可以看出，左边晶胞的第二个呋喃甲酸分子与右边晶胞的第三个呋喃甲酸分子处在同一平面上，这两个处在不同晶胞的相邻分子通过羰基接触紧密，以氢键形式结合在一起，形成较强的分子间作用力。

从该晶体中取出单个分子作为输入文件，经B3LYP及MP2方法优化后的几何构型如图1构型Ⅰ所示，所得分子的结构参数列在附表1中，与实验数据比较，各种计算的键参数吻合得较好，B3LYP计算所得键长偏差最大为0.015 nm，键角偏差最大为8.22°，MP2方法得到的键长、键角最大偏差分别为0.016 nm和8.19°，两种方法得到的二面角最大偏差都为6.70°，并且都为∠O10—C9—O11—H12，表明两种理论对于该分子的构型优化是合理的。

另外考虑到呋喃甲酸分子的呋喃环可以形成共轭π—键，稳定构型中呋喃甲酸的原子将是共平面的，但羧基与之相连的C—C键相对可以自由转动，因此保持共平面的呋喃环不动，绕化学键C3—C9转动羧基，当旋转180°时得到了另一个稳定构型并对其进行优化，如图1构型Ⅱ所示，与构型Ⅰ相比，二面角(C2—C3—C9—O10)从-0.001°变为-179.996°。如果将构型Ⅰ作为标准，即设其相对能量为0 kJ·mol-1，则构型Ⅱ相对能量为0.99 kJ·mol-1，构型Ⅰ比构型Ⅱ能量稍小一些，根据玻尔兹曼统计分布公式，室温下(300 K)前者占97.1%，后者只占2.9%，构型Ⅰ向构型Ⅱ转化属于异构化反应，必须克服一定的势垒才能完成，对该反应的过渡态进行理论计算，存在唯一虚频-91.48 cm-1，经内禀反应坐标分析，过渡态沿反应坐标方向分别指向构型Ⅰ和构型Ⅱ，证实该过渡态是所要求的正确构型(图1中最右边结构)。另外图2对异构化反应的能级进行了分析，从图可以看出反应能垒为32.10 kJ·mol-1，由于该势垒相对较大[11-12]，常温下构型Ⅰ很难转化为构型Ⅱ。上述波兹曼统计分析以及过渡态理论计算都表明构型Ⅰ是实际存在的稳定结构，单晶中没有构型Ⅱ，因此所有计算均基于构型Ⅰ。

图1 3-呋喃甲酸构型Ⅰ，Ⅱ及其过渡态结构

图2 3-呋喃甲酸异构化反应中的能量变化图

1.2 单分子红外光谱及归属

基于优化后的分子构型Ⅰ, 在B3LYP/6-311+G(d, p)水平下对3-呋喃甲酸的振动光谱进行了计算。根据谐振势模型，简正振动模可以通过力常数矩阵、本征向量矩阵及简正振动坐标乘积联系起来，这种方法使得振动模在数学上处理起来较为方便，但不能直接与通常直观的伸缩、变形振动联系起来，但Gaussian程序利用freq=internal命令能将分子的振动模式投影到各冗余内坐标上，并可计算出每个冗余内坐标所分配的势能占该振动模势能的百分比，即势能分布(potential energy distribution, PED)，利用Gauss View程序的三维动画可方便地对某一振动模式进行伸缩、变形等振动的具体指认[13]，可直观地分析该振动的特征。

由于呋喃甲酸分子中含有12个原子，共30种简正振动模式，当分子为完全平面构型的情况下，分子具有Cs对称性，根据群表示理论可将振动模式归属于21个A′不可约表示及9个A″不可约表示，但由于实际分子呋喃环与羧基二面角为2.62°，不是完全平面的，不具有Cs对称性，故本文不做对称性分析。我们首先对全部振动能量进行二阶导数分析，得到谐振势模型下的谐性频率，在此基础上植入非谐性项，即通过微分得出三阶力常数和半对角四阶力常数，计算出非谐振子的振动频率[14]，经计算该分子的谐性频率及非谐性频率分布范围为3 626～68 cm-1, 计算得到的分子红外光谱如图3所示, 表1列出了部分计算的谐性频率、非谐性频率及实验频率数值、势能分布及振动归属, 所有的计算结果在辅助材料中附表3中给出。

表1B3LYP/6-311+G(d, p)，MP2/6-311+G(d, p)计算得到的3-呋喃甲酸部分振动的红外强度(IRint/km·mol-1)、频率(cm-1)和势能分布(%)

Table1ThecalculatedIRintensity(IRint/km·mol-1),frequencies(incm-1)andPED(%)ofthepartvibrationsin3-furoicacidatB3LYP/6-311+G(d,p)andMP2/6-311+G(d,p)

FrequenciesExp.MP2B3LYPHarmAnharmIRintPED/%Assignationν1540571.86591.88511.8816.73D(3, 9, 11, 12)(9.3), D(10, 9, 11, 12)(11.6)furan ring and hydroxywagging out-planeν2691720.79747.00682.0476.63D(2, 3, 4, 8)(11.8), D(2, 3, 9, 10)(12.4), D(10, 9, 11, 12)(12.8)carboxyl wagging out-planeν3765760.59810.15760.5712.19D(2, 3, 4, 8)(13.7), D(9, 3, 4, 8)(19.4), D(8, 4, 5, 1)(10.7)furan ring and carboxyl torsion out-planeν41 1181 099.521 133.681 093.62127.91R(1, 5)(11.4), R(4, 5)(14.0), A(1, 2, 7)(12.0)furan ring deformationν51 1661 161.331 195.731 143.5113.12A(3, 4, 8)(16.7), A(5, 4, 8)(16.9), A(9, 11, 12)(13.5)H of furan rocking + hydroxyl rockingν61 5931 587.491 540.761 565.8329.97R(3, 4)(12.6), A(3, 2, 7)(10.4)furan ring stretchν71 7701 723.841 724.421 761.40463.90R(3, 9)(13.3), R(9, 10)(24.2), A(3, 9, 11)(10.3), A(9, 11, 12)(12.3)COstretch+CCstretch+hydroxy scissoringν83 5893 620.793 626.003 583.1795.08R(11, 12)(93.2)hydroxyl stretch

Harm: 谐性频率, AnHarm: 非谐性频率, D: 二面角, A: 键角, R: 键长,ν1振动D(3, 9, 11, 12)(9.3)表示由C3，C9，O11，H12四个原子组成的二面角扭转振动势能占总能量的9.3%, 其余类推

Ham: Harmonic frequency; Anham: Anharmonic frequency; D: Dihedral angle; A: Bond angle; R: Bond length;ν1vibration mode D(3,9,11, 12)(9.3) expresses the torsional potential energy of dihedral angle composed of C3, C9, O11, H12four atoms that is 9.3% of total energy, and so on.

图3 B3LYP/6-311+G(d, p)计算得到的红外光谱(a)及局部放大的图(b)

Fig.3ThecalculatedIRspectrumatB3LYP/6-311+G(d,p) (a)andthepartialenlarged(b)

图4 3-呋喃甲酸气相实验红外光谱(引自http://202.127.145.134/scdb/)

2 二聚体分子构型及其红外光谱

2.1 二聚体分子间相互作用

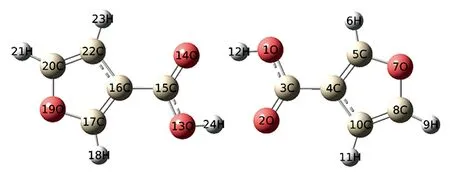
图5 单晶中及MP2优化后二聚体

2.2 二聚体分子间相互作用NBO分析

计算二聚体的结合能时避免不了基组重叠误差, 可通过完全均衡校正(counterpoise procedure)方法消除之[18], 通过上述方法得到的二聚体的结合能为-130.55 kJ·mol-1, 即每个氢键提供65.27 kJ·mol-1的结合能，该值远大于一般的分子间作用力，表明两分子之间存在较强的相互作用，不管是单晶还是计算优化得到的二聚体分子都保持中心对称，氢键使得二聚体能量降低, 构型更稳定, 可以预计将3-呋喃甲酸做压片处理, 主要是以这样的二聚体存在。为了进一步探讨其相互作用的本质, 我们通过二级微扰理论分析了给体—受体轨道的相互作用[19], 获得了电荷转移及二级稳定化能等参数(数据见表3), 二阶稳定化能与轨道间的作用力成正相关，二阶稳定化能越大, 则供体给体轨道相互作用越强, 供体轨道向受体轨道提供的电子越多。由表3可知, 二聚体中两个强氢键, 即O1—H12…O14和O2…H24—O13, 以O2…H24—O13为例, O2提供两对孤对电子, 与反键轨道BD*[H24—O13]作用, 分别形成35.4及86.0 kJ·mol-1的二级稳定化能, 故该氢键的总的二级稳定化能为121.4 kJ·mol-1, 在形成二聚体的过程中, 羰基上O2的孤对电子向反键BD*[O13—H24]轨道转移0.067个电子电量, 并且这些电荷在反键BD*[H24—O13]主要分布在H24上(占比为77.88%), 分布在O13原子上的只占22.12%, 同样氢键O1—H12…O14 的电子转移及二级稳定化能也完全相同。经自然键轨道分析单体中羰基O2的孤对电子所占据轨道的杂化状态为sp99.99杂化型的轨道, 该轨道几乎全由2p轨道组成, 形成二聚体后, 相同轨道杂化类型变成了sp30.15, 很明显2p轨道成分减小, 而2s轨道成分增加, 加强了给体与受体轨道的有效重叠(图6), 轨道间的相互作用增大。由此可见, 该二聚体的分子间氢键主要来自于羰基氧原子的孤对电子与相邻分子羧基上羟基的反键轨道的相互作用。

表2 二聚体中的键参数

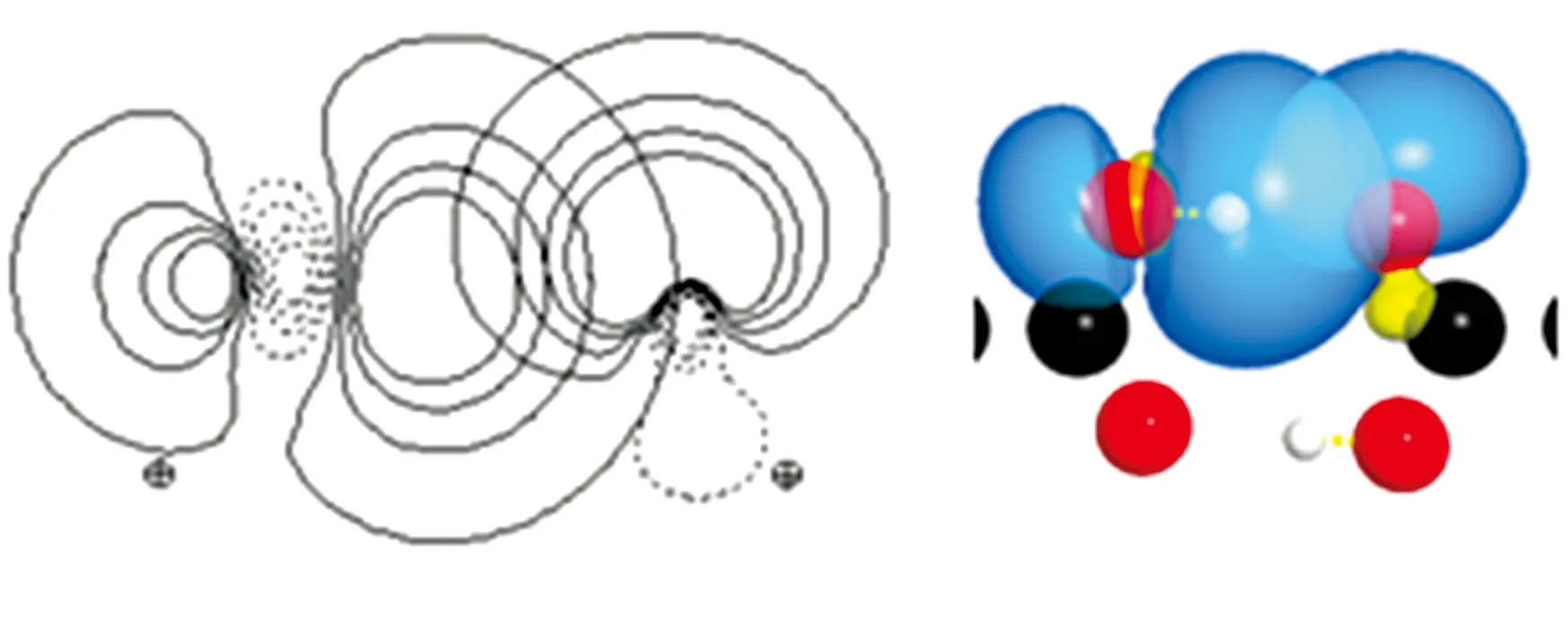
图6 LP[O2]给体轨道与BD*[O13—H24]受体轨道的二维(a)及三维(b)重叠示意图

Fig.6StereogramandplanargraphofthedonororbitalLP[O2]andacceptororbitalBD*[O13—H24]

表33-呋喃甲酸二聚体电荷转移(CT)、给体受体轨道以及二阶稳定化能

Table3Thechargetransfer，donorandacceptororbital(Фi, Фj)andsecondorderstabilizationenergy(ΔE2)

CT(e)Фi→ФjΔE2/(kJ·mol-1)0.067LP(1)O2→BD*(1)O13—H2435.42LP(2)O2→BD*(1)O13—H2486.000.067LP(1)O14→BD*(1)O1—H1235.45LP(2)O14→BD*(1)O1—H1285.95

Фi： 给体轨道, Фj： 受体轨道

Φi: Donor orbit;Φj: Acceptor orbit

另外我们还计算了压强为1 atm, 不同温度下二聚体的自由能变, 所得结果列在附表4中。温度为300 K, 压强为1 atm时, 3-呋喃甲酸分子形成二聚体时, Gibbs自由能变为-14.35 kJ·mol-1, 从热力学第二定律可知, 两个呋喃甲酸分子可自发生成二聚体。当温度升高到500 K时, Gibbs自由能由负变正, 说明该条件下, 二聚体将自发分解为两个呋喃甲酸分子, 这从热力学角度给出了常温(300 K)下呋喃甲酸通过分子间作用力形成二聚体是有利的。另外根据公式ΔG=ΔH-TΔS, ΔG与ΔH成正相关, 而与TΔS成负相关, 由于反应物是两个单分子, 反应后产物为一个二聚体分子, 混乱度减小, 故不同温度下熵变ΔS基本保持不变且为负值, 温度升高有利于ΔG的增加, 从表中可以看出, 焓变随温度升高而增大, 因此温度越高ΔG越正, 越不利于二聚体的稳定。

2.3 二聚体氢键对红外光谱的影响

呋喃甲酸的晶体结构表明晶胞中分子都是平行排列的，每个分子都被其他分子所包围，不可避免要受到分子间作用力影响，当样品经研磨与KBr形成压片时，原先的有序结构将被破坏，会形成各种分子聚集体，但由于以氢键结合的二聚体比较牢靠，故该构型将会是占优势的存在形式，所以我们通过二聚体之间存在的作用力模拟其他分子对红外光谱的影响。二聚体中两个羟基应具有相同的振动频率及相同的对称性，具备了费米共振的条件，使得振动频率发生分裂，在非谐振子模型下M06-2X泛函计算的O—H伸缩振动位于3 180以及2 948 cm-1处，而实验值为3 210及2 901 cm-1，误差分别为30以及47 cm-1，羰基的伸缩振动频率实验值为1 675 cm-1, 而M06-2X得到的非谐振频率为1 691 cm-1，吻合得很好, 图7为M06-2X计算得到的二聚体非谐性IR光谱, 图8为固态呋喃甲酸的实验红外光谱, 两者在500～2 000 cm-1范围内不管是红外光谱的强度还是振动频率都较为吻合, 但羟基的透光率计算值与实验值相差较大, 这是由于量子化学对于弱相互作用的计算缺乏合适的参数、普适的力场、合理的色散校正项等因素, 使得计算精度较差造成的, 另外实际固体物质存在的方式多样, 除了此处的的二聚体外, 还存在其他二聚体及多聚体, 这些因素也使计算结果出现偏差； 图7，图8在2 000～3 000 cm-1之间有一些吸收峰，这应该是各种泛频、合频峰，二聚体部分泛频谱数据见附表6。经计算振动量子数对应的0→2红外跃迁的倍频吸收峰强度很小，没有超过1.0 km·mol-1的，而基频之间形成的合频是造成这些峰的主因，如3 190.5 cm-1的峰是1 506.4 cm-1(呋喃环的变形振动)及1 691.1 cm-1(羰基伸缩振动)的和频造成的，对应强度为45.26 km·mol-1，2 851.5 cm-1的峰是1 435.2 cm-1(羟基氢的面内摇摆)及1 424.3 cm-1(羟基氢的面内摇摆)的和频造成的，对应强度为114.18 km·mol-1，2 730.3 cm-1的峰是1 435.2 cm-1(羟基氢的面内摇摆)及1 301.1 cm-1(羟基氢的反对称面内摇摆)的和频造成的，对应强度为60.98 km·mol-1，2 673 cm-1的峰是1 375.2 cm-1(呋喃环上的氢摇摆振动)及1 309.1 cm-1(羟基氢的反对称面内摇摆)的和频造成的，对应强度为37.55 km·mol-1，2 612 cm-1的峰是1 308.2 cm-1(羟基氢的反对称面内摇摆)及1 309.1 cm-1(羟基氢的反对称面内摇摆)的和频造成的，对应强度为40.90 km·mol-1。由于二聚体分子间是通过氢键而不是化学键结合的，其刚性降低，非谐性因素增大，与之相关的合频峰的强度也随之增大，在单体中不太明显的这些峰在二聚体中已很明显，与实验谱图较为吻合。

图7 M06-2X/6-311+G(d, p)下得到的红外光谱

图8 3-呋喃甲酸固相实验红外光谱

Fig.8ThesolidexperimentalIRspectrumof3-furoicacid(quotedfromhttp://202.127.145.134/scdb/)

3 结 论

运用杂化密度泛函及二级微扰方法对3-呋喃甲酸的单体、二聚体构型及红外光谱进行了计算, 进而计算得到了各振动模式的势能分布, 指认了对应的振动模式。利用自然键轨道理论(NBO)讨论了体系中Wiberg键级、C原子的杂化特点、轨道间的相互作用以及二聚体的结合能及二级稳定化能, 探讨了二聚体相互作用的本质。单分子的计算频率与气相分子的实验红外谱图相似，但实际固体中由于存在多种二聚体、多聚体，使得羟基的红外吸收峰变宽且强度降低，尽管缺乏精准的弱相互作用的计算参数及合理的色散校正项，但非谐性条件下二聚体的计算结果与固态谱图较为相符，说明在固态中以氢键结合的二聚体构型占优势。

辅助材料(SupportingInformation)附表1 6-311+G(d, p)基组下3-呋喃甲酸的主要结构参数，附表2 3-呋喃甲酸异构化反应各物种总能量(Et/a.u.)及相对能量(Er/kJ·mol-1)，附表3 B3LYP/6-311+G(d, p)及MP2/6-311+G(d, p)计算获得的3-呋喃甲酸单分子各振动校正后的频率(cm-1), 红外强度(IRint/km·mol-1), PED(%)和振动指认，附表4 二聚体热力学状态函数随温度的变化值，附表5 单体0→2振动跃迁的泛频及强度，附表6 单体、二聚体基频形成的部分合频及强度，附图1 3-呋喃甲酸晶胞，这些材料可以免费从本刊网站上下载。