幂幺和幂等矩阵的一个性质的推广1
2020-01-08潘庆年姚文杰
潘庆年,姚文杰
(惠州学院 数学与大数据学院,广东 惠州 516007)
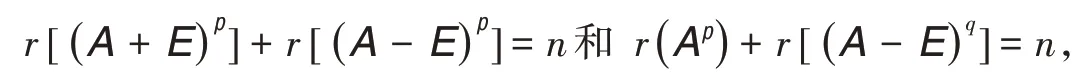
其中,p,q是任意自然数.2010年,文献[3]中给出了幂幺矩阵的一般充要条件

其中,ε0,ε1,…,εm-1是m个m次单位根.2011年,文献[5]中给出了幂等矩阵的一般充要条件

其中,ε1,…,εm-1是m-1个m-1次单位根.
这2个一般条件是否能像文献[2]一样进行推广呢?文章对该问题进行了探讨,并利用相似对角化和线性方程组的解等一些性质,将这2个一般条件进行了推广,并给出了证明.
1 预备知识
1.1 幂幺矩阵的性质
性质1[1]若A为n阶矩阵,且满足
性质2[2]若A为n阶矩阵,满足A2= E,则A可以相似对角化.
性质3[2]若A为n阶矩阵,且满足A2= E,则,其中,p、q是任意自然数.
性质4[3]若A为复数域上一个n阶的方阵且A3= E,则
其中,ε0、ε1、ε2是3次单位根.
性质5[3]若A为n阶方阵且满足A3= E,则方阵A可以相似对角化.
性质6[3]若A为复数域上一个n阶的方阵且Am= E,则

其中,ε0,ε1,…,εm-1是m个m次单位根.
性质7[3]若A为n阶方阵且满足Am= E,则A可以相似对角化.
1.2 幂等矩阵的性质
性质8[1]若A为n阶矩阵,且满足A2= A,则
性质8[2]若A为n阶矩阵,且满足A2= A,则,其中,p,q是任意自然数.
性质9[4]若A为复数域上一个n阶的方阵且A3= A,则
性质10[5]若A为复数域上一个n阶的方阵且Am= A,则

其中,ε1,…,εm-1是m-1个m-1次单位根.
性质11[5]若A为n阶方阵且满足Am= A(m ≥2),则A可以相似对角化.
2 主要结论
定理1 若A为复数域上n阶的方阵且A3= E,则其中,ε0、ε1、ε2是3次单位根,x,y,z是正整数.
证明:由性质5,我们知道A可以相似对角化,则存在一个矩阵P,使得

且对角阵为n阶矩阵.
不妨设A的特征值为a个ε0、b个ε1、c个ε2,则有a + b + c = n.
由

得

得

同理得

综上可得

定理2 (幂幺矩阵秩和定理)若A为复数域上n阶的方阵且Am= E,则

其中,ε0,ε1,…,εm-1是m个m次单位根,k0,k1,…,km-1是正整数.
证明:由性质7,我们知道A可以相似对角化,则存在一个矩阵P,使得
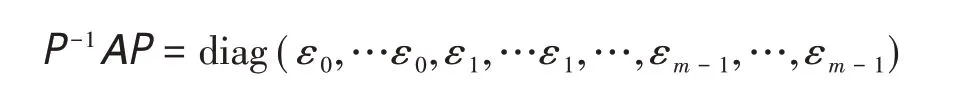
且对角阵为n阶矩阵.
不妨设A的特征值为j0个ε0,j1个ε1,……,jm-1个εm-1,则有j0+ j1+ … + jm-1= n.
由

得

进一步可知

得

同理得

综上可得

类似可得:
定理3 若A为复数域上n阶的方阵且A3= A,则有,其中x,y,z是正整数.
定理4 (幂等矩阵秩和定理)若A为复数域上一个n阶的方阵且Am= A,则有
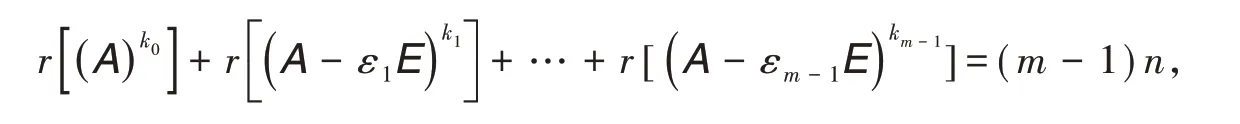
其中,ε1,…,εm-1是m-1个m-1次单位根,k0,k1,…,km-1是正整数.
3 结语
本文推广了2类特殊矩阵幂幺矩阵与幂等矩阵秩的等式,并得到了这2类矩阵秩的等式的2个重要结论.文章对矩阵秩的等式进行了理论上的创新,但其应用价值还有待进一步深入的研究.同时,目前各类出版物及论文上都几乎找不到相应的例题,有兴趣的读者可以进行这方面的工作.最后,读者还可以探索是否可以证明幂零矩阵有类似的结论,可否用文章方法给予证明是一个值得研究的问题.
