等间隔分数时延滤波器及其线性插值设计

赵 慎，杨锁昌，张宝文2，李 元

(1.陆军工程大学石家庄校区，河北 石家庄 050001； 2.中国人民解放军92571部队，海南 三亚 572000)

数字信号精确时延技术广泛应用于阵列信号处理、语音信号处理、声源定位和通信等领域[1]。特别是在宽带雷达和声纳工程中[2]，相控技术在波束扫描时存在有限带宽问题。在大带宽波束扫描时，带内不同频率成分的波束指向不同，同时孔径渡越时间会引起回波信号的畸变，有效的解决方法是采用延时方式代替相位方式进行波束形成[3]。

传统的数字时延方法有过密采样、数字时域内插、频域线性相位加权等[4]，它们的原理都是以时延量化为基础，存在运算量过大或时延精度不高等问题。通过分析传统时延方法，文献[5]对比了几种不同分数时延滤波器的设计原理。工程实际中需对信号进行可变时延滤波处理，以得到期望性能。文献[6]提出了Farrow结构滤波器，实现声纳中的分数时延，首次解决了可变时延的实现问题，但Farrow滤波器系数不存在闭合解，且滤波运算开销高。

分数时延滤波器分为有限冲击响应(FIR)和无限冲击响应(IIR)两大类。其中FIR分数时延滤波器具有稳定性和线性相位优势，在工程中应用广泛[7]。为降低可变分数时延的工程实现复杂度，本文基于FIR滤波设计原则，以理想数字分数时延滤波器原理为基础，分析现有数字分数时延滤波器设计方法，提出等间隔分数时延滤波器设计方法；进一步对相邻滤波器系数线性插值计算，以提高分数时延的精度；对宽带信号进行分数时延仿真，验证方法的正确性和工程价值。

1 理想数字分数时延滤波器

对满足奈奎斯特定理的离散时间信号(采样周期为T)构建如图1所示的理想时延系统[8]。由数字样本序列x(n)重构带限信号xc(t)的系统为理想离散到连续时间(D/C)转换器；连续信号xc(t)通过时延τ的理想系统后得yc(t)=xc(t-τ)；由连续信号yc(t)到数字序列y(n)的系统为理想连续到离散时间(C/D)转换器，且y(n)=yc(nT)。

图1 数字信号时延原理

根据图1中关系得到

y(n)=xc(nT-τ)

(1)

根据理想重构系统定义，带限信号xc(t)与数字序列x(n)的关系为[8]

(2)

其中，sinc(t)=[sin(πt)]/(πt)。将式(2)代入式(1)，得

y(n)=x(n)*sinc[(n-D)T]

(3)

式中，“*”为卷积运算，D=τ/T为数字分数时延。式(3)表明时延滤波器

hid(n)=sinc[(n-D)T]

(4)

当时延τ为采样周期T的整数倍，即D为整数时，退化为特殊形式hid(n)=δ(n-D)，如图2中D=2所示。更普遍情况，时延τ为T的非整数倍，即D为实数时，可以将其分解为

D=Dint+d

(5)

式中，Dint=fix(D)为整数时延，小数d∈[0,1)为分数时延。此时，对于任意n∈Z，均有hid(n)非零，如图2中D=2.7所示。即普遍意义下，分数时延滤波器为无限长的非因果系统。

称式(4)中hid(n)为理想数字分数时延滤波器，其频率响应函数为

Hid(ejω)=e-jωD, |ω|≤π

(6)

幅频和相频响应分别为

|Hid(ejω)|≡1
arg{Hid(ejω)}=-Dω

(7)

普遍意义下，hid(n)为无限长的非因果滤波器。需按照一定原则设计有限长度的因果系统h(n)，逼近理想分数时延滤波器。

2 数字分数时延滤波器设计方法

2.1 最小均方误差设计方法

假定设计出的分数时延滤波器为h(n)，频率响应为H(ejω)，与Hid(ejω)间的误差

E(ejω)=H(ejω)-Hid(ejω)

(8)

最小均方误差(Least Squared Error,LS)方法原则是使得频响误差E(ejω)的L2范数

最小。应用帕斯瓦尔定理，得到时域描述

(9)

进一步分解，得到均方误差

其中N为h(n)的阶数，使得E最小的滤波器系数为

(10)

此即最小均方误差意义下的分数时延滤波器的时域冲击响应。其中，分数时延D与N之间的关系应满足[9]

(N-1)/2≤D≤(N+1)/2

以上hid(n)从零截断，对于从整数M处截断的情况，最小均方误差方法依然可得到类似的结论。此时h(n)仅在N≤n≤N+M存在取值，即

(11)

2.2 约束带宽的最小均方误差设计方法

LS设计原则是使得全带宽[0,π]内均方误差最小。在阵列信号处理、语音信号处理、声源定位等典型工程应用中，感兴趣的信号频谱主要位于中低频段。针对该特性，可约束带宽范围[0,απ]的均方误差

(12)

最小。其中α∈(0,1]为带宽系数。采用与最小均方误差设计方法类似推导过程，得到分数时延滤波器为

(13)

显然，在最小均方误差设计原则下，全带宽是约束带宽条件(α=1)的特殊情况。分析可知，随着α减小，有效带宽逐渐减小，滤波器过渡趋平缓，滤波引起的吉普斯现象逐渐降低。式(12)是在约束频带[0,απ]内，误差积分运算施加矩形窗。部分研究采用平滑过渡窗对误差积分运算进行加权，可改善滤波器幅频特性，然而其代价是引起相频特性非线性化，即造成通带内的时延差异。这种设计方法适用于窄带信号时延处理，但无法满足宽带应用需求。

2.3 加窗设计方法

工程中常采用时域加窗法，使得截断处的滤波器系数经过平缓过渡。加窗设计数字分数时延滤波器为

(14)

其中，w[·]为窗函数。在分数时延滤波器设计中，通常采用切比雪夫或汉明窗函数。

2.4 最大平坦准则逼近法

最大平坦准则是在频域逼近时，使得误差E(ejω)在特定频率处的前N阶导数为零，即

由此得到ω∈[0,π]内的任意频点ω0处误差函数最小的分数时延滤波器系数值近似结果[5]

(15)

该滤波器系数为复数，与相同阶数实数FIR滤波器相比，需要更多的运算量。故一般采取ω=0的结果

(16)

作为最大平坦准则逼近法设计出的滤波器。

3 等间隔分数时延滤波器设计方法

3.1 可变时延需求分析

第2节研究的常规设计方法各有优点，但存在相同的局限性：给定长度和分数时延，滤波器系数为一组固定值。基于该组滤波器系数，仅能适用于固定时延量的应用需求。

在语音信号处理、声源定位、阵列信号处理等应用领域，需要对信号进行可变时延滤波处理，以得到期望效果和性能。针对变时延需求，文献[6]提出了Farrow结构的滤波器，其形式为M组N阶的FIR滤波器，且滤波器系数为分数时延量d的多项式。分数时延滤波器系数随时延d变化，无需重复加载。Farrow滤波器的缺点是阶数大，运算开销高[10]，在工程中难以应用。

3.2 理想等间隔时延量滤波器

等间隔分数时延滤波器的基础是多采样率信号处理理论，其原理如图3所示。

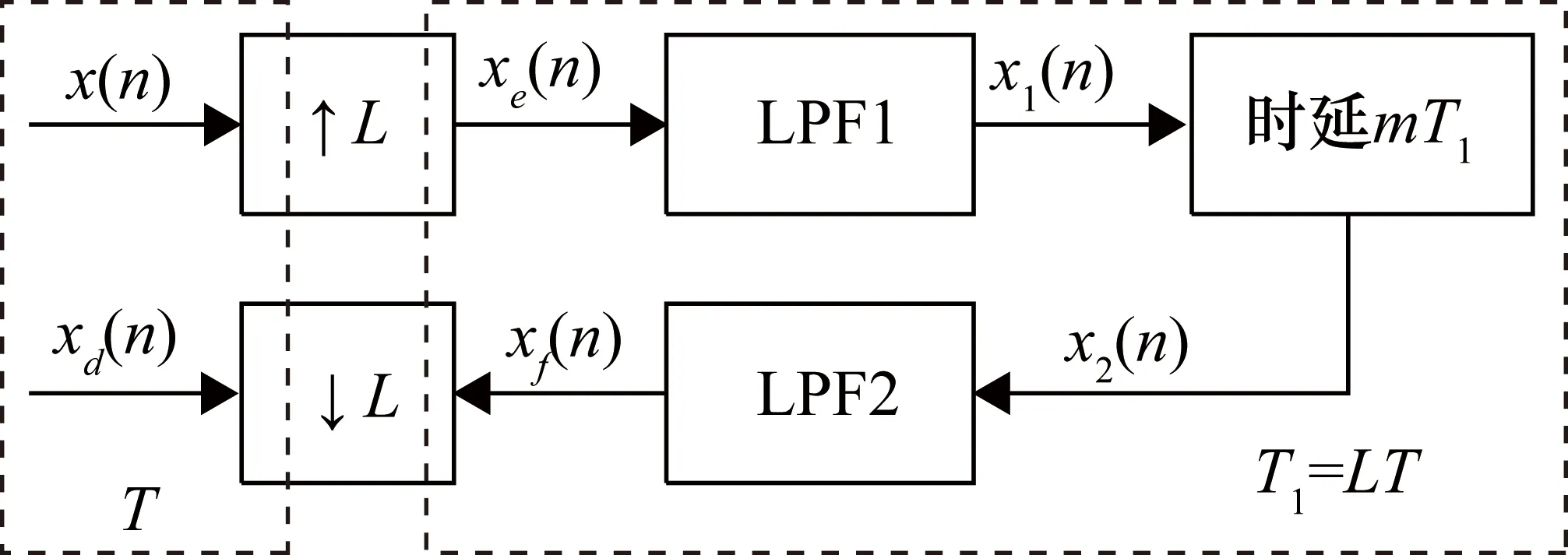
图3 变采样率分数时延滤波原理

x(n)经过L倍增采样和重构滤波器(增益为L，截止频率为π/L)，得到采样周期为T1=T/L的重构信号[8]

x1(n)通过m点延迟取样的输出为x2(n)，即

进一步，x2(n)通过抗混叠滤波和L倍采样率压缩，得到xd(n)=x2(nL)，即

=x(n)*hd,m(n)

(17)

其中，hd,m(n)定义为时延量为d=mT/L分数时延滤波器，延迟输出xd(n)与x(n)之间的时延量为mT/L。分析可知，通过变采样和滤波处理，图3实现的时延精度为原采样周期的1/L。

3.3 等间隔时延量滤波器设计

利用线性时不变系统的结合律，将图3中的重构滤波器、理想时延滤波和抗混叠滤波器级联为单位冲击响应为hm(n)的系统，得到理想等间隔分数时延滤波器

hm(n)=sinc(n-m/L)T, 0≤m≤L-1

(18)

对比式(18)与式(4)可知，hm(n)是理想数字分数时延滤波器在d=m/L时的特殊形式。

式(18)中，hm(n)为无限长非因果滤波器，需按照(约束带宽)最小均方误差、加窗法等原则设计近似有限长度因果系统。不失一般性，以约束带宽的最小均方误差设计方法为例，将d=m/L代入式(13)中，得

hα,m(n)=αsinc[α(n-Dint-m/L)T]

(19)

其中，n∈[M,N+M]，m∈[0,L-1]。M为取样延迟，不影响分析前提下，可取M=0，即n∈[0,N]，则滤波器群时延Dint=N/2。分析可知，等间隔分数时延滤波器为sinc函数时延d=m/L的离散采样。

设系统采样频率为100 kHz，直接延迟取样的时延精度为10 μs。取带宽系数α=1，阶数N=20，插值系数L=10，即设计m={0,1,2,…,L-1}共10组滤波器系数，对应时延分别为τ=DintT+dm，其中分数时延量dm=mT/L，即10个滤波器组的时延量分别为dm=[0 μs,1 μs,2 μs,…,9 μs]。

取所需时延为τ=138.7 μs，可将其分解为：

① 滤波器的固有时延DintT=100 μs；

② 3点延迟取样，即M=3实现30 μs时延；

③ 剩余8.7 μs即所需分数时延，近似选取m=9的滤波器组，取dm=9 μs的分数时延。

因此，可以将所需时延分解为滤波器群时延、取样时延和分数时延。在取样时延基础上，近似选择等间隔分数时延滤波器，实现信号分数时延。

3.4 等间隔时延滤波器插值设计

通过插值选抽处理，等间隔时延滤波器实质是将时延量[0,T]等分为L个相等间隔的格点，其能够实现的最大时延精度为±dm/2。在高分辨率波束、精确时延估计等应用场合，需更精确的时延控制。为此，提出对分数时延滤波器系数线性插值运算，以提高时延精度的方法。

设时延τ分解为整数时延Dint和分数时延d，由于Dint不影响时延精度，故此处集中分析d作用的信号输出xd(n)。取整数

l=fix(d)∈{0,1,2,…,L-1}

(20)

信号经过第l组和l+1组等间隔分数时延滤波器的输出为

(21)

结合物理意义，xd(n)必然位于xl(n)和xl+1(n)之间，可利用线性插值式近似表示

xd(n)≈xl(n)+[xl+1(n)-xl(n)]Δl

(22)

其中，Δl=d-l即d中小数部分。直接应用式(22)计算分数时延输出，需两组卷积运算，为降低运算量，将式(22)带入式(21)中，得到

xd(n)=x(n)⊗[hl(n)Δl+1+hl+1(n)Δl]

记卷积运算的后项为

hd(n)=[hl(n)Δl+1+hl+1(n)Δl]

(23)

则有

xd(n)=x(n)*hd(n)

(24)

总结以上过程，按式(23)计算第l和l+1组等间隔分数时延滤波器的线性组合，得到滤波器hd(n)的系数，计算x(n)与hd(n)的卷积即为输出信号xd(n)。

因此，根据所需的分数时延量，通过等间隔分数时延滤波器系数的线性插值运算，可以得到精确可变时延分数滤波器。

4 算法仿真验证

4.1 等间隔时延滤波仿真

设系统采样频率为100 kHz，线性调频信号x(n)持续时间为5 ms，中心频率为11 kHz，带宽为8 kHz。

取插值系数L=10，构建10组等间隔分数时延滤波器。取带宽系数α=1，滤波器阶数N=20。带入式(19)中，得到10组时延间隔为1 μs滤波器。

信号x(n)通过10组等间隔分数时延滤波器，得到10路时延输出信号x(n-Dint-d)如图4所示，其中d={0.0,0.1,…,0.9}。图中同时绘出直接延迟取样实现DintT和(Dint+1)T时延量的结果，分别表示为x[n-Dint]和x[n-Dint-1]。

图4 延迟取样与等间隔分数时延滤波输出

分析图4(a)可知，10路输出信号与延迟取样信号x[n-Dint]波形基本一致，说明滤波器幅频响应一致性较好，在有效频带内具有线性相位。图4(b)表明输出信号在时间上基本均匀分布在x[n-Dint]和x[n-Dint-1]之间，满足等间隔分数时延特性。有效信号开始和结束阶段，存在明显的吉普斯现象，是最小均方误差准则截断造成的影响。

基于输入和输出信号的互相关函数，并用文献[11]中的抛物线拟合方法确定互相关函数峰值即10路输出信号时延，结果如图5所示。分析表明，10路输出信号的时延量基本满足等间隔关系。

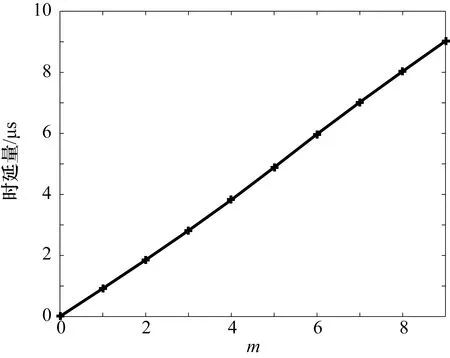
图5 基于互相关计算出的信号时延

进一步，计算输出信号的实际时延与理论时延之间的误差，结果如表1所示。输出信号的时延误差有所不同，最大误差为0.18 μs(小于采样周期的2%)，表明等间隔时延滤波具有较高的时延精度。

表1 L=10组信号时延与理论时延误差 单位:μs

4.2 等间隔时延滤波器插值算法性能仿真

对于任意可变分数时延d，可根据式(20)确定滤波器的序号，并按式(23)进行插值，计算出分数时延滤波器系数hd(n)，然后按式(24)运算以实现分数时延。根据仿真条件，等间隔分数时延滤波器的时延精度为1 μs。取分数时延d在[0,T)区间内、按照步阶量为0.1 μs增长进行仿真验证。采用与4.2节类似的方法评估输出信号时延与理论时延之间的误差，结果如图6所示。

图6 基于线性插值的输出信号时延与理论时延误差

仿真中最大时延误差0.187 μs(小于采样周期的2%)出现在3～4 μs之间，该结论与表1中结果基本吻合。验证了通过插值方法构建滤波器系数方法的有效性，同时说明时延误差和等间隔分数时延滤波器直接相关。分析可知，提高插值选抽因子L和滤波器阶数N，能降低时延误差，但同时会增加硬件存储和运算量开销，实际工程中需要综合考虑允许时延误差和系统资源。

5 结束语

研究了数字分数时延滤波器原理和设计方法，针对固定滤波器系数不能实现可变时延的需求，提出了等间隔分数时延滤波器设计方法，论证了等间隔分数时延滤波的原理和实现结构。为提高时延精度，进一步提出了等间隔时延滤波器线性插值方法构建分数时延滤波器的方法。其滤波计算结构与未插值滤波器的计算结构相同，故在运算量保持不变的前提下，基于等间隔时延滤波器能够实现高精度的可变时延。对线性调频信号的仿真结果表明，在插值系数为10、滤波器阶数为20的条件下，能够实现小于采样周期2%的时延精度，可满足工程中宽带信号高精度可变分数时延滤波需求。