基于EnKF和RSSI的井下人员跟踪定位研究

郭落乐

(晋城煤业集团 寺河矿， 山西 晋城 048205)

煤矿井下作业远离地面，生产系统及地质条件复杂，面临着煤与瓦斯突出、矿井火灾、透水、冒顶等突发事故的威胁，因此，为了保证工作人员的安全，建立一套可靠的井下人员精确定位系统具有重要的意义[1-3].可靠的人员定位对煤矿安全生产和灾后救援工作都能起到积极作用。

当前，发展较为成熟的定位系统(GPS全球定位系统和蜂窝无线定位系统)由于井下巷道系统复杂对电磁波易造成干扰和衰落，增加了井下人员跟踪的难度[4]，并不适用于井下人员定位。随着无线传感器网络( Wire-less Sensor Network，WSN ) 高速发展并且日渐成熟，无线传感器节点逐渐在井下环境设备及人员的定位与跟踪中应用，而常用的定位算法主要是RSSI(接收信号强度)定位算法[5]. RSSI是基于测距的定位算法，其定位结果不具备连续性、递推性和自适应性，无法实时跟踪人员位置并且无法对人员的运动状态进行良好的估计[6]. 井下人员或车辆的运动常为非线性的运动目标，非线性运动的性质增加了井下人员跟踪定位的难度。卡尔曼滤波一般用于线性系统的预测矫正，但当人员做强非线性运动时，卡尔曼滤波的预测矫正性能将得不到发挥。1994年由Geir Evensen提出的集合卡尔曼滤波算法(EnKF)是引入集合预报思想的一种非线性滤波方法，它将集合预报思想和卡尔曼滤波算法结合起来，解决了非线性系统中使用卡尔曼滤波算法的近似问题，适合应用于非线性系统的预测矫正[7,8]. 集合卡尔曼滤波作为一个连续的数据同化(DA)的方法，采用合并模型预测和当前观测值的方式产生一个潜在的系统状态最优估计。由于EnKF具有高效性、可扩展性和易于并行计算的优点，在近几十年内已被广泛应用于地球科学和大气污染以及其他动态状态估计中[9-12]. 本文提出了将集合卡尔曼滤波与RSSI相结合用于井下人员跟踪定位的方法，利用集合卡尔曼滤波减小噪声对定位模型的影响，提高定位的精度。

1 定位方法

1.1 RSSI定位算法

依据RSSI值与距离的特定关系，建立简化的井下人员定位的数学模型为[13]：

RSSI=—(10nlgd+S)

(1)

式中，n为路径损耗系数；d为参考节点与定位节点间的距离；S为当参考节点与定位节点间距离d为1 m时所测得的RSSI值。

在测得参考节点与定位节点间相对精确的距离di后，使用空间距离后方交会法，可以确定定位节点一定在以参考节点为圆心，di为半径的球面上，在得到井下人员即定位节点与3个参考节点之间的距离后，可以得到3个球面，那么3个球面相交的点就是定位节点。

计算得到参考点与定位节点之间的距离为dn，使用其对应的坐标值与距离值可以列出下列方程组：

(2)

在实际应用中可能会由于测量误差的存在，导致方程组(2)的无解，运用全交点质心法作为定位算法，可以将方程组(2)转换成方程组(3)：

(3)

式(3)可简化为：

Kα=s

(4)

其中：

利用最小二乘法求解式(4)，即可得所求定位节点的定位坐标。

1.2 集合卡尔曼滤波模型

集合卡尔曼滤波的系统状态和系统观测可表示为：

x(tk)=M[x(tk-1)]+η

(5)

y(tk)=H[x(tk)]+ε

(6)

式中，x是动力系统的状态向量，tk和tk-1表示时间步，M(x)是人员的运动模型,η是人员运动模型的误差,y是系统的观测向量,H(x)是观测模型，ε是观测误差。

为了满足人员运动状态的非线性和随机性，采用人员运动模型：

(7)

vt=vt-1+at-1t

(8)

at=ωt

(9)

其中，加速度at为随机数，符合一定条件的随机分布，这样不仅实现了运动模型的强非线性，并且更加符合实际的井下人员运动情况；vt为t时刻的人员速度；st为t时刻的人员位置坐标。

观测模型H(x)用于状态向量的矩阵变换，即将状态向量中的参数映射到观测区域。在该实例中，状态向量中仅有人员位置坐标一个参数，同时可观测信息也同样为人员位置坐标，因而H(x)可计算如下：

H(x)=x

(10)

集合卡尔曼滤波模型分为预测和更新两个步骤，分别按下式计算：

(11)

(12)

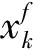
(13)

(14)

Ke=PeHT(HPeHT+Re)-1

(15)

式中，Re是观测误差协方差矩阵，即为观测噪声；Pe是状态预测误差协方差矩阵；N表示集合的数量大小，该实例中取为60. EnKF的误差协方差矩阵通过有限个集合成员得出，用集合的思想解决了卡尔曼滤波算法在非线性运动目标跟踪定位中估计和预测误差协方差矩阵比较困难的问题。

2 定位仿真分析

为了验证该人员定位方法的精确性和实用性，对一个线性运动状态和两个非线性运动状态进行仿真分析。其中两个非线性运动的定位目标中，一个定位目标做加速度a符合(-0.4～0.6)随机分布的变加速运动，另一个定位目标的运动情况符合：匀速运动—加速运动—减速运动—匀速运动，由此，这两个定位目标的运动状态具有了强非线性的特点。为了模拟由于矿井复杂环境及人员运动所造成的电磁波干扰和衰落而导致的定位误差，对线性运动定位目标添加了符合(0～5 m)随机分布的噪声,对非线性运动目标添加了符合(0～10 m)随机分布的噪声。3个定位目标的运动参数设置见表1.

表1 3个定位目标的运动参数设置表

由于在EnKF定位方法的实际操作中，定位目标的真实初始速度不可预测，因此集合卡尔曼滤波模型只能输入一个先验的初始速度，在先验初始速度与真实初始速度之间的误差将通过集合卡尔曼滤波算法利用观测值来进行矫正。在该仿真分析中，设置集合卡尔曼滤波模型的集合数量[7]为60，先验初始速度与真实初始速度的设置见图1.

3个定位目标的定位及定位绝对误差情况见图2，3，4.

图2表明当定位目标为线性运动状态时，EnKF定位模型可以借助RSSI定位算法所得到的位置信息

图1 先验初始速度设置图

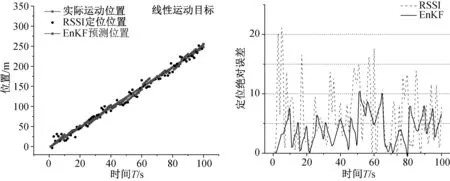
图2 线性运动目标定位情况及误差图

作为观测值，实现对运动目标的连续定位，并且定位精度也得到明显提高。即使给定位目标添加了0～5 m随机分布的噪声，EnKF模型定位的绝对误差绝对值在10 m之内的比例达到了99%，在5 m之内的比例为67%，而RSSI定位绝对误差绝对值在10 m之内的比例只有79%，在5 m之内的比例为46%，与RSSI定位的结果相比较，EnKF模型定位的结果有更良好的参考价值。

从图3和图4中可以看出，EnKF定位模型对两种非线性运动目标的定位效果，由于非线性运动目标定位添加了较大的噪声，并且非线性运动加大了EnKF模型跟踪定位的难度，因此其结果与线性目标定位相比有较大的定位误差。但是由于EnKF定位方法结合了RSSI定位与运动模型，有效减轻了RSSI定位的随机误差，在两种非线性运动目标定位中均取得了比RSSI定位更加精确的结果。其中，非线性运动目标1的EnKF定位绝对误差绝对值小于10 m的比例为64%，小于15 m的比例为90%；非线性运动目

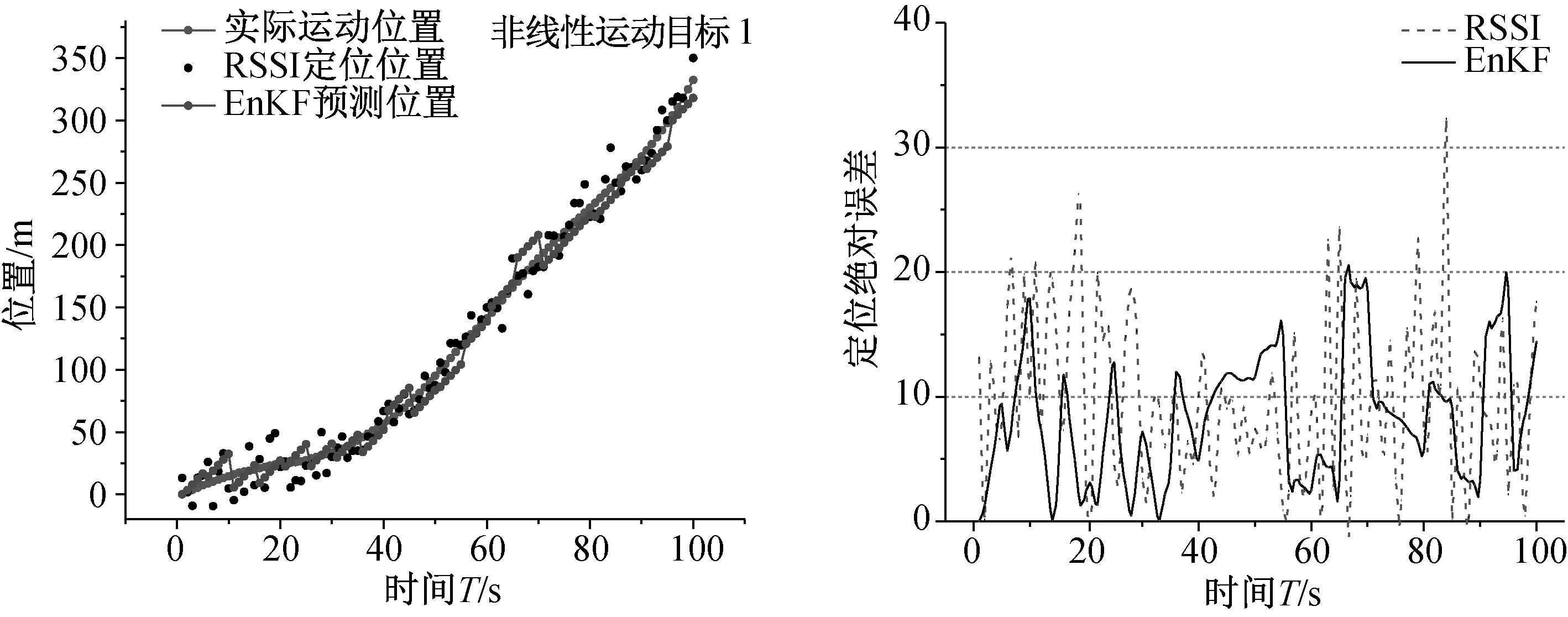
图3 非线性运动目标1的定位情况及误差图

图4 线性运动目标2的定位情况及误差图

标2的EnKF定位绝对误差绝对值小于10 m的比例为70%，小于15 m的比例为96%. 而RSSI对两个非线性运动目标的定位误差绝对值小于10 m的比例分别为58%和54%，小于15 m的比例分别为77%和82%. 因此，EnKF定位模型在井下非线性运动目标定位中同样可以取得比RSSI定位更加精确可靠的结果。

3 敏感性分析

在EnKF定位方法中，先验的初始速度中有很大的不确定性，这很可能对定位的结果造成影响。因此，为了验证该方法的实用性，在非线性运动目标2的定位仿真中对先验的初始速度进行了敏感性分析。使用不同先验初始速度的定位情况及误差见图5.

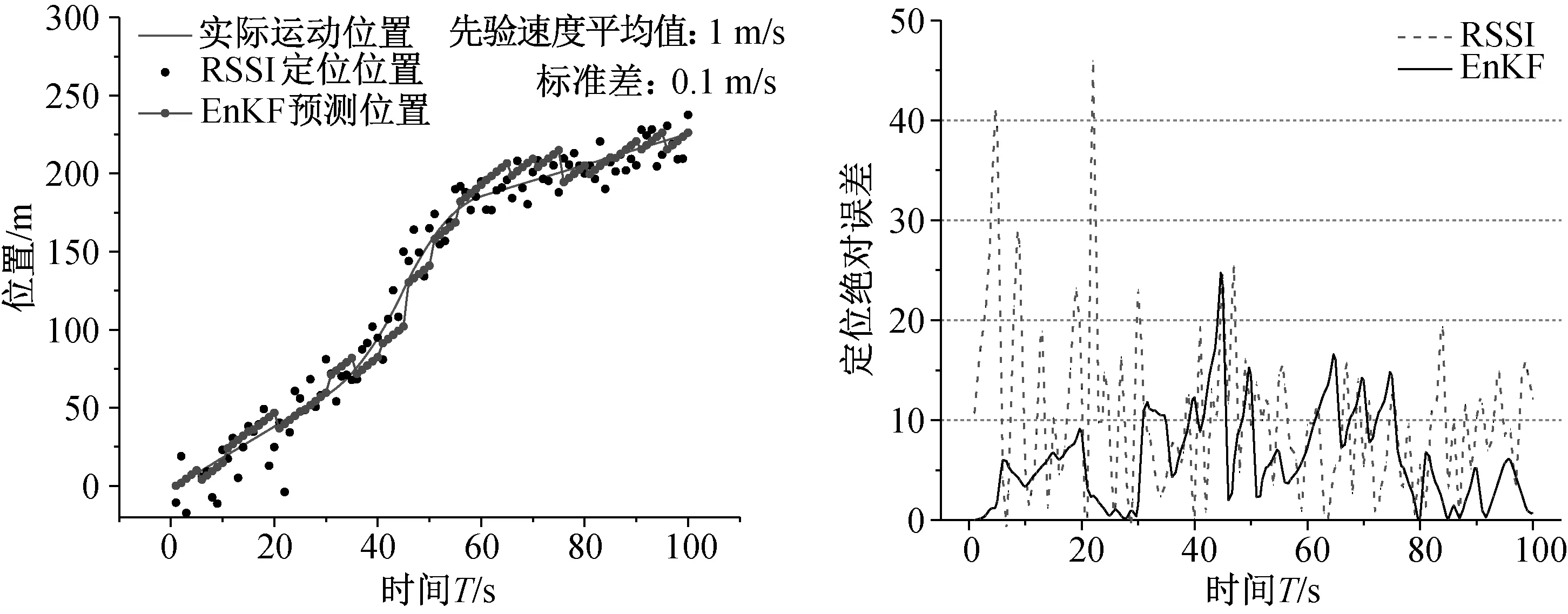
图5 使用不同先验初始速度的定位情况及误差图

从图5中可以看出，当先验初始速度取不同值时，EnKF方法定位的结果均比RSSI定位的结果有所提高。在非线性目标2的定位中，先验初始速度的平均值分别为：4 m/s，3 m/s，2 m/s和1 m/s时，其定位绝对误差绝对值小于10 m的比例分别为：66%、73%、70%和79%，小于15 m的比例分别为：85%、95%、96%和96%. 这说明即使先验初始速度与真实初始速度之间的误差大小不一，通过EnKF算法的预测矫正，在先验初始速度中存在的误差都会被有效抑制，达到精确性类似的跟踪定位结果。因此，该EnKF跟踪定位方法对先验初始速度的敏感性较差，当先验初始速度中含有较多的误差时，依然可以得到较好的定位结果。所以，该方法在井下运动目标的跟踪定位上具有很强的实用价值。

4 结 论

提出了集合卡尔曼滤波(EnKF)与无线信号接收强度(RSSI)定位算法相结合的井下人员跟踪定位方法，该方法通过集合卡尔曼滤波算法减小多种噪声对定位的影响，可得到连续的人员跟踪定位结果。经过仿真实验表明，该方法在线性与非线性运动目标的定位中性能均优于RSSI定位，即使跟踪定位受到较大的误差影响，依然可以取得良好的定位效果。通过先验初始速度的敏感性分析得出，当先验初始速度中含有较多的误差时，该方法依然可以得到较好的定位效果，具有较强的实用性。