高速列车模型参数辨识及控制研究

袁海军， 赵志刚

(兰州交通大学 机电工程学院, 兰州 730070)

高速铁路作为一种节能、环保、高效的复杂运输系统，近年来得到广泛的重视和蓬勃的发展，随着列车运行速度不断提高，轮轨间动力、弓网受流波动加剧和空气阻力增强使得高速列车控制系统面临很多不确定性因素和较大的挑战，人们对高速列车的运行性能和安全性提出了更高的要求。因此对于高速列车的有效建模、优化、控制的研究是保障其安全、稳定运行的基础。

针对高速列车建模、控制问题，国内外学者做了大量的研究。其中，建立适合于列车动态特性的模型是对列车进行控制、设计的前提和关键。文献[1]建立了包含每节车厢的相互作用、暂态影响等因素的多质点单坐标的高速动车组模型。文献[2]考虑了牵引制动等级、各节车厢之间的相互作用力等因素，建立了高速列车多质点模型。文献[3]将多节车厢组成的列车视为一个整体，建立了列车的离散时间运动模型。文献[4]针对高速列车的多质点模型计算量过大的问题，建立了一种计算量适中的单位移多质点模型。

而高速列车是一个具有不确定性、非线性和大滞后性等特点的复杂系统，使得有些变量不能在线直接测量或者测量得到的数据量少而噪声大，故需要研究如何根据少量有效噪声数据辨识得到高速列车特征模型参数，进而建立它的特征模型。例如，目前常规的高速列车动力学建模过程中，许多假设的参数是先验已知的，但是这些参数难以精确获得。而高速列车是一个复杂高阶对象，例如列车的质量由于乘客在不同的车站上下车或者所运货物在不同的货运站装卸可能会发生变化，这就导致许多参数发生了变化，因此为了满足控制性能要求，迫切需要我们找到高速列车控制设计的另一种建模方法。

基于特征模型的建模控制方法[5-9]由吴宏鑫先生首次提出，引起了公众的广泛关注，此后被应用于许多工程实践系统。特征建模方法可以处理精确模型难以获得情况，这种性质确保基于特征模型的方法具有解决高速列车控制设计中许多参数的不确定性，操作环境的不确定性和不可预测性等问题。所谓特征建模，就是结合对象动力学特征、环境特征和控制性能要求进行的建模，而不是仅以对象精确动力学分析建模。特征模型的形式比原动力学方程简单，控制中容易实现。在同样的输入条件下，高速列车特征模型跟原动力学模型在输出上是等价的。而高速列车是一个高阶复杂对象，特征模型可以将高阶模型的有关信息压缩到几个特征参量中，并不丢失原来的信息，一般情况下，特征模型用慢时变差分方程来表示。

对于高速列车这种不确定性大型复杂对象的控制，控制过程不允许在线反复调试，必须要一次成功，或最多可调一两次即能达到希望结果，这样很难用传统的PID控制和自适应控制来解决。而且人为的干扰中断、起停是常事，系统常处于过渡阶段，而这种过渡过程的控制是现有的自适应控制、鲁棒控制和目前的智能控制都感到难办到的事情，然而这也是高速列车控制中不可回避的事实，必须研究这种混杂状态的控制问题。

基于以上分析，文中首先介绍了高速列车的基本动力学模型以及系统设计的控制目标。其次，通过特征建模方法建立了列车特征模型，通过梯度矫正参数辨识方法对模型时变参数进行辨识优化，通过辨识得到的估计值和模型值的对比来验证模型参数对模型精确度的影响。最后，设计了最优控制器和最优PID控制器，通过速度和位置误差跟踪仿真结果来验证控制器的有效性，结果表明所提出的控制方法对特征建模是有效的。

1 高速列车动力学模型

1.1 一般动力学模型

一般来说，高速列车整体动力学模型可以用式(1)～式(4)来描述：

(1)

和M=(1+γ)m

(2)

其中M是列车有效牵引质量，包括列车质量m。γ表示列车回转质量系数，一般取0.06。

Fμ(t)=λ·Ft(t)+(1-λ)·Fb(t)

(3)

λ表示逻辑开关常数，λ=0或1，确保牵引力Ft(t)和制动力Fb(t)不在同一时间内工作。

Fr(t)=mg·(a+bv(t)+cv2(t))

(4)

方程式(4)表示基本阻力，由于列车型号的不同,a、b、c相应的值也不同，一般都是经验所得，考虑到建模和控制器设计的难题，将式(4)采用最小二乘法进行曲线拟合，线性化处理得到：

(5)

图1 基本阻力的最小二乘估计

如图1所示，随着速度的增大，基本阻力相应的也增大，通过选择25个采样点，估计得到式(5)的估计值k和b的值。

(6)

大多数现有控制方法中使用力作为列车控制系统输入,然而这种力不能在列车运行过程中进行直接调整和控制。根据牵引电动机电压和电枢电流与力的关系，由非线性动力学Fu(t)=ψ(Ua(t)，Ia(t))关系可得 ，在列车控制中可以将 作为控制的输入。

列车模型可以用如下动力学方程来表示：

(7)

(8)

Fμ(t)=φCTφIa(t)

(9)

(10)

其中φ=2μcη/D，n(t)=1 000μcv(t)/(60πD)，式(9)表示牵引力与电流的关系，T=CTφIa(t)表示牵引电动机转矩，式(10)表示牵引电动机电压平衡方程。

通过联立式(5)～式(10)可以得到牵引电机电流方程，如式(11)所示：

(11)

对式(11)进行求导得到式(12)：

(12)

整理得：

(13)

因此，列车整体动力学模型可以用式(13)来表示。进一步可以将式(13)表示为：

(14)

其中

通过将式(14)进行拉氏变换得到：

(15)

式(15)为列车单质点动力学模型的传递函数。

各个公式参数的说明见表1。

表1 公式参数说明

1.2 列车控制器设计的目标

1.3 高速列车特征模型

由1.1高速列车单质点一般动力学模型,在满足一定采样周期Δt(Δt可以保证输出误差在允许范围之内)的条件下,当要实现速度保持或者速度跟踪控制时,其特征模型可用一个二阶时变差分方程形式来描述:

v(k)=α1v(k-1)+α2v(k-2)+

β0μa(k-1)+β1μa(k-2)

(16)

对于最小相位系统,根据全系数自适应控制理论[7],工程上一般取β1=0,因此高速列车特征模型可以用式(17)的差分方程来表示:

v(k)=α1v(k-1)+α2v(k-2)+β0μa(k-1)

(17)

其中v(k)表示误差输出；μa(k)表示控制量的输入；α1、α2、β0为慢时变系数。动态过程中,在同样输入 情况下,特征模型的输出和实际对象输出是等价的,慢时变系数在式(18)范围内变动：

(18)

2 特征模型参数辨识

2.1 梯度校正参数辨识

高速列车特征模型可以写成式(19)参数估计方程式：

(19)

其中

φ(k-1)=[v(k-1)v(k-2)μa(k-1)]T

参数估计式采用式(20)梯度算法:

(20)

2.2 特征模型参数辨识仿真说明

所用到的参数如表2所示：

表2 主要参数值

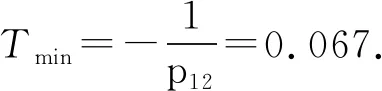
(21)

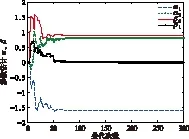
图2 参数α、β的估计结果

由图2可以看出，采用梯度矫正法对特征模型时变系数进行辨识，得到的各个参数辨识结果与模型值基本接近，说明梯度矫正法对模型参数的辨识结果是准确的。

表3 参数α、β的模型值与估计值比较

表3为梯度矫正辨识方法得到的模型值与估计值的比较，模型值通过全系数自适应[7]控制理论方法得到，可以看出模型参数值与实际值之间的误差很小。

3 高速列车二阶系统最优化PID控制器设计

设控制对象为二阶线性定常系统：

(22)

将连续系统离散化：

v(k)=α1v(k-1)+α1v(k-2)+β0ua(k-1)

(23)

将系统化为状态空间模型：

(24)

其中

X(k)=[x1(k)x2(k)]

x1(k)=v(k),x2(k)=x1(k+1)-β0ua(k)

定义新变量：

将状态方程增广为：

AX(k)+Bua(k)

(25)

其中：

离散系统无穷时间二次型最优控制方法设计控制器，取得最优性能指标为:

(26)

其中Q为非负定对称阵，R为正数，若[AB]是完全能控的，则可找到最优控制律：

ua(k)=-LX(k)=-[l1l2l3]X(k)=

-[l1z(k)+l2x1(k)+l3x2(k)]=

(27)

当vr=0，e(k)=vr-v(k)=-v(k)，Δe(k)=-(v(k+1)-v(k))时，最优控制律可以写为：

(28)

由于离散形式的PID控制器为：

(29)

则有：

4 仿真与结果分析

首先将式(14)代入数据离散化得到差分方程为:

v(k)=1.753v(k-1)-0.755 3v(k-2)+

0.000 152 8μa(k)+0.000 139 2μa(k-1)

(30)

因为传递函数为最小相位系统，则特征模型形式为：

v(k)=α1v(k-1)+α2v(k-2)+β0μa(k-1)

(31)

由辨识方法得出α1、α2、β0分别选为1.6、-0.8、0.9,得到它的特征模型为：

v(k)=1.6v(k-1)-0.8v(k-2)+0.9μa(k-1)

(32)

扩展状态矩阵为：

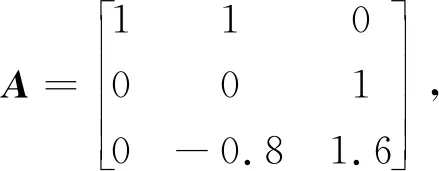
仿真周期为10 s,控制限幅为30,控制的输出速度和位置误差目标值为0，通过优化PID控制器得到：

kp=4.802 5×10-4,

kI=1.000 3×10-6,

kD=8.034 8×10-4

通过Matlab仿真，得到最优控制器下和通过最优控制器优化PID参数得到的PID控制器下的速度跟踪误差曲线和位置跟踪误差曲线：

图3为最优控制器得到的速度和位置误差跟踪曲线，由图可以看出起始阶段速度随着时间的变化，震荡比较剧烈，但经过一段时间以后，速度和位置误差都趋于稳态值，收敛到零，跟踪效果取得了令人比较满意的结果。图4为PID控制器得到的速度和位置误差跟踪曲线，由图可以看出，起始阶段速度随着列车运行时间的变化也发生了较小的震荡，最终也趋于稳态值。不过从图3和图4可以明显的看出，最优PID控制器得到的速度和位移误差相比于最优控制器小很多,都保持在±1 m/s和±1 m范围之内，满足系统控制性能的要求。

图3 最优控制器误差跟踪曲线

图4 最优PID控制器误差跟踪曲线

仿真结果表明：最优PID控制器的控制效果更加良好，满足实际需求，也说明了特征建模和最优PID控制在列车速度和位移跟踪控制中的有效性。

通过仿真得到两种控制器下速度和位置误差的稳态误差、超调量和调节时间3项值如表4所示。

表4 最优控制器性能指标

表5 最优PID控制器性能指标

从表4和表5可以明显的看出，最优PID控制器作用下各项性能指标都比较良好，由此说明了最优PID控制器对列车速度和位置跟踪的有效性。

5 结 论

将基于特征模型的最优PID控制方法引入列车控制系统。(1)分析一般情况下列车的动力学模型，通过选择合适的采样时间建立高速列车速度特征模型；(2)并采用梯度矫正参数辨识算法对特征模型参数辨识，通过辨识得到的估计值和模型值对比来验证模型参数对模型精确度的影响；(3)设计最优控制器和最优PID控制器对列车速度和位置进行误差跟踪控制，通过两种控制方法仿真结果的对比，说明最优PID控制器控制效果更加良好，满足系统控制性能的各项要求。