预制双向孔剪力墙抗震性能有限元分析

李爱影， 张微敬

(北京工业大学 建筑工程学院， 北京 100124)

推广应用装配式剪力墙结构是实现住宅产业化的一个重要途径，有利于实现节能减排、推进绿色安全施工、提高住宅工程质量。上下层相邻预制剪力墙竖向钢筋连接方式对装配式剪力墙结构的抗震性能有着至关重要的影响。文献[1]～[5]分别对竖向钢筋采用套筒灌浆连接、留洞浆锚间接搭接、插筋连接、套筒挤压连接、螺栓连接的预制剪力墙抗震性能进行了试验研究，验证了这5种竖向钢筋连接方式的可靠性。

文献[6]对一种新型预制混凝土双向孔剪力墙(以下简称双向孔剪力墙)进行了低周往复试验研究，结果表明，双向孔剪力墙整体性好，抗震性能满足现行规范的要求。双向孔剪力墙为带有竖孔和横孔的预制板，预制板内配置的水平钢筋为受力钢筋，配置的竖向钢筋为构造钢筋，在预制板的横孔内配置水平插筋，与预制板的水平受力钢筋搭接连接，在预制板的竖孔内配置竖向分布钢筋，相邻层的竖向分布钢筋在楼板标高以上搭接连接。横孔和竖孔用混凝土灌实，使双向空心板成为实体剪力墙。预制板、竖向分布钢筋及水平插筋见图1。

图1 预制板、竖向分布钢筋及水平插筋

有限元数值模拟方法作为试验的有效补充手段已被广泛应用于钢筋混凝土剪力墙结构的研究中，文献[7～9]分别对带水平拼缝、上下插筋连接、以及竖向钢筋套筒浆锚连接的预制混凝土剪力墙的抗震性能进行了数值模拟。双向孔剪力墙是一种新型预制剪力墙，目前的试验研究有限，进行变化参数的非线性数值分析有助于进一步揭示其抗震性能。本文利用有限元软件MSC.MARC对2个压弯破坏的双向孔剪力墙试件进行低周往复荷载和单调荷载作用下的非线性有限元分析，研究轴压比、水平钢筋直径和边缘构件纵筋配筋

率对双向孔剪力墙抗震性能的影响，为双向孔剪力墙的设计和工程应用提供一定的理论依据。

1 试件介绍

2个设计轴压比为0.3、剪跨比分别为1.61和1.81的双向孔剪力墙试件[6]的编号为试件1、试件2，试件高度为2900 mm，墙厚度为200 mm，所采用的预制板板型如图2所示。试件1采用图2a所示预制板，宽度为1400 mm，两端设置宽200 mm的现浇边缘构件，墙体总宽度为1800 mm；试件2采用图2b，2c所示的2块预制板，板宽分别为800，600 mm，采用宽度为200 mm的后浇竖向拼缝连接2块预制板，墙体总宽度为1600 mm，墙体两端为预制板自带的灌孔边缘构件。混凝土强度等级为C30，预制板的横孔和竖孔均用混凝土灌实。试件的参数如表1所示，尺寸及钢筋配置如图3所示。文献[6]对上述2个试件进行了低周往复荷载作用下的拟静力试验，结果表明，2个试件的破坏形态为压弯破坏，水平插筋的配置满足抗剪要求；2个试件正、反向的平均极限位移角分别为1/54和1/56；边缘构件竖向接缝、后浇竖向拼缝的开裂宽度小，接缝两侧构件竖向错动小。

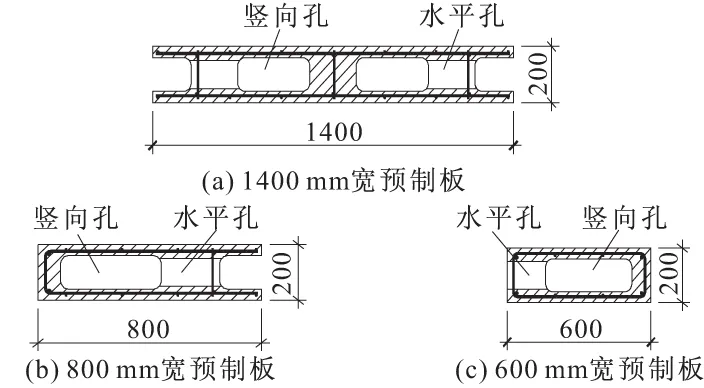
图2 试件预制板板型/mm

表1 试件参数

2 有限元模型建立

2.1 单元类型

采用有限元软件MSC.MARC对2个双向孔剪力墙试件进行建模。混凝土单元和钢筋单元采用分离式模型，混凝土采用Solid7单元模拟，钢筋采用Truss9单元模拟。采用MSC.MARC中的“Inserts”功能直接将钢筋单元嵌入到混凝土单元中，使二者共同作用。地梁与墙体的界面通过弹簧单元模拟。

2.2 材料本构模型

双向孔剪力墙的非边缘构件部分采用非约束混凝土本构模型。此模型选用Hognestad建议的单轴受压应力-应变本构模型[10]，上升段为二次抛物线，下降段为斜直线，如图4a所示，表达式见式(1)(2)。混凝土轴心抗压强度fc取0.76倍混凝土立方体抗压强度试验值。

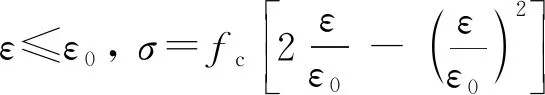
(1)

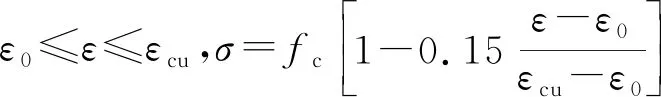
(2)

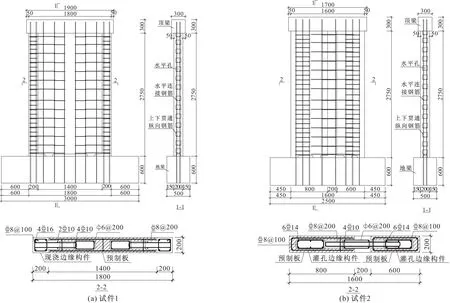
图3 试件几何尺寸及钢筋配置/mm

式中：fc为峰值应力(混凝土轴心抗压强度)；ε0为相应于峰值应力时的应变；εcu为极限压应变。

双向孔剪力墙的现浇边缘构件和灌孔边缘构件采用约束混凝土本构模型——Légeron & Paultre模型[11]，其应力-应变曲线如图4b所示，表达式为式(3)，其中，c0，εc0分别为约束混凝土的受压峰值应力和峰值应变，s，s1，s2为应力-应变曲线的控制参数。

(3)

钢筋单调加载应力-应变关系采用Esmaeily & Xiao模型[12]，该模型由双直线加抛物线三部分组成，分别引入了钢筋的屈服点、硬化起点、应力峰值点和极限点，其曲线形式如图4c所示，关系式见式(4)。

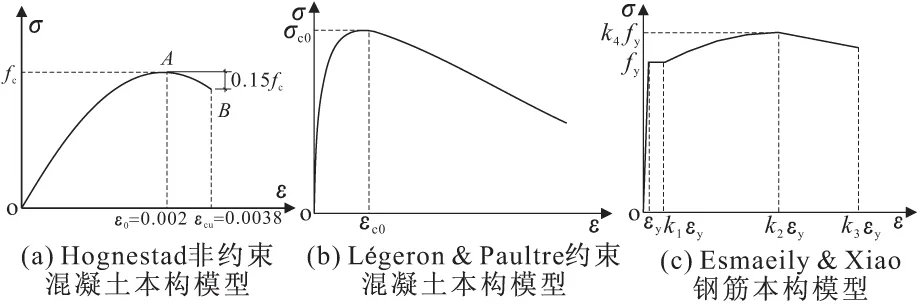
图4 材料本构模型

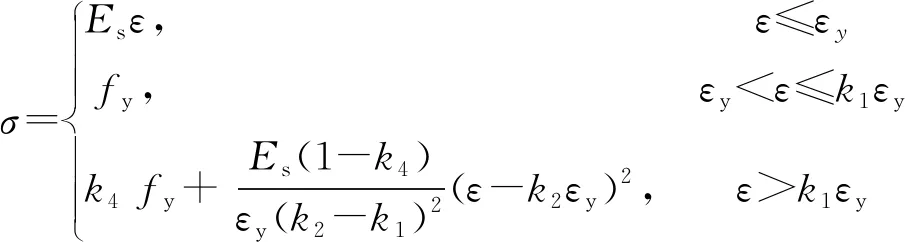
(4)

式中：Es为钢筋的弹性模量，取Es=2×105MPa；fy，εy分别为钢筋抗拉屈服强度、屈服应变；参数k1，k2，k3分别为钢筋硬化起点应变、峰值应变、极限应变与屈服应变的比值，k4为钢筋的强屈比，本文取k1=4，k2=25，k3=40，k4=1.2。

2.3 界面模型

地梁与墙体的界面采用非线性弹簧模拟。法向弹簧的本构关系由混凝土的单轴应力-应变关系简化得到，如图5a所示。其中，ft，fc分别取混凝土的抗拉强度和抗压强度作为界面承载力的极限抗拉强度和极限抗压强度；达到抗拉强度后，弹簧的受拉承载力迅速降为零，弹簧达到抗压强度后承载力保持不变。切向弹簧本构关系采用聂建国等[13]提出的三阶段受力模型，如图5b所示。其中，界面极限抗剪强度τu按式(5)计算，式中：c，μ根据界面粗糙程度按文献[14]确定，σ为界面的正应力，ft为混凝土的抗拉强度；界面的连接钢筋提供的剪应力τr按式(6)计算，假设混凝土失去粘结力后抗剪强度下降为0.5τu，即β取0.5；Sr为界面钢筋屈服时的墙板水平滑移量，Su为极限变形量，Sr，Su依据试验所测数据取值。

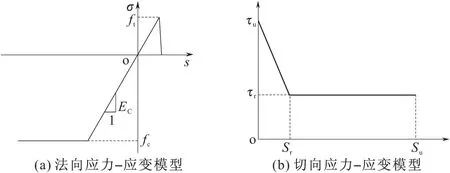
图5 界面模型

(5)

τr=βτu

(6)

3 有限元模拟与试验结果对比

3.1 滞回曲线对比

按低周往复试验中的水平位移加载历程对2个双向孔剪力墙试件进行加载模拟，得到试件顶点水平力-位移/位移角(F-Δ，F-θ)滞回曲线，与试验对比结果如图6所示。由图6，有限元分析曲线与试验曲线均略有“捏缩”，曲线形状基本一致。水平位移较大时，模拟曲线刚度退化不如试验曲线明显，原因在于加载后期试件破坏严重，钢筋与混凝土之间的粘结滑移加剧，而有限元分析中未考虑钢筋与混凝土之间的粘结；此外，试件不可避免地存在加工制作造成的初始缺陷，有限元模型也没有考虑试件的初始缺陷。总体上，模拟与试验滞回曲线吻合良好，表明本文所采用的模拟方法正确、可靠。

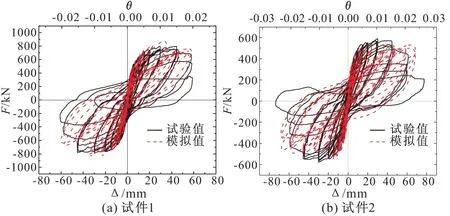
图6 模拟与试验水平力-位移(位移角)滞回曲线比较

3.2 推覆分析

采用上述有限元模型，对2个试件进行推覆分析，推覆分析的预制墙水平力-位移单调曲线与试验骨架曲线如图7所示。以试件1为例，推覆分析极限状态下沿钢筋长度方向的钢筋应力云图、混凝土墙体竖向总应变云图见图8，此时对应的顶点位移为55 mm。由图7，推覆分析单调曲线与试验骨架线吻合良好，最大误差值小于10%，说明推覆分析的计算正确。由图8，墙板两端纵向钢筋应力较大，边缘构件根部混凝土压应变较大，受压破坏较严重，与试验结果一致。

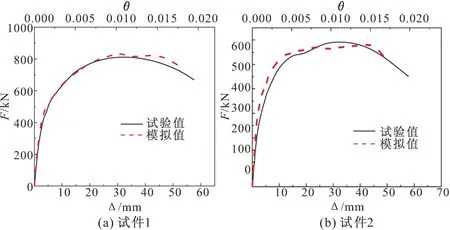
图7 模拟与试验水平力-位移(位移角)曲线比较

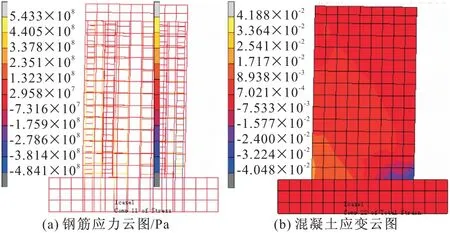
图8 试件1极限状态下钢筋应力、混凝土应变云图

4 参数分析

改变试件参数，进行推覆分析，进一步研究轴压比、水平插筋直径、边缘构件纵筋配筋率对双向孔剪力墙抗震性能的影响。

4.1 轴压比

取设计轴压比为0.1，0.2，0.4，得到试件1和试件2的水平力-位移曲线，结果见图9，图9中设计轴压比为0.3的曲线为试验中试件实测曲线。

由图9：2个试件的水平力-位移曲线变化规律一致，随着轴压比的增大，预制墙的承载力提高；轴压比由0.1增大到0.4，两端为现浇边缘构件的试件1的承载力由667.5 kN提高到874.0 kN，提高了30.9%，两端为灌孔边缘构件的试件2 的承载力由467.9 kN提高到633.7 kN，提高了35.4%。轴压比为0.4的墙体与轴压比为0.3的墙体相比，曲线下降段下降较快。轴压比为0.4时，两端为现浇边缘构件的试件1承载力达到峰值后随即下降；两端为灌孔边缘构件的试件2达到峰值承载力后曲线有一平稳段才下降。可知两端为灌孔边缘构件的试件2变形能力好于两端为现浇边缘构件的试件1，其原因是试件1的边缘构件长为200 mm，而试件2的边缘构件长为400 mm，对混凝土的约束长度大于试件1。

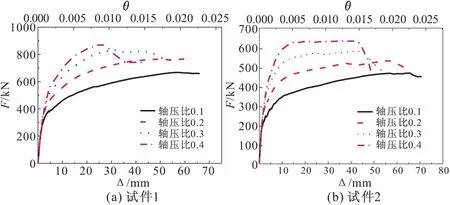
图9 不同轴压比下的水平力-位移(位移角)曲线

4.2 水平插筋

同层相邻双向孔剪力墙水平受力钢筋的连接，是采用“插筋连接”。为研究水平插筋的直径对双向孔剪力墙抗震性能的影响，在设计轴压比为0.3条件下，改变试件的水平插筋直径进行推覆分析。试验试件的水平钢筋直径为8 mm，推覆分析分别取水平钢筋直径为6，10，12 mm，结果如图10所示。

由图10：水平钢筋直径由6 mm增大到12 mm时，试件1的承载力由803.3 kN提高到875.5 kN，提高了8.9%；试件2的水平力-位移曲线基本重合，水平插筋直径对试件2的承载力几乎没有影响；总体上，改变水平插筋直径对两种墙体受力性能影响不大，原因在于试件为压弯破坏，原水平插筋配置满足抗剪要求且偏于安全。

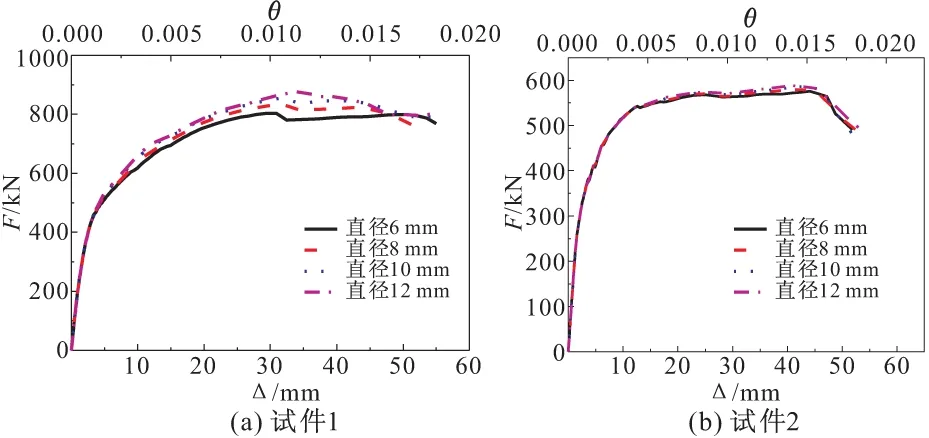
图10 不同水平插筋直径下的水平力-位移(位移角)曲线

4.3 边缘构件纵向钢筋配筋率

双向孔剪力墙的边缘构件包括现浇边缘构件及灌孔边缘构件两种。在设计轴压比为0.3条件下，改变边缘构件纵向钢筋配筋率进行推覆分析。试件1边缘构件纵筋直径为16 mm(配筋率为2.0%)，推覆分析分别取边缘构件纵筋直径为12，14，18 mm(配筋率分别为1.1%，1.5%，2.5%)；试件2边缘构件纵筋直径为14 mm(配筋率为1.2%)，推覆分析分别取边缘构件纵筋直径为12，16，18 mm(配筋率分别为0.8%，1.5%，1.9%)，结果如图11所示。

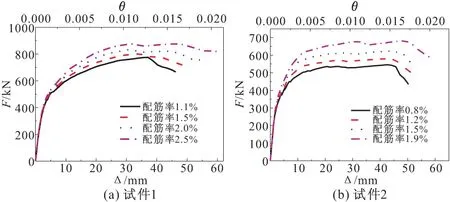
图11 不同边缘构件纵向钢筋配筋率下的水平力-位移(位移角)曲线

由图11，随着边缘构件纵筋配筋率的增大，试件的峰值承载力提高，变形能力增强；试件1边缘构件纵筋配筋率由1.1%增大到2.5%，峰值承载力由776.3 kN提高到876.1 kN，提高了12.8%，试件2边缘构件纵筋配筋率由0.8%增大到1.9%，峰值承载力由545.4 kN提高到682.3 kN，提高了25.1%，增大边缘构件纵筋配筋率对两端为灌孔边缘构件的预制墙承载力提高较大。

5 结 论

通过对2个压弯破坏的双向孔剪力墙试件在低周往复荷载及单调荷载作用下的非线性有限元分析，得出以下结论：

(1)有限元分析的水平力-位移滞回曲线及水平力-位移单调曲线与试验结果吻合良好，表明有限元模型合理、正确；

(2)轴压比对双向孔剪力墙的受力性能影响较大，随着轴压比的增大，预制墙的承载能力提高，变形能力下降；轴压比为0.4时，两端为灌孔边缘构件的预制墙变形能力好于两端为现浇边缘构件的剪力墙；

(3)水平插筋直径对双向孔剪力墙的承载能力影响不大；增大边缘构件纵向钢筋配筋率能提高剪力墙的水平承载能力和变形能力，且此参数对两端为灌孔边缘构件的墙体承载力影响大于两端为现浇边缘构件的墙体。