BIM建模与施工不确定性计算的程序实现
2020-01-08郑俊杰姚翔川
曾 晨, 郑俊杰, 姚翔川
(华中科技大学 土木工程与力学学院, 湖北 武汉 430074)
随着城市建设的飞速发展,利用BIM技术建立三维信息模型,在建筑全生命周期内进行信息共享与交互式工作,实现建筑信息化,已经成为建筑行业的重要发展趋势。
目前,BIM技术主要与结构建筑方面的工程实际结合,在工程管理中应用模型的可视化、参数化和信息化等对项目进行统筹管理。然而,BIM技术的应用范围很广,与监测软件结合能实时监测工程在施工及运行阶段的应力沉降等变化,对复杂环境中的大型工程具有良好的监测效果;将BIM技术与工程计算结合可为建筑项目提供灾前、灾中、灾后安全性分析的预警防控系统,能有效防止灾害的发生和降低灾害的风险和损失。对于深基坑建设中工程繁杂、隐蔽地下导致的潜在问题,建立安全预警防控管理平台尤为重要。因此实现BIM建模和工程计算一体化能有效降低深基坑的工程隐患,提高工程的安全性能,优化施工方案和流程。
针对复杂条件下的地铁车站深基坑工程,要充分考虑工程中存在的不确定性和变异性,综合考量确定性分析和不确定性分析,得到更加符合工程实际的计算结果,以便作出准确的预测,解决深基坑工程中的实际问题。因此实现深基坑工程BIM建模和工程计算一体化,开展软土深基坑力学行为不确定性分析具有极其重要的现实意义和工程应用价值。
1 现有建模分析方法及不足
目前对深基坑安全性能的分析常以极限平衡理论为基础,依据设计图纸进行建模分析。但是实际深基坑工程中存在材料参数的空间变异性和施工支护等施工精度的不确定性,仅仅通过单一土层和标准基坑设计来评价工程的安全性能是不合理的。
深基坑工程中的不确定因素主要来自两方面:(1)材料参数的空间变异性;(2)构件几何形状或位置的不确定性(例如开挖过程中超欠挖的或支撑架设精度的不确定性等)。这两方面的不确定性计算存在较大的差别。空间变异性能通过生成随机场对材料参数进行参数更新得以改善,目前该方面的研究较为系统。Lumb[1]将统计学理论引入土力学,对天然土体中存在的变异性和土体强度的概率分布进行分析,得到抗剪强度参数服从正态分布的结论,并第一次提出了土体参数的空间变异性的概念。Vanmarcke[2]为了描述土体性质的空间变异性,提出了相关距离的概念,并以此为基础建立了土体材料的随机场模型。Bjerrum[3]对基坑支护体系的可靠度进行了研究,分析了不同失效模式下的不确定因素。国内对岩土工程中参数不确定研究发展也较为系统。张继周等[4]通过现场统计数据得出结论:岩土参数接受正态、对数正态分布。唐雨耕[5]以工程实例为基础研究了土体材料的空间变异性对地下支护结构侧移变形的影响。
构件的几何形状和位置的不确定性往往需要根据不同的不确定参数进行网格和节点的调整,在建模上费时费力,因此前人对深基坑工程的不确定性问题中施工精度的不确定性未进行深入研究。但是,在施工中一些人为行为会导致的实际工程与预计模型出现偏差,其中由施工质量缺陷导致事故的情况并不少见[6]。
目前可以利用Revit建立深基坑三维模型,并通过相应的转换接口将其导入到岩土工程计算软件中进行计算[7]。但是大部分转换接口只能转换长方体等方块类型模型[8],此外利用Revit API进行模型转换的接口程序在Revit中修改模型同样费时费力[9]。
基于上述缺陷,本文基于Revit-FLAC3D模型转换接口,提出了一种考虑施工精度的不确定性的算法程序。在Revit中对地铁车站软土深基坑开挖的施工过程进行数值建模,通过Revit API自动对Revit模型中施工精度(如支撑架设精度)等不确定性按一定分布规律进行随机分布,再通过Revit-FLAC3D模型转换接口将模型导入岩土计算软件中,从而对施工精度的不确定性进行分析研究。该方法能够有效地将Revit模型随机进行几何形状和位置的随机化分布,再进行后续的计算分析。最后,基于工程实例,对本文所提出的不确定分析的可行性进行了验证。
2 考虑施工不确定性的BIM建模程序实现
2.1 程序开发环境和流程
本文在Microsoft Visual Studio 2015中采用C#语言进行实时调试,以Microsoft. NET Framework 4.5.2为开发框架,利用Revit API将算法程序应用于Revit模型中。以考虑钢支撑施工精度的不确定性为例, Revit二次开发程序流程如图1所示。首先对当前视图下的所有模型进行遍历,对不同模型进行分类并依次进行编号;然后读取每个模型实例中的几何信息、类型属性以及部分自定义参数和注释;之后对部分带有特定注释的模型实例进行随机化处理,对所有钢支撑的高度进行正态分布排列,并将随机化的钢支撑反映到Revit模型中;最后,将随机化后的实体和类型属性结合形成具有完整信息的实例,并按ANSYS APDL语言格式以及FLAC3D可读取的命令流格式生成TXT文件输出。
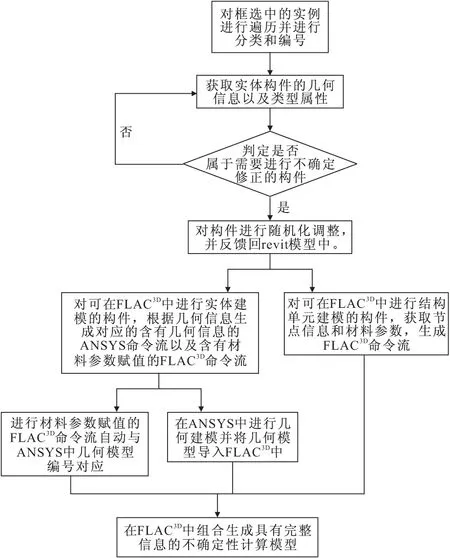
图1 不确定分析接口程序流程
2.2 核心算法主要步骤
首先在Visual Studio 2015的类库工程中对Revit API.dll,Revit APIUI.dll,System. Windows. Forms进行引用,并添加Revit二次开发必要的类型空间,代码如下:
using Autodesk.Revit.UI;
using Autodesk.Revit.DB;
using System.Windows.Forms;
using Autodesk.Revit.UI.Selection;
using Autodesk.Revit.ApplicationServices;//引用Revit二次开发所需要的基础数据库
然后对视图中的所有实例进行遍历,判定其是否属于需要不确定修正的实例,同样以支撑精度的不确定性为例,下例中选取所有名称中带有“钢支撑”的实例,代码如下:
foreach (GeometryObject geomobj in geomElement) //遍历当前视图中所有实体类型
{
GeometryInstance geomInstance = geomobj as GeometryInstance;
Transform instTransform = geomInstance.Transform;
}
foreach (Parameter item in familySymbolParameterList) //对上述遍历结果进行分类
{
FilteredElementCollector collectorFamily = new FilteredElementCollector(doc);
collectorFamily.OfClass(typeof(FamilyInstance));
//判断是否为需要调整的钢支撑结构
if (item.Definition.Name == "说明" && item.AsString() == ("钢支撑" + number1))
}
对判定为需要进行不确定修正的实例进行随机化处理,并反馈回Revit实体模型中,实现对Revit模型的不确定修正:
//生成用于更新支撑高度的随机数,本例中采用正态分布
updata = Random_Normal(miu, sigma, min, max);//生成正态分布的随机数
transaction.Start();
LocationPoint loct = familyInstance.Location as LocationPoint;
//获取钢支撑结构的空间坐标
double x = Convert.ToDouble(loct.Point.X.ToString());//获取钢支撑结构中心点的x坐标
double y = Convert.ToDouble(loct.Point.Y.ToString());//获取钢支撑结构中心点的y坐标
double z = Convert.ToDouble(loct.Point.Z.ToString());//获取钢支撑结构中心点的z坐标
//对支撑高度进行更新,并反馈会模型中
double newz= z * (1 + updata); //根据生成的随机数更新钢支撑结构中心点的z坐标,即支撑高度
XYZ newloct = new XYZ(x, y, newz); //将更新后的钢支撑中心点坐标赋予Revit实体中,实现Revit实体的位置变化
loct.Point = newloct;
transaction.Commit();
public double Normal(double x, double miu, double sigma) //正态分布概率密度函数
{
return 1.0 / (Math.Sqrt(2 * Math.PI) * sigma) * Math.Exp(-1 * (x-miu) * (x-miu) / (2 * sigma * sigma));
}
public double Random_Normal(double miu, double sigma, double min, double max) //产生正态分布随机数,其中miu为数学期望,sigma为标准差,min为该正态分布的下限,max为该正态分布的上限
{
double x;
double dScope;
double y;
do
{
x = AverageRandom(min, max);
y = Normal(x, miu, sigma);
dScope = AverageRandom(0, Normal(miu, miu, sigma));
} while (dScope > y);
return x;
}
对钢支撑的支撑精度进行正态分布的随机化分布后生成的支护结构如图2所示。

图2 考虑支护精度不确定性的支护结构示意
之后重新遍历实例中的几何信息和类型参数,代码如下:
foreach (GeometryObject instobj in geomInstance.SymbolGeometry) //重新遍历当前视图中所有实例
{
//提取实例中的几何参数,并形成ANSYS命令
Solid solid = instobj as Solid;
foreach (Face face in solid.Faces) //遍历实例中所有平面
{
Mesh mesh = face.Triangulate();
foreach (XYZ ii in mesh.Vertices) //遍历平面中所有关键点
{
XYZ point = ii;
XYZ transformedPoint = instTransform.OfPoint(point);
sb.Append(transformedPoint.X.ToString() + ",");
sb.Append(transformedPoint.Y.ToString() + ",");
sb.Append(transformedPoint.Z.ToString());
sb.Append(" ");
continue;//输出遍历得到的关键点坐标,并根据坐标生成ANSYS命令流
}}
//读取实例中的材料库及类型属性,提取其中的材料参数,并形成FLAC3D命令流
foreach (Parameter item2 in familySymbolParameterList)//遍历当前视图中所有实例的内置参数
{
if (item2.Definition.Name == "体积模量")//遍历到体积模量的参数
{
sb.Append("pro bulk " + item.AsValueString() + " range group " + materialnumber);
sb.Append(" ");//将遍历得到的体积模量参数输出成FLAC3D命令流
……
}}}
图3为根据上述程序生成的随机化FLAC3D模型部分示意图,从图中可以看出,原本位于同一高程的钢支撑已经进行正态化重分布。
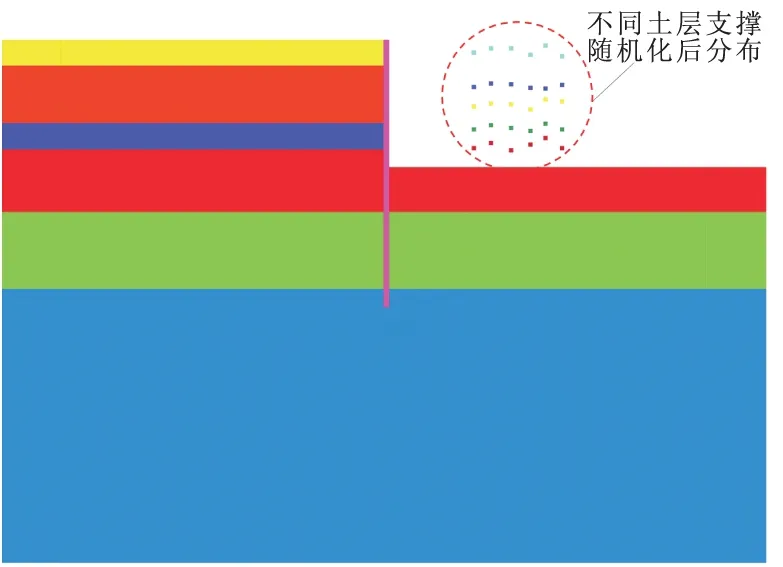
图3 Revit模型随机化处理后导入FLAC3D效果
3 施工不确定性影响的实例分析
基于武汉某地铁车站深基坑开挖实例,针对钢支撑高度这一施工精度的不确定性进行了1000组随机场模拟。表1为最大地表沉降和最大墙体侧移的统计结果,其中最大地表沉降和最大墙体侧移的最大值与平均值相差9.8%和7.6%。可见,人为的施工误差会导致地表沉降和墙体侧移的改变,不过两者相应的变异系数只有2.3%左右,支撑结构的支撑竖向架设位置精度的不确定性对两者影响不大。图4,5为最大地表沉降和地连墙最大水平位移分布频率及正态分布密度函数图,两者都基本符合正态分布,总体的变化范围较小,最大值与最小值之间相差1~1.7 mm。
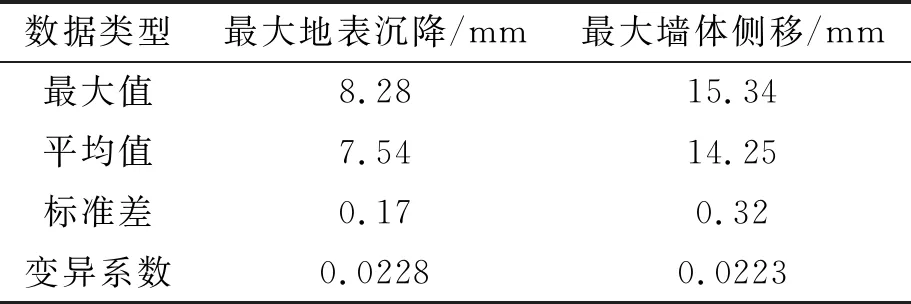
表1 随机场下最大地表沉降和最大墙体侧移数据统计
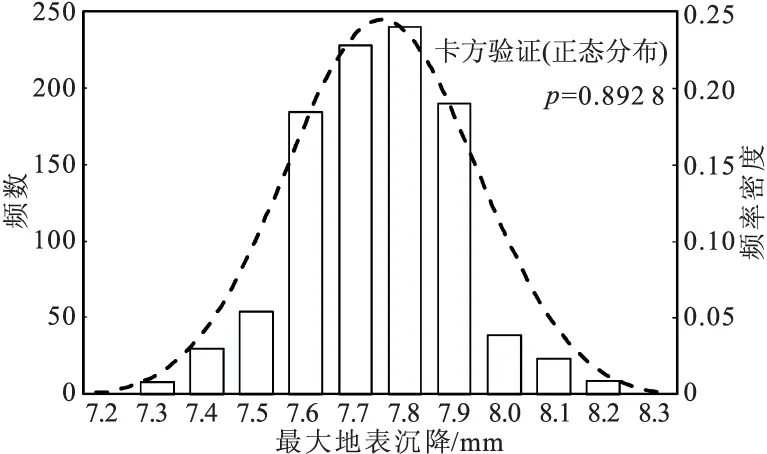
图4 最大地表沉降分布频数及正态分布密度函数
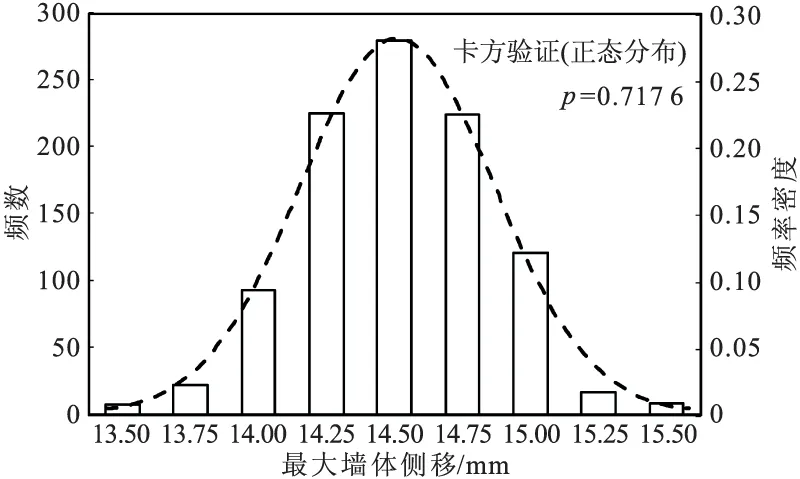
图5 最大墙体侧移分布频数及正态分布密度函数
表2为最大墙体应力和最大支撑轴力的统计结果。从表中数据可知支护结构支撑高度对墙体应力的影响较大,相差为400 kPa。支撑高度对最大支撑轴力有较大的影响,最大值比最小值增大69%,相应的变异系数为7.88%。
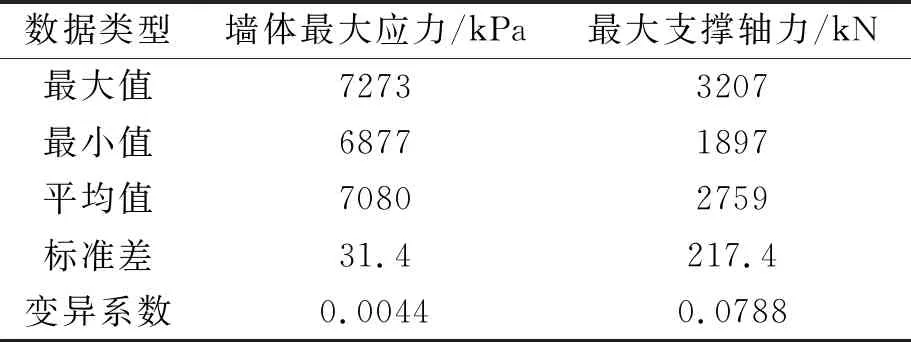
表2 随机场下墙体最大应力和最大支撑轴力数据统计
图6,7分别为地连墙最大应力和最大支撑轴力分布频数及正态分布密度函数图。其中墙体应力基本符合正态分布。最大支撑轴力的最小值为1897 kN,与正态分布的拟合度较差,呈现均值附近频率密度大,两边逐渐减小的特点,可以看出竖向架设精度对支撑轴力的影响很大。
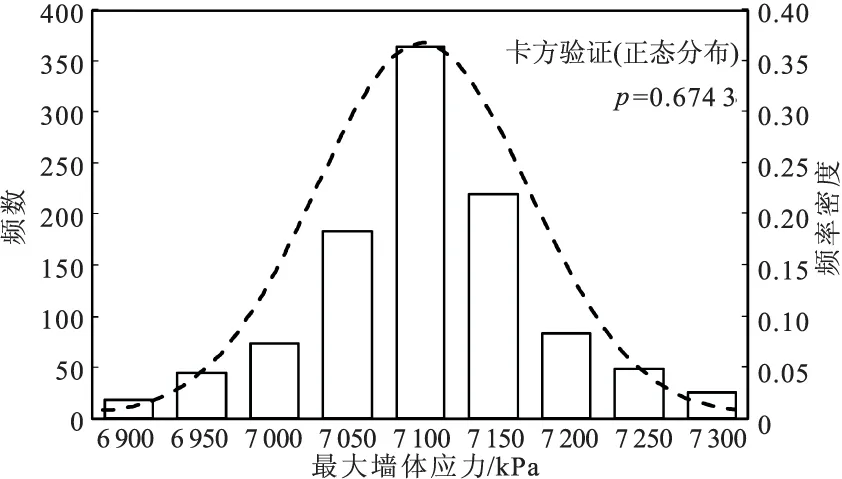
图6 最大墙体应力分布频数及正态分布密度函数
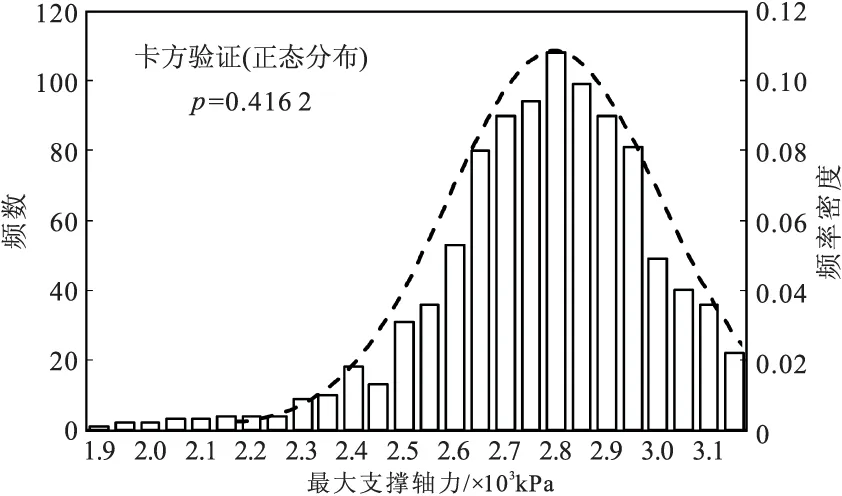
图7 最大支撑轴力分布频数及正态分布密度函数
上述对于钢支撑施工精度的计算结果得到的统计规律与文献[10]一致,从而可以证实该算法程序能在修正不同不确定性因素后实现针对不确定性的计算分析。在考虑岩土材料空间变异性的同时,可针对施工精度的不确定性进行快速建模和计算分析,大大提高计算的效率。
4 结 语
本文利用Revit API技术,编写C#语言程序读取Revit实体模型,对相应实体进行随机化处理并更新模型,通过接口程序将Revit模型导入到FLAC3D中进行计算,实现了考虑施工不确定性的快速建模分析。
基于实际深基坑工程的钢支撑施工不确定性算例验证了算法程序更新后的正确性,能在考虑不确定性的同时,控制模型避免出现过多的偏差。该程序能帮助设计人员对不同施工精度进行分类与建模,简化了计算难度,提高了分析效率。
本文在分析支撑结构高度的不确定性对基坑的影响时,发现其对地表沉降、墙体侧移和墙体应力的影响不大,基本符合正态分布,但对最大支撑轴力的影响较大,最大值约为最小值的1.7倍,因此实际工程中为避免支撑高度对安全性能产生过多影响,应主要以控制支撑轴力为主,保证工程的安全性能。
本文仅以施工精度的不确定性为例进行算法程序的验证,仍有许多地方有待改进。本文中所建立的Revit模型包含了施工中的所有构件,建模耗时较长;同时,进行随机化建模后仍然需要单独计算各类工况,暂时无法实现批量获取计算结果。
