海绵城市建设PPP项目社会资本退出决策
2020-01-08高梅玲黄绵松付德宇
汪 洋, 高梅玲, 黄绵松, 付德宇
(1. 武汉大学 土木建筑工程学院, 湖北 武汉 430072;2. 宁夏首创海绵城市建设发展有限公司, 宁夏 固原 756000)
随着经济社会发展和城市化水平不断提升,城市环境污染、气候变化等全球性问题日益严峻,传统城市生态系统难以抵御此种影响。基于此,我国提出要“建设自然积存、自然渗透、自然净化的海绵城市”,并出台多项举措推进海绵城市建设进程。由于海绵城市建设具有综合性强、复杂程度高和投资规模巨大等特点,项目普遍采用公共和社会资本合作的PPP(Public-Private Partnership)模式。2017年4月财政部发布《关于进一步规范地方政府举债融资行为的通知》(财预[2017]50号),明确禁止地方政府兜底承诺PPP项目社会资本的最低收益。加之,金融市场监管日趋严格,建设资金投入日趋紧张增添了PPP项目的融资难度。据统计,截止至2018年6月,全国统计在库的PPP项目共计7749个,项目落地率仅为47.3%[1]。落地难、投资回收期长和社会资本退出机制不明晰成为阻碍社会资本参与PPP项目的重要因素。
相关研究表明,约20%的PPP投资人会提前退出项目的建设和运营[2]。对社会资本而言,确定适宜的退出时机和退出方式可有效防范工程投融资风险,有利于更好地促进政府和私人资本合作共赢。本研究以在建的宁夏回族自治区固原市海绵城市建设为例探讨PPP项目社会资本退出机制,通过构建基于价值损益理论的社会资本退出决策模型,研究PPP模式下社会资本在海绵城市建设项目中的退出时机和方式选择,为社会资本有效规避工程资金风险提供理论依据和实践操作意义,并为政府制定相关的退出机制和政策提供参考。
1 研究现状
近年来,海绵城市逐步升级成为城市建设领域的国家战略,而建设领域推行PPP模式仍处于创新探索的重要阶段,针对海绵城市建设PPP项目,构建成熟的社会资本退出机制意义重大。国内外学者从多方面研究了PPP投资项目的社会资本退出方式和时机。
PPP项目社会资本退出方式的研究主要聚焦于典型的权益转移与交付方式。Giot等[3]建立了生存风险模型,根据IPO、股权转让和清算三种退出方式成本损益的差异进行选择;张国[4]从主动和被动退出两个方面总结了当前社会资本退出路径,并阐述了各自的适用范围;徐志超等[5]从经济性均衡的角度,提出了城市轨道交通类PPP项目企业的柔性退出机制及具体优化策略;曹启龙等[6]认为社会资本投资的收益变动符合几何布朗运动,通过模型求解出社会资本在政府给予不同等级补偿下的退出临界值,并验证了模型的可用性。
PPP项目社会资本退出时机的研究关注其影响因素和最优时机的决策问题。Cumming等[7]认为企业退出时间受其内外部因素的影响,如资本运作状况、融资能力和信息不对称等;而Bienz[8]认为任一投资项目中社会资本都有一个最优的退出时机;孙慧[9]运用现金流折现模型对社会资本退出的财务可行性进行评价并分析关键变量对退出时机的影响。
综上,学者们就退出方式的特征、适用范围、影响因素等展开讨论,部分研究以数理分析建立损益函数明确社会资本的退出时机。然而,大多数研究是基于某个时点的单一和静态分析,鲜有研究将社会资本的最佳退出时机和方式相联系。鉴于此,本文拟从社会资本的收益入手,依据海绵城市建设PPP项目生产经营中的现金流变化,构建PPP项目社会资本退出方式和退出时机兼顾社会资本方的利益的退出决策模型,寻求社会资本退出时间和退出方式的最优组合,以促进PPP项目社会资本的良性退出。
2 退出时机的一般理论模型
2.1 模型基本假设描述
假设PPP项目中社会资本是风险中性的,政府出资方和社会资本方约定合约到期后,社会资本具有足够的控制权退出该PPP项目。退出时,双方按照股权比例(α∶(1-α))分配该项目收益。
(1)假设社会资本方投资参与该PPP项目的判定标准是:单位时间内获得的收益大于等于某一数值p*。若社会资本方A投资参与了该PPP项目,表明社会资本预期运营期间单位时间内的收益p大于或等于p*。假设单位时间内社会资本的收益来源为PPP项目的经营收益p(p≥p*)和政府补偿g。
(2)PPP项目特许经营阶段,假设单位时间内,社会资本获得经营收益为p和相应付出的经营成本为c,同时产品的需求量为q,由此PPP项目经营运作的利润为(p-c)q。
(3)PPP项目具有不确定性,如未来收益的不确定性和投资方的风险偏好不同,按照McDonald和Siegel的研究,假定PPP项目在t阶段经营运作的现金流量pt服从几何布朗运动,即:dpt=μptdt+σptdzt(μ,σ分别为项目收益的平均增长率和反映项目收益不确定性的方差参数,σ和μ为常数;ρ为风险调整折现率,ρ为常数且ρ>0,确保分析有意义,假设ρ>μ;dzt是布朗运动变化过程中产生的增量)[10]。同理,在经营阶段该项目的收益价值为V(pt,g),社会资本总收益的变动趋势为dt时间内的[rg+(pt-c)q]dt(r为无风险利率,且r>μ)[6]。
(4)PPP项目的最终收益价值具体表现为各阶段收益流rg+(pt-c)q的折现值之和。根据期望定义有:
(1)
式中:τ为时间变量。
(5)经营期内,即使一段时间内社会资本方获得的收益p小于其经营成本c,由于补偿期内社会资本会获得政府的补偿收益,继而会继续经营一段时间。若直到补偿期满,社会资本获得的收益仍然低于成本,社会资本不得不退出项目的运营,假定此时社会资本退出的临界值为p*,社会资本退出后,项目由政府方或其他投资人继续经营,项目的残值为0。
2.2 退出时机一般模型的构建
通常,项目t阶段社会资本方在退出时机决策过程中面临二元选择:立刻退出或继续经营到下一阶段t+1,同时与政府方谈判以期获得更多的补偿。在下一阶段t+1,社会资本会面临同样的二元选择。
在t阶段,当社会资本选择立即退出时PPP项目终止,此时社会资本退出的损益函数为V(pt,g),取决于社会资本退出时产生的收益和费用。而社会资本继续经营到下一阶段,表明社会资本看好该PPP项目的后续发展并选择继续经营到下一阶段。同样地,项目产生的收益价值为各阶段现金流的折现值之和,用Ft(pt,g)表示继续经营时社会资本的损益函数。此时,社会资本不仅可获得t阶段现金流量的α比例,还可以获得以后经营的所有现金流量收益价值的相应份额。t+1阶段,社会资本的损益函数Ft+1(pt+1,g)和Ft(pt,g)拥有一样的函数表达式,且符合动态规划过程。
同样地,根据期望定义,t阶段以后的现金流期望值为Et(Ft+1(pt+1,g)),该损益函数是一阶连续函数,从t+1阶段折现到t的折现因子为(1+ρ)-1。因此,t阶段社会资本的收益为当期和后期现金流之和,即α[rg+(pt-c)q]+(1+ρ)-1·Et(Ft+1(pt+1,g))。因此,t阶段社会资本选择继续经营PPP项目时,其最优退出时机的损益函数

(2)
在这个二元选择过程中,社会资本退出决策的依据是损益函数的最大值。鉴于继续经营PPP项目的损益函数是一个连续函数,在时间长度Δt内,将立即退出和继续经营PPP项目的损益函数相结合,可得到整个过程中社会资本的退出损益函数为一个Bellman方程。即:
(1+ρdt)-1EtF(pt+dp,t+dt)|pt}
(3)
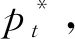
根据伊藤引理可得到PPP项目社会资本退出的损益函数的偏微分方程为:
(4)
依据Dixit和Pindyck的研究结论[11],当现金流量pt的变化过程服从几何布朗分布,所得损益函数偏微分方程解的形式为:
(5)

对于F,当pt→0时,该PPP项目对社会资本而言几乎没收益,为使pt→方程有解,令h1=0。因此,根据文中所提假设,可得社会资本退出的临界值,即pt=p*时,项目对于社会资本的价值得
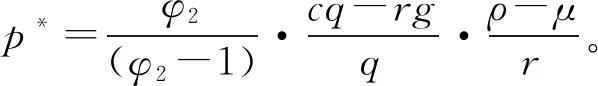
综上,可得到社会资本在不同阶段的收益函数形式为:
F(pt,g)=
(6)
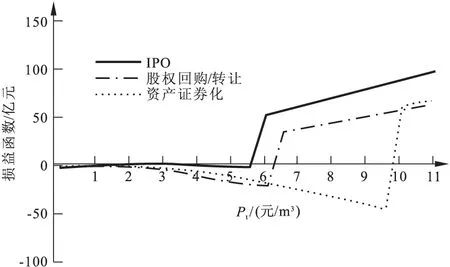
在t阶段,当pt≥p*时,社会资本选择立即退出;而当pt PPP项目中社会资本主要退出方式包括公开上市(Initial Public Offerings,IPO)、股权回购/转让、资产证券化和清算四种,而社会资本退出PPP项目的成本收益会因退出方式不同而存在差异。理论上,清算方式除外的三种退出方式不会影响PPP项目的正常运营。PPP项目中社会资本的退出过程实质为投资者通过某种方式替换控制该项目后续运作的过程。对于PPP项目的现金流pt,不同的投资者具有不同的风险偏好。基于此,本文假定利用折现率来表示不同退出方式下此种风险偏好的不同,IPO、股权回购/转让、资产证券化的相应折现率分别为ρI,ρB,ρA,通常有ρI<ρB<ρ且ρI<ρA[12]。因此,PPP项目社会资本考虑退出方式差异性的损益函数即为不同折现率ρ下对经营活动产生的现金流量pt的折现。 根据PPP项目社会资本退出时机的一般模型,结合不同的退出方式的退出费用函数,可得考虑退出方式差异的PPP项目社会资本可获得的价值损益函数。IPO方式退出为: 股权回购/转让方式退出为: 资产证券化方式退出为: 因此,考虑退出方式差异时的社会资本退出PPP项目的临界值p*如表1所示。 表1 不同退出方式下的社会资本退出临界值 通常在政府方同意情况下,社会资本方进行决策时,应同时考虑退出时机和退出方式。根据建设项目实际情况确定上文模型参数,以此计算不同退出方式下其损益函数F(pt)和退出临界值p*。 通过上述参数可得不同退出方式下社会资本退出PPP项目的收益函数,社会资本在保证收益的同时,其最佳的退出方式取决于不同退出方式下的损益函数:max{FI(pt),FB(pt),FA(pt)},即在该退出方式的临界值上,收益函数最大方式即为社会资本方的最佳退出方式。 固原市地处宁夏回族自治区南部,是全国第二批海绵城市建设试点城市之一。研究社会资本的合理退出路径和退出时机,有利于推进海绵城市建设PPP项目的良好运作。 因此,本文以固原市为例,对海绵城市建设PPP项目社会资本退出决策进行讨论。 固原市海绵城市PPP项目(以下简称“本项目”)建设试点,拟开展海绵城市试点建设的区域面积23 km2,总投资约50亿元,一期投资30亿元。除海绵型建筑小区改建项目外,其他均为污水处理和城市给排水管网等新建项目,综合考虑项目收费机制、项目投资收益水平、风险分配、融资需求和期满处置等因素,采用BOT+ROT模式。双方协商确定,政府方出资代表出资入股比例为项目资本金的20%,市住房和城乡建设局代表市人民政府与社会资本签订PPP项目协议,由项目公司负责PPP合作期内固原市海绵城市的融资、建设与运营维护,PPP合作期25年(含2.5年建设期),PPP合作期满,项目无偿移交政府或其指定机构。 (1)模型相关参数的设定。模型设定相关参数如下:风险调整折现率由无风险报酬率和风险报酬率两部分组成,实际项目根据参考文献[14]调整,参数ρ=0.2;项目价值的平均增长率可利用项目净现金流的增长来表示,参数μ=0.12;反映项目价值的不确定性的方差参数可通过净现值的波动情况计算,参数σ=0.2;风险调整折现率ρI,ρB,ρA反映的是不同投资者针对该PPP项目的风险偏好,根据相关研究的模拟值结合实际项目调整为ρI=0.16,ρB=0.18,由于ρI<ρA,假定ρA=0.17[12,14];一般地,风险调整折现率ρ>r>μ,则令r=0.15。根据公式求解可得φ2=1.513。 (2)其他数值的确定。根据该PPP项目合同约定,政府方和社会资本方按2∶8比例出资,社会资本股权份额α=0.8;特许经营阶段平均每年政府补偿g=18204万元;特许经营阶段每年度的运营成本总额为6867.58万元,需求量q=4800万m3和相应的每m3产品对应的经营成本约为c=1.43元/m3。三种退出方式费用损益的参数:IPO方式的退出费用CI=30000万元,承销费用率ω=0.07;相关文献表明CI>15CB,则股权回购/转让的协商成本CB=2000万元,由于资产证券化对项目现金流高于IPO,于是假定资产证券化的评估成本CA=40000万元,基础资产折让费率φ=0.1。 图1 考虑退出方式差异社会资本退出的决策分析 固原海绵城市建设PPP项目的现金流量来源于特许经营期内的使用者付费的和政府补贴的现金流,具备采用IPO方式退出的基础条件,同时也具备采用资产证券化方式退出的实施条件。国内PPP项目成功采用IPO方式或者资产证券化退出的成功案例较少,典型的代表案例为云南水务集团公司[15]。 由于海绵城市等PPP项目公益性较强而投资巨大,项目运营期内现金流不确定风险较大,考虑操作实施的可操作性和难度等, PPP项目实际运营操作中,IPO退出方式对项目本身有诸多要求,包括社会资本方的资信、建设项目发展前景及运营期内预期稳定的现金流等,这都为PPP项目采用IPO、资产证券化等方式退出设置了较大的门槛限制。因而,社会资本方常选择股权回购/转让或更新改造与再谈判的方式实现资本退出。 本文假定社会资本在项目经营期拥有足够的控制权决定其何时和采取何种方式退出,模型有效地结合社会资本的退出时机和退出方式,动态研究海绵城市建设PPP项目社会资本退出决策问题,并以固原海绵城市PPP项目为案例仿真计算,对社会资本有效退出海绵城市建设PPP项目的决策问题具有探索意义。需指出,实际项目经营期中,社会资本的退出决策由政府方和社会资本方双方共同控制,文中并未考虑双方主导地位的差异,有待下一步深入研究。最后,由于海绵城市建设涉及项目众多、投资巨大、公益性明显等特点,海绵城市PPP项目运营期内现金流不确定风险较大,较为特殊,对于其他有良好固定收益的、无须政府补贴的PPP项目,无须考虑政府补贴即可。 本文相关参数的假定主要基于项目的实际数据做了相应的调整,而关于各种折现率的大小是参照文献[12,14]结论给出的模拟值进行相应的调整。3 考虑退出方式差异性的退出时机
3.1 退出方式差异产生不同价值损益
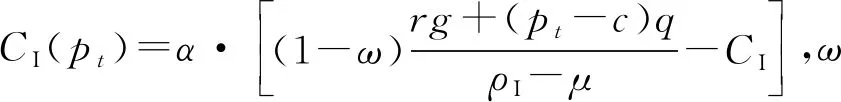
3.2 不同退出方式的社会资本退出时机



3.3 PPP项目社会资本退出方式的选择
4 案例分析
4.1 案例选择
4.2 海绵城市建设PPP项目概况
4.3 PPP建设项目模型参数确定
4.4 退出方式损益函数与退出决策
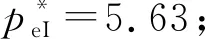

4.5 PPP项目社会资本退出方式的可行性分析
5 结 语
