基于ANM的宽带非相干子空间DOA估计方法
2020-01-08张群飞毛琳琳史文涛王伟东
石 娟,张群飞,毛琳琳,史文涛,王伟东
(1.西北工业大学航海学院,陕西 西安 710072;2.中国科学院声学研究所,北京 100190)
0 引言
波达方位(Direction of Arrival,DOA)估计是阵列信号处理重要的研究内容之一,其应用涉及雷达、通信、声纳、勘探等众多工程领域[1-2]。DOA估计方法主要包括子空间分类方法和子空间拟合方法。目前,比较成熟、稳定的DOA估计方法大都是基于阵列的空间谱估计方法,如多重信号分类方法(Multiple Signal Classification,MUSIC)和旋转不变子空间方法(Estimation of Signal Parameters via Rotational Invariance Techniques,ESPRIT)等,以它们为代表的空间谱方法突破了瑞利限,使测向定位技术实现了飞跃[3]。但这些方法的实现需要大量独立同分布的测量数据(大快拍数据)。在实际环境中,获取大快拍数据受到时间的制约,如高速运转的目标对系统实时性要求很高,尤其在处理超宽带窄脉冲等短时突发数据时,接收信号经过相干累积后只有小快拍数据乃至单快拍数据,无法直接用常规的DOA估计方法进行方位估计。因此,研究小快拍乃至单快拍的DOA估计便是一种有效解决方案。文献[4]提出了单快拍下基于匹配跟踪的ESPRIT的方位估计方法。文献[5]中提出了单快拍及多快拍下联合Matrix Pencil 和 ESPRIT的方位估计方法。随着压缩感知技术的发展,稀疏重构的思想被用于DOA估计中[6],然而,稀疏重构方法对网格划分比较敏感,容易造成信号基失配。为了解决信号失配问题, Tang. 等人提出了基于最小原子范数(Atomic Norm Minimization,ANM)的无网格压缩感知理论[7]。ANM是一种结构优化方法,其基于阵列流型矩阵的范德蒙结构,通过半正定规划(Semidefinite Programming,SDP)可以构造恢复出所需的Toeplitz矩阵。目前,国内外已有不少基于ANM 的DOA估计的研究,如文献[8—9],这些方法都是基于窄带信号DOA估计的研究。
众所周知,在实际应用中,宽带信号源大量存在,并且它能够提供比窄带更多的信息,有利于目标信号检测、参数估计和特征提取[10]。目前,宽带信号处理方法的研究主要基于两大类[10]:一类是基于非相干合成的宽带处理方法(Incoherent Signal Subspace Method,ISM),如文献[11]提出了基于归一化的克拉美罗界(Cramer-Rao bound, CRB)加权非相干宽带DOA估计方法;另一类是基于相干合成的宽带处理方法(Coherent Signal Subspace Method,CSM),如文献[12]提出了一种基于加权拟合的相干处理的子空间宽带信号DOA估计方法。然而,这两种宽带处理的子空间DOA估计方法的实现都依赖于大快拍数据,无法直接有效的处理小块拍数据。
本文为了解决宽带信号在单快拍下的DOA估计失效问题,提出了基于ANM的宽带非相干子空间DOA估计方法(Atomic Norm Minimization Incoherent Subspace Method,A-ISM)。该方法利用子带阵列流型矩阵的范德蒙结构,对每个子带分别进行ANM结构优化,再利用Root-Music算法来估计角度,最后将子带估计结果的均值作为方位估计结果。
文中(·)T、(·)H分别表示转置和共轭转置运算、tr(·)表示矩阵求迹运算、‖·‖为范数运算、‖a‖2表示a的2范数、‖A‖F代表矩阵A的Frobenius范数,E[·]表示期望运算。
1 宽带信号模型和非相干子空间方法
1.1 宽带信号模型
假设观测空间存在K个远场宽带信号(θ1,θ2,…,θK)入射到M元均匀线阵(M>K),其中,θk表示第个k信号的入射角,如图1所示。假设阵列接收的信号不存在相关性,各阵元间噪声相互独立,且为平稳、零均值的高斯空间白噪声,其方差为σ2。
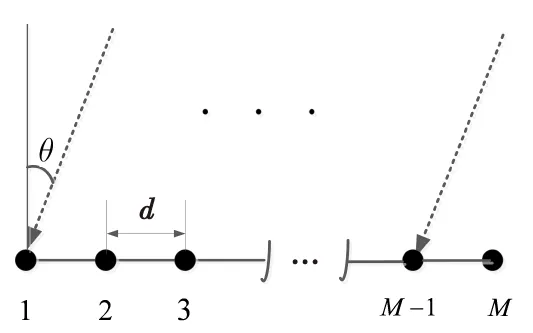
图1 阵列结构Fig.1 Array structure
文中假设信号源的个数已知,且宽带信号的工作频率在[fl,fh]之间,则第m个阵元在第t时刻接收到的数据可以表示为:
(1)
式(1)中,sk和wm分别表示第m阵元接收到来自第k个信号源的信号和噪声,τm(θk)表示位于θk的目标入射到第m阵元和相对于参考阵元的时延,L代表快拍数。
宽带信号带宽为B=fh-fl,将其划分为N个子频带(窄带),各子频带的频率分别为f0,f1,…,fN-1,则第n个子带的接收数据为:
Yn=A(fn,θ)Sn+Wn
n=1,2,…,N
(2)
式(2)中,Sn=[s1s2…sK]T∈K×L,Wn∈M×L。为了简化表示,在下面的章节中A(fn,θ)用An(θ)表示,且An(θ)∈M×K是范德蒙矩阵。第n个子带的导向矢量矩阵表示为:
An(θ)=[a(fn,θ1)a(fn,θ2) …a(fn,θK)]
(3)
其中,第k个信号在第n频带上的导向矢量为:
(4)
式(4)中,d表示阵列阵元间距,c为信号的传播速度。因此,宽带信号的的模型可以写成:
(5)
1.2 非相干子空间方法
基于非相干信号ISM方法是最早出现的宽带DOA估计方法,主要思路是将宽带信号划分为多个子带,对每个子带利用信号子空间或噪声子空间, 求出空间谱或真实信号的根来估计方位角度,最后将各子带所得结果平均作为最终方位估计结果。
根据宽带信号的模型,第n个子带的协方差矩阵为:
(6)
(7)
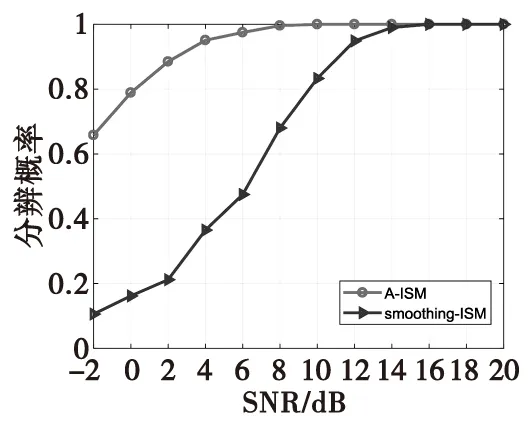
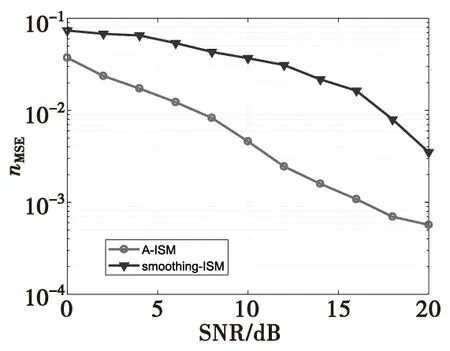
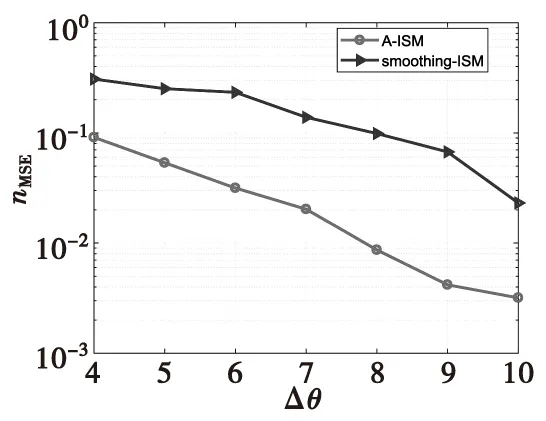
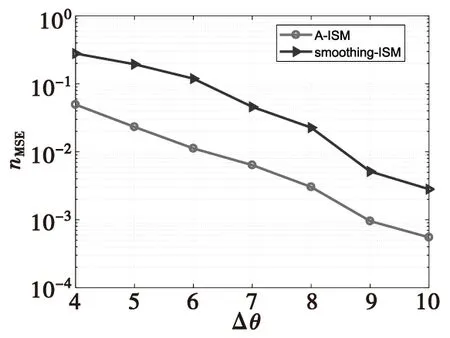
式(7)中,ynl表示第n子带的第l次快拍数据。当L 图2 平滑方法原理图Fig.2 Smoothing method principle structure M元均匀线阵分成相互交错的P个子阵(P=1+M/2),每个子阵的个数为M/2,第n子带平滑后的数据可以表示为: (8) 平滑后协方差矩阵表示为: (9) (10) 其中,特征值λi≫λg,vi和vg分别代表特征值λi和λg对应特征向量,且信号子空间Us和噪声子空间Uw可描述为: (11) 在得到噪声子空间Uw后,将其应用到Root-Music方法中进行DOA估计。首先,Root-Music方法定义为如下一个多项式[13]: (12) 其中 Q(z)=[1z…zM-1]T (13) 由式(12)求出K个接近单位圆的根z1,z2,…,zK。 然后, 根据下式得到第n个子带的DOA估计角度 (14) 随后,对N个子带估计出来的角度求均值,得到最终DOA估计: (15) ISM方法在处理宽带信号时,应用了窄带平均思想,并且要求各子带数据的快拍数必须大于阵元个数,即L>M,否则不能满足子空间类方法对空间协方差矩阵满秩的要求。当数据有限,尤其快拍数L=1时,直接应用传统的ISM方法进行DOA估计时,系统完全不能工作。虽然平滑ISM方法可以估计方位,但是必须以牺牲目标分辨率为代价[14]。针对单快拍下的方位估计,本文提出了基于最小原子范数的宽带非相干子空间DOA估计方法(A-ISM)。该方法可以直接用单快拍数据,通过ANM构造并会恢复出Toeplitz 矩阵进行DOA估计。 在单快拍L=1条件下,第n子带接收的数据可表示为: yn=xn+wn= (16) 式(16)中,yn为M×1的向量,xn∈M×1和wn∈M×1分别表示信号向量和噪声向量。首先考虑无噪声条件,即式(16)中只包含了与角度有关的信号信息,其可写成: yn=xn=An(θ)snn=1,2,…,N (17) 原子核定义为: (18) 式(17)表明,xn是An(θ)的线性组合,因此,xn的原子范数可表示成: (19) 根据文献和式(4)可知,如果信号源是稀疏的,则xn中的sin(θ)就是稀疏的,式(17)就能够进行稀疏原子分解。求解原子范数最小化是一个NP(Non-Deterministic Polynormial)问题,很难直接求解。而原子范数具有半正定规划性质(SDP),采取线性半正定规划方法就能在多项式时间内求解原子范数;同时,由Caratheodory-Toeplitz引理可知,任何半正定Toeplitz矩阵都能进行范德蒙分解[8]。因此,可以将原子范数最小化问题转化为半正定规划问题,其可以描述为[8]: (20) 由式(20)可以解出一个最优的向量un=[un1un2…unM]T,用以构造最优的Toeplitz矩阵[7] (21) 式(20)中的半正定的约束,根据舒尔补(Schur Complement)条件,其可等价于[14]: (22) (23) 实际应用中,噪声总是伴随着信号存在,因此,式(20)中必须考虑对噪声作用进行约束。噪声存在时,ANM的SDP可以重新描述为: (24) 式(24)中,ρ是一个正则化参数,用来调节T(un)的Toeplitz结构与yn中噪声方差。给定了噪声方差σ2,ρ可以根据下式计算[6]: (25) 本章以水下被动探测系统为背景,在单快拍下,利用计算机仿真分别从分辨概率、方位估计归一化均方误差对A-ISM方法和平滑ISM方法的DOA估计性能进行比较分析。 仿真实验中均采用16元均匀线阵,目标源个数K=2,工作频率为3 000~3 100 Hz,子频带个数N=3,快拍数L=1。阵元分布均满足阵元间距为宽带信号最低频率fl对应波长的半波长,水声传播速度c=1 500 m/s。仿真中利用CVX包解决式(20)和式(24)中的SDP问题。 首先,图3比较了目标源位于(30° 36°)时,本文所提的A-ISM方法和平滑ISM方法的分辨概率。本次仿真实验的分辨概率是指在若干次蒙特卡罗实验中,能够正确分辨两个或多个目标的概率。正确分辨需满足以下条件: (26) 式(26)中,B=arcsin(0.44λ/Md) 。由图3可以得出,分辨概率为95%时,A-ISM方法需要的信噪比为4 dB,而平滑ISM方法需要的信噪比为12 dB,A-ISM方法相较平滑ISM方法,信噪比提高了8 dB。 图3 分辨概率与信噪比的关系,L=1,θ=(30° 36°)Fig.3 Probability of resolution versus SNRs,L=1, θ=(30° 36°) 图4中依然假设目标源位于(30° 36°),给出了A-ISM方法和平滑ISM的方位估计性能随信噪比的变化情况,且本节的仿真实验中,方位估计选取归一化均方误差(nMSE)作为衡量方位估计误差的标准,定义为: (27) 图4 归一化均方根误差与信噪比的关系,L=1,θ=(30° 36°)Fig.4 nMSE of DOA versus SNRs,L=1, θ=(30° 36°) 图5和图6比较了两种方法在不同信噪比下,归一化均方误差随着两目标夹角Δθ的变化情况,以此来衡量方法的方位估计性能。从图中可以看出,平滑ISM方法与A-ISM方法的归一化均方误差曲线存在一定的差距,后者估计性能更优。再比较图5和图6,随着信噪比的提高,两种方法的归一化均方误差均有减小,但相较平滑ISM方法,A-ISM方法的归一化均方误差依旧较小,表现出较优的估计性能。 图5 归一化均方误差与的目标夹角关系,SNR=10 dB,L=1Fig.5 nMSE of DOA versus the DOA separation,L=1 图6 归一化均方误差与的目标夹角关系, SNR=15 dB,L=1Fig.6 nMSE of DOA versus the DOA separation,SNR=15dB,L=1 本文提出了基于ANM的宽带非相干子空间DOA估计方法(A-ISM)。该方法通过各子带进行ANM优化处理,恢复出最优的Toeplitz矩阵,该矩阵经过特征分解能准确区分信号子空间和噪声子空间,再结合Root-Music算法,最终得到误差较小的估计角度。该方法不仅解决了单快拍下经典宽带信号DOA估计方法失效问题,而且提高了方位估计性能。仿真结果验证了所提DOA估计方法的正确性和有效性。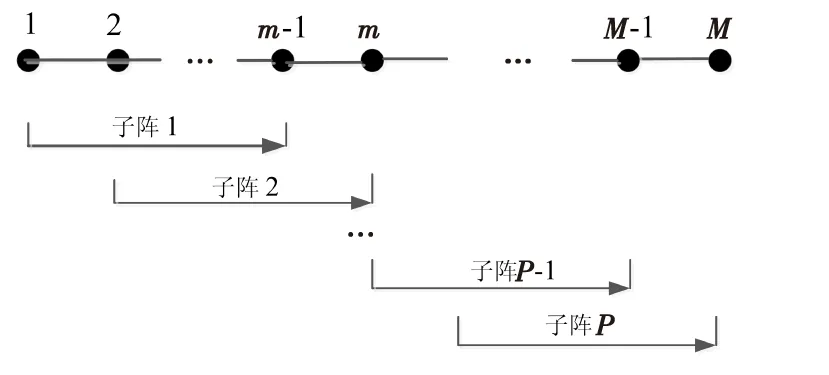
2 基于ANM的宽带非相干子空间方位估计方法
An(θ)sn+wnn=1,2,…,N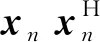
3 仿真与分析
4 结论
